ABSTRACT
Accurate photodissociation cross sections have been obtained for the A1Σ+ ← X1Σ+ electronic transition of HeH+ using ab initio potential curves and dipole transition moments. Partial cross sections have been evaluated for all rotational transitions from the vibrational levels v'' = 0–11 and over the entire accessible wavelength range λλ100–1129. Assuming a Boltzmann distribution of the rovibrational levels of the X1Σ+ state, photodissociation cross sections are presented for temperatures between 500 and 12,000 K. A similar set of calculations was performed for the pure rovibrational photodissociation in the X1Σ+ electronic ground state, but covering photon wavelengths into the far-infrared. Applications of the cross sections to the destruction of HeH+ in the early universe and in UV-irradiated environments such as primordial halos and protoplanetary disks are briefly discussed.
1. INTRODUCTION
Photodissociation is an important mechanism for the destruction of interstellar molecules in diffuse and translucent clouds, in photodissociation regions, in circumstellar disks, in protoplanetary disks, and many other environments with an intense radiation field. HeH+ is believed to be one of the first molecules formed in the early universe (Lepp et al. 2002). Its abundance is kept low due to photodissociation by the cosmic background radiation (CBR) field. Schleicher et al. (2008), however, have suggested that HeH+ can efficiently scatter CBR photons and may generate detectable fluctuations in the cosmic microwave background. Within the Galaxy, Roberge & Dalgarno (1982) discussed the possibility of observing HeH+ in gaseous nebulae. However, to date it has not been detected. Searches in the planetary nebula NGC 7027 have placed upper limits on its abundance through observations of its vibrational (Moorhead et al. 1988) and rotational (Liu et al. 1997; Dinerstein & Geballe 2001) lines. Intensive UV radiation from the central white dwarf may result in efficient photodissociation, providing insight into the low abundance of this molecular ion.
A number of HeH+ photodissociation calculations have been performed over the last three decades (Saha et al. 1978; Flower & Roueff 1979; Roberge & Dalgarno 1982; Basu & Barua 1984; Dumitriu & Saenz 2009; Sodoga et al. 2009). However, they were primarily focused on the A1Σ+ ← X1Σ+ electronic transition from the ground vibrational level. The latter work of Basu & Barua (1984), Dumitriu & Saenz (2009), and Sodoga et al. (2009) also considered transitions to higher electronic states, while Basu & Barua (1984) obtained cross sections from vibrational levels v'' = 0–5, but for a single rotational level. As a consequence, the available HeH+ cross section data set is far from complete, which hinders the ability to accurately model its abundance. In all but the lowest density environments (e.g., diffuse interstellar clouds), excited rovibrational levels of HeH+ are expected to be significantly populated.
To partially address the lack of a comprehensive data set of HeH+ cross sections, we have performed extensive photodissociation calculations for both the X1Σ+ ← X1Σ+
and A1Σ+ ← X1Σ+
transitions using the most accurate available molecular data. Calculations were performed for the full range of 162 bound rovibrational levels (v'', J'') in the ground electronic state using quantum-mechanical techniques. Local thermodynamic equilibrium (LTE) cross sections, which assume a Boltzmann distribution of rovibrational levels, are also computed. In Section 2, an overview of the theory of molecular photodissociation is presented as well as the adopted molecular data. The partial cross sections as well as the LTE photodissociation cross sections for HeH+ are presented in Section 3, while Section 4 briefly highlights the astrophysical importance of the results. Atomic units are used throughout unless stated otherwise.
2. THEORY AND CALCULATION
2.1. Potential Curves and the Dipole Transition Moments
Accurate ab initio calculations of the ground electronic X1Σ+ potential energy including adiabatic corrections have been made by Bishop & Cheung (1979) and are adopted here. For internuclear distances R > 10 a0, a smooth fit to the ab initio potentials has been performed using the average long-range interaction potential,
where αd is the static dipole polarizability of the neutral hydrogen or helium atom. We adopt the values αH = 4.5 and αHe = 1.38309. For R < 0.9 a0, the potential curves have been fit to the short-range interaction potential form Aexp (− BR) + C. For X1Σ+, we obtain a dissociation energy from v'' = 0, J'' = 0 of 1.844 eV using a reduced mass of 1467.3243 a.u. This is very close to the accurate non-Born–Oppenheimer, nonrelativisitic computation of 1.845 eV, which included first-order relativistic corrections, of Stanke et al. (2006) and in agreement with the value of 1.844 eV obtained by Bishop & Cheung (1979).
Ab initio calculations of the excited electronic A1Σ+ state are obtained from Kraemer et al. (1995) and smoothly fit by the same approach. The A1Σ+ potential energy is shifted so that the asymptotic energies as R → ∞ exactly match the difference in experimental H and He ionization potentials. As a consequence, the maximum possible wavelength for a bound–free A1Σ+ ← X1Σ+ transition from the highest-lying rovibrational level in the ground electronic state is less than 1129 Å.
The electric dipole moment function for the ground state X1Σ+ was obtained from the calculations of Juřek et al. (1995) over the range 0.9 < R < 30 a0, while the A1Σ+ ← X1Σ+ electric dipole transition moment function was adopted from Kraemer et al. (1995) over the range of 1.0 < R < 30.0 a0. At short range, both dipole moments were fit to the form AR2 + BR. For R > 30 a0, the ground state dipole function was fit to the form 4R/5, while the transition dipole moment was found to fit well to the form 3.7 × 104/R7.
2.2. The Photodissociation Cross Section
The expression for the cross section for a bound–free transition from initial state i to final state f for an electric dipole transition is given by (e.g., Rau 2002)
where Eph is the photon energy and m the mass of the electron. The continuum differential oscillator strength is defined in the length gauge as
where is the total molecular wave function, the electronic coordinate vector, and the internuclear vector. Inserting Equation (5) into Equation (4) and using the definition of the fine-structure constant, α = e2/ℏc, gives
Taking all quantities in Equation (6) in atomic units, but expressing the cross section in cm2, the numerical value of the pre-factor becomes 2.689 × 10−18. Applying separation of variables for the electronic and nuclear coordinates of Φ, the electric dipole transition moment function is defined as
where integration is taken over all electronic coordinates and is the electronic molecular wave function for fixed R. The rotational photodissociation cross section from initial rovibrational level v''J'' can then be written as
(e.g., Kirby & van Dishoeck 1988), where the Hönl-London factors, , can be expressed for a Σ ← Σ electronic transition as
is the matrix element of the electric dipole transition moment for absorption from the rovibrational level v''J'' in state i to the continuum k'J' in state f, with the integration taken over R. J is the angular momentum of nuclear motion, and g is the degeneracy factor given by
where Λ' and Λ'' are the angular momenta projected along the nuclear axis for the final and initial electronic states, respectively. The continuum wave functions are normalized such that they behave asymptotically as
where is the phase shift. The bound and continuum rovibrational wave functions, and , respectively, are solutions of the radial Schrdinger equation for nuclear motion on the i and f state potential curves, respectively. The wave functions were obtained numerically using the standard Numerov method (Cooley 1961; Blatt 1967; Johnson 1977) with a step size of 0.001 a0 over internuclear distances 0.1 < R < 200 a0.
3. RESULTS AND DISCUSSION
3.1. Partial Cross Sections for the A←X Electronic Photodissociation
A sampling of the partial cross sections for the A1Σ+ ← X1Σ+ transition is presented in Figures 1–4 as a function of the photon wavelength λ. In Figure 1, the partial cross sections for photodissociation of HeH+ from the rovibrational level v'' = 0, J'' = 1 are presented and compared to previous calculations. The current calculations are shown to be in excellent agreement with the earlier results of Roberge & Dalgarno (1982) and Basu & Barua (1984), while the cross section peak obtained by Saha et al. (1978) is seen to be shifted to longer wavelengths. The more recent calculations of Dumitriu & Saenz (2009) and Sodoga et al. (2009) include contributions from transitions to higher electronic states of HeH+, which are not considered in the current work. In most astrophysical environments, there are few photons at such short wavelengths so that our neglect of the higher electronic transitions is reasonable. Nevertheless, there is excellent agreement between the current calculations and those of Dumitriu & Saenz (2009) for λ > 440 Å and good agreement with the results of Sodoga et al. (2009), though their A ← X peak is shifted to shorter wavelengths.
Figure 1. Partial photodissociation cross sections as a function of wavelength λ for the A1Σ+ ← X1Σ+ transition of HeH+ from the vibrational level v'' = 0 (with J'' = 1). Solid line, current calculation; dotted line, Saha et al. (1978); dashed line, Basu & Barua (1984); long dashed line, Roberge & Dalgarno (1982); dot-dash line, Dumitriu & Saenz (2009); dash-dot-dash line, Sodoga et al. (2009). Note the latter two calculations also include contributions from higher excited electronic states which give contributions for λ ≲ 450 Å.
Download figure:
Standard image High-resolution imageFigure 2. Same as Figure 1, but for v'' = 8, J'' = 1. Solid line, current calculation; dashed line, Saha et al. (1978).
Download figure:
Standard image High-resolution imageFigure 3. Partial photodissociation cross sections for the A1Σ+ ← X1Σ+ transition of HeH+ for v'' = 10 and all J''.
Download figure:
Standard image High-resolution imageFigure 4. Same as Figure 3, but for J'' = 0 and select v''.
Download figure:
Standard image High-resolution imageExperimental studies of molecular photodissociation is largely an unexplored area of research and we are aware of only one measurement for HeH+ performed at the free-electron laser in Hamburg by Pedersen et al. (2007). They obtained a cross section of (1.4 ± 0.7) × 10−18 cm2, but for fragmentation into H+ and He(n ⩾ 2) at 320 Å. While the Dumitriu & Saenz (2009) and Sodoga et al. (2009) cross sections shown in Figure 1 also include the H(n ⩾ 2) + He+ fragmentation channels, Sodoga et al. (2009) find good agreement with the measurements when only the H+ + He channels are considered. Indirectly, this suggests that the current calculations at somewhat longer wavelengths are consistent with experiment.
Figure 2 shows our results for the partial cross sections from the vibrational level v'' = 8, J'' = 1 in comparison to the earlier calculations of Saha et al. (1978). As for the v'' = 0, J'' = 1 case, the Saha et al. (1978) cross sections are shifted to longer wavelengths. Given the ionization potentials of H and He and the binding energy of the v'' = 8, J'' = 1 level, the photodissociation threshold is 1123 Å, which is consistent with the current results. Further, the current v'' = 8, J'' = 1 binding energy is in excellent agreement with the value obtained by Zygelman et al. (1998).
Additional cross sections are presented in Figure 3 for v'' = 10 and all bound J'' and in Figure 4 for v'' = 0–11, for J'' = 0. While not shown, good agreement is found with the A ← X, v'' = 1–5, J'' = 1 cross sections of Basu & Barua (1984). Good agreement is also found with the results of Sodoga et al. (2009) for v'' = 0, J'' = 10 and v'' = 1, J'' = 0, though their cross sections are again somewhat shifted to shorter wavelengths.
We note that our cross sections include results from rovibrational levels which are very near the dissociation limit for which there is, as yet, no experimental evidence in some cases. These are typically the last rotational level in each vibrational manifold including v'', J'' = (0, 23), (1, 21), (2, 20), (3, 18), (4, 16), (5, 14), (6, 12), (7, 10), (8, 7), and (9, 5), but also all v'' = 10 and 11 levels. All but v'', J'' = (0, 23) were obtained by Zygelman et al. (1998) using a similar approach, while the non-Born–Oppenheimer method of Stanke et al. (2006) predicts that v'', J'' = (11, 0) is bound. However, transitions involving the v'', J'' = (0, 23), (1, 21), and (2, 20) levels have been detected in a number of experiments (e.g., Liu & Davies 1997).
3.2. LTE Cross Sections for A←X Photodissociation
The total quantum-mechanical cross section for photodissociation as a function of both temperature T and wavelength in LTE is given by (e.g., Argyros 1974)
where a Boltzmann population distribution is assumed for the rovibrational levels in the electronic ground state, is the total vibrational–rotational statistical weight, Eg is the binding energy of the lowest rovibrational level, kb is the Boltzmann constant, and is the partition function given by
In both Equations (12) and (13), Eg and the binding energies are taken as positive quantities. We obtain partition functions in excellent agreement with those computed by Engel et al. (2005) for T = 1–4000 K, but our values are somewhat smaller for higher temperatures.
Figure 5 displays LTE cross sections for the A1Σ+ ← X1Σ+ photodissociation transition as a function of the wavelength for temperatures between 500 and 12,000 K as given by Equation (12). The threshold wavelength at 1129 Å corresponds to the asymptotic energy gap between the A1Σ+ and X1Σ+ electronic states. As the temperature increases, the cross section for wavelengths between ∼800 and 1129 Å increases dramatically, though the peak cross section near 500 Å decreases. In particular, for T > 3000 K, the cross section longward of the hydrogen Lyman limit becomes significant.
Figure 5. Total HeH+ A1Σ+ ← X1Σ+ LTE photodissociation cross section for temperatures from 500 to 12,000 K. The v'' = 0, J'' = 0 partial cross section is also plotted for comparison.
Download figure:
Standard image High-resolution image3.3. The Partial Cross Sections for X←X Rovibrational Photodissociation
For irradiated environments with photon wavelengths much greater than the Lyman limit, photodissociation via pure rovibrational transitions may be dominant although the cross sections are typically small. For example, in Figure 6, the partial cross section for rovibrational photodissociation in the X1Σ+ electronic state for v'' = 8, J'' = 1 is presented and comparison is made with the earlier calculations of Saha et al. (1978). As for the A←X case, there is a significant shift in the threshold wavelength likely due to an inaccurate binding energy calculation in the earlier work. Additional examples of rovibrational photodissociation for the X1Σ+ ← X1Σ+ transition are given in Figures 7 and 8. Figure 7 displays photodissociation from the ground rovibrational level (v'' = 0, J'' = 0) which has a threshold of 6732 Å and a peak cross section magnitude that is ∼107 times smaller than for the A1Σ+ ← X1Σ+ electronic transition. Figure 7 also displays cross sections from v'' = 0 and a selection of J''. Orbiting resonances due to quasi-bound levels are evident for J'' ≳ 5 near thresholds. Figure 8 displays similar results, but for J'' = 0 and a selection of v''. We are unaware of other previous rovibrational photodissociation calculations for HeH+.
Figure 6. Partial photodissociation cross section of v'' = 8, J'' = 1 for the X1Σ+ ← X1Σ+ rovibrational transition. Solid line, current calculation; dashed line, Saha et al. (1978).
Download figure:
Standard image High-resolution imageFigure 7. Partial photodissociation cross sections for the X1Σ+ ← X1Σ+ rovibrational transition for v'' = 0 and select J''.
Download figure:
Standard image High-resolution imageFigure 8. Same as Figure 7, but for J'' = 0 and select v''.
Download figure:
Standard image High-resolution image3.4. LTE Cross Sections for X←X Rovibrational Photodissociation
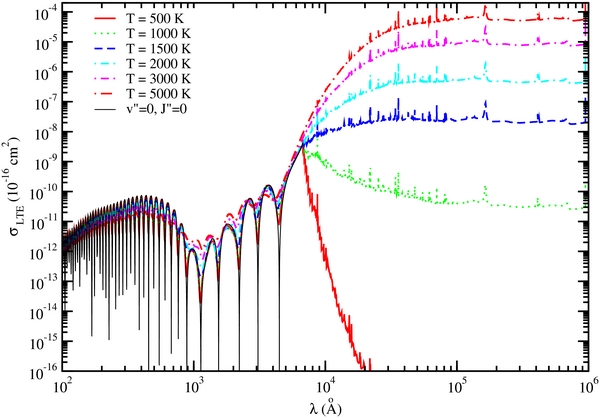
Assuming a Boltzmann population distribution of rovibrational levels in the ground electronic state, LTE cross sections are computed for gas temperatures between 500 and 5000 K. Figure 9 shows LTE cross sections for the X1Σ+ ← X1Σ+ photodissociation of HeH+ as a function of the wavelength. For T less than ∼1000 K, the LTE cross section peaks at a wavelength corresponding to the v'' = 0, J'' = 0 threshold. Photons in this wavelength range are primarily responsible for photodestruction of HeH+. For higher temperatures, the population in highly excited v'', J'' levels contributes substantially to the cross section increasing its value at large wavelength.
Figure 9. Total HeH+ X1Σ+ ← X1Σ+ LTE photodissociation cross section for temperatures from 500 to 5000 K. The v'' = 0, J'' = 0 partial cross section is also plotted for comparison.
Download figure:
Standard image High-resolution image4. ASTROPHYSICAL APPLICATIONS
The possible presence of HeH+ in astrophysical environments was probably first discussed by Dabrowski & Herzberg (1978), while early models of its abundance and emission lines in gaseous nebulae were performed by Black (1978) and Flower & Roueff (1979). Later, Roberge & Dalgarno (1982) gave a comprehensive discussion of the mechanisms for the formation and destruction of HeH+ in astrophysical plasmas. Over the subsequent three decades, the role of HeH+ has been considered in a variety of environments. Zygelman et al. (1998) and Stancil & Dalgarno (1998) discussed the formation of HeH+ in supernova ejecta, planetary nebulae, high-z Lyα clouds, and broad-line clouds. Searches for its rotational and vibrational emission features, focusing on planetary nebula NGC 7027, have so far been unsuccessful. However, Miller et al. (1992) proposed a tentative identification in the ejecta of supernova 1987A, but this has yet to be confirmed. Here, we discuss three environments in which HeH+ is expected to have a significant abundance and the possible impact of the current photodissociation cross sections including the early universe, population III objects, and protoplanetary disks. We do not provide photodissociation rates as they are sensitive to the properties of the local radiation field including its shape, intensity, and attenuation via the local dust and gas. Instead, we provide cross sections to facilitate calculation of local photorates.
In the recombination era of the early universe, radiation from the CBR field can efficiently destroy HeH+ through the X1Σ+ ← X1Σ+ rovibrational transition until a redshift of z ∼ 300 (Galli & Palla 1998; Stancil et al. 1998; Lepp et al. 2002; Schleicher et al. 2008). Early universe chemical models typically obtain the destruction rate via detail balance from the radiative association rate coefficient. Given that HeH+ has a dipole moment, the CBR field will likely thermalize the rovibrational populations. The current results, shown in Figure 9, could be used to improve such calculations by directly obtaining the photodissociation rate due to the CBR field. For illustrative purposes, both the X←X and A←X LTE cross sections for a gas temperature of 1000 K are plotted in Figure 10 and compared to blackbody radiation curves for a number of radiation temperatures Tr. For z between ∼1000 and 300 (Tr ∼ 3000 and 1000 K), the X←X transition dominates the photodissociation, but for higher z the A←X transition will become important (see also Figure 5), though it is neglected in current models. For 1000 ≲ z ≲ 3000, models predict a plateau in the HeH+ abundance (Zygelman et al. 1998; Stancil et al. 1998; Schleicher et al. 2008). While the abundance at this redshift is small, it would likely be further suppressed due to photodissociation via the A←X transition.
Figure 10. Total HeH+ LTE photodissociation cross section at 1000 K for both the X1Σ+ ← X1Σ+ and A1Σ+ ← X1Σ+ transitions. Blackbody radiation curves (dotted lines) for various radiation temperatures are plotted for comparison.
Download figure:
Standard image High-resolution imageIn Miyake et al. (2010), we considered the photodetachment of H− due to far-UV (FUV) sources prior to the reionization epoch including population III (Pop III) stars and the high-z intergalactic medium (IGM) radiation field. Once a Pop III star is formed, the HeH+ present in its primordial halo, which consists of baryonic and dark matter, will be exposed to an intense FUV stellar radiation field. As Pop III stars are expected to be massive, they will emit essentially blackbody radiation with effective temperatures Teff between ∼30,000 and 107 K (Schaerer 2002). Figure 10 illustrates that Pop III stellar radiation will photodissociate HeH+ through both the A1Σ+ ← X1Σ+ and X1Σ+ ← X1Σ+ transitions with the A←X contribution increasing with Teff. Roberge & Dalgarno (1982) computed A←X photodissociation rates for 20,000 ⩽ Teff ⩽ 500,000 K for complete blackbodies and with a 24.6 eV cutoff accounting for He i continuum opacity. However, the Pop III FUV radiation will carve out a surrounding H ii region resulting in a 13.6 eV cutoff at the Lyman limit (reducing the rate), but the densities in the molecular region may be high enough for the HeH+ level populations to approach a thermal distribution. The latter effect is likely to increase the rate, as suggested by Figures 5 and 10, since Roberge & Dalgarno (1982) only considered photodissociation from v'' = 0, J'' = 1. Further, the B←X, C←X, and higher electronic transitions will play little role due to Lyman limit or He i cutoffs. On the other hand, the high-redshift IGM radiation field is expected to have a Lyman limit cutoff, to be modulated by H i resonant absorption, and to behave as a power law at longer wavelengths (e.g., Miyake et al. 2010), so that HeH+ present in the outer molecular regions of primordial halos exposed to the IGM field would be photodissociated primarily through the X1Σ+ ← X1Σ+ transition.
Photoprocesses are known to have a significant influence on molecular gas in protoplanetary disks as they are exposed to intense UV radiation from the young star (e.g., van Dishoeck et al. 2008) and the accretion disk (France et al. 2011) and to infrared radiation from dust grains (e.g., Gorti & Hollenbach 2004). As pointed out by van Dishoeck et al. (2008), the environment of a protoplanetary disk is likely to be vastly different from average interstellar conditions including (1) dust grains with different sizes and properties, (2) varying spectral shapes of the incident UV radiation, (3) higher intensity radiation, and other factors. Therefore, pre-computed photorates cannot be readily applied. The gas temperature is typically ∼50 K in the mid-plane, but increases with height and toward the star, reaching a few 1000 K in the inner disk. The dust temperature decreases from ∼400 K in the inner disk to ∼100 K in the mid-plane of the outer disk (Gorti & Hollenbach 2004). Effective stellar temperatures range from 4000 K for a T Tauri star to ∼30,000 K (van Dishoeck et al. 2008), while the accretion shock radiation is expected to approach the Lyman limit with intensities 105–107 that of the standard interstellar radiation field (France et al. 2011). For the high densities (104–107 cm−3) in the disk, the HeH+ rovibrational populations would be expected to be thermalized so that LTE photodissociation cross sections would be appropriate. While van Dishoeck et al. (2008) mention that HeH+ cannot be photodissociated, Figure 10 suggests that photodissociation can occur due to dust and cooler stellar radiation through the X←X transition. Hotter stars, and in particular the intense accretion radiation, may dominate the photodissociation rate through the A←X transition shortward of 1129 Å. However, intense Lyα, from T Tauri stars, which may contribute to the photodissociation of other molecular, will have a negligible effect for HeH+.
5. CONCLUSIONS
Using ab initio potentials and dipole moment functions, accurate cross section calculations have been performed for the photodissociation of HeH+ through the A1Σ+ ← X1Σ+ and X1Σ+ ← X1Σ+ transitions. The partial cross sections have been evaluated for all the rotational transitions from the vibrational levels v'' = 0–11 of the X1Σ+ electronic state. LTE cross sections are also calculated for temperatures between 500 and 12,000 K. The resulting cross sections are applicable to the destruction of HeH+ in the early universe and in UV irradiated molecular regions including primordial halos, photodissociation regions, and protoplanetary disks. To facilitate the calculation of local photorates for particular astrophysical environments, all photodissociation cross section data can be obtained from the UGA Molecular Opacity Project Web site (http://www.physast.uga.edu/ugamop/).
This work was supported by NSF Grant AST-0607733 and HST-AR-11776.01-A which was provided by NASA through a grant from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555.