A NUMERICAL STUDY OF DIFFUSIVE COSMIC-RAY TRANSPORT WITH ADIABATIC FOCUSING

The Fokker–Planck equation for a cosmic-ray distribution function, which incorporates the effects of pitch-angle scattering and adiabatic focusing, is given by

$$\begin{equation} \frac{\partial f_0}{\partial t} + \mu v \frac{\partial f_0}{\partial z} + \frac{v}{2L} (1 - \mu ^2) \frac{\partial f_0}{\partial \mu } = \frac{\partial }{\partial \mu } \left(D_{\mu \mu } \frac{\partial f_0}{\partial \mu } \right) \end{equation} \tag{ 1 }$$

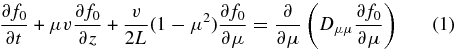
(e.g., Roelof 1969; Earl 1981). Here f₀ is the distribution function of energetic particles (gyrotropic phase-space density), t is time, μ is the cosine of the particle pitch angle, v is the particle speed, z is the distance along the mean magnetic field B₀, L = −B₀/(∂B₀/∂z) is the adiabatic focusing length, and D_μμ is the Fokker–Planck coefficient for pitch-angle scattering. For simplicity, momentum diffusion is neglected. In practice, momentum diffusion can be neglected for the transport of solar energetic particles in interplanetary space (Artmann et al. 2011).

As a concrete illustration, throughout this paper we assume a constant focusing length, L = const, and isotropic pitch-angle scattering:

$$\begin{equation} D_{\mu \mu } = D_0 (1 - \mu ^2), \end{equation} \tag{ 2 }$$

where D₀ = const. An exact steady solution of Equation (1) is then given by

$$\begin{equation} f_0(\mu , z) = \mbox{const} \, \exp \left(\frac{\mu v}{2 D_0 L} - \frac{z}{L} \right) \end{equation} \tag{ 3 }$$

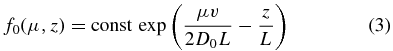
(Kunstmann 1979; Roelof 1969). Physical regimes leading to isotropic pitch-angle scattering have been analyzed by Shalchi et al. (2009).

Numerical studies of particle transport often employ the fact that a system of stochastic differential equations contains the same information about the evolution of the particle distribution as the Fokker–Planck equation (e.g., Fichtner et al. 1996; Zhang 1999; Pei et al. 2010; Dröge et al. 2010; Strauss et al. 2011). In particular, standard application of the Itô calculus (e.g., Litvinenko 2012a) shows that Equation (1) in the case of isotropic pitch-angle scattering and L = const is completely equivalent to the system

$$\begin{equation} dz = \mu v dt, \end{equation} \tag{ 4 }$$

$$\begin{equation} d \mu = \left[ \frac{v}{2L} (1 - \mu ^2) - 2 D_0 \mu \right] dt + \sqrt{2 D_0 (1 - \mu ^2)} dW, \end{equation} \tag{ 5 }$$

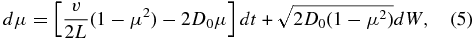
where W(t) represents a Wiener process with zero mean and variance t (Gardiner 2009).

If the time-dependent angular distribution of energetic particles remains close to that of the exact Equation (3), integration of a perturbed Fokker–Planck equation over μ leads to the diffusion approximation for the evolution of the particle density. As shown by Beeck & Wibberenz (1986), the resulting equation for the isotropic linear density

$$\begin{equation} F(z, t) = \frac{1}{2} \int _{-1}^{1} e^{z/L} f_0 d \mu \end{equation} \tag{ 6 }$$

is as follows:

$$\begin{equation} \frac{\partial F}{\partial t} + u \frac{\partial F}{\partial z} = \kappa _{\Vert } \frac{\partial ^2 F}{\partial z^2}. \end{equation} \tag{ 7 }$$

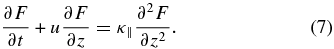
In Equation (7),

$$\begin{equation} u = \frac{\kappa _{\Vert }}{L} \end{equation} \tag{ 8 }$$

is the coherent speed, and κ_|| is the parallel diffusion coefficient. Because this mode of particle transport comprises both coherent streaming and diffusion, Earl (1981) called it pseudo-diffusion.

Note for clarity that the sign of the convective term in Equation (7) is different from that in Equation (17) in Beeck & Wibberenz (1986). This is because Beeck & Wibberenz (1986) used the phase-space density, whereas Equation (7) is written for the linear density, defined as the number of particles per line of force per unit distance parallel to B₀. The two descriptions are mathematically equivalent (Earl 1981). Because the mean magnetic field is proportional to exp (− z/L), the cross-sectional area of a flux tube scales as exp (z/L), and so the particle conservation is conveniently expressed as N(t) = 2∫Fdz = const.

Clearly κ_|| is the key parameter controlling the particle transport. Beeck & Wibberenz (1986) derived an expression for κ_|| in terms of the pitch-angle scattering rate D_μμ and the focusing length L. In the limit L → ∞, the expression for κ_|| reduces to that in Hasselmann & Wibberenz (1970). When scattering is isotropic, Equation (14) in Beeck & Wibberenz (1986) yields

$$\begin{equation} \kappa _{\Vert ,{\rm BW}} = \lambda _0 v \left(\frac{\coth \xi }{\xi } - \frac{1}{\xi ^2} \right), \end{equation} \tag{ 9 }$$

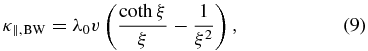
where ξ = λ₀/L is the focusing parameter, and

$$\begin{equation} \lambda _0 = \frac{3v}{8} \int _{-1}^{1} \frac{(1 - \mu ^2)^2}{D_{\mu \mu }} d \mu = \frac{v}{2 D_0} \end{equation} \tag{ 10 }$$

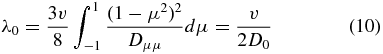
is the scattering mean free path in the absence of focusing (e.g., Equation (3) in Beeck & Wibberenz (1986)). By contrast, a recent calculation by Shalchi (2011) leads to a different expression for κ_|| = λv/3. Equation (33) for the scattering length λ in Shalchi (2011) yields

$$\begin{equation} \kappa _{\Vert ,S} = \lambda _0 v\left(\frac{1}{\xi ^2} - \frac{\tanh \xi }{\xi ^3} \right). \end{equation} \tag{ 11 }$$

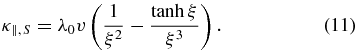
Clearly the two expressions for the parallel diffusion coefficient are contradictory, except in the limit of no focusing, ξ → 0, when both expressions yield

$$\begin{equation} \kappa _{\Vert ,0} = \frac{1}{3} \lambda _0 v = \frac{v^2}{6D_0}. \end{equation} \tag{ 12 }$$

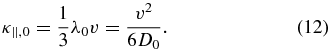
Shalchi (2011) did not discuss the earlier calculations by Earl (1981) and Beeck & Wibberenz (1986).

Since the diffusion approximation is the standard approximation for studying the cosmic-ray transport (e.g., Kóta et al. 1982; Schlickeiser & Shalchi 2008; Artmann et al. 2011), the discrepancy between κ_{||, BW} and κ_{||, S} is troubling. To evaluate the validity of the conflicting theoretical results, below we present numerical solutions of the Fokker–Planck equation. We compute an evolving spatial density profile F(z, t) and compare the numerical results with the theoretical predictions of the diffusion approximation. We also investigate the predicted and computed dependencies of the solutions on the focusing parameter ξ.

The validity of the diffusion approximation usually requires that the focusing be sufficiently weak, say ξ < 1. Both expressions for the parallel diffusion coefficient, however, are formally valid for an arbitrary ξ. In the next section, we determine the dependence of our numerical results on the focusing strength in a sufficiently wide range 0 ⩽ ξ ⩽ 2, which simplifies the comparison of the numerical and analytical results.

We solved the Fokker–Planck Equation (1) for a range of focusing strengths and time intervals by integrating the stochastic differential Equations (4) and (5). We introduced dimensionless variables by measuring distances in units of the mean free path λ₀ = v/2D₀, speeds in units of the constant particle speed v, and times in units of λ₀/v = 1/2D₀. The dimensionless stochastic equations are as follows:

$$\begin{equation} dz = \mu dt, \end{equation} \tag{ 13 }$$

$$\begin{equation} d \mu = \left[ \frac{1}{2} \xi (1 - \mu ^2) - \mu \right] dt + \sqrt{1 - \mu ^2} dW, \end{equation} \tag{ 14 }$$

where we used the identity W(a²t) = aW(t). The only parameter of the simulation is the dimensionless focusing strength ξ that we vary in the range 0 ⩽ ξ ⩽ 2. The parallel diffusion coefficients are normalized by λ₀v = v²/2D₀, which gives the dimensionless κ_{||, 0} = 1/3 in a uniform mean magnetic field (ξ = 0).

The stochastic equations are more convenient to work with than the original Fokker–Planck equation. We solve Equations (13) and (14) using the Milstein approximation scheme:

$$\begin{equation} z_{t+\Delta t} = z_t + \mu _t \Delta t, \end{equation} \tag{ 15 }$$

$$\begin{eqnarray} \mu _{t+\Delta t} &=& \mu _t + \left[ \frac{1}{2}\xi \left(1-\mu _{t}^{2} \right)-\mu _t \right] \Delta t + \sqrt{\Delta t \left(1-\mu _{t}^{2} \right)} \, \epsilon _t \nonumber\\ && - \frac{1}{2}\mu _t \Delta t \left(\epsilon _{t}^{2}-1 \right), \end{eqnarray} \tag{ 16 }$$

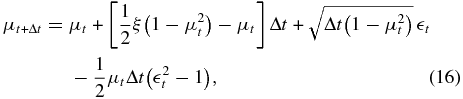
where _t is a normal random variable with mean zero and variance unity (Kloeden & Platen 1999). Particles are reflected at μ = ±1 to conserve probability at these boundaries. Most conveniently, particle distribution moments are obtained simply by evaluating the appropriate sample moments from the particle simulations.

The numerical results described in this section correspond to a delta-functional initial distribution in position and isotropic pitch-angle distribution, f₀(μ, z, t = 0) = δ(z). (A normalization constant is not significant since the original differential equation is linear.) We also verified that an anisotropic distribution at t = 0 does not alter the numerical results after a brief transitional period.

We calculated time-dependent density profiles F(z, t) by binning the particles with any pitch-angle cosine μ in a given position interval between z and z + Δz, and we compared the resulting density profiles with the theoretical predictions of the diffusion approximation. Specifically, the solution of Equation (7) with a delta-functional initial condition is given by a moving pulse

$$\begin{equation} F(z, t) = \frac{1}{(4 \pi \kappa _{\Vert } t)^{1/2}} \exp \left[ - \frac{(z-ut)^2}{4 \kappa _{\Vert } t} \right], \end{equation} \tag{ 17 }$$

where the parameters u and κ_|| are defined by Equation (8), and either Equation (9) or Equation (11) in dimensionless form.

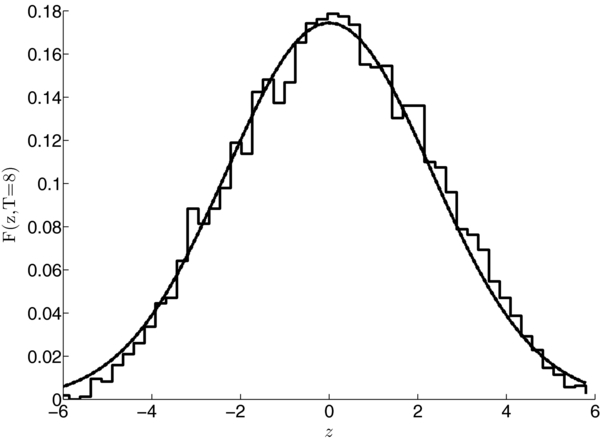
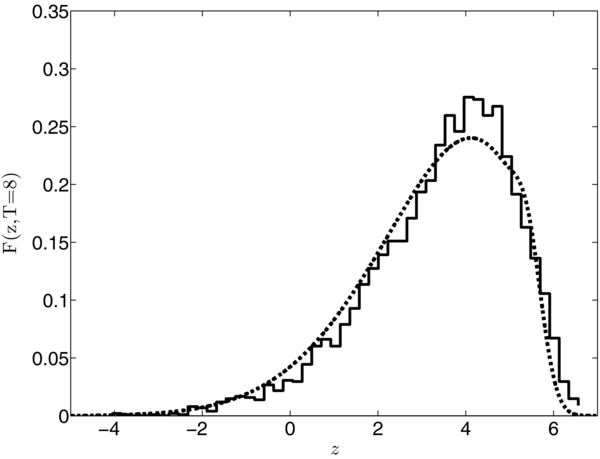
The transport coefficients calculated by Beeck & Wibberenz (1986) and by Shalchi (2011) coincide in the case of no focusing, when ξ = 0, κ_{||, 0} = 1/3 and u = 0. Figure 1 shows an excellent agreement between the analytical solution of Equation (17) (black curve) and numerical results (histogram) in the case of no focusing at time t = 8. The numerical results are obtained by solving Equations (15) and (16) with 10⁶ particles and time step Δt = 0.004. The close agreement reinforces the results of the earlier numerical studies of diffusive particle transport, performed by Kóta et al. (1982). We also confirmed that the diffusion approximation remains accurate at t = 15.

Zoom In Zoom Out Reset image size

Figure 2 shows the snapshot of a moving density pulse in the case of strong focusing, ξ = 1.5. The numerical results (histogram) are obtained by solving Equations (15) and (16) with 10⁶ particles and time step Δt = 0.004. Interesting differences among the analytical and numerical profiles emerge. The diffusive transport model of Beeck & Wibberenz (1986) (solid curve) clearly predicts the location z = ut of the peak of the pulse better than the model of Shalchi (2011; dashed curve). The model of Beeck & Wibberenz (1986) also reproduces the density profile for z < ut quite well, whereas the profile based on the model of Shalchi (2011) cannot reproduce the numerically obtained profile, even if the theoretical profile is shifted to the right to match the density peak. We confirmed that the results are similar for other values of ξ > 0 at t = 8, as well as at t = 15.

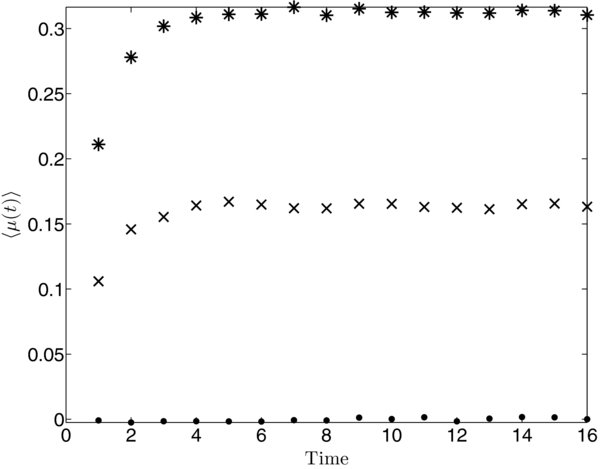
Zoom In Zoom Out Reset image size

Figure 3 presents the dimensionless mean speed, computed from the averaged Equation (13), d〈z〉/dt = 〈μ〉, against time. For each value of time we approximate 〈μ〉 using the mean pitch-angle cosine of 10⁶ particles. The dimensionless mean speed 〈μ〉 is plotted for ξ = 0 (points), ξ = 0.5 (crosses), and ξ = 1 (asterisks). In all cases, a constant value of 〈μ〉 is reached after a transitional period of a few scattering times.

Zoom In Zoom Out Reset image size

The transitional period corresponds to the relaxation of the angular part of the distribution function f₀(μ, z, t) to a steady distribution. Figure 4 presents the angular distribution computed using 10⁶ particle simulations with ξ = 0.5. The initial uniform distribution is given (black histogram), together with the distribution at t = 2 (blue histogram) and the distribution at t = 6 (red histogram). The black curve is an exact steady analytical solution for the angular distribution, h(μ) = Aexp (ξμ) (Roelof 1969), where the normalization constant is A = ξ/2sinh (ξ). As emphasized by Litvinenko (2012b), rapid relaxation to the steady angular distribution h(μ) is a key requirement in the derivation of the diffusion approximation.

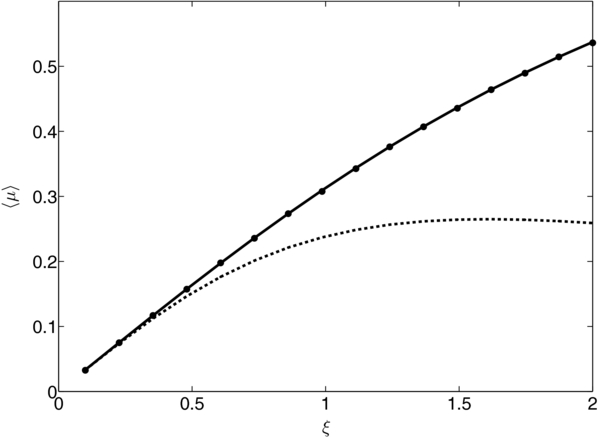
Zoom In Zoom Out Reset image size

The mean particle speed can be used as a test of the accuracy of the diffusion approximation. Figure 5 shows the dependence of the dimensionless mean speed, computed from the averaged Equation (13), on the focusing parameter ξ. For each value of ξ, we compute d〈z〉/dt = 〈μ〉 using the mean pitch-angle cosine of 10⁶ particles at a terminal time T (black points). To allow relaxation of the angular distribution to a steady distribution, we choose a terminal time T, for each individual particle, to be uniformly distributed between 5 < T < 15. Simulations use a time step Δt = T/2000. The solid curve is the theoretical coherent speed u = ξκ_{||, BW} due to Beeck & Wibberenz (1986), and the dashed curve is the coherent speed u = ξκ_{||, S} due to Shalchi (2011). Figure 5 confirms that the diffusion model of Beeck & Wibberenz (1986) yields the correct value of the mean speed for the range of focusing strengths used in the simulations.

Zoom In Zoom Out Reset image size

Finally, we note that the computed density profile ahead of the peak at z = ut in Figure 2 is particularly interesting. Since all particles have finite speed v, the density F(z, t) must vanish for z > vt (recall that the particle speed v = 1 in our dimensionless units). Hence the computed profile has a sharp front propagating to the right, and the particles pile up in the range ut < z < vt. Obviously these effects cannot be described by the diffusion approximation that has infinite propagation speed, and so the asymmetry of the density profile about the peak indicates the breakdown of the diffusion approximation. We return to this point in Section 3.4 below.

In order to better understand the reason for the disagreement between our numerical results and the analytical predictions of Shalchi (2011), we now investigate the variance of the particle distribution, var(z) = 〈z²〉 − 〈z〉². On differentiating this with respect to time and using the averaged Equation (13), we get

$$\begin{equation} \frac{1}{2} \frac{d}{dt} \mbox{var}(z) = \langle \mu z \rangle - \langle \mu \rangle \langle z \rangle. \end{equation} \tag{ 18 }$$

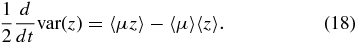
We use the right-hand side of this equation to compute the rate of change of the variance for the evolving particle distribution.

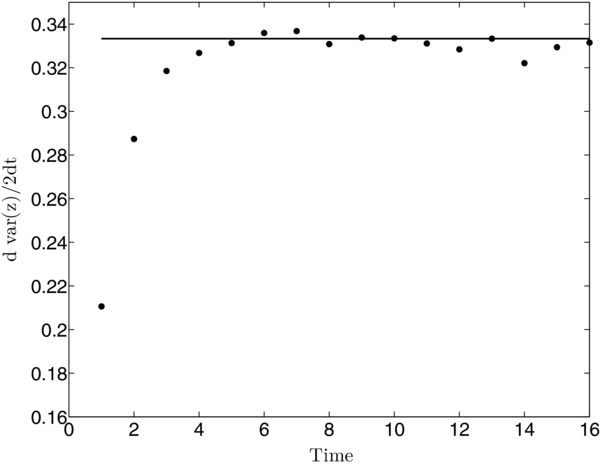
Consider first the limit of no focusing, ξ = 0. Figure 6 shows that after a brief transitional period when the particle motion is non-diffusive, dvar(z)/2dt = κ_{||, 0} = 1/3, and so the variance is a linear function of time. This is a well-known result of the diffusion approximation (Kóta et al. 1982). As described above, the transitional period of a few scattering times corresponds to the relaxation of the angular distribution to a steady anisotropic distribution.

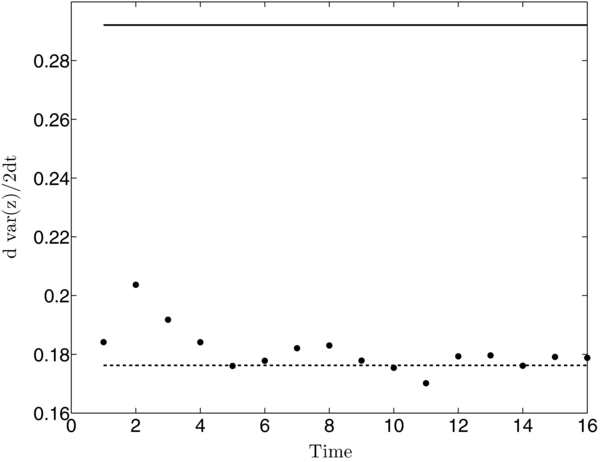
Zoom In Zoom Out Reset image size

Figure 7 shows the temporal behavior of dvar(z)/2dt in the case of strong focusing, ξ = 1.5. The solid line is the theoretical prediction κ_{||, BW} = 0.29 due to Beeck & Wibberenz (1986), and the dashed line is the theoretical prediction κ_{||, S} = 0.18 due to Shalchi (2011). The particle motion is initially non-diffusive, and then the variance grows linearly with time. It is clear from Figure 7 that with a high degree of accuracy dvar(z)/2dt = κ_{||, S} after a transitional period.

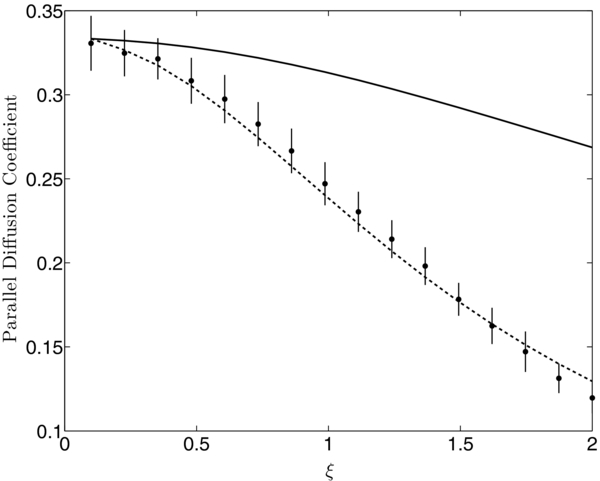
Zoom In Zoom Out Reset image size

Figure 8 compares the two analytical expressions for the parallel diffusion coefficient κ_|| with the computed dvar(z)/2dt for 0 < ξ ⩽ 2 (standard errors are also shown). As in the calculation of the mean speed, we used the terminal time T, uniformly distributed between 5 < T < 15, and a time step Δt = T/2000. The solid and dashed curves are the dimensionless parallel diffusion coefficients predicted by Beeck & Wibberenz (1986) and Shalchi (2011), respectively. This figure confirms that dvar(z)/2dt = κ_{||, S} for the complete range of focusing strengths (0 ⩽ ξ ⩽ 2) for which we computed the particle distributions.

Zoom In Zoom Out Reset image size

Our numerical results indicate that what Shalchi (2011) calculated, at least in the case of isotropic scattering, is

$$\begin{equation} \kappa _{\Vert ,S} = \frac{1}{2} \frac{d}{dt} \mbox{var}(z). \end{equation} \tag{ 19 }$$

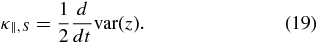
This equation could serve as a correct definition of the diffusion coefficient if the diffusion approximation were sufficiently accurate for all z. As we demonstrated, however, the approximation breaks down ahead of a propagating density pulse, as a consequence of a finite particle speed. We conclude that the analysis of Beeck & Wibberenz (1986) describes correctly the location of the density maximum at z = ut and the dispersion of the cosmic-ray particles for z ⩽ ut, whereas the model of Shalchi (2011), while leading to a formally correct integral characteristic of the distribution, is physically less useful because it essentially assumes the diffusion approximation to be perfectly valid everywhere. Neither model is reliable ahead of the density pulse for z > ut where the diffusion approximation breaks down.

Interestingly, the diffusion approximation does appear to be valid for any z in the case of a uniform mean magnetic field (see Figure 1). The reason for this appears to be related to the fact that the coherent speed u vanishes when adiabatic focusing is absent. Very few particles are predicted to diffuse far from the origin in this case, which is why the resulting error is small. By contrast, strong focusing leads to a large value of the coherent speed, and as illustrated by Equation (17), the diffusion approximation predicts a much greater number of particles even far ahead of a propagating density pulse. Since this is physically impossible, in reality the particles pile up directly ahead of the density peak, creating a sharp propagating front (Figure 2).

The diffusion approximation for particle density is derived by separating the particle distribution function into the isotropic and anisotropic parts and by finding an approximate expression for the anisotropic part g = f₀ − F₀ (Beeck & Wibberenz 1986). When perturbation methods are used to get a more accurate expression for the anisotropic part of the distribution, the telegraph equation is obtained (Earl 1976; for alternative expansion techniques, see also Gombosi et al. 1993; Pauls & Burger 1994).

Solutions of the telegraph equation are characterized by sharp propagating fronts that resemble those in our simulations. In order to perform a detailed comparison, we use the telegraph equation

$$\begin{equation} \frac{\partial F}{\partial t} + \tau \frac{\partial ^2 F}{\partial t^2} = \kappa _{\Vert ,{\rm BW}} \frac{\partial ^2 F}{\partial z^2} - u \frac{\partial F}{\partial z}, \end{equation} \tag{ 20 }$$

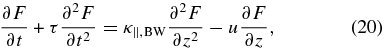
where, as before, the coherent speed u = κ_{||, BW}/L or u = ξκ_{||, BW} in our dimensionless variables. The telegraph equation formally reduces to the diffusion model when τ = 0. It is important to stress though that in practice τ does not vanish for any value of ξ. For instance, the reader can check that the results of Beeck & Wibberenz (1986) can be extended by obtaining a second iteration for g, which leads to τ ≈ 1 when ξ ≪ 1.

For an arbitrary focusing strength, we obtain an expression for τ in terms of ξ as follows. Equation (20) yields

$$\begin{equation} \frac{d \langle z \rangle }{d t} + \tau \frac{d^2 \langle z \rangle }{d t^2} = u, \end{equation} \tag{ 21 }$$

$$\begin{equation} \frac{d \langle z^2 \rangle }{d t} + \tau \frac{d^2 \langle z^2 \rangle }{d t^2} = 2 \kappa _{\Vert ,{\rm BW}} + 2 u \langle z \rangle. \end{equation} \tag{ 22 }$$

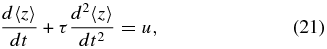
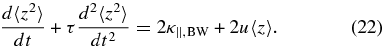
On assuming that d²〈z〉/dt² = 0 and d²var(z)/dt² = 0 for t > τ, the equations are combined to give

$$\begin{equation} \frac{1}{2} \frac{d}{dt} \mbox{var}(z) = \kappa _{\Vert ,{\rm BW}} - \tau u^2. \end{equation} \tag{ 23 }$$

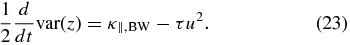
Comparing this with Equation (19) yields κ_{||, S} = κ_{||, BW} − τu². On substituting the expressions for κ_{||, BW} and κ_{||, S} from Equations (9) and (11) and solving for τ, we get

$$\begin{equation} \tau = \frac{\tanh \xi }{\xi }, \end{equation} \tag{ 24 }$$

which appears to be a new result.

Figure 9 compares the numerical results (histogram) and a solution to Equation (20) (dashed curve) for the density profile at time t = 8 in the case of strong focusing, ξ = 1.5. The initial conditions for the telegraph equation are F(z, 0) = δ(z) and ∂_tF(z, 0) = 0. An analytical solution of the equation in the context of focused transport is well known (Earl 1976). Since the solution is expressed in terms of special functions, however, in practice it is simpler to solve the telegraph equation numerically. We solved Equation (20) with τ given by Equation (24), using finite differences in space z and fourth-order Runge–Kutta in time (Press et al. 1986). An excellent agreement between the two density profiles strongly suggests that, wherever possible, a higher-order model should be used instead of the diffusion approximation in analysis of cosmic-ray data.

Zoom In Zoom Out Reset image size