H i-TO-H₂ TRANSITIONS AND H i COLUMN DENSITIES IN GALAXY STAR-FORMING REGIONS

Let N₂ be the H₂ column density (cm⁻²) at some depth normal to the cloud surface. Then, neglecting dust absorption of the LW photons, and for beamed radiation, the photodissociation rate (s⁻¹) for a single LW absorption line ℓ may be written as

$$\begin{equation} D_{\ell }(N_2) = \frac{1}{2} \int _0^\infty F_\nu \ \sigma _{\nu,d} \ {e}^{-\sigma _\nu N_2} \ d\nu = \frac{1}{2} F_\nu \ \frac{dW_{\ell,d}}{dN_2}, \end{equation} \tag{ 7 }$$

where

$$\begin{equation} W_{\ell,d}(N_2) \equiv \int _0^\infty [1 - \frac{\sigma _{\nu,d}}{\sigma _\nu }{e}^{-\sigma _\nu N_2}] \ d\nu. \end{equation} \tag{ 8 }$$

In these expressions, $F_\nu /2=2\pi {\cal I}_\nu ^{{\rm ISM}}I_{\rm UV}$ is the incident beamed flux density (photons cm⁻² s⁻¹ Hz⁻¹) at the cloud surface, σ_{ν, d} is the cross section (cm²) for absorptions that lead to molecular dissociation,⁵ and σ_ν is the cross section for all photon absorptions (not just those that are followed by dissociation). The dissociation probabilities, f_diss ≡ σ_{ν, d}/σ_ν, range from ∼0 to more than 0.5 for individual LW transitions depending on the rotational quantum number in the excited B or C states. The mean (typical) dissociation probability averaged over all lines is 〈f_diss〉 = 0.12. For a single absorption line,

$$\begin{equation} \sigma _d \equiv \int \sigma _{\nu,d} \ d\nu = \ f_{\rm diss} \ \frac{\pi e^2}{m_e c} \ f_{{\rm osc}} \ \simeq \ 2.7\times 10^{-5} \ {\rm cm}^2 \ {\rm Hz} \end{equation} \tag{ 9 }$$

for a typical LW-band oscillator strength of f_osc ≈ 0.01 and dissociation probability of f_diss ≈ 0.1 (and where e and m_e are the electron charge and mass, and c is the speed of light).

In Equation (7), we pull F_ν out of the integral because we assume that the flux density varies very slowly over the narrow line profile (as represented by σ_ν). In Equation (8), W_{ℓ, d}(N₂) is defined as the "equivalent bandwidth" (Hz) of radiation absorbed in H₂ dissociations via absorption line ℓ, up to molecular column N₂. The dissociation rate D_ℓ(N₂) decreases with the molecular column N₂ as the absorption line become optically thick, and the ratio

$$\begin{equation} f_{\ell, {\rm shield}}(N_2) \ \equiv \ \frac{D_{\ell }(N_2)}{D_{\ell }(0)}= \frac{1}{\sigma _d} \ \frac{dW_{\ell,d}}{dN_2} \end{equation} \tag{ 10 }$$

is the individual H₂-line "self-shielding" function. It quantifies the reduction of the line dissociation rate, where D_ℓ(0) is the line dissociation rate at the cloud surface. By definition, the self-shielding function is proportional to the derivative of the dissociation bandwidth W_{ℓ, d} (Federman et al. 1979; van Dishoeck & Black 1986; S88; Draine & Bertoldi 1996).

For the full multiline LW-band system, the dissociation rate (again neglecting dust absorption) may be written compactly as

$$\begin{equation} D(N_2) = \frac{1}{2}{\bar{F}_\nu } \ \frac{dW_d}{dN_2}, \end{equation} \tag{ 11 }$$

where W_d(N₂) is the equivalent dissociation bandwidth summed over all of the (possibly overlapping) absorption lines, and ${\bar{F}_\nu }$ is a mean flux density. A plot of W_d versus N₂ is the effective "curve of growth" for the dissociating LW radiation bandwidth in a dust-free cloud. We present computations for W_d(N₂) in Section 3 (the blue curve in Figure 3).

The mean flux density in Equation (11) is given by

$$\begin{equation} {\bar{F}_\nu } \ \equiv \ 4\pi \frac{\sum I_{{\nu _{ij}}}x_i \sigma _d^{ij}}{\sum x_i \sigma _d^{ij}}. \end{equation} \tag{ 12 }$$

Here x_i are the fractional populations of H₂ molecules in ro-vibrational levels i of the ground electronic X state, $I_{{\nu _{ij}}}$ is the (full 4π) free-space specific intensity at frequencies ν_ij of LW-band transitions between level i and levels j in the excited B or C states, and $\sigma _d^{ij}$ are the absorption line dissociation cross sections (cm² Hz). The mean flux density ${\bar{F}_\nu }$ is weighted by the relative strengths of the dissociation transitions. For the Draine spectrum, ${\bar{F}_\nu }=2.46\times 10^{-8} I_{\rm UV}$ photons cm⁻² s⁻¹ Hz⁻¹.

The denominator in expression (12) is the total (frequency integrated) H₂ dissociation cross section (cm² Hz) summed over all absorption lines,

$$\begin{equation} \sigma _d^{\rm tot}\equiv \sum x_i \sigma _d^{ij}. \end{equation} \tag{ 13 }$$

Most of the H₂-line absorptions occur out of the lowest few rotational levels, and the total effective dissociation cross section is insensitive to the fractional populations x_i. We find that

$$\begin{equation} \sigma _d^{\rm tot} = 2.36\times 10^{-3} \ \ \ {\rm cm}^{2} \ {\rm Hz}. \end{equation} \tag{ 14 }$$

The ratio $\sigma _d^{\rm tot}/\sigma _d\simeq 80$ is then the approximate number of strong LW absorption lines involved in the multiline H₂ photodissociation process (see also Figure 2 in Section 3).

With these definitions, the free-space photodissociation rate may be expressed as

$$\begin{equation} D_0 = {\bar{F}_\nu } \ \sigma _d^{\rm tot}. \end{equation} \tag{ 15 }$$

At a cloud surface the photodissociation rate is $D(0)\equiv D_0/2= ({1}/{2}){\bar{F}_\nu } \ \sigma _d^{\rm tot}$. The ratio

$$\begin{equation} f_{{\rm shield}}(N_2) \ \equiv \ \frac{D(N_2)}{D(0)}= \frac{1}{\sigma _d^{\rm tot}} \ \frac{dW_d}{dN_2} \end{equation} \tag{ 16 }$$

is then the complete multiline H₂ "self-shielding" function. It quantifies the reduction of the total dissociation rate due opacity in all of the absorption lines.

For a single line the self-shielding function varies as $N_2^{-1/2}$ for large N₂ because absorptions can always occur far out on the Lorentzian damping wings.⁶ Therefore, for a single absorption line, W_{ℓ, d} as given by Equation (8) diverges as $N_2^{1/2}$. For strong lines (with f_osc ∼ 0.01), this "square root" part of the curve of growth begins when N₂ ≳ 10¹⁷ cm⁻². For the realistic multiline system, the absorption lines will overlap for sufficiently large (≳ 5 × 10²⁰ cm⁻²) molecular columns, and W_d does not diverge as does W_{ℓ, d}. For the multiline system, the total dissociation bandwidth

$$\begin{equation} W_{d,{\rm tot}} \equiv \int _0^\infty \frac{dW_d}{dN_2} \ dN_2 \end{equation} \tag{ 17 }$$

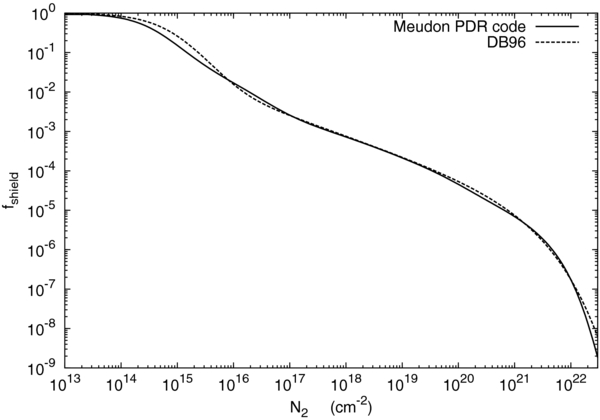
is limited to a finite maximal value (even in the absence of dust). We find that for the Draine spectrum W_{d, tot} = 9.1 × 10¹³ Hz (as computed in Section 3.1.2). In Section 3.1.3 we present our computations for the multiline self-shielding function (Figure 5). At the cloud surface, f_shield = 1. As the Doppler cores become optically thick at N₂ ≳ 10¹⁴ cm⁻², f_shield becomes small and the molecules are then said to self-shield against the dissociating radiation. The decline is more gradual at intermediate columns, 10¹⁷ to 10²² cm⁻², for which most of the absorption is out of the line wings. Finally, as line overlap occurs and the dissociating radiation is fully absorbed, f_shield becomes vanishingly small.

In the limit of complete line overlap, every photon in the (912–1108 Å) LW band is absorbed in H₂-lines. The product $({1}/{2}){\bar{F}}_\nu W_{d,{\rm tot}}$ is then the LW "dissociation flux" (photons cm⁻² s⁻¹) at the cloud surface. In the absence of dust absorption, this flux is equal to the H₂ dissociation rate per unit area. For complete absorption of the LW-band radiation, the mean dissociation probability is

$$\begin{equation} {\bar{f}}_{\rm diss} = \frac{{\bar{F}}_\nu W_{d,{\rm tot}}}{F_0}, \end{equation} \tag{ 18 }$$

where F₀/2 is the total incident LW-band flux. For the radiative transfer computations we present in Section 3, we find that ${\bar{f}}_{\rm diss}=0.12$ and is essentially equal to the simple average over the individual line dissociation probabilities for the matrix of X–B and X–C transitions. Our result for ${\bar{f}}_{\rm diss}$ is consistent with many previous calculations (e.g., Black & van Dishoeck 1987; Draine & Bertoldi 1996; Browning et al. 2003).

In addition to the H₂-line absorptions, the LW-band photons are also absorbed by dust grains, further reducing the photodissociation rate. We assume that the dust is mixed uniformly with the gas with a dust-to-gas mass ratio that depends linearly on the metallicity of the cloud. For the grain–photon interaction, we assume pure absorption and no scattering (or equivalently only forward scattering). With the inclusion of dust, the local dissociation rate, D, at any cloud depth is then

$$\begin{equation} D = \frac{1}{2}D_0 \ f_{{\rm shield}}(N_2) \ {e}^{-\tau _g}, \end{equation} \tag{ 19 }$$

where D₀ is the free-space dissociation rate (Equation (5)). In this expression, τ_g ≡ σ_gN is the dust continuum optical depth, where N ≡ N₁ + 2N₂ is the column density of hydrogen nuclei, in molecules plus atoms. Here σ_g is the dust grain LW-photon absorption cross section (cm²) per hydrogen nucleon. With the inclusion of dust attenuation, the dissociation rate given by Equation (19) depends on both N₂ and the column density of atomic hydrogen N₁.

For simplicity we also assume that σ_g is independent of photon frequency over the narrow LW band. For a standard interstellar extinction curve, with a total-to-selective extinction ratio of R_V ≡ A_V/E(B − V) = 3.1, a 1000 Å grain albedo ≈ 0.3, and a scattering asymmetry factor 〈cos θ〉 ≈ 0.6, the effective absorption cross section per hydrogen nucleus σ_g = 1.9 × 10⁻²¹ cm² (Draine 2003); R_V = 3.1 is for diffuse gas (with densities n ∼ 10² cm⁻³). For R_V = 3.1, A_V/N = 5.35 × 10⁻²² mag cm². In dense regions (n ≳ 10³ cm⁻³), R_V can be larger (up to ∼5.8) but with an extinction curve that is less steep toward the ultraviolet, with σ_g ≈ 8 × 10⁻²² cm⁻² (Cardelli et al. 1989; Fitzpatrick 1999; Draine & Bertoldi 1996; Draine 2011). With the assumption that the dust-to-gas mass ratio is linearly proportional to the metallicity Z' of the gas, we therefore set

$$\begin{equation} \sigma _g = 1.9\times 10^{-21} \phi _g \,Z^{\prime } \ {\rm cm}^2 \end{equation} \tag{ 20 }$$

where Z' = 1 corresponds to the solar photospheric abundances of the heavy elements ("solar metallicity") and where ϕ_g of order unity depends on the grain composition and size distribution.

Dust grains are also essential for H₂ formation (Hollenbach et al. 1971; Jura 1974; Barlow & Silk 1976; Leitch-Devlin & Williams 1985; Pirronello et al. 1997; Takahashi et al. 1999; Cazaux & Tielens 2002; Habart et al. 2004). We assume that per hydrogen nucleon the rate coefficient for H₂ formation on grains is given by

$$\begin{equation} R = 3\times 10^{-17} \ \left (\frac{T}{100 \ {\rm K}}\right)^{1/2} \,Z^{\prime } \ {\rm cm}^3 \ {\rm s}^{-1}, \end{equation} \tag{ 21 }$$

where T is the gas temperature in °K. Our standard value is then R = 3 × 10⁻¹⁷ cm³ s⁻¹ for T = 100 K and Z' = 1.

For a steady state in which molecular photodissociation is balanced everywhere by grain surface H₂ formation, the H i/H₂ formation–destruction equation may be written as

$$\begin{equation} Rn \ n_1 = \frac{1}{2}{\bar{F}_\nu } \ \frac{dW_d}{dN_2} \ {e}^{-\tau _g} \ n_2 = \frac{1}{2}D_0 \ f_{{\rm shield}}(N_2) \ {e}^{-\tau _g} \ n_2. \end{equation} \tag{ 22 }$$

In this equation, n₁ and n₂ are the local volume densities (cm⁻³) of the H i atoms and H₂ molecules, and

$$\begin{equation} n\equiv n_1+2n_2 \end{equation} \tag{ 23 }$$

is the total volume density of hydrogen nuclei. The right-hand side of Equation (22) is the H₂ photodissociation rate per unit volume (s⁻¹ cm⁻³) at some cloud depth where the rate is reduced by the combined effects of self-shielding and dust attenuation. The left-hand side is the rate per unit volume of H₂ formation on dust grains. We ignore all other formation or destruction processes (such as formation in the gas phase or destruction by X-ray or cosmic-ray ionization).

Given the free parameters n, D₀ (or equivalently I_UV), R, and σ_g (or given Z', which determines R and σ_g), Equation (22) together with particle conservation Equation (23) can be solved for the local atomic and molecular densities n₁ and n₂ and for the integrated atomic and molecular columns N₁ and N₂. If it is assumed that the incident LW radiation is fully absorbed, then (as we show below) Equation (22) gives our fundamental formula for the total atomic column that is maintained in the cloud.

The density ratio n₁/n₂ = dN₁/dN₂, and Equation (22) may be written as the separable differential equation (S88; see also Jura 1974; Hill & Hollenbach 1978):

$$\begin{equation} Rn \ {e}^{\sigma _g N_1} \,dN_1 = \frac{1}{2} {\bar{F}_\nu } \ \frac{dW_d}{dN_2} \ {e}^{-2\sigma _g N_2} \,dN_2. \end{equation} \tag{ 24 }$$

In writing the formation–destruction equation this way, a key insight is that the dust opacities associated with the atomic and molecular columns can be considered separately. We will refer to "H₂-dust" or "H i-dust" as the dust opacities associated with either just the H₂ or the H i gas, respectively, whether or not the H i gas is mixed with the H₂.

Integrating this expression and assuming that R and n are constants (i.e., do not vary with cloud depth) gives

$$\begin{equation} Rn \int _0^{N_1} {e}^{\sigma _g N^{\prime }_1} \ dN^{\prime }_ 1 = \frac{1}{2}{\bar{F}_\nu } \int _0^{N_2} \ \frac{dW_d}{dN^{\prime }_2} \ {e}^{-2\sigma _g N^{\prime }_2} \ dN^{\prime }_2, \end{equation} \tag{ 25 }$$

which is a functional relationship, N₁(N₂), between the atomic and molecular column densities. We note that the independent variable parameterizing the cloud depth is here chosen to be N₂ rather than the total gas column density N. Choosing N₂ as the independent variable is essential for our analysis, even though it is N that is proportional to the visual extinction A_V, or to the length scale z ≡ N/n.

Most importantly, for a given value of σ_g, the integral on the right-hand side of Equation (25),

$$\begin{equation} W_g(N_2) \equiv \int _0^{N_2} \ \frac{dW_d}{dN^{\prime }_2} \ {e}^{-2\sigma _g N^{\prime }_2} \ dN^{\prime }_2, \end{equation} \tag{ 26 }$$

is a function of the molecular column N₂ only. This is because the exponential cutoff factor in the integrand is due to H₂-dust opacity only—it excludes H i-dust—and because W_d itself depends only on N₂. Furthermore, W_g(N₂) is only very weakly dependent on n, R, or D₀ and is essentially independent of these parameters (see Section 3). So, for a given σ_g, the effective equivalent width W_g(N₂) is a quantity that can be calculated in advance as a "universal dust-limited curve of growth" for the H₂-line absorption of LW radiation, independent of the other parameters, n, R, and D₀, that together with σ_g determine the depth-dependent H i/H₂ density ratios and the H i-to-H₂ transition profiles.

Thus, W_g(N₂) (as opposed to W_d[N₂]) is the effective bandwidth of dissociating LW radiation in a dusty H₂ cloud, where now this bandwidth is limited by H₂-dust absorption of LW photons that would otherwise be available for H₂ photodissociation in a dust-free cloud. H₂-dust opacity is important if it becomes large before the H₂ absorption lines can fully overlap. For sufficiently small σ_g, the lines do overlap completely, and then W_g(N₂) = W_d(N₂). For sufficiently large σ_g, the H₂-dust provides a cutoff, and then W_g(N₂) < W_d(N₂) at large N₂.

It is a remarkable physical coincidence that the H₂ column density at which the H₂-lines begin to overlap—a column that depends on the internal molecular oscillator strengths and energy level spacings—is comparable to the H₂ column at which the H₂-dust opacity 2N₂σ_g ≳ 1 for standard interstellar dust absorption cross sections. Thus, both regimes of "small σ_g" and "large σ_g" for the dissociation bandwidth W_g(N₂) are relevant for the range of interstellar dust properties and metallicities in galaxies. In Section 3.1.2, we present computations of W_g(N₂) for a wide range of σ_g encompassing these regimes.

As N₂ → ∞, the equivalent width W_g(N₂) converges to a finite limit

$$\begin{equation} W_{g,{\rm tot}}(\sigma _g) \ \equiv \ \int _0^{\infty } \ \frac{dW_d}{dN_2} \ {e}^{-2\sigma _g N_2} \ dN_2, \end{equation} \tag{ 27 }$$

either because the exponential H₂-dust attenuation factor cuts off the integrand (for large σ_g) or because dW_d/dN₂ itself vanishes as the lines overlap (for small σ_g). Thus, W_{g, tot}(σ_g) is the total H₂-dust-limited effective dissociation bandwidth. For large σ_g, W_{g, tot} < W_{d, tot}, and for small σ_g, W_{g, tot} = W_{d, tot}. For large σ_g, the absorption lines remain separated but are nevertheless highly damped for most of the integration range up to the H₂-dust cutoff.

For a single absorption line, $dW_d/dN_2 \propto N_2^{-1/2}$ in the damped regime, and it follows from Equation (27) that W_{g, tot}(σ_g) scales as $\sigma _g^{-1/2}$. Our numerical computations (Section 3.1.2) show that for large σ_g this scaling behavior is maintained in the full multiline problem to a good approximation. In Section 3, we find that the simple formula

$$\begin{equation} W_{g,{\rm tot}}(\sigma _g) \ \simeq \ \frac{9.9 \times 10^{13}}{1 + (\sigma _g/ \ 7.2\times 10^{-22} \ {\rm cm}^{2})^{1/2}} \ {\rm Hz} \end{equation} \tag{ 28 }$$

is an excellent fit to our numerical radiative transfer results. The normalized H₂-dust-limited dissociation bandwidth

$$\begin{eqnarray} w \ &\equiv & \ \frac{W_{g,{\rm tot}}}{W_{d,{\rm tot}}} \ \simeq \ \frac{1}{1 + (\sigma _g/ \ 7.2\times 10^{-22} \ {\rm cm}^{2})^{1/2}} \nonumber\\ && = \frac{1}{1 + (2.64\phi _gZ^{\prime })^{1/2}}, \end{eqnarray} \tag{ 29 }$$

where in the last equality we have assumed σ_g = 1.9 × 10⁻²¹ϕ_gZ' (Equation (20)). In these expressions, W_{g, tot} → W_{d, tot} and w → 1 for small σ_g (low metallicity) and decrease as $\sigma _g^{-1/2}$ for large σ_g (high metallicity). The normalized bandwidth w decreases from 0.9 to 0.2 for σ_g ranging from 1 × 10⁻²³ cm⁻² (small) to ∼6 × 10⁻²¹ cm⁻² (large) or for Z' ranging from ∼0.01 to 3 (assuming σ_g∝Z'), which is the relevant range for galaxies.

Given Equation (18), we may now write

$$\begin{equation} {\bar{F}_\nu }W_{g,{\rm tot}} = w{\bar{f}}_{\rm diss}F_0, \end{equation} \tag{ 30 }$$

and define the effective dissociation probability

$$\begin{equation} {\bar{p}}_{\rm diss} \equiv \frac{{\bar{F}_\nu } W_{g,{\rm tot}}}{F_0} \ \equiv \ w{\bar{f}}_{\rm diss}. \end{equation} \tag{ 31 }$$

The product $({1}/{2}){\bar{F}_\nu }W_{g,{\rm tot}}$ is the "effective dissociation flux" for dusty clouds in which H₂-dust may absorb some of the incident LW radiation. The effective dissociation flux depends on the competition between H₂-line absorption and H₂-dust absorption as given by the dependence of W_{g, tot} on σ_g. The effective dissociation flux is the H₂ photodissociation rate per unit surface area for a dusty and optically thick molecular slab in which H i-dust opacity is negligible.

When H₂-dust is negligible, w = 1 and ${\bar{p}}_{\rm diss}={\bar{f}}_{\rm diss}$. When H₂-dust opacity is significant, w < 1 and ${\bar{p}}_{\rm diss}<{\bar{f}}_{\rm diss}$. The effective dissociation probability ${\bar{p}}_{\rm diss}$ is the fraction of the total 912–1108 Å LW-band flux that is absorbed in H₂ photodissociation events in a dusty, optically thick, predominantly molecular slab (with vanishing H i-dust opacity). For low Z', ${\bar{p}}_{\rm diss}=0.12$ is a constant. For high Z', ${\bar{p}}_{\rm diss}$ decreases as Z'^−1/2.

Returning now to Equation (25), it follows that

$$\begin{equation} Rn \int _0^{N_{1}}{e}^{\sigma _g N^{\prime }_1} dN^{\prime }_ 1 = \frac{1}{\sigma _g}Rn[{e}^{\sigma _g N_1}-1] = \frac{1}{2}{\bar{F}_\nu } W_g(N_2) \ \ \ \end{equation} \tag{ 32 }$$

or

$$\begin{equation} N_1(N_2) = \frac{1}{\sigma _g} \ {\rm ln}\left [\frac{1}{2}\frac{\sigma _g {\bar{F}}_\nu W_g(N_2)}{Rn} + 1\right ]. \end{equation} \tag{ 33 }$$

Following S88, we now define the dimensionless parameter

$$\begin{equation} \alpha \ \equiv \ \frac{D_0}{Rn} = \frac{\sigma _d^{\rm tot}{\bar{F}}_\nu }{Rn}, \end{equation} \tag{ 34 }$$

where D₀ is the free-space dissociation rate,⁷ and we define the dimensionless "G integral"

$$\begin{equation} G(N_2) \ \equiv \ \sigma _g \int _0^{N_2} f_{{\rm shield}}(N^{\prime }_2) \ {e}^{-2\sigma _g N^{\prime }_2} \ dN^{\prime }_2 = \frac{\sigma _g}{\sigma _d^{\rm tot}} W_g(N_2). \end{equation} \tag{ 35 }$$

We can then write

$$\begin{equation} N_1(N_2) = \frac{1}{\sigma _g}{\rm ln}\left[\frac{\alpha G(N_2)}{2} + 1\right], \ \ \ \end{equation} \tag{ 36 }$$

where

$$\begin{equation} \alpha G(N_2) = \frac{\sigma _g{\bar{F}_\nu } W_g(N_2)}{Rn}. \end{equation} \tag{ 37 }$$

Given the "universal" dust-limited curve of growth W_g(N₂), which can be computed "in advance" for any σ_g, the atomic column is then given by Equation (36) (or Equation (33)) for any surface dissociation rate D₀ (or I_UV), rate coefficient R, and density n.

We refer to Equation (36) as the "semi-analytic integral H i-to-H₂ profile." It shows that the H i column at any depth depends on only two quantities—σ_g and αG(N₂). In dimensionless form

$$\begin{equation} \tau _1(\tau _2) = {\rm ln}\left[\frac{\alpha G(\tau _2)}{2}+ 1\right], \end{equation} \tag{ 38 }$$

where τ₂ ≡ 2σ_gN₂ is the dust optical depth associated with the molecular column, and τ₁(τ₂) ≡ σ_gN₁ is the H i-dust optical depth at τ₂.

As N₂ → ∞, W_g(N₂) → W_{g, tot}. The total atomic column density is therefore finite and is given by

$$\begin{equation} N_{1,{\rm tot}} = \frac{1}{\sigma _g} \ {\rm ln}\left[\!\frac{1}{2}\frac{\sigma _g{\bar{F}_\nu } W_{g,{\rm tot}}}{Rn} +1 \!\right] = \frac{1}{\sigma _g} \ {\rm ln}\left[\! \frac{1}{2}{\bar{f}}_{\rm diss}\frac{\sigma _g wF_0}{Rn} + 1 \!\right] \end{equation} \tag{ 39 }$$

or

$$\begin{equation} N_{1,{\rm tot}} = \frac{1}{\sigma _g}{\rm ln}\left[\frac{\alpha G}{2} + 1\right]. \end{equation} \tag{ 40 }$$

Here the dimensionless parameter

$$\begin{equation} G(\sigma _g) \ \equiv \ \frac{\sigma _g}{\sigma _d^{\rm tot}} W_{g,{\rm tot}}(\sigma _g) \ \ \ \end{equation} \tag{ 41 }$$

is the limit of G(N₂) as N₂ → ∞, so that

$$\begin{equation} \alpha G = \frac{D_0G}{Rn} = \frac{\sigma _g{\bar{F}}_\nu W_{g,{\rm tot}}}{Rn} = {\bar{f}}_{\rm diss}\frac{\sigma _g wF_0}{Rn}. \end{equation} \tag{ 42 }$$

We discuss these and additional expressions for αG in Section 2.2.6 below.

Equation (40) for the total H i column on one side of an optically thick cloud was first derived by S88 (see Equation (9) of that paper), and it is the fundamental relation in our analysis.⁸ The basic assumption is that all of the dissociating LW-band radiation is absorbed, as in a classical "ionization-bounded" H ii region or layer (Strömgren 1939). However, because of the three-way competition between H i-dust, H₂-dust, and H₂-lines, the behavior for H i is more complicated than for H ii. For a steady (dust-free) photoionized planar Strömgren layer, the H ii column equals the ratio of the Lyman continuum flux to the recombination rate, independent of the photoionization cross section. Similarly, in our Equation (39) or Equation (40), the H₂-line absorption cross section does not appear explicitly (although it is implicit in our definition of the effective dissociation flux). The H i column depends on the ratio of the effective dissociation flux to the H₂ formation rate, but this ratio is multiplied by the dust absorption cross section and appears inside a logarithm. We discuss this behavior, and the connection to Strömgren relations, in our description of the weak- and strong-field limits in Section 2.2.8.

In dimensionless form, the total H i-dust optical depth associated with the total atomic column is

$$\begin{equation} \tau _{1,{\rm tot}} = {\rm ln}\left[\frac{\alpha G}{2} + 1\right]. \end{equation} \tag{ 43 }$$

The total H i-dust optical depth depends on the single dimensionless parameter αG constructed from the cloud variables D₀ (or F₀ or I_UV), n, R, and σ_g (or Z', which determines R and σ_g).

The total gas column N ≡ N₁(N₂) + 2N₂. It therefore follows from Equation (36) that the atomic column as a function of the total (atomic plus molecular) column, N₁(N), also depends on just σ_g and αG. Similarly, for τ_g ≡ σ_gN, the H i-dust optical depth τ₁(τ_g) depends on the single dimensionless parameter αG. Then, since n₁/n₂ ≡ dN₁/dN₂ it follows that the shapes of the H i-to-H₂ transition profiles are invariant for identical αG. That is, the density fractions n₁/n and 2n₂/n expressed as functions of the dust optical depth τ_g (or visual extinction A_V) depend on just the single dimensionless parameter αG.

In Section 3.1.4 we present detailed numerical computations for the H i-to-H₂ transition profiles. We show that the transitions are "gradual" when αG ≪ 1 and are "sharp" when αG ≫ 1. An essential feature of our derivation and analytic expression for the total H i column is that no assumptions need to be made on the shape of the H i-to-H₂ transition profile. Our Equation (39) or Equation (40) are universally valid for all profile shapes, gradual or sharp.

It is useful to consider the physical meaning of the dimensionless parameters α and G and their product αG.

First, α is the ratio of the unattenuated free-space H₂ photodissociation rate to the H₂ formation rate and can be expressed as

$$\begin{eqnarray} \alpha &=& 1.93\times 10^4 \ \left (\frac{D_0}{5.8\times 10^{-11} \ {\rm s}^{-1}}\right) \left (\frac{3\times 10^{-17} \ {\rm cm}^3 \ {\rm s}^{-1}}{R}\right) \nonumber\\ && \times \left (\frac{100 \ {\rm cm}^{-3}}{n}\right). \end{eqnarray} \tag{ 44 }$$

Thus, α is just the free-space atomic-to-molecular density ratio n₁/n₂, and α/2 is the density ratio at the surface of an optically thick slab. For a characteristic interstellar cloud gas density n ∼ 10² cm⁻³, and with D₀ = 5.8 × 10⁻¹¹I_UV s⁻¹, the atomic-to-molecular density ratio is n₁/n₂ ≫ 1 at the cloud edge in the absence of shielding, unless I_UV is unrealistically small. Conversion to the molecular phase in the ISM generally requires significant attenuation of the ambient and destructive radiation fields.

Now consider the parameter G. Defining the H₂-dust opacity τ₂ ≡ 2σ_gN₂ (see Equation (35)),

$$\begin{eqnarray} G &=& \frac{1}{2}\int _0^\infty f_{{\rm shield}}(\tau _2){e}^{-\tau _2} \ d\tau _2 \equiv \frac{1}{2} \langle {f_{{\rm shield}}}\rangle \nonumber\\ &\approx & \frac{1}{2}\int _0^1 f_{{\rm shield}}(\tau _2) \ d\tau _2. \end{eqnarray} \tag{ 45 }$$

Thus, G is the average H₂ self-shielding factor. The average is over an H₂ column for which the H₂-dust opacity τ₂ ≈ 1. Thus, (1/2)D₀G is the characteristic photodissociation rate for self-shielded H₂ in a fully molecular cloud, prior to the onset of any H₂-dust attenuation. Because f_shield is already ≪1 for τ₂ ≪ 1, the H₂ molecules are very self-shielded for an H₂-dust opacity τ₂ ∼ 1, and G is generally very small.

The product αG/2 = (1/2)D₀G/Rn is then the atomic-to-molecular density ratio n₁/n₂ for the average shielded H₂ dissociation rate. This is our first interpretation for αG (and as adopted in S88). If n₁ > 2n₂ for the shielded dissociation rate, then H i-dust must also contribute to the attenuation of the LW radiation since then τ₁ > τ₂ within the H₂-dust attenuation column. If n₁ ≪ 2n₂, then H i-dust attenuation is negligible.

Alternatively, $G\equiv \sigma _gW_{g,{\rm tot}}/\sigma _d^{\rm tot}$ (Equation (41)) is the ratio of the UV continuum dust absorption cross section (cm²) to the total H₂-line dissociation cross section (cm² Hz) averaged over the effective dissociation bandwidth (Hz). Again, G is generally very small because H₂-line absorption is so much more efficient than dust absorption. Given σ_g = 1.9 × 10⁻²¹ϕ_gZ' cm² (Equation (20)) and our expression (28) for W_{g, tot}, and with $\sigma _d^{\rm tot}=2.36 \times 10^{-3}$ cm² Hz, we have

$$\begin{equation} G \ \simeq \ \frac{7.97\times 10^{-5} Z^{\prime } \phi _g}{1 \ + \ (2.64Z^{\prime }\phi _g)^{1/2}}. \end{equation} \tag{ 46 }$$

For example, for standard values Z' = 1 and ϕ_g = 1, Equation (46) gives G = 3.0 × 10⁻⁵ and the shielded H₂ dissociation rate (1/2)D₀G = 8.7 × 10⁻¹⁶I_UV s⁻¹. For low metallicity, small σ_g, it follows that G∝Z' (or G∝σ_g). For high metallicity, large σ_g, G∝Z'^1/2 (or $G\propto \sigma _g^{1/2}$).

Since α is the free-space atomic-to-molecular density ratio, we have

$$\begin{eqnarray} \alpha G &=& \frac{\sigma _gW_{g,{\rm tot}}}{\sigma _d^{\rm tot}}\frac{n_1}{n_2} \ \ \left \vert\right. _{\rm free space} \nonumber \\ & =& \frac{\sigma _g {\bar{F}}_\nu W_{g,{\rm tot}} n_1}{D_0n_2} \ \ \left \vert\right. _{\rm free space} \nonumber\\ &=& \frac{{\bar{f}}_{\rm diss} w F_0 \sigma _g n_1}{D_0n_2} \ \ \left \vert\right. _{\rm free space}, \end{eqnarray} \tag{ 47 }$$

where in the second and third equalities we have used the relations $D_0\equiv \sigma _d^{\rm tot}{\bar{F}}_\nu$ and ${\bar{F}}_\nu W_{g,{\rm tot}}\equiv {\bar{f}}_{\rm diss}w F_0$. This gives our second interpretation for αG. It is the free-space ratio of the H i-dust to H₂-line absorption rates of LW photons in the H₂-dust-limited dissociation band.

Third, since $D_0G={\bar{f}}_{\rm diss}\sigma _g wF_0$ (and ${\bar{p}}_{\rm diss}\equiv w{\bar{f}}_{\rm diss}$), we have

$$\begin{equation} \alpha G = {\bar{f}}_{\rm diss}\frac{\sigma _g wF_0}{Rn} = {\bar{p}}_{\rm diss}\frac{\sigma _g F_0}{Rn}. \end{equation} \tag{ 48 }$$

Thus, αG is the free-space ratio of the dust absorption rate of the effective dissociation flux—per hydrogen atom—to the molecular formation rate per atom.

When αG ≪ 1, H i-dust plays no role anywhere in the cloud, since it is negligible even for the free-space field where the atomic density is largest. However, when αG ≫ 1, H i-dust becomes important and absorbs an increasing fraction of the LW photons that are otherwise available for H₂ photodissociation.

Thus, with Equations (44) and (46),

$$\begin{eqnarray} \alpha G &=& 1.54 \ \left (\frac{D_0}{5.8\times 10^{-11} \ {\rm s}^{-1}}\right) \left (\frac{3\times 10^{-17} \ {\rm cm}^3 \ {\rm s}^{-1}}{R}\right) \nonumber\\ && \times \left (\frac{100 \ {\rm cm}^{-3}}{n}\right) \ \frac{\phi _gZ^{\prime }}{1+(2.64\phi _gZ^{\prime })^{1/2}}, \end{eqnarray} \tag{ 49 }$$

or with Equation (48),

$$\begin{eqnarray} \alpha G &=& 1.54 \ \left (\frac{\sigma _g}{1.9\times 10^{-21} \ {\rm cm}^2}\right) \left (\frac{F_0}{2.07\times 10^7 \ {\rm cm}^{-2} \ {\rm s}^{-1}}\right) \nonumber\\ && \times \left (\frac{3\times 10^{-17} \ {\rm cm}^3 \ {\rm s}^{-1}}{R}\right) \left (\frac{100 \ {\rm cm}^{-3}}{n}\right)\ \nonumber\\ && \times \frac{1}{1+(2.64\phi _gZ^{\prime })^{1/2}}. \end{eqnarray} \tag{ 50 }$$

With Equation (4) or Equation (5) for F₀ or D₀, and Equations (20) and (21) for σ_g and R, we then have

$$\begin{equation} \alpha G = 1.54 \ \frac{I_{\rm UV}}{(n/100\, {\rm cm}^{-3})} \ \frac{\phi _g}{1+(2.64\phi _gZ^{\prime })^{1/2}}. \end{equation} \tag{ 51 }$$

For σ_g and R varying the same way with Z' there is a cancellation, but a metallicity dependence still remains via the dissociation bandwidth w (Equation (29)) and its dependence on the competition between H₂-dust absorption and H₂-line absorption. For low Z' (complete line overlap limit, w = 1), αG is independent of the metallicity, but for high Z', $w\sim \sigma _g^{-1/2}$ and αG ∼ Z'^−1/2.

Expression (51) also shows that the regimes of large and small αG are both relevant for the widely varying conditions in localized environments of the ISM in galaxies. For example, I_UV can range from ∼1 at "average" locations to ≳ 10⁵ near hot stars, whereas n can range from ∼10 cm⁻³ in diffuse gas to ≳ 10⁶ cm⁻³ in dense molecular clouds. On global scales in star-forming galaxy disks, I_UV and n may be correlated (see Section 2.2.9). But on small scales, enhanced radiation fields will not necessarily be offset by higher gas densities, and I_UV/n may span a wide range from "large" to "small."

For αG/2 ≪ 1 the absorption of the LW radiation is dominated by the combination of H₂-line absorption and H₂-dust absorption, and H i-dust is negligible.⁹ For αG/2 ≫ 1 H i-dust absorption dominates the attenuation of the radiation field. We refer to αG/2 ≪ 1 as the "weak-field limit" and to αG/2 ≫ 1 as the "strong-field limit."

We now consider the behavior of N_{1, tot} in these two limits.

It follows from Equations (40) and (39) that for αG/2 ≪ 1,

$$\begin{eqnarray} &&N_{1,{\rm tot}} = \frac{1}{\sigma _g}\frac{\alpha G}{2} = \frac{1}{2}\frac{1}{\sigma _g}\frac{D_0}{Rn} G = \frac{1}{2} \frac{{\bar{F}_\nu } W_{g,{\rm tot}}}{Rn} = \frac{1}{2}{\bar{f}}_{\rm diss}\frac{wF_0}{Rn}.\nonumber \\ \end{eqnarray} \tag{ 52 }$$

So for weak fields, the total H i column density is equal to the ratio of the effective LW dissociation flux to the H₂ formation rate (which is the removal rate of for the H i). The atomic column is proportional to the surface dissociation rate D₀ (or to the field strength I_UV) and inversely proportional to the cloud gas density n.

In the weak-field limit, the H i-dust opacity associated with the total atomic column τ_{1, tot} ≡ σ_gN_{1, tot} ≪ 1. We again see that H i-dust plays no role in attenuating the LW radiation field in this limit. For weak fields, the total H i column depends on σ_g only via W_{g, tot}, through the possible competition between H₂-line absorption and H₂-dust absorption. For small σ_g where H₂-dust is negligible, dust absorption plays no role whatsoever, and N_{1, tot} is completely independent of σ_g. In the small-σ_g limit, G∝σ_g, and the dust absorption cross section cancels out completely. For R∝Z', we then have N_{1, tot}∝1/Z', and the metallicity dependence enters entirely via the H₂ formation rate coefficient. For large σ_g, H₂-dust absorption is non-negligible, and $W_{g,{\rm tot}} \propto \sigma _g^{-1/2}$ (and $G\propto \sigma _g^{1/2}$), thus N_{1, tot} scales as $\sigma _g^{-1/2}$. Then with σ_g∝Z' and R∝Z', we have N_{1, tot}∝Z'^−3/2.

Expression (52) can be written as the simple "Strömgren relation"¹⁰

$$\begin{equation} Rn N_{1,{\rm tot}} = \frac{1}{2}{\bar{F}}_\nu W_{g,{\rm tot}}. \end{equation} \tag{ 53 }$$

The effective dissociation flux on the right-hand side is the rate per unit area at which dissociating photons (those absorbed in H₂-lines but not by H₂-dust) penetrate the cloud surface. By definition these photons are fully absorbed by the H₂ when H i-dust is negligible, so this is also the photodissociation rate per unit surface area. In steady state this must equal the total H₂ formation rate per unit area, which is the left-hand side.

For the strong-field limit αG/2 ≫ 1, it follows from Equation (40) that

$$\begin{eqnarray} N_{1,{\rm tot}} &=& \frac{1}{\sigma _g}{\rm ln}\left[\frac{\alpha G}{2}\right] = \frac{1}{\sigma _g}{\rm ln}\left[\frac{1}{2}\frac{D_0 G}{Rn}\right] \nonumber\\ & =& \frac{1}{\sigma _g}{\rm ln}\left [\frac{1}{2}\frac{\sigma _g{\bar{F}_\nu } W_{g,{\rm tot}}}{Rn}\right ] = \frac{1}{\sigma _g}{\rm ln}\left [\frac{1}{2}{\bar{f}}_{\rm diss}\frac{\sigma _g wF_0}{Rn}\right ]. \quad\quad \end{eqnarray} \tag{ 54 }$$

For strong fields, τ_{1, tot} = σ_gN_{1, tot} ≳ 1, and the H i-dust opacity associated with the total atomic column contributes significantly to the attenuation of the incident LW flux. This leads to a saturation and logarithmic dependence of the atomic column on the cloud parameters. For example, increasing the atomic column by increasing the LW-band flux also leads to more effective absorption of the LW photons by the larger H i-dust column. A decreasing fraction of the LW photons is then absorbed by the H₂, and the growth of the atomic column is limited. Similarly, increasing the H₂ formation rate reduces the atomic column, but the H i-dust opacity is then also reduced, which increases the LW fraction available for photodissociation, thereby moderating the reduction of the H i column.

If we neglect the logarithmic factor, then up to a factor of order unity, we have

$$\begin{equation} N_{1,{\rm tot}} \ \approx \ 1/\sigma _g \end{equation} \tag{ 55 }$$

for intense fields. Indeed, if the attenuation is dominated by H i-dust, the atomic column must approach a value such that τ_{1, tot} ≡ σ_gN_{1, tot} ≳ 1. Then, if σ_g∝Z' the H i column N_{1, tot}∝1/Z' (neglecting the logarithmic factor). In the strong-field limit, the metallicity dependence enters via the grain absorption cross section.

Finally, Equation (54) for the strong-field limit may also be expressed as the Strömgren relation¹¹

$$\begin{equation} Rn N_{1,{\rm tot}} = \frac{1}{2} {\bar{F}}_\nu W_{g,{\rm tot}} \ u. \end{equation} \tag{ 56 }$$

Here

$$\begin{equation} u \equiv \tau _{1,{\rm tot}} \ {e}^{-\tau _{1,{\rm tot}}} \end{equation} \tag{ 57 }$$

is a reduction factor that accounts for H i-dust attenuation of the effective dissociation flux. The right-hand side of Equation (56), including the factor u, is the H₂ photodissociation rate per unit surface area, and this equals the total H₂ formation rate per unit area, which is the left-hand side.

Galaxy disks may be self-regulated such that the thermal pressures in the H i gas enable a cold/warm (CNM/WNM) two-phased mixture, with cold neutral Hi (CNM) accumulating in the UV illuminated PDRs of the star-forming molecular clouds (Ostriker et al. 2010; Faucher-Giguère et al. 2013; Kim et al. 2013). As invoked by KMT/MK10, the ratio I_UV/n may then be restricted to a narrow range. This then gives rise to a characteristic αG for self-regulated disks, as follows.

For a given heating rate, two-phased equilibrium occurs for a narrow range of thermal pressures and associated CNM and WNM densities, n_CNM and n_WNM, as controlled by the combined action of Lyα and C ii fine-structure emission line cooling, with a metallicity dependence via the abundance of the gas-phase carbon ions (Field et al. 1969; Wolfire et al. 2003). Given the FUV heating rates and the metallicity-dependent emission line cooling rates, the characteristic CNM density for two-phase equilibrium will be close to the minimum gas density for which CNM is possible. Wolfire et al. (2003) developed the analytic formula

$$\begin{equation} n_{\rm CNM} =\frac{31\phi _{\rm CNM}}{1 + 3.1Z^{\prime 0.365}}I_{\rm UV} \ {\rm cm}^{-3}, \end{equation} \tag{ 58 }$$

for the characteristic CNM density, assuming that FUV grain photoelectric emission is the dominant heating mechanism for the gas. In this expression, I_UV is again the FUV intensity (normalized to the Draine field), Z' is the metallicity, and ϕ_CNM is a factor of order unity. Following KMT/MK10 we set ϕ_CNM = 3. This gives n_CNM = 23 cm⁻³ for I_UV = 1, at Z' = 1.

Most importantly, n_CNM is proportional to I_UV. If the gas density n in the FUV illuminated gas is set equal to n_CNM, the ratio I_UV/n then depends on the metallicity only, as given by Equation (58). With Equation (51) we then have

$$\begin{equation} (\alpha G)_{\rm CNM} = 6.78 \ \left (\frac{1 + 3.1 Z^{\prime 0.365}}{4.1}\right)\frac{\phi _g}{1 + (2.64 \phi _gZ^{\prime })^{1/2}} \end{equation} \tag{ 59 }$$

for self-regulated systems. In Figure 1 the solid curve is (αG)_CNM versus Z' as given by Equation (59) (assuming ϕ_g = 1). The dashed curve excludes the (2.64ϕ_gZ')^1/2 term that accounts for H₂-dust reduction of the effective dissociation bandwidth (not considered by KMT/MK10 as discussed in Section 4). Remarkably, the enhanced n_CNM associated with reduced cooling efficiency at low metallicity (Equation (58) is offset by the increased dissociation bandwidth at low Z'. Thus, so long as grain photoelectric heating dominates, we have

$$\begin{equation} \frac{(\alpha G)_{\rm CNM}}{2}\ \approx \ 1 \end{equation} \tag{ 60 }$$

for self-regulated systems, independent of Z'. The expected H i columns are then midway between the weak- and strong-field limits.

Zoom In Zoom Out Reset image size

The optically thin (full 4π) free-space (optically thin) H₂ photodissociation rate, D₀, is a fundamental parameter for ISM and galaxy evolution studies, and we have recalculated it here for the Draine FUV spectrum (Equation (2)). In Table 1, and for I_UV = 1, we list the free-space UV excitation rates, P_vj (s⁻¹) out of the 14 lowest-lying H₂ (v, j) ro-vibrational levels. Each rate is summed over all upward LW transitions. We also list the mean dissociation probabilities 〈f_diss〉_vj, averaged over all of the transitions, and the resulting dissociation rates, D_vj (s⁻¹) out of each (v, j) level. Our numbers are consistent with Draine & Bertoldi (1996) (see their Table 2), who used our basic input molecular data sets.

The total dissociation rate is weighted by the population fractions x_vj but is insensitive to the gas temperature or density when the excitation is mainly out of the lowest few j levels. For T between 10 to 10³ K, and for n ranging from 10 to 10⁶ cm⁻³, we find that to within at most a 2% variation, D₀ = 5.8 × 10⁻¹¹ s⁻¹ for I_UV = 1. The dissociation rate is essentially proportional to the field intensity. For very intense fields, the rate is increased by enhanced excitation of the rotational states and photodissociation out of these states by photons longward of 1108 Å, outside our nominal LW band. For T = 100 K, and n = 100 cm⁻³, we find that for I_UV from 1 to 10³, D₀ = 5.8 × 10⁻¹¹ϕ_exI_UV s⁻¹, where the "rotational excitation factor" ϕ_ex increases from 1 to 1.5 for this range of field intensities. We have also computed the mean flux density in the free-space radiation field, as defined by Equation (12). For the Draine spectrum, we find that ${\bar{F}}_\nu =2.46\times 10^{-8}\phi _{\rm ex}I_{\rm UV}$ photons cm⁻² s⁻¹ Hz⁻¹ for the same range of T, n, and I_UV. For the analysis we present in Section 2, we assume ϕ_ex = 1.

As discussed in Section 2.2.4, the "H₂-dust-limited dissociation bandwidth" W_g(N₂) (Equation (26)) is a fundamental quantity for the H i-to-H₂ transitions and the buildup of the H i column densities.

In Figure 3 we plot our curve-of-growth computations for W_g(N₂) integrated over all of the LW-band absorption lines, for σ_g ranging from 1.9 × 10⁻²⁰ to 1.9 × 10⁻²³ cm², corresponding to metallicities Z' from 0.01 to 10. We set the Doppler-b parameters for all of the lines equal to a typical ISM cloud value of 2 km s⁻¹. Our results are insensitive to the precise choice for b because the dominant absorption lines are very highly damped. We extract the W_g(N₂) curves from our numerical radiative transfer computations for the radiation flux absorbed in the lines, self-consistently accounting for the flux reduction due to the presence of H₂-dust. For any σ_g, the curve of growth W_g(N₂) depends primarily on the internal molecular oscillator strengths, line profile cross sections, and dissociation probabilities for the excited states. We have verified by explicit computations that W_g(N₂) is indeed very insensitive to external cloud parameters such as the field intensity I_UV and/or gas density n, or temperature T. The curves of growth are also insensitive to the rotational-level distributions and ortho-to-para H₂ ratio. The specific curves displayed in Figure 3 were extracted from model runs with I_UV = 4, n = 10⁵ cm⁻³, and T = 100 K, and for a constant ortho-to-para ratio set equal to 3 (with H⁺–H₂ proton exchange reactions turned off).

Zoom In Zoom Out Reset image size

For N₂ ≲ 10¹⁴ cm⁻², all of the lines are optically thin, and W_g increases linearly with N₂. Between 10¹⁵ and 10¹⁷ cm⁻², the growth is logarithmic as the Doppler cores become optically thick. At larger columns, W_g increases more rapidly again as absorptions start occurring out of the line wings. For N₂ between 10¹⁸ and 10²⁰ cm⁻², we find that W_g grows as $N_2^{3/8}$, a bit more slowly than for a single damped line (for which it would be $N_2^{1/2}$).

The W_g saturates at sufficiently large H₂ columns. When H₂-dust is negligible, the entire LW band is absorbed in fully overlapping lines, and W_g reaches a maximal value of 9 × 10¹³ Hz, for N₂ ≳ 10²² cm⁻². In Figure 3 the absorption is essentially dust-free for σ_g = 1.9 × 10⁻²³ cm², since the lines overlap before the H₂-dust opacity becomes significant, and for the (blue) curve W_g(N₂) = W_d(N₂) (see Sections 2.2.1 and 2.2.4). For larger σ_g, and for N₂ ≳ 1/(2σ_g), the asymptotic W_g is limited by H₂-dust opacity.

Figure 4 shows our results for the "total dust-limited bandwidth" W_{g, tot}(σ_g) (Equation (27)) for σ_g from 10⁻²⁴ to 10⁻²⁰ cm². The points are our numerical results, and the solid curve is our analytic representationg

$$\begin{equation} W_{g,{\rm tot}}(\sigma _g) \ \simeq \ \frac{9.9 \times 10^{13}}{1 + (\sigma _g/ \ 7.2\times 10^{-22} \ {\rm cm}^{2})^{1/2}}\ {\rm Hz}, \end{equation} \tag{ 71 }$$

as already introduced in Section 2. This expression is accurate to within 4% compared with the numerical results. The transition from the line overlap to H₂-dust-limited regimes (small to large σ_g) occurs at σ_g ∼ 7.2 × 10⁻²² cm². Line overlap is just starting to become important for solar (Z' ∼ 1) metallicities. For a fully molecular slab, most of the LW-band radiation is absorbed by H₂-dust for Z' ≳ 0.5. For Z' ≲ 0.5, most of the radiation is absorbed in H₂-lines. Our results show that the regimes of small and large σ_g are both relevant for the realistic range of metallicities in galaxies.

Zoom In Zoom Out Reset image size

To a good approximation $W_{g,{\rm tot}}\propto \sigma _g^{-1/2}$ for large σ_g as indicated by our numerical results and Equation (28). This is the expected scaling for a single (effective) damped absorption line in competition with H₂-dust (see Section 2.2.4). We adopt $W_{g,{\rm tot}}\propto \sigma _g^{-1/2}$ for large σ_g for our analytic scaling relations in Section 2, although W_g(N₂) grows somewhat more slowly with N₂ than for a single line.

By definition, the H₂ "self-shielding function" $f_{{\rm shield}}(N_2)\equiv (1/\sigma _d^{\rm tot})dW_d/dN_2$, where W_d(N₂) is the dissociation bandwidth for vanishing σ_g (see Equation (16)).

In Figure 5 we plot (solid curve) our numerically computed derivative f_shield(N₂). We also plot (dashed) the Draine & Bertoldi (1996) fit (their Equation (37)) for the shielding function, given by

$$\begin{eqnarray} f_{{\rm shield}}(N_2) &=& \frac{0.965}{(1+x/b_5)^2} +\frac{0.035}{(1+x)^{0.5}} \nonumber\\ &&\times {\rm exp}[-8.5\times 10^{-4}(1\, +\, x)^{0.5}], \end{eqnarray} \tag{ 72 }$$

where x = N₂/5 × 10¹⁴cm⁻² and b₅ = b/10⁵ cm s⁻¹ (we assume b₅ = 2). It is evident that our computed shielding function is in excellent agreement with this formula.

Zoom In Zoom Out Reset image size

At low N₂, the lines are optically thin and f_shield = 1. As the line cores become optically thick for N₂ ≳ 10¹⁴ cm⁻², the molecules "self-shield" and f_shield decreases. By 10¹⁸ cm⁻², f_shield = 5 × 10⁻⁴. Between 10¹⁸ and 10²⁰ cm⁻², the shielding function declines as $N_2^{-5/8}$, as expected given the (integral) behavior of W_d(N₂) in this range. Finally, at larger columns f_shield drops sharply as the lines fully overlap. As found by Draine & Bertoldi (1996), the reduction due to line overlap sets in at a column of 3 × 10²⁰ cm⁻². We again see that attenuation due to line overlap becomes important for Z' ≲ 1. For such metallicities, H₂-dust opacity becomes significant only at columns 1/(2σ_g) ≳ 3 × 10²⁰ cm⁻², at which point the lines have already overlapped and the LW photons fully absorbed.

In Figure 6 we plot the "average self-shielding factor," $G \equiv (\sigma _g/\sigma _d^{\rm tot})W_{g,{\rm tot}}(\sigma _g)$ (Equation (41) or Equation (45)), as a function of the metallicity, assuming σ_g = 1.9 × 10⁻²¹Z' cm⁻² (ϕ_g = 1). The points are our numerical results, and the curve is our analytic fitting formula Equation (46). As expected, for low metallicity (full overlap) G∝Z', but for high metallicity G∝Z'^1/2 because of the H₂-dust cutoff. For Z' = 10, 1, 0.1, and 0.01, we find that G equals 1.3 × 10⁻⁴, 2.8 × 10⁻⁵, 5.4 × 10⁻⁶, and 7.1 × 10⁻⁷. For these metallicities, the average self-shielded dissociation rates are D₀G/2 = 3.8 × 10⁻¹⁵, 8.1 × 10⁻¹⁶, 1.6 × 10⁻¹⁶, and 2.1 × 10⁻¹⁷ s⁻¹. As discussed in Section 2.2.6 the average is over an H₂-dust optical depth τ₂ ∼ 1. For low metallicities, D₀G/2 becomes very small because the LW radiation is fully absorbed in lines at very low H₂-dust optical depths.

Zoom In Zoom Out Reset image size

We now present illustrative computations for the H i-to-H₂ transition profiles for a range of αG spanning the weak- to strong-field limits, and for metallicities Z' from high to low, for beamed and isotropic fields.

As discussed in Section 2.2.5, the profile shapes, i.e., the density ratios n₁/n and 2n₂/n as functions of the dust optical depth τ_g ≡ σ_gN (where N ≡ N₁ + 2N₂), depend on just the single dimensionless parameter αG ≡ D₀G/Rn. This includes the locations of the H i-to-H₂ transition points expressed in terms of τ_g. We define the transition point as the cloud depth where n₁/n = 2n₂/n = 0.5. For both beamed and isotropic fields we compute five transition profiles for αG/2 = 0.01, 0.1, 1, 10, and 10², for Z' = 1 and σ_g = 1.9 × 10⁻²¹ cm⁻² (ϕ_g = 1). These sequences illustrate the change in profile shapes, from "gradual" to "sharp," from the weak-field (H i-dust negligible) to strong-field limits (H i-dust dominant). In these computations G = 2.8 × 10⁻⁵ as appropriate for Z' = 1, and we set D₀ = 2 × 10⁻⁹ s⁻¹ (I_UV ≈ 35) and R = 3 × 10⁻¹⁷ cm³ s⁻¹ (T = 100 K). To alter α and αG, we vary n from 10 to 10⁵ cm⁻³.

For each αG/2 we plot the atomic and molecular fractions, n₁/n and 2n₂/n, as functions of the total (atomic plus molecular) column density, N. For fully atomic gas n₁/n = 1, and for fully molecular gas 2n₂/n = 1. For each model we also plot the normalized atomic column, ${\tilde{N}_1}\equiv N_1/N_{1,{\rm tot}}$, also as a function of N. Thus, ${\tilde{N}_1}\rightarrow 1$ at sufficiently large cloud depths where the LW radiation is fully absorbed. The curves for ${\tilde{N}_1}$ show how and where the atomic column is built up relative to the atomic-to-molecular transition points.

Figure 7, left panels, display the H i-to-H₂ transition profiles for the five beamed-field models with varying αG.

Zoom In Zoom Out Reset image size

Several important features can be seen in these plots. First, the atomic-to-molecular transition points move deeper into the cloud with increasing αG. For αG/2 = 0.01, 0.1, 1, 10, and 10², the total gas columns N_{1 → 2} at the transition points equal 5.6 × 10¹⁷, 1.4 × 10¹⁹, 3.0 × 10²⁰, 1.2 × 10²¹, and 2.4 × 10²¹ cm⁻². For the assumed σ_g = 1.9 × 10⁻²¹ cm⁻², these columns correspond to total dust optical depths τ_g = 1.05 × 10⁻³, 2.6 × 10⁻², 0.58, 2.3, and 4.5. The H i-dust optical depths at the transition points are 9.0 × 10⁻⁴, 2.0 × 10⁻², 0.45, 2.1, and 4.2. In the weak-field limit, the transition depths increase rapidly with αG. In the strong-field limit, the UV penetration is moderated by H i-dust absorption, and the transition depths increase slowly.

Second, the profile shapes vary with αG. In the weak-field limit, the atomic-to-molecular conversion is controlled by H₂-line self-shielding, but significant H i exists beyond the transition point up to the H₂-dust cutoff. In the weak-field limit, most of the H i column is built up past the transition point where the gas is predominantly molecular. In the strong-field limit, the transition point is controlled by (exponential) H i-dust absorption, and most of the H i is built up in an outer full atomic layer. Thus, in the weak-field limit the transitions are gradual, and in the strong-field limit the transitions are sharp. For example, at the H i-to-H₂ transition points, the normalized atomic column ${\tilde{N}_1}=0.08$, 0.19, 0.63, 0.85, and 0.92, from small to large αG. For αG/2 = 0.01, 92% of the total atomic column is built up past the transition point inside the molecular zone. For αG/2 = 100, only 8% of the atomic column is produced past the transition point.

Figure 7, right panels, show the transition profiles for isotropic fields for αG/2 ranging from 0.01 to 100, for Z' = 1 and σ_g = 1.9 × 10⁻²¹ cm². As for the beamed-field models, the shapes of the profiles vary from gradual to sharp from the weak- to strong-field limits. The transition gas columns are N_{1 → 2} = 3.7 × 10¹⁷, 8.4 × 10¹⁸, 1.6 × 10²⁰, 7.0 × 10²⁰, and 1.6 × 10²¹ cm⁻², or τ_g = 5.8 × 10⁻⁴, 1.6 × 10⁻², 0.30, 1.4, and 3.0. The normalized atomic columns at the transition points are ${\tilde{N}}_1=0.10$, 0.23, 0.59, 0.82, and 0.90. The H i-dust opacities are 5.8 × 10⁻⁴, 1.3 × 10⁻², 0.24, 1.2, and 2.8.

For fixed αG but varying Z' and σ_g, we expect the profile shapes to be invariant as functions of the dust optical depth τ_g, and we expect the UV penetration scale lengths and transition gas columns, N_{1 → 2}, to vary simply as 1/Z' or 1/σ_g. This behavior is illustrated in the upper panel of Figure 8 showing four transition profiles for Z' = 10, 1, 0.1, and 0.01 (again for beamed fields). For clarity we only plot the atomic n₁/n curves. For these models we set αG/2 = (αG)_CNM(Z')/2 = 1.11, 1.30, 1.28, and 1.12, as given by Equation (59) for self-regulated multiphased gas. Because αG is about the same for these models, the profile shapes are indeed very similar, and the transition columns grow inversely with Z'. For these four models, N_{1 → 2} = 3.0 × 10¹⁹, 3.7 × 10²⁰, 4.0 × 10²¹, and 4.2 × 10²² cm⁻², corresponding to dust opacities τ_g = 0.57, 0.70, 0.76, and 0.78. The H i-dust opacities at the transition points are 0.46, 0.56, 0.63, and 0.70. This behavior is in excellent agreement with the analytic theory presented in Section 2. For two-phased equilibrium, αG/2 ∼ 1 for all metallicities and is intermediate between the weak- and strong-field limits for which H i-dust opacity is just becoming significant.

Zoom In Zoom Out Reset image size

Figure 8, lower panel, shows the n₁/n curves for Z' = 10, 1, 0.1, and 1 for the isotropic-field models, with αG/2 = (αG)_CNM(Z')/2 as for the beamed-field models. Again, because αG is about the same for all four models, the profile shapes are very similar. The transition point columns are N_{1 → 2} = 1.6 × 10¹⁹, 1.9 × 10²⁰, 2.1 × 10²⁰, and 2.2 × 10²² cm⁻², or τ_g = 0.31, 0.36, 0.40, and 0.42. The H i-dust optical depths at the transition points are 0.25, 0.29, 0.33, and 0.37.

The transition columns and optical depths for all of the isotropic-field models are smaller than for the beamed-field models because of the factor-of-two reductions in the incident fluxes for corresponding isotropic fields with the same αG.

A key goal is the computation of the total atomic column densities, N_{1, tot}, for beamed and isotropic fields for a comparison with our analytic formulae.

In Figure 9, upper panel, we display N_{1, tot} for beamed fields, as a function of αG/2 spanning the range from 0.01 to 100, for Z' = 10, 1, 0.1, and 0.01.

Zoom In Zoom Out Reset image size

For our numerical models, we again set D₀ = 2 × 10⁻⁹ s⁻¹ and R = 3 × 10⁻¹⁷Z' cm³ s⁻¹ and vary the gas density n (to select α ≡ D₀/Rn), and we set σ_g = 1.9 × 10⁻²¹Z' cm². For the given input parameters D₀, R, n, and σ_g, we compute the total integrated atomic column density and also calculate W_{g, tot} and the associated average self-shielding factor $G=(\sigma _g/\sigma _d^{\rm tot})W_{g,{\rm tot}}$. For each model we compute N_{1, tot} for the corresponding αG and σ_g. The points in Figure 9 are our model results for selected αG and Z'. Again, for the four metallicities, G = 1.3 × 10⁻⁴, 2.8 × 10⁻⁵, 5.4 × 10⁻⁶, and 7.1 × 10⁻⁷. The curves in Figure 9 are as given by our fundamental analytic formula for beamed fields

$$\begin{equation} N_{1,{\rm tot}} = \frac{1}{\sigma _g}{\rm ln}\left[\frac{\alpha G}{2}+1\right], \end{equation} \tag{ 73 }$$

where 1/σ_g = 5.3 × 10²⁰/Z' cm⁻² as for the numerical models.

Our analytic and numerical results are in excellent agreement from the weak- to strong-field regimes. For weak fields (high gas densities), $N_{1,{\rm tot}}=(1/\sigma _g)\alpha G/2=(1/2){\bar{F}}_\nu W_{g,{\rm tot}}/Rn$ (Equation (52)). In this regime the total atomic column is proportional to the field intensity (dissociation flux) and varies inversely with the gas density. For strong fields (low densities), the dependence is logarithmic and N_{1, tot} = (1/σ_g)ln(αG) (Equation (54)). In this regime the atomic column is weakly dependent on I_UV/n, and it is limited to values close to 1/σ_g because of the dominating H i-dust absorption. For example, for Z' = 1 and αG/2 = 0.01, 0.1, 1, 10, and 100, our model computations give N_{1, tot} = 5.6 × 10¹⁸, 5.3 × 10¹⁹, 3.8 × 10²⁰, 1.2 × 10²¹, and 2.4 × 10²¹ cm⁻², as also given by our analytic formula.

Expressed as a function of αG, N_{1, tot}∝1/Z'. However, we recall that for large σ_g (Z' ≳ 1), αG is itself metallicity dependent and αG∝Z'^1/2 (see Equation (51)). Thus, for high metallicities in the weak-field limit, N_{1, tot}∝Z'^−3/2. In this regime the column decreases by one power of Z' because of enhanced H₂ formation efficiency and decreases by an additional factor of Z^1/2 because of the reduction of the effective dissociation flux by the H₂-dust. For low metallicities in the weak-field limit, the dissociation flux is maximal, and N_{1, tot}∝Z'⁻¹. In the strong-field limit, the atomic column is only weakly (logarithmically) dependent on αG, and the metallicity dependence is mainly via the H i-dust opacity, and N_{1, tot}∝Z'⁻¹ for all metallicities. These metallicity scalings, discussed in Section 2.2.8, are validated by our numerical model results for the atomic column.

In Figure 9 we also plot a (red) curve for (αG)_CNM(Z') as given by Equation (59) for self-regulated multiphased H i. As is again illustrated in Figure 9, (αG)_CNM(Z')/2 ∼ 1. Given the assumptions underlying Equation (59), the H i columns for self-regulated multiphased gas are intermediate between the linear (weak-field) and logarithmic (strong-field) regimes for all metallicities.

Our computational results show that our analytic expression for N_{1, tot} is valid for all transition profile shapes, whether gradual (weak fields) or sharp (strong fields), regardless of where the atomic column is built up (whether in the molecular zone or in the outer fully atomic layer). Indeed, in our analytic derivation we did not make any assumptions on the profile shape. Our expression is universal and valid for all regimes (weak and strong fields, high and low metallicities) and for all transition profile shapes (gradual or sharp). We emphasize this point again in our alternate derivation via the KMT/MK10 "transfer-dissociation equation" (Section 4.1.1).

In Figure 9, lower panel, we plot the total atomic columns for our isotropic-field models. For these models we select D₀ and R, and vary n to set α, and we compute the total H i column. As discussed in Section 3.2, the total dust-limited dissociation bandwidth, W_tot, and the average self-shielding factor, G, are identical for beamed and isotropic fields. In Figure 12 we plot N_{1, tot} as a function of αG, where for each Z' we use the G(Z') computed using beamed fields. Again, αG ranges from 0.01 to 100, and we present results for Z' from 10 to 0.01. The (αG)_CNM(Z') curve is also displayed. In Figure 9, the points are our numerical results, and the curves are as given by our fundamental analytic formula for isotropic fields (Section 2.3),

$$\begin{equation} N_{1,{\rm tot}} = \frac{\langle \mu \rangle }{\sigma _g} \ {\rm ln}\left[\frac{1}{\langle \mu \rangle }\frac{\alpha G}{4} \ + \ 1\right], \end{equation} \tag{ 74 }$$

where again 1/σ_g = 5.3 × 10²⁰/Z' cm⁻². To obtain the match between the numerical results and analytic formula shown in Figure 9, we have fit for the average angle factor 〈μ〉. We find that

$$\begin{equation} {\langle \mu \rangle } = 0.8 \end{equation} \tag{ 75 }$$

provides an excellent fit for all αG and for all σ_g∝Z'.

For isotropic fields in the weak-field limit, $N_{1,{\rm tot}}=(1/\sigma _g)\alpha G/4=(1/4){\bar{F}}_\nu W_{g,{\rm tot}}/Rn$ (Equation (68)). As discussed in Section 2.3, this is half the column for the corresponding beamed field because of the factor-of-two difference in the incident dissociation fluxes. For weak fields, N_{1, tot} is independent of 〈μ〉. In the strong-field limit, N_{1, tot} = (〈μ〉/σ_g)ln(αG/4〈μ〉) (Equation (69)), and the column is reduced by the factor 〈μ〉 = 0.8 compared with beamed-field models (neglecting the small difference in the logarithms). For example, for Z' = 1 and αG/2 = 0.01 0.1, 1, 10, and 100, our model results for the total atomic column are 3.1 × 10¹⁸, 2.9 × 10¹⁹, 2.1 × 10²⁰, 7.7 × 10²⁰, and 1.6 × 10²¹ cm⁻², smaller in the expected way compared with beamed-field models. The linear and logarithmic behaviors for small and large αG∝I_UV/n and the scaling with Z' are identical for isotropic and beamed fields.

Our expression for the total column for isotropic fields is also valid for all profile shapes, from gradual to sharp.

Let F_ν(z) be the flux density (photons cm⁻² s⁻¹ Hz⁻¹) at frequency ν of beamed LW radiation at linear depth z into a slab. The radiation flux (cm⁻² s⁻¹) between frequencies ν₁ and ν₂ is then

$$\begin{equation} F(z) \ \equiv \ \int _{{\nu _1}}^{{\nu _2}} F_{\nu }(z) \ d\nu. \end{equation} \tag{ 76 }$$

At the cloud surface F(0) = F₀/2, where F₀ is the flux integral (our Equation (3)) for the free-space radiation field.

The transfer equation for F(z) is

$$\begin{equation} \frac{dF}{dz} = -n\sigma _g F - n_2 \ \int _{{\nu _1}}^{{\nu _2}} \sigma _{\nu} F_\nu \ d\nu. \end{equation} \tag{ 77 }$$

Here n ≡ n₁ + 2n₂ is the total (atomic plus molecular) hydrogen gas volume density, and σ_ν is the ("complicated") cross section for the multiline H₂ absorption process.¹⁶ The first term on the right-hand side of Equation (77) is the dust absorption rate of the local radiative flux. The second term is the H₂-line absorption rate.

The steady state H₂ formation–destruction equation is

$$\begin{equation} Rnn_1 = {\bar{f}}_{\rm diss} n_2 \int _{{\nu _1}}^{{\nu _2}} \sigma _{\nu} F_\nu (z) \ d\nu, \end{equation} \tag{ 78 }$$

where in this expression, ${\bar{f}}_{\rm diss}$ (as defined in Section 2) is the mean fraction of all H₂-line absorptions that lead to photodissociation. Following Krumholz et al. (2008) and our discussion in Section 2, we assume that ${\bar{f}}_{\rm diss}$ is independent of cloud depth.

The "complicated" integral in Equation (77) may be eliminated to give the transfer-dissociation equation (Krumholz et al. 2008)

$$\begin{equation} \frac{dF}{dz} = -n\sigma _g F \ - \ \frac{Rnn_1}{{\bar{f}}_{\rm diss}}. \end{equation} \tag{ 79 }$$

In dimensionless form

$$\begin{equation} \frac{d {\cal F}}{d\tau } = -{\cal F} \ - \ \frac{2}{\chi }f_1, \end{equation} \tag{ 80 }$$

where ${\cal F}\equiv F/F(0)$ is the normalized depth-dependent flux, τ ≡ nσ_gz is the dust optical depth, and f₁(τ) ≡ n₁/n is the depth-dependent fraction of gas in atomic form.

In Equation (80)

$$\begin{equation} \chi \equiv \ \frac{{\bar{f}}_{\rm diss}\sigma _g F_0}{Rn}. \end{equation} \tag{ 81 }$$

This is the KMT/MK10 χ, here introduced for one-sided irradiation of a slab by a beamed field with incident LW flux F(0) ≡ F₀/2.¹⁷ Compared with our Equation (48) it is already clear that χ = αG for w = 1.

Because the product σ_gnF₀ is the dust absorption rate per unit volume of the surface LW radiation flux, and because $Rn^2f_1/{\bar{f}}_{\rm diss}$ is the H₂-line absorption rate per unit volume, KMT/MK10 interpret χ/f₁ as the ratio of the number of LW photons absorbed by dust to the number absorbed by H₂-lines at the optically thin cloud surface (with one factor of n canceling when doing the division). In this interpretation, the dust absorption being referred to in the numerator is independent of whether the gas is atomic or molecular.

However, as we now show, if the dust absorption term in the transfer-dissociation equation is redefined to refer to H i-dust absorption only, we will recover our fundamental formula for the H i column density, including a method for "renormalizing" the dissociation flux to account for H₂-dust absorption. We demonstrate this by analyzing the transfer-dissociation equation in the following three steps.

First, we assume—as done by KMT/MK10—that the atomic-to-molecular transition is always sharp. We impose this assumption even though we know that it is good only if our αG ≫ 1, i.e., only if F₀/n and χ are sufficiently large. Nevertheless, in seeking a solution for Equation (80), we assume that for any χ the atomic fraction f₁ = 1 everywhere ${\cal F}$ is non-zero, up to the (unknown) transition point where ${\cal F}$ vanishes. At that point the gas switches suddenly from H i to H₂.

Setting f₁ = 1, the solution to Equation (80) is

$$\begin{equation} {\cal F}(\tau) = \frac{\chi + 2}{\chi }{e}^{-\tau } \ - \ \frac{2}{\chi }. \end{equation} \tag{ 82 }$$

It is evident that the flux vanishes for τ = τ_{1, tot}, where

$$\begin{equation} \tau _{1,{\rm tot}} \equiv {\rm ln}\left[\frac{\chi }{2} + 1\right], \end{equation} \tag{ 83 }$$

and this is then the solution for the transition point (Krumholz et al. 2008). The total atomic column density up to the transition point is

$$\begin{equation} N_{1,{\rm tot}} = \frac{1}{\sigma _g}{\rm ln}\left[\frac{\chi }{2}+1\right], \end{equation} \tag{ 84 }$$

because by assumption there is no H₂ in the photodissociated layer and τ₁ is the optical depth due to H i-dust only.

We immediately recognize Equations (83) and (84). They are identical to our expressions (40) and (43) for the total H i-dust optical depth and H i column density, except that here the argument is χ, as given by Equation (81), rather than our αG as defined by the similar but not quite identical Equation (48). Indeed, it is apparent that αG = wχ, where w is the normalized effective dissociation bandwidth as defined by Equation (31). (This identity is clarified in Step 3.)

For χ ≫ 1, the attenuation of the LW flux is dominated by dust absorption, and ${\cal F}(\tau)\approx {e}^{-\tau }$. An exponentially attenuating flux is precisely what produces a sharp transition profile. Therefore, for χ ≫ 1 the assumption that the transition is sharp is consistent. Furthermore, the exponential attenuation is due specifically to H i-dust absorption. Sharp profiles occur when H i-dust dominates the attenuation.

For χ ≪ 1, dust absorption is negligible compared with H₂-lines, τ ≪ 1 throughout the atomic layer, and ${\cal F}(\tau)=1-2\tau /\chi$ to first-order in τ. For small χ, Equation (83) gives τ_{1, tot} = χ/2, so that

$$\begin{equation} N_{1,{\rm tot}} = \frac{1}{\sigma _g}\frac{\chi }{2} \end{equation} \tag{ 85 }$$

in this limit. However, when H₂-lines dominate the attenuation the transition is not sharp, and the assumption that f₁ = 1 is inconsistent.

Nevertheless, as we now show in Step 2, the above expressions for ${\cal F}(\tau)$, τ₁, and $N_1^{\rm tot}$ for large and small χ are valid for any varying f₁, whether or not the H i/H₂ transition is sharp, provided that H₂-dust is always negligible compared with H i-dust or H₂-lines, so that τ in Equation (80) can be redefined as the optical depth associated with H i-dust absorption only.¹⁸

With the neglect of H₂-dust absorption, Equation (79) is

$$\begin{equation} \frac{dF}{dz} = -n_1\sigma _g F \ - \ \frac{Rnn_1}{{\bar{f}}_{\rm diss}}, \end{equation} \tag{ 86 }$$

where now n has been replaced by n₁ in the first term on the right-hand side, or

$$\begin{equation} \frac{d{\cal F}}{d\tau } = -{\cal F} \ - \ \frac{2}{\chi }, \end{equation} \tag{ 87 }$$

where χ is again given by Equation (81) but where now

$$\begin{equation} \tau \equiv \sigma _g \ \int _0^z n_1 \ dz \ \ \ \end{equation} \tag{ 88 }$$

is defined in advance as the optical depth associated with H i-dust only.

In Equations (86) and (87), a factor f₁ ≡ n₁/n does not appear. The solutions are still given by Equations (84) and (85) for large and small χ but now with no assumptions on the shapes of the transition profiles.

For large χ the transition is sharp because the radiation flux is attenuated exponentially by the H i-dust, as shown in Step 1. However, for low χ, for which τ_{1, tot} is small, the transition need not be sharp. In this limit we again have,

$$\begin{equation} N_{1,{\rm tot}} = \frac{1}{\sigma _g}\frac{\chi }{2} = \frac{{\bar{f}}_{\rm diss}F_0/2}{Rn}. \end{equation} \tag{ 89 }$$

But this is just a Strömgren relation (as also noted by MK10). Therefore, it must hold independent of the shape of the H i/H₂ profile, provided only that the entire incident dissociation flux, ${\bar{f}}_{\rm diss}F_0/2$, is fully absorbed by H₂-lines, which it indeed will be for small τ_{1, tot}. Again, RnN_{1, tot} is the integrated H₂ formation rate per unit area, and in steady state this equals the fully absorbed dissociation flux ${\bar{f}}_{\rm diss}F_0/2$ impinging on the surface, independent of profile shape. In fact, we know that for low χ (i.e., for small F₀/n and αG) the transition profile is gradual, with most of the H i column built up in the molecular zone, as we have shown and discussed in Section 3.

Although Krumholz et al. (2008) derived their expression (83) for the dust optical depth assuming a sharp transition, it is actually valid for all χ, large and small, for sharp and gradual atomic hydrogen profiles, provided that H₂-dust absorption is negligible compared with H i-dust and H₂-lines.

We now include H₂-dust. In Equations (79) and (80), the original dust absorption term, nσ_gF, is not necessarily negligible—even when χ ≪ 1—if the atomic fraction f₁ is sufficiently small. This is the regime where H₂-dust absorption may be significant, even if H i-dust is negligible.

Because of H₂-dust absorption of radiation "between the lines," not all of the photons in the LW band are absorbed by the H₂, even for a fully molecular slab. The effective dissociation flux is then smaller than ${\bar{f}}_{\rm diss} F_0/2$. The Strömgren relation then implies that for χ ≪ 1 the total H i-dust optical depth τ_{1, tot} must be smaller than χ/2, rather than equal to χ/2 as given by Equation (89).

If τ is redefined to refer to H i-dust only as in Step 2, the effect of H₂-dust absorption can be included in the transfer-dissociation equation by a simple "renormalization" of the effective dissociation flux. We replace F₀/2 with a suitably reduced wF₀/2 equal to the flux of LW photons absorbed in H₂-lines in a dusty molecular slab, excluding in advance photons that are inevitably absorbed by H₂-dust. The renormalization factor can be computed in advance for any given σ_g, and we immediately recognize w as the (normalized) effective dissociation bandwidth that we defined and computed in Sections 2 and 3.

The transfer-dissociation equation for the renormalized LW flux is

$$\begin{equation} \frac{d(wF)}{dz} = -n_1\sigma _g wF - \frac{Rnn_1}{{\bar{f}}_{\rm diss}}, \end{equation} \tag{ 90 }$$

where again the dust term on the right-hand side refers to H i-dust absorption only. Photons absorbed by H₂-dust anywhere in the slab are excluded from consideration "in advance."

In dimensionless form

$$\begin{equation} \frac{d{\cal F}}{d\tau } = -{\cal F} - \frac{2}{\chi ^{\prime }}, \end{equation} \tag{ 91 }$$

where ${\cal F}\equiv F/F(0)$, dτ ≡ n₁σ_gz, and

$$\begin{equation} \chi ^{\prime } \ \equiv w\chi = \frac{{\bar{f}}_{\rm diss} \sigma _g wF_0}{Rn}. \end{equation} \tag{ 92 }$$

We see that χ' is just our αG (Equation (48)). Thus,

$$\begin{equation} \alpha G =w\chi \end{equation} \tag{ 93 }$$

as already indicated in Step 1.

Most importantly, in Equations (90) and (91) a factor "f₁" does not appear at all. The solution is

$$\begin{equation} {\cal F}(\tau) = \frac{\chi ^{\prime } + 2}{\chi ^{\prime }}{e}^{-\tau } \ - \ \frac{2}{\chi ^{\prime }}, \end{equation} \tag{ 94 }$$

where τ is the H i-dust optical depth, and there are no assumptions on the shape of the H i-to-H₂ transition profile. The flux vanishes for τ = τ₁, where

$$\begin{equation} \tau _{1, {\rm tot}} = {\rm ln}\left[\frac{\chi ^{\prime }}{2}+1\right] = {\rm ln}\left[\frac{\alpha G}{2} + 1\right], \end{equation} \tag{ 95 }$$

and the expression for the total atomic column is then

$$\begin{equation} N_{1, {\rm tot}} = \frac{1}{\sigma _g}{\rm ln}\left[\frac{\alpha G}{2} + 1\right]. \end{equation} \tag{ 96 }$$

We have thus recovered our original expressions (39) and (40) for the total atomic column and H i-dust opacity for beamed radiation into a slab. It is again clear that these expressions are general. They are valid for large or small αG (strong or weak fields) for the regimes of significant H i-dust and/or H₂-dust absorption and are independent of the profile shapes (gradual or sharp). We also have in Equation (94) a closed-form expression for the depth-dependent LW-band flux as a function of the H i-dust optical depth.

We again see that αG is the fundamental dimensionless parameter. Physically, αG is the ratio of the H i-dust to H₂-line absorption rates of the effective dissociation flux, excluding any LW photons that are absorbed by H₂-dust. The relationship between χ and our αG is now clear. Specifically, wχ ≡ αG, where crucially our factor w accounts for H₂-dust absorption and the resulting reduction of the effective dissociation flux. In the low-Z', small-σ_g limit, H₂-dust is negligible, w = 1, and χ = αG. For high Z' and large σ_g, w < 1 (decreasing as $\sigma _g^{-1/2}$ or as Z'^−1/2), and then αG < χ. KMT/MK10 did not make the distinction between H i-dust and H₂-dust and ignored the effects of H₂-dust entirely in their definition of χ. As we have discussed in Sections 2 and 3, H₂-dust can reduce the effective dissociation bandwidth by a factor ∼4 for the (realistic) range of metallicities in galaxies.

In Figure 10 we again schematically summarize the four regimes that are incorporated by our formula for the total H i column density. In each quadrant, large or small αG for large or small Z', we indicate the shape of the H i-to-H₂ transition (sharp or gradual), the dominant source of opacity (H i-dust, H₂-lines, or H₂-lines plus H₂-dust), and the expression for the H i-dust opacity in terms of the parameters σ_g, F₀, Rn, and w.

Zoom In Zoom Out Reset image size

Given our expressions (Equation (40) or Equation (65)) for the total H i-dust optical depths in semi-infinite slabs, we can write down a simple formula for the integrated H₂ mass fraction, $f_{{{\rm H}_2}}$, for planar geometry for a comparison with the KMT/MK10 results for spheres. Our main focus is a comparison of slabs and spheres irradiated by isotropic fields, but we also consider beamed radiation for slabs.

For an isotropic field with a given I_UV, a uniformly illuminated sphere corresponds to two-sided irradiation of a slab of finite width, with properly normalized total optical depths for the sphere and slab. For a slab with total dust thickness τ_z ≡ σ_gnz = σ_gN (where N is the total gas column density in the normal direction), the H₂ mass fraction is simply

$$\begin{equation} f_{{{\rm H}_2}}^{\rm p} = 1 - \frac{1}{y}, \end{equation} \tag{ 97 }$$

where y ≡ τ_z/τ₁, and τ₁ is the H i-dust depth summed over both sides of the slab (the superscript "p" indicates plane-parallel slab). By definition, y ⩾ 1. We plot $f_{{{\rm H}_2}}^{\rm p}$ versus y in Figure 11.

Zoom In Zoom Out Reset image size

For optically thick slabs in which the radiation incident on both sides is fully absorbed, and for illumination by isotropic fields, $\tau _1=\tau _1^{\rm p}$, where

$$\begin{equation} \tau _1^{\rm p} = 2\langle \mu \rangle \ {\rm ln}\left[\frac{1}{\langle \mu \rangle }\frac{\alpha G}{4} + 1\right] = 1.6 \ {\rm ln}\left[\frac{\alpha G}{3.2} + 1\right]. \end{equation} \tag{ 98 }$$

This is twice the optical depth given by our Equation (66) for one-sided illumination of a semi-infinite slab. (We have set 〈μ〉 = 0.8, as found in Section 3.) For beamed radiation $\tau _1=\tau _1^{\rm p,b}$, where

$$\begin{equation} \tau _1^{\rm p,b} = 2\ {\rm ln}\left[\frac{\alpha G}{2} + 1\right], \end{equation} \tag{ 99 }$$

given our Equation (39) for one-sided illumination (the superscript "b" is for beamed radiation). We plot $\tau _1^{\rm p}$ and $\tau _1^{\rm p,b}$ versus αG in Figure 12.

Zoom In Zoom Out Reset image size

For two-sided illumination of optically thick slabs, Equation (97) for $f_{{{\rm H}_2}}$ together with Equation (98) or Equation (99) for the total H i-dust optical depths may be used to compute the integral H₂ mass fractions whether the H i-to-H₂ transitions are gradual or sharp. For αG ≫ 1, an optically thick slab consists of a simple H i-H₂-H i sandwich structure, with two fully atomic layers outside an inner H₂ zone, with sharp transitions between the atomic and molecular layers. For sharp transitions a "critical" optically thick slab occurs for y = 1 for which an H₂ layer just appears at the midplane, and $\tau _1^{\rm p}$ or $\tau _1^{\rm p,b}$ are then the critical H i-dust optical depths. The planar sandwich for sharp transitions corresponds to the spherical core–shell structures considered by KMT/MK10, as illustrated in Figure 13.

Zoom In Zoom Out Reset image size

MK10 carried out their iterative radiative transfer procedure to compute spherical H i shell and H₂ core structures for two types of systems. First, they considered "uniform density" spheres for which the density of hydrogen nuclei, n = n₁ + 2n₂, is constant through the spheres as in our slabs. Second, they considered "atomic–molecular complexes" in which the H₂ gas density, n₂, is 10 times the atomic density, n₁, for approximate pressure equilibrium between the shells and the cores. MK10 then presented fitting formulae (their Equations (82) and (93)) for $f_{{{\rm H}_2}}$ in uniform density spheres and complexes, as functions of their cloud parameters χ and τ_r.

We can re-express the MK10 formulae for $f_{{{\rm H}_2}}$ as simple functions of y, similar to our Equation (97) for slabs. For spheres y ≡ 〈τ〉/〈τ₁〉, where 〈τ〉 ≡ σ_g〈N〉 is the area-averaged total dust column density of the sphere and where 〈N〉 ≡ M_gas/mπr² is the average gas column density, r is the cloud radius, and m is the mean particle mass per hydrogen nucleon. For a uniform density sphere, the total optical depth 〈τ〉 = 〈τ_r〉 ≡ (4/3)σ_gnr. For a complex, 〈τ〉 ⩾ (4/3)σ_gn₁r ≡ 〈τ_r〉, where n₁ is the gas density in the atomic shell. The parameter y is defined such that the total optical depth 〈τ〉 is normalized relative to the critical (area-averaged) dust depth 〈τ₁〉 required for the appearance of an H₂ core at r = 0. The critical depths 〈τ₁〉 are auxiliary quantities also computed by MK10 for the uniform density spheres and complexes, assuming irradiation by isotropic radiation fields. The 〈τ₁〉 for spheres correspond to our $\tau _1^{\rm p}$ for two-sided illumination of slabs by isotropic fields. In our terminology, these are the (total) H i-dust optical depths in spheres and slabs. For sharp transitions these are critical optical depths.

The MK10 fitting formula (their Equation (82)) for the H₂ mass fraction in uniform density spheres may be rewritten as¹⁹

$$\begin{equation} f_{{{\rm H}_2}}^{\rm s} \ \simeq \ 1 \ - \ \frac{1.5}{y + 0.5y^{-1.8}} \ \ \ \end{equation} \tag{ 100 }$$

(where the superscript "s" is for spheres). Their critical H i-dust optical depth is

$$\begin{equation} \langle \tau _1 \rangle = 1.1\times {\rm ln}[1 + 0.6\alpha G + 0.01(\alpha G)^2]. \end{equation} \tag{ 101 }$$

Again, in Equation (100) y ≡ 〈τ〉/〈τ₁〉. In Figures 11 and 12 we plot $f_{{{\rm H}_2}}^{\rm s}$ versus y and 〈τ₁〉 versus αG for comparisons with our expressions for slabs.

For complexes, the MK10 fit formula for the H₂ mass fraction (their Equation (93)) may be rewritten as²⁰

$$\begin{equation} f_{{{\rm H}_2}}^{\rm c} \ \simeq \ 1 - \frac{1.5}{y + 0.5}. \end{equation} \tag{ 102 }$$

(The superscript "c" is for complexes.) Fully atomic complexes and uniform density spheres are identical, so the critical H i-dust depth 〈τ₁〉 for complexes is also given by Equation (101). Because of the compression of the molecular gas, the functional form for $f_{{{\rm H}_2}}$ is altered compared with uniform density spheres, and the y^−1.8 factor in the denominator of Equation (100) is replaced by unity in Equation (102). We also plot $f_{{{\rm H}_2}}^{\rm c}$ for the complexes in Figure 11.

Figure 12 shows the similarity in the critical H i-dust optical depths for slabs and spheres. For isotropic fields, and for αG ranging from 0.01 to 10², the differences are no greater than 20%. Furthermore, Figure 12 shows that switching from isotropic to corresponding beamed radiation for a slab is in fact much more significant than switching from a slab to a sphere for an isotropic field. For isotropic fields, the H i-dust optical depths for slabs and complexes are equal for αG ≈ 1.5, so for two-phased H i equilibrium ([αG]_CNM/2 ∼ 1) the differences between the H i-dust optical depths for spheres and slabs are negligible. Thus, for αG ∼ 1 any differences between spheres and slabs arise only because of any remaining differences in the functional forms for $f_{{{\rm H}_2}}$.

Figure 11 shows the similarity and small differences in $f_{{{\rm H}_2}}$ for slabs, uniform-density spheres, and complexes, as given by Equations (97), (100), and (102). For slabs, our formula (97) for $f_{{{\rm H}_2}}$ is unaltered if the molecular gas is assumed to be denser than the atomic gas, and there is no distinction between uniform-density and isobaric conditions. The differences are all small. For example, for a spherical complex compared with a slab, the percentage difference in $f_{{{\rm H}_2}}(y)$ is at most 40% at y = 3.

If H₂ is a requirement for star formation, we may define the cloud gas column at which $f_{{{\rm H}_2}}=0.5$ as the "star-formation threshold." This is a plausible definition for sharp H i-to-H₂ transitions for which a "sterile" atomic layer is well defined. As given by Equations (97), (100), and (102), $f_{{{\rm H}_2}}=0.5$ for y = 2, 2.93, and 2.5, for slabs, uniform density spheres, and complexes. We define Σ_{gas, *} as the threshold gas mass surface density for which $f_{{{\rm H}_2}}=0.5$.

For estimates of metallicity-dependent H₂ mass fractions and star-formation thresholds in Kennicutt–Schmidt relations for galaxy disks, we adopt the KMT/MK10 "self-regulation" ansatz that the H i in star-forming clouds is typically driven to the CNM densities/pressures required for two-phase equilibria as set by the stellar FUV radiation fields. Thus, for any Z' we assume that αG = (αG)_CNM(Z') (Equation (59)). Because (αG)_CNM ∼ 1 to 2 for all Z', the H i-to-H₂ transitions are sharp to a good approximation (as argued by KMT/MK10). For our slabs we therefore assume H i-H₂-H i sandwich structures, for which critical optically thick slabs occur at y = 1 (as discussed in Section 4.2.1).

We present four sets of computations to compare results for spheres versus slabs.

First, in Figure 14, panel (a), we use Equations (102) and (101) to reproduce the MK10 results for $f_{{{\rm H}_2}}^{\rm c}(\Sigma _{{\rm gas}})$ for spherical atomic–molecular complexes (Figure 5 in MK10). Here Σ_gas ≡ (m/σ_g)〈τ〉 is the area-averaged gas mass surface density, where m is the mean particle mass per hydrogen nucleus and 〈τ〉 is the area-averaged dust opacity. Thus, in Equation (102) y = Σ_gas/Σ₁, where Σ₁ ≡ (m/σ_g)〈τ₁〉, and where 〈τ₁〉 is given by Equation (101) for each (αG)_CNM(Z'). We set m = 2.34 × 10⁻²⁴ g as appropriate for a cosmic hydrogen–helium mixture. KMT/MK10 assume that the dust cross section scales with metallicity as σ_g = 1.0 × 10⁻²¹Z' cm², so we set our ϕ_g = 1/1.9 (see Equation (20)). MK10 also implicitly assume that H₂-dust absorption is negligible for all Z', so we exclude our H₂-dust term, (2.64ϕ_gZ')^1/2, in the denominator of Equation (59). The resulting curves for $f_{{{\rm H}_2}}$ as functions of Σ_gas (M_☉ pc⁻²) are displayed in Figure 14 for Z' ranging from 0.01 to 10. They are a precise reproduction of the MK10 results (their Figure 5). For example, with the above assumptions, Z' = 1 gives (αG)_CNM = 3.6 so that 〈τ₁〉 = 1.3, and a molecular core appears (y = 1) for Σ_gas = 14.6 M_☉ pc⁻². The $f_{{{\rm H}_2}}^{\rm c}=0.5$ star-formation threshold (y = 2.5) is then Σ_{gas, *} = 36.5 M_☉ pc⁻². For smaller (larger) Z', the curves shift to the right (left) exactly as in Figure 5 of MK10.

Zoom In Zoom Out Reset image size

Second, in Figure 14, panel (b), we show results for spherical complexes, again with ϕ_g = 1/1.9 but now with the H₂-dust term included in the estimate for (αG)_CNM(Z'). As expected, for very low Z' the $f_{{{\rm H}_2}}$ curves and the corresponding star-formation thresholds are unaltered, since this is the complete line overlap regime for which H₂-dust is negligible. However, for Z' ≳ 0.3 the curves start to shift to the left and the thresholds are reduced to smaller gas mass surface densities. These shifts are due to the reductions of the effective dissociation fluxes by the non-negligible H₂-dust opacities. For example, when H₂-dust is included for Z' = 1 we have (αG)_CNM = 1.6 (for ϕ_g = 1/1.9) so that 〈τ₁〉 = 0.77, and the H₂ core appears at Σ_gas ≃ 8.6 M_☉ pc⁻² and Σ_{gas, *} = 21.5 M_☉ pc⁻². The inclusion of H₂-dust in the estimate for (αG)_CNM modifies the MK10 results for solar and super-solar metallicities.

Third, in Figure 14, panel (c), we again adopt the MK10 assumptions, ϕ_g = 1/1.9 and negligible H₂-dust for any Z' but for slabs instead of spheres, and we use Equation (97) to compute $f_{{{\rm H}_2}}^{\rm p}(\Sigma _{{\rm gas}})$. Here Σ_gas = (m/σ_g)τ_z, where τ_z is the total dust depth of the slab, so that y = Σ_gas/Σ₁ where $\Sigma _1=(m/\sigma _g) \tau _1^{\rm p}$, and the critical H i-dust optical depth $\tau _1^{\rm p}$ is given by Equation (98) for each (αG)_CNM(Z'). We have already seen that the functional forms for the mass fractions are very similar for complexes and slabs (with at most a 40% difference at y = 3) and that the critical H i-dust columns are essentially equal for αG ∼ 1 (as for self-regulated gas). It is therefore not surprising that the curves for slabs are almost identical to the MK10 results in Figure 14. For Z' = 1, we again have (αG)_CNM = 3.6 so that $\tau _1^{\rm p}=1.2$ and H₂ appears for Σ_gas ≃ 13.4 M_☉ pc⁻² and the star-formation threshold (y = 2) is at Σ_{gas, *} = 26.8 M_☉ pc⁻². For metallicities Z' ≳ 0.3, the neglect of H₂-dust in setting (αG)_CNM is more significant than switching from spherical to plane-parallel cloud geometry.

In Figure 14, panel (d), we again present results for slabs but now with our preferred and somewhat larger σ_g = 1.9 × 10⁻²¹Z' cm² (ϕ_g = 1) and with the inclusion of H₂-dust absorption in setting (αG)_CNM(Z'). The $f_{{{\rm H}_2}}^{\rm p}$ curves and thresholds are shifted to lower gas mass surface densities compared to Figure 14. For Z' = 1, we now have (αG)_CNM = 2.6, given that $\tau _1^{\rm p}=0.95$, so that H₂ appears at Σ_gas = 5.6M_☉ pc⁻² and the star-formation threshold surface gas mass density is Σ_{gas, *} = 11 M_☉ pc⁻².

Finally, in Figure 15 we plot Σ_{gas, *}(Z') for the above four model sets. At any Z' the star-formation thresholds vary by factors of 2–3 for the four model assumptions, for Z' between 0.01 and ∼2. Again, we are assuming that αG = (αG)_CNM(Z') for which the critical H i-dust optical depths are all of order unity. The threshold gas mass surface densities therefore scale as ∼2m/σ_g, and we have

$$\begin{equation} \Sigma _{{\rm gas},*}(Z^{\prime }) \ \approx \ \frac{12}{\phi _g Z^{\prime }} \ \ \ {M}_\odot \ {\rm pc}^{-2}. \end{equation} \tag{ 103 }$$

For Z' ∼ 1, the star-formation thresholds are of order 10 M_☉ pc⁻².

Zoom In Zoom Out Reset image size

The predicted H i columns and star-formation thresholds appear consistent with observations, at least for ∼solar metallicity systems. For example, in a recent GALFA-H i study of the H i-to-H₂ transition on sub-parsec scales in the Perseus giant molecular cloud, Lee et al. (2012) find an almost constant H i surface density of $\Sigma _{{\rm H}\,\scriptsize{I}}\sim 6\hbox{--}8$ M_☉ pc⁻² in each of the mapped sub-regions. For Z' = 1, this is consistent with the H i columns expected for αG of order unity, including conditions appropriate for two-phased equilibrium. Thus, Perseus is in the H i-dust-limited and strong-field regime. On larger scales, Leroy et al. (2008) find a mean total gas column of 14 M_☉ pc⁻² at the H i-to-H₂ transition radii (see their Table 5) in their analysis of the H i and CO distributions in the THINGS and HERACLES galaxy surveys. The observed threshold column density of 14 M_☉ pc⁻² is in harmony with our 1D predictions or the spherical KMT/MK10 models (see Figure 15). However, in this interpretation there must be typically one primary UV absorbing cloud (GMC) per line of sight in the galaxy surveys, with negligible additional diffuse H i, since our predicted thresholds are for single cold clouds.