ABSTRACT
We present an analytical model that describes the evolution of two consecutive interplanetary coronal mass ejections (ICMEs), their interaction, and the evolution of the merged region. In this model, the coronal mass ejections (CMEs) are seen as velocity and density (mass loss rate) fluctuations of the solar wind that result in the formation of shocks traveling into the ambient solar wind (ASW). The dynamical evolution of these structures depends on both the CME parameters such as the initial velocity, density, and the duration of the eruption as well as the solar wind conditions (ejection velocity and mass loss rate). The probability of an interaction of two consecutive CMEs launched in the same direction is high, basically depending on their speeds and the interval of time between the CMEs. As a result of the interaction, a merged region is formed. Its dynamical evolution is also addressed by the present model. Given a set of initial CMEs and ASW conditions, our model is able to predict the time and distance of the interaction between the ICMEs and the velocity of the merged region as a function of the heliospheric distance. These are fundamental parameters of space weather predictions. Also, the model is able to predict the arrival time and velocity of the merged region at 1 AU. In this work, we validate the model through its application to well documented interaction events observed on 2007 January 24, 2010 May 23, 2010 August 01, and 2012 November 09.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
A coronal mass ejection (CME) is an excess of mass and magnetic field expelled from the low solar atmosphere into the interplanetary medium with velocities ranging from ∼100 up to ∼3000 km s−1. In interplanetary space (above ∼15 solar radii), the CMEs are called interplanetary coronal mass ejections (ICMEs) and their dynamics are determined by their interactions with the ambient solar wind (ASW; Cantó et al. 2005; Borgazzi et al. 2009; Lara et al. 2011) and other large-scale structures such as corotating interaction regions (CIRs) or other ICMEs (Gopalswamy et al. 2001a). During these interactions, there is an interchange of momentum between the colliding structures and a complex region is formed (Gopalswamy et al. 2001b; Burlaga et al. 2002).
Observationally, the study of the interaction of two consecutive ICMEs is based on coronagraph images, in situ measurements, and radio signatures. Recently SECCHI (Howard et al. 2008), on board the STEREO spacecraft (Kaiser et al. 2008), has made possible to track the density enhancements associated with ICMEs, from low corona to 1 AU, and their interactions. From a theoretical point of view, numerical simulations have been developed to study these interactions (Vandas et al. 1997; Schmidt & Cargill 2004; Lugaz et al. 2005; Xiong et al. 2006), giving us a global view of the process.
On the other hand, analytical models help us to understand the dynamics of the interactions of ICMEs with the ASW (Cantó et al. 2005; Borgazzi et al. 2009; Vršnak et al. 2010, 2013). In this direction, Cantó et al. (2005) developed an analytical model to give insights into the physics of isolated ICME propagation. In this model, a CME is initiated as a perturbation ejected from the Sun into the smooth and steady solar wind. The perturbation is such that the velocity and density suddenly change during a certain interval of time (the duration of the CME). These abrupt changes form a "working surface" (WS) at the interface between the ASW and the ICME material. The WS is bounded by two shock fronts: the inner (or reverse) shock, which decelerates the fast ICME material, and the outer (leading) shock, which accelerates the ASW (see also Raga et al. 1990).
In our approximation to ICME macroscopic dynamics, we assume that the kinetic energy of the plasma is much higher, and therefore dominates over the magnetic field energy (see Borgazzi et al. 2009 for an approximate quantification). The validity of this assumption is supported by the fact that our model of ICME interactions, as well as other models of transports of ICMEs based in hydrodynamics, reproduce very well the observed behavior of ICMEs (Cantó et al. 2005; Borgazzi et al. 2009; Vršnak et al. 2010, 2013). The magnetic field interactions are important at microscopic scales through wave–particle interactions (e.g., Subramanian et al. 2012).
We agree that the internal magnetic field should play an important role in the internal evolution of the merged region, but the collision distance and time are independent of the internal magnetic field of the individual CMEs. After the collision, the merged region is regarded as a new working surface with no internal structure. This is a limitation of the model.
In the present work, we expand the model of Cantó et al. (2005) to study the evolution, propagation, and interaction of two consecutive ICMEs, as well as the dynamics of the resultant merged region. We present the formalism of the model in Section 2. In Section 3, we validate our model by applying it to a set of well documented events of ICME interactions observed on 2007 January 24 (Lugaz et al. 2008, 2009), 2010 May 23 (Lugaz et al. 2012), 2010 August 01 (Temmer et al. 2012), and 2012 November 09 (Mishra et al. 2014). Finally, our discussion and conclusions are presented in Section 4.
2. THE MODEL
In this model, the solar wind is treated as a steady flow of particles going out of the Sun and a CME is characterized by an increase in the velocity and density of this flow. The change of these parameters is defined by the constant ratios  and
and  where v0 and
where v0 and  are the velocity and density of the ASW, respectively. The change of the mass-loss rate is characterized by the factor
are the velocity and density of the ASW, respectively. The change of the mass-loss rate is characterized by the factor  (note that
(note that  due to the continuity equation). After a finite interval of time,
due to the continuity equation). After a finite interval of time,  determined by the duration of the eruption, the flow parameters return to their original values. The initial jump of the flow parameters causes the formation of a two-shock structure called working surface WS (Raga et al. 1990; Cantó et al. 2005).
determined by the duration of the eruption, the flow parameters return to their original values. The initial jump of the flow parameters causes the formation of a two-shock structure called working surface WS (Raga et al. 1990; Cantó et al. 2005).
In this work, the ICME dynamic is then represented by the evolution of the WSs. Studying the formation, evolution, and collision of the WSs associated with two consecutive ICMEs, we are able to determine the behavior of the system: the individual ICMEs and the merged region formed after the collision. In Figure 1, we present a schematic diagram of the system before the collision.
Figure 1. Schematic diagram showing the flow pattern after two velocity fluctuations. The material of ICME1 moves with constant velocity  while ICME2 moves with constant velocity
while ICME2 moves with constant velocity  . Both ICMEs interact with the ASW of velocity v0 and produce working surfaces WS1 and WS2, respectively. The working surfaces are bounded by two shock fronts. In this work, we assume that
. Both ICMEs interact with the ASW of velocity v0 and produce working surfaces WS1 and WS2, respectively. The working surfaces are bounded by two shock fronts. In this work, we assume that  , therefore gaps are developed behind ICME1 and ICME2.
, therefore gaps are developed behind ICME1 and ICME2.
Download figure:
Standard image High-resolution imageThe WSs form at the instant when the CMEs are expelled outward from the Sun. Afterward, each WS travels downstream of the ASW flow, and at given time t, the WS is located at a distance xs from the injection source. This distance must coincide with the position of the center of mass of the WS, which is given by
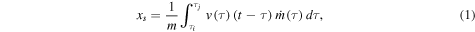
where m is the mass acumulated inside the WS,

 and
and  are the initial velocity and mass-loss rate of the flow that is incorporated into the WS, τ is the injection time of the flows, and
are the initial velocity and mass-loss rate of the flow that is incorporated into the WS, τ is the injection time of the flows, and  and
and  are the injection times directly upstream and downstream of the WS at a time t, respectively (Cantó et al. 2000).
are the injection times directly upstream and downstream of the WS at a time t, respectively (Cantó et al. 2000).
We define a function F as
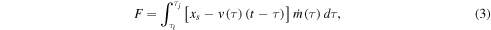
which, by Equations (1) and (2), must equal zero during the evolution of the WS. That is,
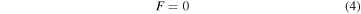
for any time t.
By using the free-streaming approximation for the flow and assuming that the width of the WS is negligible (thin layer approximation) we also have
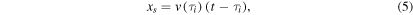
and
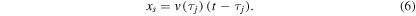
Equations (4)–(6) relate our four unknown variables: xs, t,  , and
, and  Thus, we can find three of them in terms of the fourth.
Thus, we can find three of them in terms of the fourth.
Using this model, we are able to study the dynamical evolution of any ICMEs and, in the case of two or more consecutive ICMEs, this model predicts the time of the interaction as well as the position and the velocity of the merged region at any time.
In this work, we present the solution of the model applied to the interaction of two consecutive ICMEs. A qualitative plot of the flow properties as a function of the injection time τ is shown in Figure 2. For the sake of simplicity, in this work we assume that the ASW has the same parameters before, between, and after the CMEs (see Figure 2), though this condition can be changed.
Figure 2. Schematic diagram of the outflow velocity as function of the injection time τ. The ICME1 material moves with a constant velocity  starting at a time
starting at a time  and lasting
and lasting  . The Sun again blows out the ASW during an interval of time
. The Sun again blows out the ASW during an interval of time  , then at a time
, then at a time  ,
,  is expelled outward from the Sun with constant velocity
is expelled outward from the Sun with constant velocity  during an interval of time
during an interval of time  .
.
Download figure:
Standard image High-resolution imageWe would like to note that the model can be expanded to any number of CMEs traveling into the ASW. The model is able to predict the time of the different interactions and the evolution of the resultant merged region(s) at any distance from the Sun. The major assumption is that CME dynamics are dominated by the kinetic energy of the plasma, and therefore the magnetic energy can be neglected.
2.1. Leading ICME
Before the CME launch, at quiet times, the Sun blows out a stationary wind with velocity v0, density  , and mass-loss rate
, and mass-loss rate  for injection times
for injection times  Then, at
Then, at  the first perturbation (CME1) starts flowing with velocity
the first perturbation (CME1) starts flowing with velocity  density
density  , and mass-loss rate
, and mass-loss rate  lasting for a time interval
lasting for a time interval  (Figure 2). Following the formalism of Cantó et al. (2000; see also González & Cantó 2002; Cantó et al. 2005), it can be shown that the first WS1 is instantaneously formed when the jump of the flow parameters occurs. Then, the dynamical evolution of the shocked material depends on the jump factors a1, b1, and
(Figure 2). Following the formalism of Cantó et al. (2000; see also González & Cantó 2002; Cantó et al. 2005), it can be shown that the first WS1 is instantaneously formed when the jump of the flow parameters occurs. Then, the dynamical evolution of the shocked material depends on the jump factors a1, b1, and  The evolution of the WS1 comprises two phases, A1 and B1.
The evolution of the WS1 comprises two phases, A1 and B1.
2.1.1. Phase A1
The initial phase A1 is characterized by a constant velocity with an intermediate value between the ASW and the CME1 velocities. This is due to the fact that both flows are transferring momentum to the WS1 at constant rates. Therefore, the initial velocity of the WS1 depends on the interplay between the momentum injected into the WS1 by both the CME1 and the ambient wind ahead.
To solve this phase, we find the function F (see Equation (3) and Figure 2);
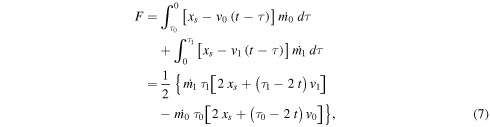
where the first integral is related to the ASW in front of the WS1 (with 
 and
and  ), while the second integral corresponds to the CME1 behind of the WS1 (with
), while the second integral corresponds to the CME1 behind of the WS1 (with  and
and  and
and  ),
),
Using the condition F = 0 (see Equation (4)) and the free-streaming conditions (see Equations (5) and (6)),
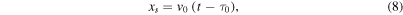
and
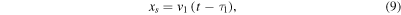
for this phase, we find,
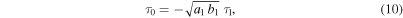

and,
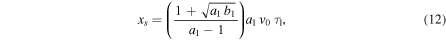
where we have used  as a free parameter.
as a free parameter.
From Equations (11) and (12) it follows that the WS1 moves with a constant velocity given by
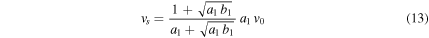
during this initial phase. Thus, we may write from Equations (11) to (13),  with vs given by Equation (13).
with vs given by Equation (13).
This phase of constant velocity ends when all the mass and momentum of CME1 have been transferred to WS1, that is, when  Applying this condition to Equations (11) and (12), we find the final time,
Applying this condition to Equations (11) and (12), we find the final time,
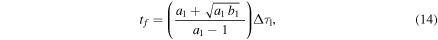
and the distance,
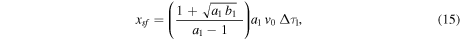
for this initial, constant velocity phase. After this point, the inner shock disappears and only the ASW feeds the working surface with low velocity material, and the WS1 enters into a new, decelerated, phase B1.
2.1.2. Phase B1
In this second phase, the function F (see Equation (3)) is given by
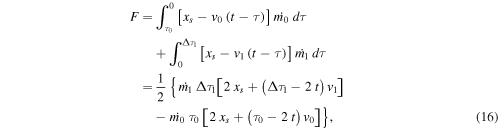
where the second integral is limited by the duration of CME1, 
Using the condition F = 0 and the free-streaming Equation (8) we obtain

where the free parameter is now  The position of WS1 in this second stage (B1) is obtained by substituting Equation (17) into (8), that is,
The position of WS1 in this second stage (B1) is obtained by substituting Equation (17) into (8), that is,
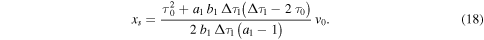
The velocity of WS1 in this second stage is given by

in terms of the parameter  This velocity steadily decreases from the value at stage A1 (given by Equation (13)), approaching asymptotically the velocity v0 of the ASW, for
This velocity steadily decreases from the value at stage A1 (given by Equation (13)), approaching asymptotically the velocity v0 of the ASW, for 
As expected, Equations (17)–(19) exactly match Equations (11)–(13), respectively, when  that is, at time tf and distance xsf (Equations (14) and (15), respectively).
that is, at time tf and distance xsf (Equations (14) and (15), respectively).
2.2. Trailing ICME
When CME1 ends, the ASW is blown out again during an interval of time  (between
(between  and
and  see Figure 2). For simplicity, we have assumed that the parameters of the new ASW are exactly the same than those of the ASW before the first eruption (v0,
see Figure 2). For simplicity, we have assumed that the parameters of the new ASW are exactly the same than those of the ASW before the first eruption (v0,  and
and  ). This assumption is not necessary.
). This assumption is not necessary.
At time  a second perturbation (CME2) is expelled from the Sun with velocity
a second perturbation (CME2) is expelled from the Sun with velocity  mass-loss rate
mass-loss rate  and density
and density  (
( ) during a finite interval of time
) during a finite interval of time  (see Figure 2). At the time when CME2 is launched, a new WS2 is formed, and its dynamical evolution depends on the jump factors a2 (
(see Figure 2). At the time when CME2 is launched, a new WS2 is formed, and its dynamical evolution depends on the jump factors a2 ( ), b2, and c2, and the duration of CME2,
), b2, and c2, and the duration of CME2,  Its evolution comprises three phases: an initial phase A2 of constant velocity, a second phase B2 of acceleration/deceleration, and a third phase C2 of constant velocity.
Its evolution comprises three phases: an initial phase A2 of constant velocity, a second phase B2 of acceleration/deceleration, and a third phase C2 of constant velocity.
2.2.1. Phase A2
During the initial phase of constant velocity of the trailing WS2, the function F is given by
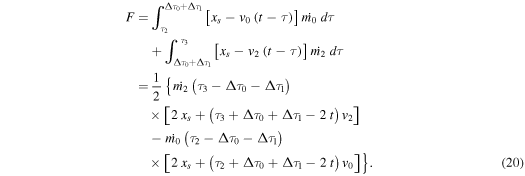
The result is, of course, the same as that given by Equation (7), but shifted in time by  Using, again, the free-streaming Equations (5) and (6) in the form
Using, again, the free-streaming Equations (5) and (6) in the form
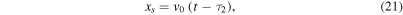
and
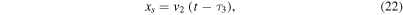
together with the condition F = 0 in Equation (20), we find,
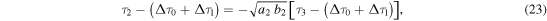
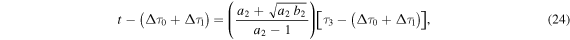
and
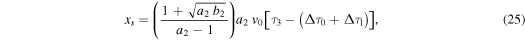
which are equivalent to Equations (10)–(12), but shifted in time by 
Since the material of the ASW and ICME2 are incorporated into the WS2 at constant rates, the WS2 moves with a constant velocity,
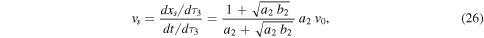
which is, of course, similar to Equation (13), but for a2 and b2.
This phase of constant velocity lasts until either the ICME2 or ASW material is completely incorporated into WS2, and a new accelerated/decelerated phase B2 begins.
2.2.2. Phase B2
If the ICME2 material runs out first, then the WS2 starts a deceleration phase, because it only sweeps the lower velocity material of the ASW in front of it. On the other hand, if the ASW is incorporated completely into the WS2 first, then the WS2 is accelerated by the fast ICME2 material, which is still being incorporated into the WS2.
It can be shown that both ICME2 and the ASW run out at the same time for

Thus, if  , then the ASW runs out first and the WS2 is accelerated by the incorporation of the fast ICME2 material, while if
, then the ASW runs out first and the WS2 is accelerated by the incorporation of the fast ICME2 material, while if  , the ICME2 material runs out first and then the WS2 is decelerated by the incorporation of the slow ASW in front of it.
, the ICME2 material runs out first and then the WS2 is decelerated by the incorporation of the slow ASW in front of it.
2.2.2.1. Phase B2—Decelerated
Let us first consider the decelerated case ( ). This second phase begins when
). This second phase begins when  at a time (Equation (24)),
at a time (Equation (24)),
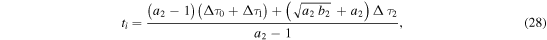
when the working surface is at the distance (Equation (25)),
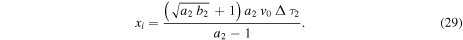
and  from Equation (23).
from Equation (23).
During this second phase of deceleration the function F is
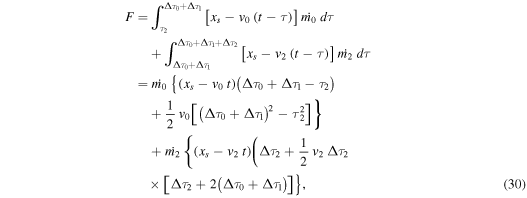
where  is now the free parameter.
is now the free parameter.
Using the condition F = 0, and the free-streaming equation,

we find
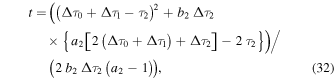
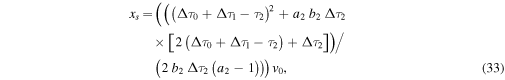
and
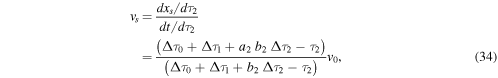
in terms of the free parameter 
This phase ends when all of the ASW material has been incorporated into the WS2, i.e., when  (see Figure 2). Using this condition, in Equations (32)–(34) we have the time, position, and velocity of the WS2 at the end of this decelerated phase. They are
(see Figure 2). Using this condition, in Equations (32)–(34) we have the time, position, and velocity of the WS2 at the end of this decelerated phase. They are
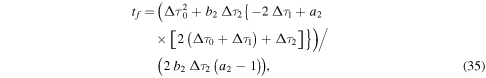
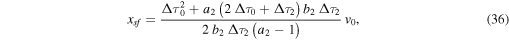
and

Afterward, the WS2 moves with a constant velocity given by Equation (37) (see Section 2.2.3)
2.2.2.2. Phase B2—Accelerated
On the other hand, if  the WS2 is accelerated, since the fast ICME2 material is incorporated into the WS2. The acceleration phase of the WS2 starts at the distance,
the WS2 is accelerated, since the fast ICME2 material is incorporated into the WS2. The acceleration phase of the WS2 starts at the distance,
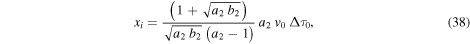
and at a time
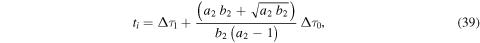
which follow from Equations (23) to (25) with 
In this phase, the function F is
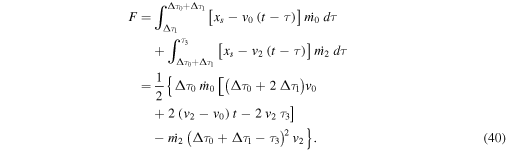
From the condition F = 0 and the free-streaming function,
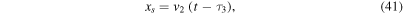
we find,
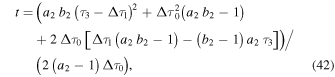
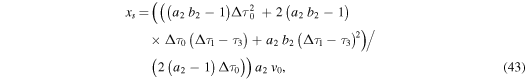
and
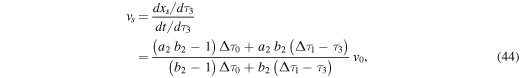
as a function of the free parameter 
This phase of acceleration ends when all the momenta of the ICME2 and the ASW have been transferred to the WS2, that is, when  This occurs at the time,
This occurs at the time,

and at the distance from the Sun,
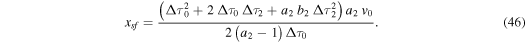
Afterward, the WS2 moves with constant velocity,
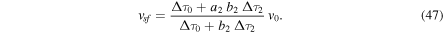
Equations (45)–(47) follow directly from Equations (42) to (44) with 
2.2.3. Phase C2
At the end of the accelerated/decelerated B2 phase, the WS2 moves with a velocity given by either Equation (37) or Equation (47), which are the same equation. These equations are the same because they are given by conservation of momentum: in Equation (37) or (47), the numerator represents the sum of the total momenta of the ASW ( ) and the ICME2 (
) and the ICME2 ( ); while the denominator is the sum of their masses (
); while the denominator is the sum of their masses ( ) and (
) and ( ), respectively. Their ratio is the velocity of the WS2. This velocity is constant during this phase. Thus, the position of the WS2 at time t is,
), respectively. Their ratio is the velocity of the WS2. This velocity is constant during this phase. Thus, the position of the WS2 at time t is,
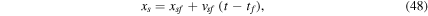
where tf, xsf, and vsf are given by the set of Equations (35)–(37) if the WS2 was decelerated or the set of Equations (45)–(47) if the WS2 was accelerated during the previous phase B2.
2.3. Merged Region
When the fast WS2 reaches the slower WS1, they collide and form a merged region. Due to the conservation of momentum, this merged region travels initially with an intermediate velocity between the velocities that WS1 and WS2 had just before the collision.
The time and distance of the collision depends on the initial parameters of the individual events. The collision occurs when all the mass between the two WSs has been completely incorporated. Consequently, the WS1 is in its decelerated phase B1 and the WS2 may be in either: (i) its final phase of constant velocity, (ii) its accelerated phase, or (iii) its decelerated phase. As an example of the formalism of the model, we present below the detailed solution for the first two cases which are related to events described in Section 3.
Case (i) In three of the events (2007 January 24, 2010 May 23 and 2012 November 09), the WSs collide when the WS1 is in a decelerated phase B1 while the WS2 is in phase C2.
From substitution of the Equations (17) and (18) into the Equation (48), we find the value of  at the instant of collision (
at the instant of collision ( ). Then, we evaluate the Equations (17) and (18) at
). Then, we evaluate the Equations (17) and (18) at  to find the time and distance of the collision.
to find the time and distance of the collision.
After this point ( ), the dynamics of the merged WS is described by the function F,
), the dynamics of the merged WS is described by the function F,
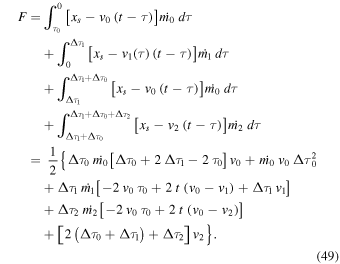
From the condition F = 0 and the free-streaming equation,
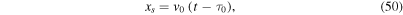
we find the solution
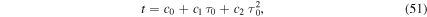

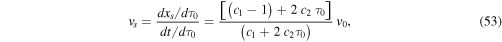
where
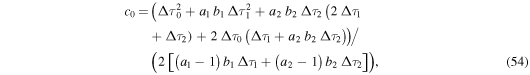
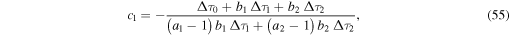
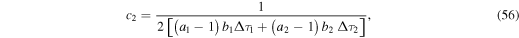
in terms of the free parameter 
Case (ii): For the event of 2010 August 01 (see Section 3), the collision took place when the WS1 was in its decelerated phase B1, while the WS2 was in its accelerated phase B2. The time and distance of collision are thus found by solving simultaneously Equations (17) and (18) and Equations (42) and (43). First, we determine the values of  and
and  when the collision occurred (
when the collision occurred ( and
and  ) and then, we determine the values of t and xs at that moment. After this point (
) and then, we determine the values of t and xs at that moment. After this point ( and
and  ), the further dynamical behavior of the merged WS is described by the function F,
), the further dynamical behavior of the merged WS is described by the function F,
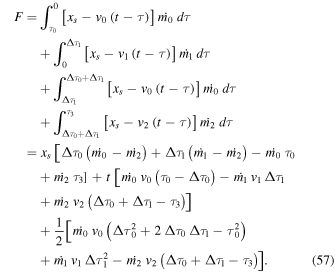
Using the free-streaming equations,
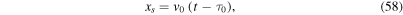
and
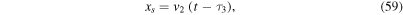
in Equation (57) we find
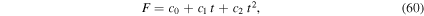
where
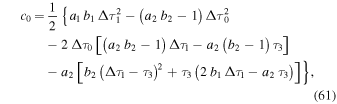
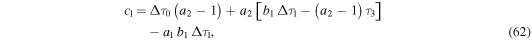
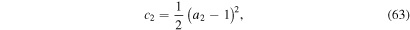
in terms of the free parameter 
From the condition F = 0 we then find
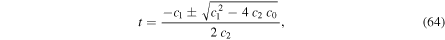
and
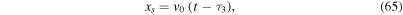
with  the free parameter. The sign in Equation (64) is determined by the initial conditions of the collision. During this phase, the velocity of the merged WS can be found from Equation (65),
the free parameter. The sign in Equation (64) is determined by the initial conditions of the collision. During this phase, the velocity of the merged WS can be found from Equation (65),
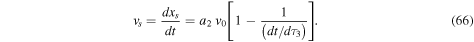
From Equation (60) and the condition F = 0,
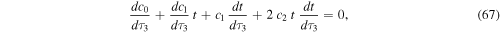
thus,
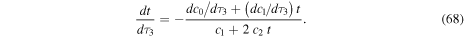
Substituting Equation (68) in (66) we find:
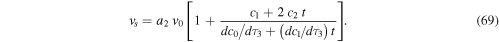
Using Equations (61)–(63) in (69), we finally find,
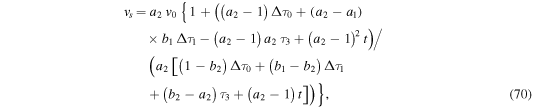
with t given by Equation (64) in terms of 
This phase ends when,  and the merged region enters in a deceleration phase. This deceleration phase is also described by Equations (51)–(53), where now the free parameter is
and the merged region enters in a deceleration phase. This deceleration phase is also described by Equations (51)–(53), where now the free parameter is 
3. VALIDATION OF THE MODEL
Even though the number of ICME interaction events is large, at least during the high activity phase of the cycle, when the mean rate of CMEs per day is ∼6 (Gopalswamy et al. 2005), there are a few reported cases of these events. We have found four ICME interaction events that have been extensively studied and reported in the literature and are suitable to validate our model.
The input CMEs parameters of our model has been reported in the literature, except for the duration of the eruption ( in our model). To estimate the CME duration time, we assume that this time is the FWHM of the brightness distribution as function of time, measured at 10 solar radii (Lara et al. 2004).
in our model). To estimate the CME duration time, we assume that this time is the FWHM of the brightness distribution as function of time, measured at 10 solar radii (Lara et al. 2004).
In addition, our model requires the mass-loss rate of the ASW. Following Wood et al. (2002) and Cranmer (2004), we assume that 
 yr−1. The in situ velocity and arrival time are obtained from the WIND spacecraft (Lepping et al. 1995; Ogilvie et al. 1995). Finally, we define the initial distance of the model as the position in which most of the CME properties used in this work are computed (∼10 solar radii = 0.046 AU).
yr−1. The in situ velocity and arrival time are obtained from the WIND spacecraft (Lepping et al. 1995; Ogilvie et al. 1995). Finally, we define the initial distance of the model as the position in which most of the CME properties used in this work are computed (∼10 solar radii = 0.046 AU).
3.1. Event of 2010 May 23
CME1 was observed by LASCO on board the SOHO spacecraft (e.g., Brueckner et al. 1995) on 2010 May 23 21:30 UT, with an initial velocity  km s−1 and a computed mass of
km s−1 and a computed mass of  g. The computed CME duration time is
g. The computed CME duration time is  Thus, the mass-loss rate is
Thus, the mass-loss rate is 
 yr−1 within a solid angle of
yr−1 within a solid angle of  (where
(where ![${{\rm{\Omega }}}_{1}=2\pi [1-\mathrm{cos}({w}_{1}/2)]$](https://content.cld.iop.org/journals/0004-637X/811/1/69/revision1/apj519156ieqn104.gif) being w1 the CME1 width).
being w1 the CME1 width).
The CME2 was observed by LASCO on 2010 May 24 18:04 UT, therefore the time interval between the CMEs is  The initial velocity and computed mass are
The initial velocity and computed mass are  km s−1 (leading edge) and
km s−1 (leading edge) and  g, respectively. The computed duration of this CME2 is
g, respectively. The computed duration of this CME2 is  and
and 
 yr−1 within a solid angle of
yr−1 within a solid angle of 
In Table 1, we present a summary of the parameters reported for this event; the constant factors obtained, by using the parameters in Table 1, are presented in Table 2; and Table 3 shows the comparison of the results of our model and the observations.
Table 1. Reported Parameters Used in Our Models
| Parameter | 2007 Jan 24 | 2010 May 23 | 2010 Aug 01 | 2012 Nov 09 |
|---|---|---|---|---|
 (hr) (hr) |
14.5 | 17.15 | 3.73 | 10.50 |
 (hr) (hr) |
2.0 | 2.85 | 1.1 | 1.55 |
 (hr) (hr) |
1.8 | 3.71 | 1.0 | 2.5 |
| m1 (gr) | 4.3 × 1015 | 1.5 × 1016 | 8.0 × 1015 | 4.66 × 1015 |
| m2 (gr) | 1.6 × 1016 | 1.0 × 1016 | 3.0 × 1016 | 2.27 × 1015 |
 ( ( yr−1) yr−1) |
7.21 × 10−14 | 3.46 × 10−13 | 2.74 × 10−13 | 9.04 × 10−14 |
 ( ( yr−1) yr−1) |
2.67 × 10−13 | 1.32 × 10−13 | 7.39 × 10−13 | 4.42 × 10−14 |
w1 ( ) ) |
85.0 | 60.0 | 80.0 | 90.0 |
w2 ( ) ) |
90.0 | 70.0 | 100.0 | 70.0 |
| v0 (km s−1) | 310 | 320 | 410 | 300 |
| v1 (km s−1) | 600 | 400 | 732 | 500 |
| v2 (km s−1) | 1350 | 650 | 1138 | 1100 |
Download table as: ASCIITypeset image
Table 2. Jump Factors of Our Models Indicated in Table 1
| Parameter | 2007 Jan 24 | 2010 May 23 | 2010 Aug 01 | 2012 Nov 09 |
|---|---|---|---|---|
| a1 | 1.94 | 1.25 | 1.78 | 1.66 |
| a2 | 4.35 | 2.03 | 2.77 | 3.66 |
| b1 | 3.61 | 17.3 | 13.69 | 4.52 |
| b2 | 13.35 | 6.56 | 36.98 | 2.21 |
| c1 | 1.86 | 13.84 | 7.66 | 2.71 |
| c2 | 3.07 | 3.23 | 13.32 | 0.60 |
Download table as: ASCIITypeset image
Table 3. Comparison of the Predicted and Observed Values of the ICMEs Interaction Events Indicated in Table 1
| MODEL RESULTS | ||||
|---|---|---|---|---|
| Parameter | 2007 Jan 24 | 2010 May 23 | 2010 Aug 01 | 2012 Nov 09 |
 (AU) (AU) |
0.33 | 0.69 | 0.20 | 0.35 |
 (hr) (hr) |
30.8 | 75.3 | 13.1 | 36.4 |
 (hr) (hr) |
71.0 | 100.2 | 52.3 | 95.8 |
 (km s−1) (km s−1) |
573 | 427 | 726 | 397 |
| OBSERVED DATA | ||||
| Parameter | 2007 Jan 24 | 2010 May 23 | 2010 Aug 01 | 2012 Nov 09 |
 (AU) (AU) |
0.45 | 0.52–0.77 | 0.16 | 0.16–0.46 |
 (hr) (hr) |
30.48 | NA | 12.91 | 19–36 |
 (hr) (hr) |
103.6 | 102.1 | 60.3 | 93.2 |
 (km s (km s  ) ) |
716 | 380 | 600 | 350 |
Download table as: ASCIITypeset image
The ICME interaction occurred at a distance in the range between 0.55 and 0.8 AU, and the resultant merged region reached the Earth on 2010 May 28 02:00 UT (Lugaz et al. 2012).
We set  km s−1, this is the ASW velocity measured in situ by WIND spacecraft on 2010 May 28 01:00 UT, before the arriving of the merged region.
km s−1, this is the ASW velocity measured in situ by WIND spacecraft on 2010 May 28 01:00 UT, before the arriving of the merged region.
The interaction occurred when WS1 was in its deceleration phase and WS2 had already reached its last phase of constant velocity. Figure 3 shows the velocities of  (panel (a)) and
(panel (a)) and  (panel (b)) as a function of distance without interaction. The dotted vertical line marks the collision distance.
(panel (b)) as a function of distance without interaction. The dotted vertical line marks the collision distance.
Figure 3. Velocities as a function of the distance of the working surfaces related to (a)  (
( ) and (b)
) and (b)  (
( ) for the event of 2010 May 23. The model predicts an interaction distance of 0.69 AU and an interaction time of 75.3 hr after the first eruption. The predicted arrival time at 1 AU of the merged region is 100.2 hr. The merged structure travels with an intermediate velocity (thick line) between the velocities of the
) for the event of 2010 May 23. The model predicts an interaction distance of 0.69 AU and an interaction time of 75.3 hr after the first eruption. The predicted arrival time at 1 AU of the merged region is 100.2 hr. The merged structure travels with an intermediate velocity (thick line) between the velocities of the  and
and  (discontinued lines). (d) Elongation as a function of time for the two ICMEs assuming that the ICMEs are moving at
(discontinued lines). (d) Elongation as a function of time for the two ICMEs assuming that the ICMEs are moving at  with respect of the observer—Sun line.
with respect of the observer—Sun line.
Download figure:
Standard image High-resolution imageBy using the Equations (17) and (18) in (29), we predicted that the arrival velocity is ∼427 km s−1, and the in situ arrival velocity was 380 km s−1. Therefore, the difference is 47 km s−1. In terms of time, we obtained a difference shorter than two hours between the predicted and the in situ arrival time. The interaction occurred at a distance of 0.69 AU and a time of 75.3 hr after the CME1 launch time.
Figure 3 panel (c) shows the trajectories (distance as function of time) of WS1 and WS2. The dashed lines represent these trajectories if they did not collide. The trajectory of the merged region is shown as the black thick line. The collision time is marked with the dotted vertical line.
In general, J-maps are used to analyze the collision between CMEs; for comparison with other works we included the elongation (the apparent angular distance computed assuming a fix angle of 90° between the Sun-observer and Sun-ICME direction lines) as function of time in panel (d)).
3.2. Events of 2007 January 24, 2010 August 01 and 2012 November 09
The event of 2007 January 24 was studied by Lugaz et al. (2008, 2009). CME1 was observed by LASCO on 2007 January 24 at 16:40:00 UT and CME2 on 2007 January 25 09:10:00 UT. The event of 2010 August 01 was reported by Temmer et al. (2012). The two eruptions were imaged by LASCO at 04:46:00 UT and 09:35:00 UT on on 2010 August 01, respectively. For the event of 2012 November 09, the most important parameters are reported by Mishra et al. (2014), CME1 was observed by STEREO A on 2012 November 09 at 20:22:00 UT and the CME2 on 2012 November 10 at 08:25:00 UT. We refer to these authors for the detailed analysis of each of these interaction events.
As for the event of 2010 May 23, we present in Table 1, a summary of the parameters reported for each event. The change factors (a, b, and c) are presented in Table 2. Table 3 shows the comparison of the results of our model and the observations.
Figure 4. Same as Figure 3 for the event of 2007 January 24. The interaction occurred at a distance of 0.33 AU and at a time of 30.8 hr after the first eruption. The predicted arrival time at 1 AU of the merged region is 71.0 hr.
Download figure:
Standard image High-resolution imageFigure 5. Same as Figure 3 for the event of 2010 August 01. The interaction occurred at a distance of 0.20 AU and at a time of 13.1 hr after the first eruption. The predicted arrival time at 1 AU of the merged region is 52.3 hr.
Download figure:
Standard image High-resolution imageThe events of 2010 May 23 and 2012 November 09 are very well reproduced by our model with differences less than 2 hr (interaction and arrival at 1 AU times) and in velocity less than 50 km s−1. In Figures 3 and 6, respectively, the velocities as functions of distance of WS1 (panel (a)) and WS2 (panel (b)) are shown. Both WSs are decelerated due to the fact that the material of the ICMEs are incorporated before the material of the ASW does it. In panel (c), we present the trajectories of the WSs. The collision time is marked as a dotted vertical line. After this time the thick black line shows the trajectory of the merged region that reaches 1 AU. Dashed lines show the trajectories of both WSs if the interaction would not have taken place.
Figure 6. Same as Figure 3 for the event of 2012 November 09. The model predict an interaction distance of 0.35 AU and at a time of 36.4 hr after the first eruption. The predicted arrival time at 1 AU of the merged region is 95.8 hr.
Download figure:
Standard image High-resolution imageIt is interesting to note that our results for the event of 2010 May 23 do not support the argument of deflection of Lugaz et al. (2012), who found a large deflection of ICME2 in such way that it never reaches the Earth.
For the event of 2010 August 01, the WS2 is in phase B2 at the moment of the interaction (Figure 5). The WS2 accelerates due to the fact that all of the available ASW material was incorporated to the WS2 before the ICME2 material had been engulfed. The difference between the computed and observed interaction times is of a few minutes, while the predicted arrival time differs from the observed value by less than eight hours. This difference may be caused by another CME, which was launched before CME1 (Liu et al. 2012). This third CME probably interacted with the merged structure (of WS1 and WS2) before 1 AU. This interaction may have formed a new merged region which was decelerated in the process, reaching 1 AU in a longer time and with a slower velocity.
The event of 2007 January 24 was in phase C2 at the moment of interaction (Figure 4). This event has the major differences with the observations due to two factors: (i) the uncertainty on the mass computations: Jackson et al. (2009) reported masses of 2.1 × 1016 g and 2.0 × 1016 g for the CMEs whereas Lugaz et al. (2009) reported masses of 4.3 × 1015 g and 1.6 × 1016 g, and (ii) the presence of a CIR in the interplanetary medium during its evolution.
The in situ observations show a CIR around the time when the merged region arrival was predicted and in the simulations of this event Lugaz et al. (2008) and Odstrcil & Pizzo (2009) found that this CIR interacted with the ICMEs. In this case, the model predicted the dynamics of the merged region without the interaction with the CIR. At the present stage, our model is not able to include ICME–CIR interactions. In any case, we have included this event to show that the model gives erroneous outputs when the initial conditions are not set correctly.
4. CONCLUSIONS
We have developed an analytical model to describe the dynamics of the interaction of two consecutive coronal mass ejections in the interplanetary medium. Our model is able to predict the distance and time of the interaction as well as the velocity of the resulting merged region. Moreover, the model estimates the arrival time and velocity of this region as a function of heliospheric distance, making it a useful tool for space weather research.
To validate it, we have applied our model to a set of well observed interaction events of 2007 January 24, 2010 May 23, 2010 August 01 and 2012 November 09. For the events of 2010 May 23 and 2012 November 09, the time difference between our results and the observations are lower than 2 hr (for both times: the interaction and the arrival at 1 AU); and the differences in velocity are lower than 50 km s−1.
The event of 2010 August 01 was a more complex event, and therefore, we predict the arrival time of the merged region at 1 AU with less than 8 hr of difference, however, the computed collision time is in a very good agreement with the observed value.
The predicted collision time of the event of 2007 January 24 matches the observed value. Nevertheless, the large difference between the observed and arrival times is probably due to the fact that during this event in particular more than two ICMEs and/or CIRs interacted in the interplanetary space.
Finally, the initial parameters of the model are observables, and it is relatively simple to implement, we conclude that it is well situated to use it in terms of space weather predictions.
This work was partially supported by CONACyT grants 344896, 165584, 101356/09, 113605, and 179588; and UNAM/PAPIIT grants INI106212, IG100214, IN112412-3, and IN112014.








