ABSTRACT
We explore the connections between the evolving galaxy and active galactic nucleus (AGN) populations. We present a simple phenomenological model that links the evolving galaxy mass function and the evolving quasar luminosity function, which makes specific and testable predictions for the distribution of host galaxy masses for AGNs of different luminosities. We show that the ϕ∗ normalizations of the galaxy mass function and of the AGN luminosity function closely track each other over a wide range of redshifts, implying a constant "duty cycle" of AGN activity. The strong redshift evolution in the AGN L∗ can be produced by either an evolution in the distribution of Eddington ratios, or in the mbh/m∗ mass ratio, or both. To try to break this degeneracy we look at the distribution of AGNs in the Sloan Digital Sky Survey (mbh, L) plane, showing that an evolving ratio 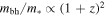 reproduces the observed data and also reproduces the local relations that connect the black hole population with the host galaxies for both quenched and star-forming populations. We stress that observational studies that compare the masses of black holes in active galaxies at high redshift with those in quiescent galaxies locally will always see much weaker evolution. Evolution of this form would produce, or could be produced by, a redshift-independent mbh–σ relation and could explain why the local mbh–σ relation is tighter than mbh–m* even if σ is not directly linked to black hole growth. Irrespective of the evolution of mbh/m*, the model reproduces both the appearance of "downsizing" and the so-called "sub-Eddington boundary" without any mass-dependence in the evolution of black hole growth rates.
reproduces the observed data and also reproduces the local relations that connect the black hole population with the host galaxies for both quenched and star-forming populations. We stress that observational studies that compare the masses of black holes in active galaxies at high redshift with those in quiescent galaxies locally will always see much weaker evolution. Evolution of this form would produce, or could be produced by, a redshift-independent mbh–σ relation and could explain why the local mbh–σ relation is tighter than mbh–m* even if σ is not directly linked to black hole growth. Irrespective of the evolution of mbh/m*, the model reproduces both the appearance of "downsizing" and the so-called "sub-Eddington boundary" without any mass-dependence in the evolution of black hole growth rates.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Over the last few years there has been a lot of interest in the cosmic "co-evolution" of supermassive black holes (SMBHs) and the stellar populations of the galaxies that they reside in. This has been motivated on the one hand by the tight scaling relations that have been established between the masses of the black holes and various parameters of the host galaxies (e.g., Kormendy & Richstone 1995; Magorrian et al. 1998; Ferrarese & Merritt 2000; Gebhardt et al. 2000; Tremaine et al. 2002; Marconi & Hunt 2003; Häring & Rix 2004; Ferrarese & Ford 2005; Greene & Ho 2006, 2007; Aller & Richstone 2007; Greene et al. 2008; Graham et al. 2011; Sani et al. 2011; Vika et al. 2012; McConnell & Ma 2013), and on the other by the overall similarities between the evolution of the star formation rate (SFR) density of the universe and the luminosity density that is ascribed to SMBH accretion (e.g., Boyle & Terlevich 1998; Franceschini et al. 1999; Heckman et al. 2004; Marconi et al. 2004; Hasinger et al. 2005; Silverman et al. 2009; Zheng et al. 2009). This paper seeks to link directly the evolution of the galaxy and active galactic nucleus (AGN) populations via a simple phenomenological model.
Looking first at galaxies, almost all galaxies can be broadly classified into a few distinct populations. The majority of star-forming (SF) galaxies have an SFR that is strongly correlated to their existing stellar mass, producing the so-called "Main Sequence" in which the specific SFR (or sSFR) varies only weakly with stellar mass. This characteristic sSFR of the Main Sequence, however, increases strongly with look-back time (Daddi et al. 2007; Elbaz et al. 2007; Pannella et al. 2009; Speagle et al. 2014) and is about a factor of 20 higher at z ∼ 2 compared to the present day value. A small percentage of SF galaxies have significantly elevated sSFR, above the Main Sequence. It appears that the fraction of these "outliers" is more or less constant to z ∼ 2 (Sargent et al. 2012) and that they represent of the order of 10% of the integrated star formation that is occurring at any epoch. There is also a large population of "quenched" galaxies in which the star formation is substantially lower than on the Main Sequence, producing an sSFR that is much lower than the inverse Hubble time. Our understanding of the physical processes that lead to the quenching of SF galaxies is still quite limited and a number of plausible physical mechanisms have been proposed (some of which involve AGNs directly). However, the main empirical, or phenomenological, features of this quenching process are quite well understood based on the characteristic of the evolving population(s) of galaxies.
As the available data on the galaxy population at substantial look-back times has improved, new analysis techniques have been introduced that take a purely empirical (phenomenological) approach to the data, see, e.g., Peng et al. (2010) and Behroozi et al. (2013a). These are complementary to the semi-analytic models of galaxy evolution (e.g., Somerville et al. 2008; Conroy & Wechsler 2009; Henriques et al. 2014).
The approach in Peng et al. (2010) was to identify a few striking simplicities exhibited by the galaxy population(s) and to explore the consequences of these, where possible analytically, in terms of the most basic continuity equations linking the galaxy population(s) at different epochs. The Peng et al. (2010) analysis was based on dividing the galaxy population into two components, the SF Main Sequence (including the outliers) and the quenched population of passive galaxies. Much of the Peng et al. (2010) formalism is based on the observation that the characteristic Schechter M∗ of the mass-function ϕ(m) of the SF population has been more for less constant back to at least z ∼ 2.5 (and likely to z ∼ 4) despite the substantial increase in stellar mass (by a factor of 10–30) of any galaxy that stays on the SF Main Sequence over this same time period (Bell et al. 2003, 2007; Ilbert et al. 2010, 2013; Pozzetti et al. 2010). The Peng et al. (2010) continuity formalism is very successful at reproducing the single and double Schechter (Press & Schechter 1974) shapes of the mass functions of SF and passive galaxies in the Sloan Digital Sky Survey (SDSS) and also explains the quantitative relations between the Schechter parameters of these mass functions that constitute a test of the approach. The formalism allows easy computation of things like the quenching rate of galaxies, the mass function of galaxies that are undergoing quenching at any epoch, and so on. The alternative phenomenological approach of "abundance matching" (Behroozi et al. 2013a) provides similar results, in terms of mass functions and star formation histories. With these recent developments, we now have a self-consistent, empirical ("phenomenological") description of the evolving galaxy population at least back to z ∼ 4 in terms of the evolving mass-functions of both the SF and quenched populations of galaxies.
Turning to the AGN, the most basic description of the evolving population is the bolometric luminosity function (i.e., quasar luminosity function, QLF), i.e., ϕ(L, z). Large homogeneous samples of AGNs have been created, from optical surveys such as SDSS (Schneider et al. 2010; Ross et al. 2013) and deep X-ray surveys, out to redshifts z ∼ 5 (e.g., Hasinger et al. 2005; Brown et al. 2006; Silverman et al. 2008; Brusa et al. 2010; Civano et al. 2011; Kalfountzou et al. 2014; Ueda et al. 2014). These QLF studies have found that the QLF ϕ(L) is best described by a double power law, i.e., two power-law segments broken at a characteristic luminosity L∗,

These studies tend to agree that the increase in the number density of luminous quasars with increasing redshift is mostly driven by an evolution of L∗ at redshifts below z ∼ 2. The exact shape of the QLF and need for evolution of other parameters is still debated (Ueda et al. 2003; Barger et al. 2005; Croom et al. 2009; Aird et al. 2010; Assef et al. 2011).
The double power-law shape of the QLF contrasts the galaxy mass function ϕ(m), which is clearly better described by one or more Schechter functions, i.e., a power law at low masses (or luminosities) and an exponential cutoff at masses above a characteristic mass M∗. This difference in the shapes of these two most basic descriptions of the two populations is interesting in that AGNs are being harbored in galaxies and one might naively expect similarities between these two functions. This difference will form an important part of the current analysis.
The luminosity of an individual AGN can be expressed as

where L is given in erg s−1, λ is the Eddington ratio and mbh is the mass of the central black hole in units of solar mass. The SMBH mass is therefore a key quantity in understanding both an individual AGN and the AGN population. Unfortunately, black hole masses can be measured reliably with dynamical modeling only for a small number of nearby sources in which the SMBH is generally quiescent (e.g., Gültekin et al. 2009; Schulze & Gebhardt 2011; Graham & Scott 2013; Kormendy & Ho 2013; McConnell & Ma 2013; Rusli et al. 2013, and references within). Objects that are actively accreting and/or that are further away need to be analyzed with different techniques. For AGNs that show broad lines in their spectra it is possible to determine mbh by conducting reverberation mapping campaigns (see the review by Peterson 2013, and references within). The results of such campaigns make it possible to construct "single-epoch" mass estimators, which allow the determination of mbh of AGNs based on luminosity and linewidth. Systematic uncertainties in these estimators are calibrated using a sample of local AGNs for which black hole masses are statistically known from the mbh–σ of local (inactive) galaxies.
Early suggestions that the distribution of specific accretion rates onto black holes has no dependence on black hole or galaxy mass (Yu et al. 2005; Kollmeier et al. 2006; Merloni & Heinz 2008), have gained further observational support from analysis of the PRIMUS and COSMOS survey fields (Aird et al. 2012; Bongiorno et al. 2012). We will adopt a similar assumption in this paper.
Observations in the local universe have revealed several interesting correlations between the mass of the SMBH in the center of a given galaxy and various quantities describing the surrounding galaxy. Specifically, quite tight relations have been established with the stellar velocity dispersion ( ) and with the stellar mass of the bulge in the galaxy (mbh–mbulge; Magorrian et al. 1998; Ferrarese & Merritt 2000; Gebhardt et al. 2000; Marconi & Hunt 2003). Canonical values of the ratio between mbh and mbulge are between 10−3 and 10−2.7 (Häring & Rix 2004). The recent extensive review by Kormendy & Ho (2013) has argued for larger values, up to 10−2.3, mainly due to differentiation between bulges and pseudo-bulges, by omitting mergers in progress and by the inclusion of dark matter in dynamical modeling. Other scaling relations have been proposed, such as mbh − n, where n is the Sérsic index describing the light profile of the galaxy, mbh–mhalo where mhalo is the mass of the dark matter halo, and mbh–m* where m* is the integrated stellar mass of the galaxy (Sani et al. 2011). All these relations tend to show more scatter, but the basic difficulty is that most of these galaxy parameters are strongly correlated with each other. It has been claimed that the correlation between mbh–m* is more fundamental than the mbh–mbulge relation (Marleau et al. 2013), especially in SF hosts, which could then help explain the AGN sources in bulgeless, pure disk galaxies that have been observed (Simmons et al. 2013). In this paper we will base the analysis on mbh–m* simply because the available mass functions of galaxies generally utilize the integrated stellar mass rather than the bulge mass, especially at high redshift.
) and with the stellar mass of the bulge in the galaxy (mbh–mbulge; Magorrian et al. 1998; Ferrarese & Merritt 2000; Gebhardt et al. 2000; Marconi & Hunt 2003). Canonical values of the ratio between mbh and mbulge are between 10−3 and 10−2.7 (Häring & Rix 2004). The recent extensive review by Kormendy & Ho (2013) has argued for larger values, up to 10−2.3, mainly due to differentiation between bulges and pseudo-bulges, by omitting mergers in progress and by the inclusion of dark matter in dynamical modeling. Other scaling relations have been proposed, such as mbh − n, where n is the Sérsic index describing the light profile of the galaxy, mbh–mhalo where mhalo is the mass of the dark matter halo, and mbh–m* where m* is the integrated stellar mass of the galaxy (Sani et al. 2011). All these relations tend to show more scatter, but the basic difficulty is that most of these galaxy parameters are strongly correlated with each other. It has been claimed that the correlation between mbh–m* is more fundamental than the mbh–mbulge relation (Marleau et al. 2013), especially in SF hosts, which could then help explain the AGN sources in bulgeless, pure disk galaxies that have been observed (Simmons et al. 2013). In this paper we will base the analysis on mbh–m* simply because the available mass functions of galaxies generally utilize the integrated stellar mass rather than the bulge mass, especially at high redshift.
In fact, almost all of the properties of galaxies that host AGNs are still widely debated. Although there are undoubtedly some active AGNs found in quenched galaxies, the bulk of radiatively efficient AGNs seem to reside in SF galaxies (Netzer 2009; Silverman et al. 2009; Schawinski et al. 2010; Koss et al. 2011; Cimatti et al. 2013; Rosario et al. 2013; Matsuoka et al. 2014), especially in those relatively low-luminosity systems where the host galaxy can be most easily discerned. Nevertheless, it is still not entirely clear what fraction of AGNs is situated in quenched galaxies and whether this fraction changes with AGN luminosity.
Many studies have suggested that there is some redshift evolution in mass scaling relations (Peng et al. 2006; Decarli et al. 2010; Merloni et al. 2010; Trakhtenbrot & Netzer 2010; Bennert et al. 2011; Sijacki et al. 2014), but others have found no significant evolution (Jahnke et al. 2009; Cisternas et al. 2011; Mullaney et al. 2012; Schramm & Silverman 2013) or have argued that an observed evolution can be fully explained with selection effects (Schulze & Gebhardt 2011; Schulze & Wisotzki 2014). The redshift evolution of the scaling relations is still debated and we will explore different possibilities in the current paper within our model framework. We will also emphasize the methodological issues associated with the choice of samples.
Several studies have also attempted to constrain different aspects of black hole evolution with empirical or semi-empirical approaches that model the evolving black hole mass function, accretion rate, QLF, duty cycle, accretion efficiency, or some subset of these quantities (Merloni 2004; Shankar et al. 2004, 2009, 2013b; Yu & Lu 2004; Merloni & Heinz 2008; Hopkins & Hernquist 2009; Shen 2009; Cao 2010; Li et al. 2011; Steinhardt et al. 2011; Conroy & White 2013; Novak 2013; Goulding et al. 2014).
In this work, we aim to apply a similar phenomenological approach that has proved so successful in describing the evolving galaxy population evolution to the evolving AGN population. We will take the simplest observables of the population and try to infer the underlying simplicities of the situation and use straightforward prescriptions to construct a simple model that can both explain the salient observational data and which can be used to make simple testable predictions for other quantities. A focus of this work is to try to use our improved understanding of the evolving galaxy population, and especially of the evolving mass function ϕ(m*) of galaxies to high redshifts, to interpret the evolution of the AGN population. We aim thereby to create a simple global model to interpret the evolving AGN population and to enable us to evaluate biases that may arise in observational work, e.g., through the use of luminosity-selected samples. The model is based on the construction of the AGN QLF via a double convolution of the underlying host galaxy mass function with a scatter function representing the black hole to stellar mass ratio, and with an Eddington ratio distribution.
Hopkins et al. (2008b) and Hopkins & Quataert (2010) have also used the observed galaxy mass functions as a basis for modeling the AGN population using AGN lightcurves obtained from simulations. A more similar approach to ours has been used by Aird et al. (2013) with an observationally driven model that connects AGN and galaxy evolution out to z ∼ 1, based on observational data from the PRIMUS survey (Aird et al. 2012). They have shown that it is possible to reproduce the luminosity function measurements with a mass-independent distribution of specific accretion rates, i.e., linking the AGN QLF to the galaxy mass function. Hickox et al. (2014) has also used a simple phenomenological approach and shown that the main observational trends (such as QLF and SFR-LAGN correlations) can be recovered by assuming that all SF galaxies host an AGN and that star formation and black hole accretion are correlated on ∼ 100 Myr timescales, i.e., in this case they were linking the growth of the black holes and stellar populations. A very recent paper of Veale et al. (2014) has, like the current work, explored the links between the evolving galaxy (and halo) mass functions and the observed AGN QLF via a convolution approach. Veale et al. (2014) have emphasized the degeneracies between the "mass function" and "mass growth" approaches when only the AGN QLF is considered. In the current work, we incorporate other observational data, most notably the distribution of AGNs in the (mbh, L) plane, to move beyond the information in the QLF alone.
The layout of the paper is as follows. In Section 2 we first state the three simple Ansätze that are used to construct the model. We then show in Section 3 how the quasar ϕ(L) can be simply constructed from the galaxy  and Eddington ratio distribution
and Eddington ratio distribution  via a convolution and how the parameters of these distribution functions are connected, and make testable predictions of the mass distribution of the host galaxies of quasars selected at different luminosities. In Section 4 we review the observed epoch-dependent
via a convolution and how the parameters of these distribution functions are connected, and make testable predictions of the mass distribution of the host galaxies of quasars selected at different luminosities. In Section 4 we review the observed epoch-dependent  and ϕ(L,z) functions and then in Section 5 we compare these within the framework of the convolution model to derive interesting conclusions about the duty cycle of AGNs.
and ϕ(L,z) functions and then in Section 5 we compare these within the framework of the convolution model to derive interesting conclusions about the duty cycle of AGNs.
Up until this point, the model is completely general. In Section 6, we then consider different possibilities for the evolution of the  ratio and show that one particular choice can explain the observed distribution of luminous quasars in the (mbh, L) plane and local scaling relations of black holes in both SF and passive galaxies and the possible differences in evolution of active and passive systems. Section 7 presents a discussion of some further implications of both the general model and the specific
ratio and show that one particular choice can explain the observed distribution of luminous quasars in the (mbh, L) plane and local scaling relations of black holes in both SF and passive galaxies and the possible differences in evolution of active and passive systems. Section 7 presents a discussion of some further implications of both the general model and the specific  implementation, differences between
implementation, differences between  and mbh–σ, the appearance of downsizing within the AGN population, and the pervasive biases that enter into luminosity-selected samples. The paper then concludes with a summary section.
and mbh–σ, the appearance of downsizing within the AGN population, and the pervasive biases that enter into luminosity-selected samples. The paper then concludes with a summary section.
Throughout the paper, we will assume a ΛCDM cosmology, with the parameters  = 0.3,
= 0.3,  = 0.7, and H0 = 70 km s−1 Mpc−1. Luminosities will be given in units of erg s−1 and will refer to bolometric luminosities, unless specified otherwise. We use the term "dex" to denote the antilogarithm, i.e., n dex = 10n. We also define all distribution functions, i.e., the SF galaxy mass function
= 0.7, and H0 = 70 km s−1 Mpc−1. Luminosities will be given in units of erg s−1 and will refer to bolometric luminosities, unless specified otherwise. We use the term "dex" to denote the antilogarithm, i.e., n dex = 10n. We also define all distribution functions, i.e., the SF galaxy mass function  the associated SF galaxy black hole mass function
the associated SF galaxy black hole mass function  the AGN luminosity function ϕ(L), and the probability distribution of Eddington ratio ξ(λ), in log space. This leads to power-law exponents that differ by unity relative to distribution functions defined in linear space. Therefore, the units of
the AGN luminosity function ϕ(L), and the probability distribution of Eddington ratio ξ(λ), in log space. This leads to power-law exponents that differ by unity relative to distribution functions defined in linear space. Therefore, the units of 
 , and
, and  are Mpc−3 dex−1.
are Mpc−3 dex−1.
2. ANSÄTZE
The essence of this phenomenological approach is to make a limited number of simple Ansätze that allow us to construct a model using analytic techniques, or very elementary numerical modeling, based on straightforward representations of the most important features of the observational data. These Ansätze are in a sense "assumptions" and a decisive observational disproof of any of them would largely invalidate the model. Clearly they are very unlikely to be exactly true. Their value, as the basis for a simple "toy model," is that we believe they are likely to be broadly true.
The three Ansätze in the current work are as follows:
- 1.radiatively efficient AGNs are found in SF galaxies,
- 2.the probability distribution of the Eddington ratio does not depend on the black hole mass of the system, and
- 3.the mass of the central black hole is linked to the stellar mass (
 ), with some scatter, and we will for simplicity set
), with some scatter, and we will for simplicity set 
The justification for the first and the third of these has been reviewed in the Introduction and the second is closely related to the assumption of Aird et al. (2013). We will justify these, and the choice of β ∼ 1, further below. Of course, there are a number of other implicit assumptions that are being made: the observational data are not wildly wrong, individual black hole and stellar mass measurements are not systematically biased, the cosmological model is more or less correct, and so on. We will not consider these further.
3. THE ORIGIN OF THE QLF
With our Ansätze, we can use our knowledge of the mass function of galaxies to construct the black hole mass function. To do this, we start with the mass function of SF galaxies and then impose a black hole to stellar mass ratio  with an additional log-normal scatter of η, to create a black hole mass function in SF hosts. This will serve as the basis for the radiatively efficient AGN population. In the first part of the paper, we will set the scatter η = 0 for initial analytic simplicity, before reintroducing it with η ∼ 0.5 when we evaluate the model numerically.
with an additional log-normal scatter of η, to create a black hole mass function in SF hosts. This will serve as the basis for the radiatively efficient AGN population. In the first part of the paper, we will set the scatter η = 0 for initial analytic simplicity, before reintroducing it with η ∼ 0.5 when we evaluate the model numerically.
If radiatively efficient accretion onto central black holes is only occurring in SF hosts, the QLF can be created from a convolution of the black hole mass function in SF galaxies ϕBH(mbh,z) with a probability distribution of the Eddington ratio λ,

where ϕ(L, z) is the resulting QLF, and ξ (λ, z) is the probability distribution of the Eddington ratio, λ, as defined in Equation (2).
3.1. Convolution of Schechter Functions with Power-law Eddington Ratios
As noted above in Equation (3), the QLF will, with our Ansätze, be a convolution of the black hole mass function ϕBH(mbh) (itself derived from the stellar mass function of SF galaxies  ) and the distribution of Eddington ratios
) and the distribution of Eddington ratios  which gives the distribution of luminosities for black holes of a given mass. In this section we look at the general features of the ξ(λ) distribution that are needed to produce a double power-law QLF from a Schechter-like mass function and derive the connections that will exist between the parameters of these different functions.
which gives the distribution of luminosities for black holes of a given mass. In this section we look at the general features of the ξ(λ) distribution that are needed to produce a double power-law QLF from a Schechter-like mass function and derive the connections that will exist between the parameters of these different functions.
First, we immediately note that in a model with a mass-independent ξ(λ) and an input Schechter mass function, the only way to produce a power law at the bright end of the QLF (with slope γ2) is to have a ξ(λ) that is also a power law of the same slope at high values of the Eddington ratio. This power-law will then ensure that there is a high-end power law in the QLF even as the mass function drops off exponentially. This is shown in Appendix

with γ2, the bright end slope of the QLF.
At the faint end, we may also expect a power-law QLF but now the QLF faint end slope γ1 will be given by the steeper of the low end slope of ϕBH(mbh) and the low end slope of ξ(λ), which we denote by δ1 (see also the discussion in Veale et al. 2014). Figure 1 illustrates what is happening with the faint end of the QLF (with slope) for different Eddington ratio assumptions.
Figure 1. Schematic representation of our procedure to create the QLF. Starting from the star-forming mass function (leftmost) we use an  scaling to get the mass function of SMBH in star-forming galaxies, with scatter as required (second panel). We convolve it with the Eddington ratio distribution (in the third panel) to create the QLF in the rightmost panel. Blue and red Eddington ratio distributions differ in the choice of parametrization of the low end slope. The faint end slope of the QLF will be the same as the low mass slope of the galaxy mass function or the low end slope of the Eddington ratio distribution, depending on the relative steepness of these two slopes. A short summary of the connections between parameters of the QLF and parameters of the contributing functions is given in Equation (12).
scaling to get the mass function of SMBH in star-forming galaxies, with scatter as required (second panel). We convolve it with the Eddington ratio distribution (in the third panel) to create the QLF in the rightmost panel. Blue and red Eddington ratio distributions differ in the choice of parametrization of the low end slope. The faint end slope of the QLF will be the same as the low mass slope of the galaxy mass function or the low end slope of the Eddington ratio distribution, depending on the relative steepness of these two slopes. A short summary of the connections between parameters of the QLF and parameters of the contributing functions is given in Equation (12).
Download figure:
Standard image High-resolution imageWe can express this as

The natural conclusion of a mass-independent Eddington rate distribution is that the faint end of the QLF is set up by either the low end slope of the underlying black hole mass function or by the low end slope of the Eddington ratio function. If the logarithmic slope of the mbh versus m* relation is β as above, then the faint end slope of the black hole mass function will be related to that of the SF galaxies by 
We note at this point that there is good observational evidence that the faint end QLF slope, γ1, is similar to the observed low mass slope of the mass function of SF galaxies, αSF, allowing for the reversal of sign in our definition. The QLF faint end slope,  is usually observed to be between 0.3 and 0.9 (Hasinger et al. 2005; Hopkins et al. 2007; Aird et al. 2010; Masters et al. 2012; Ueda et al. 2014). On the other hand, the observed values of αSF range from −0.6 to −0.2 (Baldry et al. 2008; Pérez-González et al. 2008; Peng et al. 2010; González et al. 2011; Kajisawa et al. 2011; Baldry et al. 2012; Lee et al. 2012) with most newer studies converging around αSF ∼ −0.4.
is usually observed to be between 0.3 and 0.9 (Hasinger et al. 2005; Hopkins et al. 2007; Aird et al. 2010; Masters et al. 2012; Ueda et al. 2014). On the other hand, the observed values of αSF range from −0.6 to −0.2 (Baldry et al. 2008; Pérez-González et al. 2008; Peng et al. 2010; González et al. 2011; Kajisawa et al. 2011; Baldry et al. 2012; Lee et al. 2012) with most newer studies converging around αSF ∼ −0.4.
The data are therefore consistent with the idea that  This suggests that γ1 is indeed being set by the low end slope of the black hole mass function (and not the low end of the Eddington ration distribution) and further that β ∼ 1. We will henceforth assume that this is the case, i.e., that
This suggests that γ1 is indeed being set by the low end slope of the black hole mass function (and not the low end of the Eddington ration distribution) and further that β ∼ 1. We will henceforth assume that this is the case, i.e., that  This then means that the low end slope δ1 of ξ(λ) can take any value that is shallower than this, i.e.,
This then means that the low end slope δ1 of ξ(λ) can take any value that is shallower than this, i.e.,  The high- and low-end power laws of the Eddington ratio distribution will meet in a knee at a characteristic Eddington ratio, which we denote by
The high- and low-end power laws of the Eddington ratio distribution will meet in a knee at a characteristic Eddington ratio, which we denote by  , at which point the value of ξ(λ) has a characteristic value
, at which point the value of ξ(λ) has a characteristic value 
3.2. The Simplest Eddington Ratio Distribution that Reproduces the Shape of the QLF
To further demonstrate our approach we use the simplest function possible for the Eddington ratio distribution that reproduces, analytically, the required broken power-law shape of QLF. We use a "triangular" distribution in which some fraction, fd, of objects is active above a certain threshold value  with an Eddington ratio distribution that is a single power law with slope δ2, while (1 – fd) of the objects are completely inactive. Effectively this sets the low end slope
with an Eddington ratio distribution that is a single power law with slope δ2, while (1 – fd) of the objects are completely inactive. Effectively this sets the low end slope 
The exact functional form of  can then be written as
can then be written as

where  in constrained by the requirement that all of the objects have to be either active or inactive, so ξ in this case has to integrate to a duty cycle fd.
in constrained by the requirement that all of the objects have to be either active or inactive, so ξ in this case has to integrate to a duty cycle fd.
In Appendix  will be related to the parameters of the original distribution functions through a formula describing the population, which is analogous to Equation (2) of individual black holes, i.e.,
will be related to the parameters of the original distribution functions through a formula describing the population, which is analogous to Equation (2) of individual black holes, i.e.,

where the ΔL factor denotes a small multiplicative factor that is weakly dependent on γ2 and varying by less than 0.15 dex.
In the same  normalization of the QLF, i.e., the value of ϕL at L = L∗ will be linked to the normalization of the galaxy mass function
normalization of the QLF, i.e., the value of ϕL at L = L∗ will be linked to the normalization of the galaxy mass function  and the normalization of the Eddington ratio distribution,
and the normalization of the Eddington ratio distribution, 

where the Δϕ denotes once again a small multiplicative factor, weakly dependent on γ2 and varying by less than 0.15 dex. This is not surprising and is stating the fact that the normalization of objects at a given luminosity L∗ is connected with the normalization of the contributing functions at  and
and  Simply put, if there are more objects at mass M∗ and more of them are active at
Simply put, if there are more objects at mass M∗ and more of them are active at  then we expect also more objects with a corresponding luminosity
then we expect also more objects with a corresponding luminosity 
3.3. Broken Power-law Eddington Ratio Distribution and Generalized Duty Cycle
Even though the triangular distribution of ξ(λ) is a simple and analytically tractable one, it is unlikely to describe the real AGN population. In the remainder of this paper we will adopt a more realistic broken power-law distribution of the Eddington ratio given by

where we set δ1 = 0 for further analysis. This function fits both observations and hydrodynamical simulations better, which show no sudden cutoff in the Eddington ratio distribution at some single value (e.g., Novak et al. 2011; Kelly & Shen 2013). This distribution diverges logarithmically at the low λ end. Since the integral of ξ(λ) will therefore reach unity at some low value of  all black holes are "active" at some very low level and we need no longer consider "inactive" ones.
all black holes are "active" at some very low level and we need no longer consider "inactive" ones.
As discussed in Section 3.1, this distribution will also reproduce the same shape of the QLF as the "triangular" distribution just discussed, provided that 
We note that such a distribution, (with a sharp break at  instead of the "smooth" version above), would naturally arise if individual AGNs are boosted to some initial Eddington ratio above
instead of the "smooth" version above), would naturally arise if individual AGNs are boosted to some initial Eddington ratio above  (the distribution of which is given by γ2) and thereafter decay exponentially with a constant decay time τ. In this case, the concept of the "duty cycle" fd in the previous section is replaced by the value of
(the distribution of which is given by γ2) and thereafter decay exponentially with a constant decay time τ. In this case, the concept of the "duty cycle" fd in the previous section is replaced by the value of  If the "boost plus decay" scenario is relevant, then it is easy to see that, if AGNs are activated at some fractional rate η per SF galaxy per unit time (e.g., Hopkins et al. 2005), then
If the "boost plus decay" scenario is relevant, then it is easy to see that, if AGNs are activated at some fractional rate η per SF galaxy per unit time (e.g., Hopkins et al. 2005), then

so that  is the fraction of black holes that are activated in the time interval corresponding to their subsequent decay time. This is quite a useful definition of duty cycle.
is the fraction of black holes that are activated in the time interval corresponding to their subsequent decay time. This is quite a useful definition of duty cycle.
Of course, other scenarios could also produce this ξ(λ) distribution and a more general "duty cycle" could be defined as the fraction of black holes accreting above  (as in the triangular distribution above). In this particular case, as shown in Appendix
(as in the triangular distribution above). In this particular case, as shown in Appendix

The point is that the value of  is a good indicator of a generalized duty cycle.
is a good indicator of a generalized duty cycle.
If  then the exact choice
then the exact choice  below
below  is of no great importance to the convolution model and the connections between the parameters, which we can derive analytically in the simplified model as in Equations (4), (5), (7), and (8) will still hold. Specifically, we can write
is of no great importance to the convolution model and the connections between the parameters, which we can derive analytically in the simplified model as in Equations (4), (5), (7), and (8) will still hold. Specifically, we can write

where we have now also explicitly shown a δ1 dependence in the Δ factors because this corrective factor will also depend on our exact choice of low slope of the Eddington ratio distribution. Now using the mbh/m* relation, we can also connect the observed L∗ of the QLF to the M∗ of the SF galaxy mass function with

3.4. Predictions of the Convolution Model
If the QLF is indeed produced by the convolution described in the previous two sections, then we can immediately see in general terms how the mass distribution of AGNs, or host galaxies of AGNs, selected at a given luminosity will vary with that selection luminosity. This is shown in Figure 2 where we show the mass functions of galaxies and black holes. The masses and number densities are normalized respectively by the M∗ and  of the input Schechter mass function of the SF galaxies. These distributions are plotted for different AGN luminosities relative to the knee luminosity L∗ in the QLFs (see also Equation (1)). To generate this plot we used the model for ξ(λ) considered in the previous section, i.e., with a flat ξ below
of the input Schechter mass function of the SF galaxies. These distributions are plotted for different AGN luminosities relative to the knee luminosity L∗ in the QLFs (see also Equation (1)). To generate this plot we used the model for ξ(λ) considered in the previous section, i.e., with a flat ξ below  and with 0.5 dex scatter in the black hole to stellar mass relation. With this normalization the figures apply at all redshifts. Several points should be noted on this figure.
and with 0.5 dex scatter in the black hole to stellar mass relation. With this normalization the figures apply at all redshifts. Several points should be noted on this figure.
First, all of the mass functions (of both black holes and host galaxies) always show a peak at some mass. This is quite unlike the input mass function of SF galaxies, and thus also of black holes, which increase monotonically to lower masses. The peak arises because the low-mass end of the input mass function is modulated by the high λ part of ξ(λ), simply because it is the highest Eddington ratios that pull the lowest mass black holes (and hosts) into a given luminosity bin. The low mass end of these mass distributions should therefore have a slope of  i.e., with
i.e., with  and
and  (see below) we predict a low mass slope of +1.6. This is a quite generic and robust prediction of the convolution model and is independent of the choice of δ1, the low λ behavior of ξ(λ) discussed above. This is because for most luminosities, the high-mass end of the mass functions in Figure 2 is dominated by the exponential fall-off of the input mass function.
(see below) we predict a low mass slope of +1.6. This is a quite generic and robust prediction of the convolution model and is independent of the choice of δ1, the low λ behavior of ξ(λ) discussed above. This is because for most luminosities, the high-mass end of the mass functions in Figure 2 is dominated by the exponential fall-off of the input mass function.
Second, at high luminosities, above  the effect of the AGN luminosity on the host galaxy mass function is to change the number of hosts, but not to change the peak mass or, to first order, the shape of the mass function. This is because of the steep exponential fall off in the input mass function of galaxies above
the effect of the AGN luminosity on the host galaxy mass function is to change the number of hosts, but not to change the peak mass or, to first order, the shape of the mass function. This is because of the steep exponential fall off in the input mass function of galaxies above  Above
Above  the peak host galaxy mass is always close to M∗ because there are so few more massive galaxies. The number of M∗ galaxies at the peak is determined by how high of Eddington ratios are required to bring these objects into the luminosity range in question. For these high AGN luminosities, the shape of the mass function of (SF) hosts is very similar to that of passive galaxies except that the faint end slope is significantly steeper (
the peak host galaxy mass is always close to M∗ because there are so few more massive galaxies. The number of M∗ galaxies at the peak is determined by how high of Eddington ratios are required to bring these objects into the luminosity range in question. For these high AGN luminosities, the shape of the mass function of (SF) hosts is very similar to that of passive galaxies except that the faint end slope is significantly steeper ( with
with  ) than that of the passive galaxies, which is given by
) than that of the passive galaxies, which is given by  (see Peng et al. 2010). In mathematical form, the mass function of galaxies at any AGN luminosity above L∗ will have a Schechter shape
(see Peng et al. 2010). In mathematical form, the mass function of galaxies at any AGN luminosity above L∗ will have a Schechter shape

At lower luminosities well below  the behavior changes and a region of intermediate slope appears. For black hole masses between
the behavior changes and a region of intermediate slope appears. For black hole masses between  and
and  the mass function will have the slope given by
the mass function will have the slope given by  At very low masses we will again always recover the slope of
At very low masses we will again always recover the slope of 
The location of the peak in the black hole mass function therefore depends on the slopes of both underlying distributions (Eddington ratio and galaxy mass function), i.e., on the sign of α + δ1. Not surprisingly, this intermediate zone also appears in the host galaxy mass function with the same slope. This produces a peak host galaxy mass of

This difference in behavior can be understood as follows: In the  case the dominant contribution to the luminosity function will come from low-mass object accretion at high Eddington ratios, which is more numerous than high-mass object accretion at low Eddington ratios. In the second case, the roles are simply reversed and the main contributor to the QLF will be high-mass AGNs with low Eddington ratios.
case the dominant contribution to the luminosity function will come from low-mass object accretion at high Eddington ratios, which is more numerous than high-mass object accretion at low Eddington ratios. In the second case, the roles are simply reversed and the main contributor to the QLF will be high-mass AGNs with low Eddington ratios.
If black hole masses were very tightly correlated with host galaxy masses, then clearly the same behavior would be seen in the black hole mass function(s) since these would always be a simple (mass-)scaling of the galaxy mass function(s). However, the effect of scatter in the black hole to host galaxy mass relation is quite marked. This is visible in Figure 2. The reason is clear: the mass function of black holes will now be much smoother than that of the host galaxies since the log normal scatter smooths out the sharp exponential drop of the galaxies at high masses (recall that Figure 2 used a 0.5 dex scatter). Of course, it might be argued that the black hole mass is somehow more fundamental, and that the galaxy mass function should be obtained by smoothing it. However, we know the galaxy mass function quite well, and it has an exponential cutoff (see Peng et al. 2010; Baldry et al. 2012). We do not, at this stage, know the underlying mass function of black holes in SF galaxies. With this scatter, there is a much smoother variation of the peak mass with AGN luminosity.
Figure 2. Expected shape of the black hole and the black hole host galaxy mass function, selected in different AGN luminosity bins. Mass is plotted relative to the Schechter M∗ of the galaxy population ( ) and Φ relative to the
) and Φ relative to the  of the galaxy population. All luminosities are relative to the L∗ of the AGN luminosity function. The black dashed line is connecting the masses where the mass functions reach maximum value.
of the galaxy population. All luminosities are relative to the L∗ of the AGN luminosity function. The black dashed line is connecting the masses where the mass functions reach maximum value.
Download figure:
Standard image High-resolution imageThe dashed lines show the variation of the peak mass with luminosity. The fact that the difference between these dashed curves on the two panels decreases with luminosity illustrates the well-known "Lauer effect" (Lauer et al. 2007) whereby the typical objects at high AGN luminosities will generally have been scattered above the mean black hole host mass relation. It should be noted, however, that there is no change in the low-mass slope of the mass function(s) due to scatter and this remains a very robust prediction of our model.
It is worth noting in Figure 2 that the peak of the black hole mass distribution varies quite weakly with luminosity, i.e., a change in luminosity of 1 dex is associated with a smaller increase in the peak mbh. This means that we will generally see higher Eddington ratios in higher luminosity quasars even though the Eddington ratio distribution is taken to be strictly independent of black hole mass. We return to this point in Section 6.1 below.
We stress that the (solid) curves in Figure 2 that show the mass functions of AGN host galaxies (with masses normalized to the Schechter M∗) at different AGN luminosities (computed relative to the knee of the luminosity function) are an easily testable prediction of the convolution approach, modulo the effects linked to the choice of α and δ1 discussed above, which can shift the peak of 
4. DATA
We next turn to demonstrating how our model relates to the observations of the mass function of SF galaxies and QLF. In this section, we will estimate the redshift evolution of parameters that describe these two populations.
4.1. Mass Function of Star-forming Galaxies
As explained previously, we need to know the mass function of SF galaxies to deduce the SMBH mass function in SF galaxies, ϕBH(mbh), which is an integral part of predicting the QLF in Equation (3). We also want to verify the predictions of Peng et al. (2010, 2012) for the time evolution of the parameters of the galaxy mass function (e.g., Equation (B3) from Peng et al. 2012).
In order to do this, we fit the data for SF galaxies from Ilbert et al. (2013) at all redshifts with a single Schechter function in which the parameters (
 ) are smoothly varying functions of redshift. Fitting all the data in this fashion, instead of fitting at single redshifts, enables us to follow better the evolution of the parameters. It also reduces the sensitivity to small variations that may compromise fits at a single redshift and add to the degeneracies between parameters. This procedure of simultaneously fitting all the data of the galaxy mass function at different redshifts is analogous to the standard procedure often used in determining the evolving QLF (e.g., Hopkins et al. 2007; Ueda et al. 2014). The functional form that we use for the redshift evolution of the galaxy mass function is
) are smoothly varying functions of redshift. Fitting all the data in this fashion, instead of fitting at single redshifts, enables us to follow better the evolution of the parameters. It also reduces the sensitivity to small variations that may compromise fits at a single redshift and add to the degeneracies between parameters. This procedure of simultaneously fitting all the data of the galaxy mass function at different redshifts is analogous to the standard procedure often used in determining the evolving QLF (e.g., Hopkins et al. 2007; Ueda et al. 2014). The functional form that we use for the redshift evolution of the galaxy mass function is

where we model the redshift dependence as

with  The slope of the low-mass end, αSF, was kept constant at the local value of αSF = −0.4 as there is considerable evidence that there is little or no change in the low-mass slope for the redshift range considered (Peng et al. 2014).
The slope of the low-mass end, αSF, was kept constant at the local value of αSF = −0.4 as there is considerable evidence that there is little or no change in the low-mass slope for the redshift range considered (Peng et al. 2014).
The evolution of parameters of mass function in Figure 3 confirms that M∗ is more or less constant up until at least redshift 2.5, i.e., it verifies the Ansätz of Peng et al. (2010), which establishes a single quenching mass scale M∗ that does not change with redshift. It is important to stress that our results will not depend critically on the exact functional evolution of M∗ above  but will use the by now well-established observational fact that M∗ does not change at
but will use the by now well-established observational fact that M∗ does not change at  and that the evolution in the galaxy population since that time is associated with a "vertical" evolution in
and that the evolution in the galaxy population since that time is associated with a "vertical" evolution in  We have also performed this analysis with the data set from Muzzin et al. (2013) and the compilation of galaxy mass functions from Behroozi et al. (2013b) and our conclusions presented in the rest of this paper do not change.
We have also performed this analysis with the data set from Muzzin et al. (2013) and the compilation of galaxy mass functions from Behroozi et al. (2013b) and our conclusions presented in the rest of this paper do not change.
Figure 3. Evolution of  and M∗ parameters in the Schecter mass function of star-forming galaxies. Data shows minimal evolution of M∗ until at least
and M∗ parameters in the Schecter mass function of star-forming galaxies. Data shows minimal evolution of M∗ until at least  2.5, but significant evolution in
2.5, but significant evolution in 
Download figure:
Standard image High-resolution image4.2. Quasar Luminosity Function
Hopkins et al. (2007) combined measurements of QLFs in different bands, fields, and redshifts in order to characterize the bolometric QLF at epochs  In their work, the best-fit luminosity-dependent bolometric correction and luminosity and redshift-dependent column density distributions are used in order to construct an estimate of the bolometric QLF, which should be consistent with all of the various individual surveys. Although now several years old, we believe that this synthesized QLF compilation remains the most comprehensive and is used as the basis of the current paper.
In their work, the best-fit luminosity-dependent bolometric correction and luminosity and redshift-dependent column density distributions are used in order to construct an estimate of the bolometric QLF, which should be consistent with all of the various individual surveys. Although now several years old, we believe that this synthesized QLF compilation remains the most comprehensive and is used as the basis of the current paper.
Table 1. Evolution of Star-forming Galaxy Mass Function, Data From Ilbert et al. (2013)
| Parameter | Fixed  = −0.4 = −0.4 |
|---|---|
| a0 | −2.55 ± 0.04 |
| a1 | −0.26 ± 0.06 |
| a2 | −1.6 ± 0.12 |
| a3 | −0.88 ± 0.16 |
| b0 | 10.9 ± 0.04 |
| b1 | −0.53 ± 0.11 |
| b2 | 3.36 ± 0.11 |
| b3 | −3.75 ± 0.13 |
Download table as: ASCIITypeset image
We proceed with fitting their tabulated data with a double power-law QLF, as given by Equation (1). We fit both at each redshift individually, and carry out a "full fit" where the parameters (i.e., 

 , and γ2) are all constrained to be smoothly varying functions of redshift, i.e., adopting a similar approach as we used earlier in our fitting of the galaxy mass function in Section 4.1. This "full" fitting of a redshift-dependent double power law is essentially the same as the approach used in Hopkins et al. (2007), with one important difference. In order to avoid degeneracies in the fits it is necessary, both here and in Hopkins et al. (2007), to fix one or more of the parameters. Hopkins et al. (2007) chose to require a redshift-independent
, and γ2) are all constrained to be smoothly varying functions of redshift, i.e., adopting a similar approach as we used earlier in our fitting of the galaxy mass function in Section 4.1. This "full" fitting of a redshift-dependent double power law is essentially the same as the approach used in Hopkins et al. (2007), with one important difference. In order to avoid degeneracies in the fits it is necessary, both here and in Hopkins et al. (2007), to fix one or more of the parameters. Hopkins et al. (2007) chose to require a redshift-independent  at a constant value. We now know that
at a constant value. We now know that  of the galaxy population changes significantly over the redshift range of interest and, as developed in the previous section, the relationship of
of the galaxy population changes significantly over the redshift range of interest and, as developed in the previous section, the relationship of  relative to
relative to  is of great interest in the context of the duty cycle. In contrast, γ1 is set, in our convolution model, by the low mass slope αSF of the mass function of SF galaxies. As mentioned before there is not much evidence (see Peng et al. 2014) that this changes significantly, if at all, over the redshift range of interest, nor compelling evidence for a change in γ1. Therefore, we choose to have a redshift-independent faint end slope of the luminosity function, γ1 and to allow
is of great interest in the context of the duty cycle. In contrast, γ1 is set, in our convolution model, by the low mass slope αSF of the mass function of SF galaxies. As mentioned before there is not much evidence (see Peng et al. 2014) that this changes significantly, if at all, over the redshift range of interest, nor compelling evidence for a change in γ1. Therefore, we choose to have a redshift-independent faint end slope of the luminosity function, γ1 and to allow  to vary with redshift. It should be noted that our fitting procedure is the same as a "luminosity and density evolution" model (e.g., Aird et al. 2010) except that we are allowing the bright end slope γ2 to vary. We do this because, as we have seen, γ2 is set by the high λ behavior of the Eddington ratio distribution ξ(λ).
to vary with redshift. It should be noted that our fitting procedure is the same as a "luminosity and density evolution" model (e.g., Aird et al. 2010) except that we are allowing the bright end slope γ2 to vary. We do this because, as we have seen, γ2 is set by the high λ behavior of the Eddington ratio distribution ξ(λ).
The parameters in the luminosity function are allowed to vary as

with again κ = log(1 + z). We follow Hopkins et al. (2007) in fitting γ1 and γ2 as a polynomial in z (rather than κ =log(1 + z)), but this choice is not of great importance.
Additional degrees of freedom were added to the fit until we can find no appreciable quantitative difference in the quality of the fit. The values of the double power-law parameters in the smoothly varying "full-fit" are given in Table 2 and the fits are shown with orange curves in Figure 4.
Figure 4. Fits to the bolometric data set compiled in Hopkins et al. (2007), with the broken power-law fit of Equation (1). The orange curve shows our "full fit" done with parametrization in Equation (18). The red curve shows the fit in which the redshift dependence of  is set to be exactly the redshift dependence of
is set to be exactly the redshift dependence of 
Download figure:
Standard image High-resolution imageTable 2. Best Fits to QLF Data from Hopkins et al. (2007)
| Parameter | "Full Fit" | With 
|
|---|---|---|
| c0 | −4.35 ± 0.06 | −1.79 ± 0.04 |
| c1 | 0.059 ± 0.07 | ⋯ |
| c2 | −3.2 ± 0.3 | ⋯ |
| c3 | 1.73 ± 0.2 | ⋯ |
| d0 | 44.67 ± 0.06 | 44.67 ± 0.04 |
| d1 | 4.02 ± 0.07 | 4.09 ± 0.09 |
| d2 | 3.78 ± 0.08 | 3.5 ± 0.07 |
| d3 | −4.68 ± 0.1 | −3.85 ± 0.07 |
| d4 | −5.7 ± 0.2 | −5.98 ± 0.15 |
| e0 | 0.5 ± 0.03 | 0.52 ± 0.04 |
| f0 | 1.64 ± 0.05 | 1.63 ± 0.06 |
| f1 | 0.54 ± 0.05 | 0.56 ± 0.06 |
| f2 | −0.12 ± 0.01 | −0.106 ± 0.03 |
Download table as: ASCIITypeset image
The redshift dependences of  and L∗ are shown in the panels of Figure 5 and we discuss these results in the next section.
and L∗ are shown in the panels of Figure 5 and we discuss these results in the next section.
Figure 5. Top left: redshift evolution of QLF parameters L∗ and  in our "full fit." The contours are showing 1-σ allowed regions of parameter space for fits that were made with data at each individual redshift. The filled circles are the result of a global fit, for which the resulting QLF is shown in Figure 4. Uncertainty contours for this fit are not shown here for clarity. Top right panel: projection showing explicitly the change of normalization
in our "full fit." The contours are showing 1-σ allowed regions of parameter space for fits that were made with data at each individual redshift. The filled circles are the result of a global fit, for which the resulting QLF is shown in Figure 4. Uncertainty contours for this fit are not shown here for clarity. Top right panel: projection showing explicitly the change of normalization  with redshift. Bottom left: projection showing explicitly the change of L∗ with redshift.
with redshift. Bottom left: projection showing explicitly the change of L∗ with redshift.
Download figure:
Standard image High-resolution imageFigure 6. Same as Figure 5 for the QLF fit at redshifts  in which we demanded that
in which we demanded that  i.e., that redshift dependence of these two variables is the same.
i.e., that redshift dependence of these two variables is the same.
Download figure:
Standard image High-resolution image5. RESULTS FROM COMPARING THE EVOLUTION OF THE QLF AND THE GALAXY MASS FUNCTION
5.1. The Evolution of 
The first result is that we notice a strong similarity between the observed redshift dependence of  in Figure 5 and the observed
in Figure 5 and the observed  in Figure 3. Both drop by ∼0.5 dex by redshift 2. Their relative evolution is explicitly compared in the bottom right panel of Figure 7, which shows that a constant ratio between
in Figure 3. Both drop by ∼0.5 dex by redshift 2. Their relative evolution is explicitly compared in the bottom right panel of Figure 7, which shows that a constant ratio between  and
and  is perfectly consistent with the data. We note that the fact that the density normalization of the QLF decreases slowly with redshift has been seen in several previous analyses, for instance in the "luminosity and density evolution" model of Aird et al. (2010), which has a 0.4 dex decrease in normalization between redshifts 0 and 2, and Croom et al. (2009) shows a very similar decrease of normalization in their "luminosity and density evolution" model, while Hasinger et al. (2005) show a decrease in normalization of 0.5 dex between redshift 0.6 and 2.4. Here we highlight the striking similarity of this behavior to the observed decline in
is perfectly consistent with the data. We note that the fact that the density normalization of the QLF decreases slowly with redshift has been seen in several previous analyses, for instance in the "luminosity and density evolution" model of Aird et al. (2010), which has a 0.4 dex decrease in normalization between redshifts 0 and 2, and Croom et al. (2009) shows a very similar decrease of normalization in their "luminosity and density evolution" model, while Hasinger et al. (2005) show a decrease in normalization of 0.5 dex between redshift 0.6 and 2.4. Here we highlight the striking similarity of this behavior to the observed decline in 
Figure 7. Top: comparison of the redshift evolution of the normalization of the star-forming galaxy mass function and the normalization of the quasar luminosity function. Black circles show the values of  that were determined by fitting the data from Ilbert et al. (2013) at a single redshift. Black squares show the values of
that were determined by fitting the data from Ilbert et al. (2013) at a single redshift. Black squares show the values of  that were determined by fitting the QLF data at a single redshift and are also shown in Figures5 and 6. Bottom: redshift evolution of the
that were determined by fitting the QLF data at a single redshift and are also shown in Figures5 and 6. Bottom: redshift evolution of the  This ratio is remarkably constant over the redshift range for which data is available.
This ratio is remarkably constant over the redshift range for which data is available.
Download figure:
Standard image High-resolution imageReferring back to Section 3.3, a constant ratio between  and
and  implies a constant duty cycle of the black holes in the context of our convolution model. To explore this further, we now repeat the fitting procedure but set the evolution of
implies a constant duty cycle of the black holes in the context of our convolution model. To explore this further, we now repeat the fitting procedure but set the evolution of  to be exactly that of
to be exactly that of  i.e., we impose that the evolution of the QLF normalization is the same as the evolution of the normalization of SF galaxies in the redshift range where we have
i.e., we impose that the evolution of the QLF normalization is the same as the evolution of the normalization of SF galaxies in the redshift range where we have  available (z < 3.5), while the constant multiplicative offset between these parameters remains a free parameter to be determined by the fitting procedure, i.e.,
available (z < 3.5), while the constant multiplicative offset between these parameters remains a free parameter to be determined by the fitting procedure, i.e.,

The results of this fitting are given in Tableapj519757t2 2 and the resulting QLF is shown with the red curve in Figure 4. It can be seen that the fit is extremely good, being only marginally worse then the full fit of Hopkins et al. (2007) (χ2this work/dof = 2.1; χ2Hopkins/dof=2.0), both of which have the comparable number of free parameters. The main driver for the slightly worse fits in our work is the deviation of the fit from data for low luminosities at low redshifts. The data in this regime may be contaminated by contributions from the stellar populations of the hosts, as discussed in Hopkins et al. (2007).
The parameter evolution in this " -matched" fitting is shown as linked filled circles in Figure 6. As one can see, the points are typically situated on the edges of the individual 1-σ contours, which is to be expected given that χ2/dof = 2.1. We conclude that the change of normalization of the QLF is perfectly consistent with the change of normalization of the SF galaxy mass function over the entire redshift range for which we have the measurements of normalization of the SF galaxy mass function.
-matched" fitting is shown as linked filled circles in Figure 6. As one can see, the points are typically situated on the edges of the individual 1-σ contours, which is to be expected given that χ2/dof = 2.1. We conclude that the change of normalization of the QLF is perfectly consistent with the change of normalization of the SF galaxy mass function over the entire redshift range for which we have the measurements of normalization of the SF galaxy mass function.
The fact that as far as we can tell the  and
and  track each other throughout cosmic time (at least since z ∼ 3, and quite possibly since earlier epochs also, is an interesting result. It means that the factor connecting these two quantities, which in the convolution model is
track each other throughout cosmic time (at least since z ∼ 3, and quite possibly since earlier epochs also, is an interesting result. It means that the factor connecting these two quantities, which in the convolution model is  (slightly modified by Δϕ), remains constant.
(slightly modified by Δϕ), remains constant.
As we have discussed above, this suggests that the general "duty cycle," fd, stays constant over cosmic time (e.g., Equations (8) and (11); see also Conroy & White 2013). Clearly, this would not be the case for other definitions of "duty cycle" that are based, for instance, on the fraction of black holes radiating above some luminosity or accreting above some Eddington ratio, if  or L∗ evolves with time, as it does (see below), but we believe that our definition of duty cycle is the most natural one (as discussed above).
or L∗ evolves with time, as it does (see below), but we believe that our definition of duty cycle is the most natural one (as discussed above).
5.2. The Evolution of 
The other striking feature of the QLF is the strong redshift evolution of  which increases by almost two orders of magnitude back to z ∼ 2. At higher redshifts, the
which increases by almost two orders of magnitude back to z ∼ 2. At higher redshifts, the  certainly flattens out and probably declines, although this cannot be established at high significance. The strong initial rise with redshift is seen independent of whether we use the full fit, or the fit constrained to have
certainly flattens out and probably declines, although this cannot be established at high significance. The strong initial rise with redshift is seen independent of whether we use the full fit, or the fit constrained to have  and
and  tracking each other.
tracking each other.
In our convolution model, the steep rise in  (see Equation (13)) could have been caused in principle by one or more of (a) an evolution of
(see Equation (13)) could have been caused in principle by one or more of (a) an evolution of  (b) an evolution of M∗ of the galaxy mass function, or (c) an evolution of the mass ratio
(b) an evolution of M∗ of the galaxy mass function, or (c) an evolution of the mass ratio 
As discussed in Section 4.1, we know that the characteristic M∗ of the galaxy population does not change, especially in the redshift range where increase of L∗ is most prominent (z ≤ 2), so case (b) will not apply. There is however complete degeneracy between cases (a) and (c), i.e., the distribution of specific accretion rates of AGNs and black holes to stellar mass ratio. This is clear in Equation (13) and as has been pointed out by, e.g., Veale et al. (2014). This degeneracy can only be broken if we have information on the black hole masses of the AGN. We will explore this in the next section of the paper.
6. TESTING THE MODEL WITH BLACK HOLE MASS DATA
6.1. The Quasar Mass–Luminosity Plane
In this part of the paper we will compare predictions of how the black hole mass–luminosity plane of broad-line AGNs should be populated in our model, and compare these with SDSS data. After creating a mock sample of SF galaxies in an SDSS volume, we will populate them with black holes assuming different redshift-dependent  scaling relations and an assumed scatter. We will then assign Eddington ratios from the evolving
scaling relations and an assumed scatter. We will then assign Eddington ratios from the evolving  distribution and apply an obscuration prescription from Hopkins et al. (2007). These two functions are chosen so that the QLF is reproduced as in the previous section: in other words the redshift evolution in
distribution and apply an obscuration prescription from Hopkins et al. (2007). These two functions are chosen so that the QLF is reproduced as in the previous section: in other words the redshift evolution in  and the redshift evolution in
and the redshift evolution in  must combine to produce the observed evolution in the QLF
must combine to produce the observed evolution in the QLF 
For the observational distribution, we use data from two observational studies (Shen et al. 2011; Trakhtenbrot & Netzer 2012) to show that our results do not depend critically on the data choice and to give the reader a graphical impression of the uncertainties involved in this kind of measurement. By comparing our mock data with the observed distribution we will be able to see which combination of redshift-dependent  and
and  best reproduces the observational data. We take into account the obscuration factor and the differences in bolometric correction between different works and apply the same bolometric correction to the data and model (namely one used in Shen et al. 2011) to make them directly comparable.
best reproduces the observational data. We take into account the obscuration factor and the differences in bolometric correction between different works and apply the same bolometric correction to the data and model (namely one used in Shen et al. 2011) to make them directly comparable.
By using this mock sample approach we can fully account for biases introduced by the luminosity selection of the quasar samples. We recreate data only up to z = 2, as black hole mass estimates for higher redshifts are based on the broad C iv emission line, which was shown to be far less reliable for these purposes (Shen et al. 2008; Trakhtenbrot & Netzer2, and references therein).
We first show in the topmost panels of the Figure 8 the modeled distribution of quasars in the black hole mass–luminosity (mbh, L) plane in three representative redshift bins if we assume a redshift-independent  with the standard value of
with the standard value of  We introduce a log-normal scatter in this relationship of 0.5 dex to account for scatter in the
We introduce a log-normal scatter in this relationship of 0.5 dex to account for scatter in the  relationship. The solid diagonal line indicates the Eddington limit (
relationship. The solid diagonal line indicates the Eddington limit ( ).
).
Figure 8. Mass–luminosity plane shown in three representative redshift bins. Our model with assumed non-evolving relation  is in the top row and our model with assumed evolving relation
is in the top row and our model with assumed evolving relation  is in the row below. Observational data from Shen et al. (2011) and Trakhtenbrot & Netzer (2012) are shown in bottom two rows. The thick black line is the Eddington limit, dashed orange lines show the calculated luminosity selection limit for the lowest and highest redshifts in the bin. The dotted and dashed black lines represent FWHM = 1000 km s−1 and 1500 km s−1, respectively, and are shown here to indicate which objects could be missed in observations because of the FWHM limit in quasar selection. Contours are set at
is in the row below. Observational data from Shen et al. (2011) and Trakhtenbrot & Netzer (2012) are shown in bottom two rows. The thick black line is the Eddington limit, dashed orange lines show the calculated luminosity selection limit for the lowest and highest redshifts in the bin. The dotted and dashed black lines represent FWHM = 1000 km s−1 and 1500 km s−1, respectively, and are shown here to indicate which objects could be missed in observations because of the FWHM limit in quasar selection. Contours are set at  20% etc., values of estimated probability distribution of the objects. Outermost objects are represented as individual dots.
20% etc., values of estimated probability distribution of the objects. Outermost objects are represented as individual dots.
Download figure:
Standard image High-resolution imageThe data from (Shen et al. 2011; Trakhtenbrot & Netzer 2012) are plotted in the two bottom rows of panels in Figure 8. In these panels, the diagonal dashed and dotted lines indicate the locus of black hole masses for two constant FWHMs (of 1000 km s−1 and 1500 km s−1, respectively) of the emission lines (Hβ and Mg ii) that were used to infer the black hole masses. Systems of lower FWHM will not appear in the samples, e.g., the limit used in Shen et al. (2011) is set at 1200 km s−1.
We see that, although there is good agreement at low redshifts, a non-evolving  relation produces far too many objects with masses that are too small or, equivalently, which have very high Eddington ratios, with around 50% being super-Eddington in the final redshift bin, while only around 2% of objects are super-Eddington in the data. This is a simple consequence of the fact that L∗ is much higher than locally and is a reflection of the high
relation produces far too many objects with masses that are too small or, equivalently, which have very high Eddington ratios, with around 50% being super-Eddington in the final redshift bin, while only around 2% of objects are super-Eddington in the data. This is a simple consequence of the fact that L∗ is much higher than locally and is a reflection of the high  implied for an unevolving
implied for an unevolving  relation shown in Figure 17.
relation shown in Figure 17.
It should be noted that the problem gets worse if we reduce the scatter in the  relation, as we then have even fewer high-mass black holes. We note that the comparison could not be expected to be perfect because our data is constrained to reproduce the QLF from Hopkins et al. (2007); although SDSS data and the optical QLF is the main contributor to the Hopkins QLF in this luminosity range, there are small contributions from other surveys as well as slightly different bolometric and obscuration corrections that will induce small differences. Nevertheless, the disagreement with a non-evolving
relation, as we then have even fewer high-mass black holes. We note that the comparison could not be expected to be perfect because our data is constrained to reproduce the QLF from Hopkins et al. (2007); although SDSS data and the optical QLF is the main contributor to the Hopkins QLF in this luminosity range, there are small contributions from other surveys as well as slightly different bolometric and obscuration corrections that will induce small differences. Nevertheless, the disagreement with a non-evolving  ratio is too large to be due to this.
ratio is too large to be due to this.
A much better agreement is obtained (second row of Figure 8) if we adopt an evolving  relation. We adopt as a heuristic example the form
relation. We adopt as a heuristic example the form  with n = 2. The agreement with the observed distribution is considerably better and there are now far fewer objects crossing the Eddington limit (∼3%) at high redshifts. This means that the observed
with n = 2. The agreement with the observed distribution is considerably better and there are now far fewer objects crossing the Eddington limit (∼3%) at high redshifts. This means that the observed  increase in
increase in  back to
back to  would be due to an equal split between a
would be due to an equal split between a  change in
change in  and a
and a  change in characteristic Eddington ratio
change in characteristic Eddington ratio  remembering that these two changes are degenerate in our convolution model without the
remembering that these two changes are degenerate in our convolution model without the  data of Figure 8.
data of Figure 8.
Finally we note that, quite independently of any assumptions about  our convolution model naturally recreates the apparent "sub-Eddington boundary" that has been emphasized by Steinhardt & Elvis (2010b), by which we mean the flat upper envelope. This refers to the fact that at all redshifts there seems to be a lack of objects at high masses close to the Eddington limit, which can also be seen in Figure 16 of Trakhtenbrot & Netzer (2012). This can be observed in Figure 8 where the upper contours of the red regions have slopes that are noticeably shallower than the 45° slope that corresponds to a constant Eddington ratio, thereby giving the impression of an absence of high-luminosity high λ sources.
our convolution model naturally recreates the apparent "sub-Eddington boundary" that has been emphasized by Steinhardt & Elvis (2010b), by which we mean the flat upper envelope. This refers to the fact that at all redshifts there seems to be a lack of objects at high masses close to the Eddington limit, which can also be seen in Figure 16 of Trakhtenbrot & Netzer (2012). This can be observed in Figure 8 where the upper contours of the red regions have slopes that are noticeably shallower than the 45° slope that corresponds to a constant Eddington ratio, thereby giving the impression of an absence of high-luminosity high λ sources.
This behavior is quite counterintuitive, and was interpreted by Steinhardt & Elvis (2010b) as being caused by some new physical effect that somehow limits accretion onto more luminous quasars. Various authors have proposed alterations to the measurement methods in the mass–luminosity plane, which could reduce or eliminate this effect (e.g., Rafiee & Hall 2011a, 2011b). We show instead that this behavior is actually expected from the convolution model presented in this paper!
We commented earlier in Section 3.4 that while the typical black hole mass increases with luminosity in our convolution model, it does so sub-linearly, so that the "typical" Eddington ratio must also increase with luminosity. This can be seen also in these plots: the ridge line that is defined by the peak in the mass distributionat a given L is indeed steeper than the 45° line of constant Eddington ratio, which is why the shallower slope of the boundary defined by the contours is so counterintuitive. However, because the number of more massive black holes falls very steeply with mass, because of the decline of the galactic mass function above  the contours of constant surface density, given by the contours in the plots in Figure 8 and in the Steinhardt & Elvis (2010b) analysis, are actually shallower than the 45° line.
the contours of constant surface density, given by the contours in the plots in Figure 8 and in the Steinhardt & Elvis (2010b) analysis, are actually shallower than the 45° line.
This is more clearly seen in Figure 9 were we show the appearance of our full sample, before the application of the SDSS luminosity cut. At lower luminosities the effect gets more and more pronounced and we expect that deeper surveys of a given area would find more super-Eddington objects at small masses.
Figure 9. Full sample from our model, before applying the luminosity cuts to produce the second row in Figure 8. For clarity, only 1 out of every 25 points is shown.
Download figure:
Standard image High-resolution imageFigure 10. Top left: resulting  relation in quenched galaxy systems today, if we only take into account systems that have quenched after z = 2. The orange line shows best fit quoted in Kormendy & Ho (2013). The blue line shows best fit to the data generated from 40 realizations of the model. Top right: resulting
relation in quenched galaxy systems today, if we only take into account systems that have quenched after z = 2. The orange line shows best fit quoted in Kormendy & Ho (2013). The blue line shows best fit to the data generated from 40 realizations of the model. Top right: resulting  relation in quenched systems today, for full range of quenching history (
relation in quenched systems today, for full range of quenching history ( ). The orange and blue lines are generated in the same way as in the previous panel. Merging, uncertain evolution in the
). The orange and blue lines are generated in the same way as in the previous panel. Merging, uncertain evolution in the  relation, and errors in the estimated rate of quenching at high redshift could bias this result, as discussed in the text. Bottom left: measured
relation, and errors in the estimated rate of quenching at high redshift could bias this result, as discussed in the text. Bottom left: measured  by Kormendy & Ho (2013). The orange line shows again the best fit quoted in Kormendy & Ho (2013). Bottom right: measured
by Kormendy & Ho (2013). The orange line shows again the best fit quoted in Kormendy & Ho (2013). Bottom right: measured  by Häring & Rix (2004).
by Häring & Rix (2004).
Download figure:
Standard image High-resolution imageWe emphasize that the reproduction of the Steinhardt & Elvis (2010b) effect in Figure 8 is achieved within our convolution model with an Eddington ratio distribution  that is completely independent of black hole mass. The effect noted by Steinhardt & Elvis (2010b) would not be seen (in our model) if the distribution of points in the
that is completely independent of black hole mass. The effect noted by Steinhardt & Elvis (2010b) would not be seen (in our model) if the distribution of points in the  plane was normalized to the total number of black holes (in SF galaxies) at a given mass, which is, of course, unfortunately not observable. Our explanation for the sub-Eddington boundary in Steinhardt & Elvis (2010b) is therefore a kind of "plotting bias" arising from what is plotted, rather than a "selection effect" per se, coming through the construction of the sample via, e.g., emission line widths.
plane was normalized to the total number of black holes (in SF galaxies) at a given mass, which is, of course, unfortunately not observable. Our explanation for the sub-Eddington boundary in Steinhardt & Elvis (2010b) is therefore a kind of "plotting bias" arising from what is plotted, rather than a "selection effect" per se, coming through the construction of the sample via, e.g., emission line widths.
6.2. Establishing the  Correlation in Quenched Systems
Correlation in Quenched Systems
In this section we show how it is possible to reproduce the observed tight correlation between  in the local universe even if the black hole to stellar mass relation in the SF galaxies is strongly evolving (see also Croton 2006; Hopkins et al. 2006a). In what follows, we loosely equate mbulge with the stellar mass of an SF galaxy when star formation quenches, which is also the point at which we assume that the black hole ceases growing. Readers uncomfortable with making this association may simply substitute mbulge in what follows with mquench.
in the local universe even if the black hole to stellar mass relation in the SF galaxies is strongly evolving (see also Croton 2006; Hopkins et al. 2006a). In what follows, we loosely equate mbulge with the stellar mass of an SF galaxy when star formation quenches, which is also the point at which we assume that the black hole ceases growing. Readers uncomfortable with making this association may simply substitute mbulge in what follows with mquench.
For this analysis, we use results from the simple galaxy evolution model of Birrer et al. (2014) to construct a set of evolving SF galaxies and their quenched descendants. The details of the Birrer et al. (2014) model are not important for the present purpose since it reproduces well the overall evolution of the galaxy population, which is all that we require here.
For each quenched galaxy seen in the model at the present epoch, we know the mass and redshift at which it quenched and can therefore compute the black hole mass from the adopted redshift-dependent  relation for (SF) galaxies, adding also the adopted scatter. We assume that there is no stellar mass growth after quenching and that there is no central SMBH mass growth after quenching.
relation for (SF) galaxies, adding also the adopted scatter. We assume that there is no stellar mass growth after quenching and that there is no central SMBH mass growth after quenching.
After this procedure we are left with a mock sample of quenched galaxies, with their black hole masses known, after which we can account for sample selection effects. This is not trivial, as measurements of masses of black holes are from heterogeneous sources and no single luminosity or other cut is possible.
We therefore decided to create an empirical selection in galaxy mass so that the distribution of galaxy masses in the mock sample broadly matches that of the passive early-type galaxies that have had their SMBH mass measured. We show results for two situations, where we first only consider galaxies that quenched after z = 2 and then include all galaxies that have quenched since z = 5. We differentiate between these two cases since we expect merging, which is not explicitly accounted for here, to have a larger impact for galaxies that quench earlier, and because the assumed mass ratio scaling, which we think is a reasonable approximation (see above) at redshift  may break down at higher redshifts. When we ignore quenching at
may break down at higher redshifts. When we ignore quenching at  we are losing only about 10% of today's quenched population, but the model is on a much firmer footing.
we are losing only about 10% of today's quenched population, but the model is on a much firmer footing.
We have fitted the simulated data, derived from 40 random realizations of the model, with a relation of the form

by regressing the black hole mass on the stellar mass, and compute the scatter of the simulated galaxies around this relation. We derive values of  and a scatter of 0.53 dex for the case of quenching only from z = 2, and values of
and a scatter of 0.53 dex for the case of quenching only from z = 2, and values of  with a scatter of 0.6 dex for the case of quenching from z = 5. These values should be compared with the observed values of
with a scatter of 0.6 dex for the case of quenching from z = 5. These values should be compared with the observed values of  and an intrinsic scatter of 0.29 dex derived in Kormendy & Ho (2013). While the predicted scatter appears to be slightly larger than observed, subsequent merging of galaxies, which has not been modeled here, will act to reduce the scatter (Hirschmann et al. 2010; Jahnke & Macciò 2011).
and an intrinsic scatter of 0.29 dex derived in Kormendy & Ho (2013). While the predicted scatter appears to be slightly larger than observed, subsequent merging of galaxies, which has not been modeled here, will act to reduce the scatter (Hirschmann et al. 2010; Jahnke & Macciò 2011).
The origin of the  relation is the underlying
relation is the underlying  relation in the SF galaxies assumed in the model, with added scatter due to the fact that galaxies of a given stellar mass today have quenched at various redshifts and, for a given stellar mass, the spread in black hole masses is amplified by the spread in the quenching redshifts. The mean of the
relation in the SF galaxies assumed in the model, with added scatter due to the fact that galaxies of a given stellar mass today have quenched at various redshifts and, for a given stellar mass, the spread in black hole masses is amplified by the spread in the quenching redshifts. The mean of the  relation is positioned roughly at the value of
relation is positioned roughly at the value of  at the mean redshift of quenching at that mass, which is
at the mean redshift of quenching at that mass, which is  over a wide range of galaxy masses.
over a wide range of galaxy masses.
It is interesting to note that objects that have quenched more recently would be expected on average to have a lower  value, because of the evolution in
value, because of the evolution in  It is possible that these recently quenched galaxies could be associated with pseudo-bulges instead of bulges. Kormendy & Ho (2013) has indeed argued that pseudo-bulges do indeed have a lower
It is possible that these recently quenched galaxies could be associated with pseudo-bulges instead of bulges. Kormendy & Ho (2013) has indeed argued that pseudo-bulges do indeed have a lower  ratio.
ratio.
We also note in passing that if there is a trend for the typical quenching redshift to increase with increasing stellar mass (e.g., because of interplay of mass and environment quenching, Peng et al. 2010) then this would introduce a tilt in the local  relation (
relation ( ) even though the input
) even though the input  in SF galaxies was perfectly linear.
in SF galaxies was perfectly linear.
The link with quenching redshift then prompts another interesting point. There is very good evidence that the sizes of galaxies, at a given mass, are smaller at high redshift (Daddi et al. 2005; Newman et al. 2012; Carollo et al. 2013; Shankar et al. 2013a). We would therefore expect, through virial arguments, that the velocity dispersions, at a given mass, would also be higher. This has been directly observed in a few cases (e.g., van Dokkum et al. 2014). For analytic simplicity, we assume that the scale radius of galaxies scales as  so that the usual Faber–Jackson-type scaling relation would be expected to evolve as
so that the usual Faber–Jackson-type scaling relation would be expected to evolve as

If  scales as
scales as  as we have been exploring in this part of the paper, then this naturally produces an
as we have been exploring in this part of the paper, then this naturally produces an  relation that is independent of redshift.
relation that is independent of redshift.
This has two implications: first, we would not expect to see any significant evolution in the observed  relation (see, e.g., recently Shen et al. 2015). Second, we would expect the present-day
relation (see, e.g., recently Shen et al. 2015). Second, we would expect the present-day  relation for passive galaxies to be tighter than the
relation for passive galaxies to be tighter than the  relation because of the aforementioned broadening of the latter from the range of zquench.
relation because of the aforementioned broadening of the latter from the range of zquench.
We stress that this tighter  relation would be present even if the velocity dispersion is not playing a direct role in the growth of black holes. Of course, it is also possible that the evolution in the
relation would be present even if the velocity dispersion is not playing a direct role in the growth of black holes. Of course, it is also possible that the evolution in the  is in fact caused by the constancy of an underlying
is in fact caused by the constancy of an underlying  causal connection. On the other hand, there could well be other causes for
causal connection. On the other hand, there could well be other causes for  to evolve as
to evolve as  in which case the tight
in which case the tight  relation would simply be a coincidence.
relation would simply be a coincidence.
6.3.
 in AGNs in the Local Universe
in AGNs in the Local Universe
Finally, we turn to estimates of the  relations for AGNs in the local universe, where it is possible to estimate independently the mass of the galaxy that is hosting an optically active AGN. Matsuoka et al. (2014) made a careful decomposition into nuclear and host contributions of the images of
relations for AGNs in the local universe, where it is possible to estimate independently the mass of the galaxy that is hosting an optically active AGN. Matsuoka et al. (2014) made a careful decomposition into nuclear and host contributions of the images of  quasars in the SDSS Stripe 82. They found that the quasars are predominately hosted in massive SF galaxies, with relatively large
quasars in the SDSS Stripe 82. They found that the quasars are predominately hosted in massive SF galaxies, with relatively large  ratios of around
ratios of around  Matsuoka et al. (2014) were aware of the possibility that selection effects could bias this value upward but could not estimate their magnitude. We can now use our model to examine the expected size of this bias.
Matsuoka et al. (2014) were aware of the possibility that selection effects could bias this value upward but could not estimate their magnitude. We can now use our model to examine the expected size of this bias.
To do this we simulate sources within the same sky area as Stripe 82 and recreate objects above the AGN luminosity cut that would have been selected for quasar spectroscopy in the SDSS sample, with a scatter of  dex. The results are shown in Figure 11, represented in the same way as in the original paper. We see that the observed quasars will have
dex. The results are shown in Figure 11, represented in the same way as in the original paper. We see that the observed quasars will have  ratios that are indeed much higher than the mean value in the underlying sample, which is indicated by the shaded region in the figure.
ratios that are indeed much higher than the mean value in the underlying sample, which is indicated by the shaded region in the figure.
Figure 11. Top panel: simulated observation of  relation in Stripe 82, mimicking the analysis of Matsuoka et al. (2014). The blue line shows the mean
relation in Stripe 82, mimicking the analysis of Matsuoka et al. (2014). The blue line shows the mean  relation in the full sample (before the luminosity cut was applied), while the shaded area shows a
relation in the full sample (before the luminosity cut was applied), while the shaded area shows a  spread around the mean relation in our model. The black line shows the mean and spread of distribution of points in 0.1 redshift slices. The red line is set to
spread around the mean relation in our model. The black line shows the mean and spread of distribution of points in 0.1 redshift slices. The red line is set to  which is approximately the local relation from Häring & Rix (2004). Bottom panel: original data from Matsuoka et al. (2014).
which is approximately the local relation from Häring & Rix (2004). Bottom panel: original data from Matsuoka et al. (2014).
Download figure:
Standard image High-resolution imageFinally, we notice that even though we inserted the  redshift evolution in our model, this evolution would be quite hard to detect in the sample of Matsuoka et al. (2014), owing to the large spread of points and the selection biases connected with such a study. Nevertheless, we do still see a slight change in the mean values of the simulated sample that is not seen in the actual data. We discuss this further in Section 7.2 below.
redshift evolution in our model, this evolution would be quite hard to detect in the sample of Matsuoka et al. (2014), owing to the large spread of points and the selection biases connected with such a study. Nevertheless, we do still see a slight change in the mean values of the simulated sample that is not seen in the actual data. We discuss this further in Section 7.2 below.
7. DISCUSSION
In the preceding sections of this paper we have developed a simple generic model for obtaining the evolving AGN luminosity function from a convolution of the evolving galaxy mass function. This generic model makes testable predictions for quantities such as the shape of the mass distribution of host galaxies as a function of AGN luminosity and allows us to derive quantitative connections between the parameters describing the galaxy mass function and the AGN QLF. On the basis of these, we can derive powerful statements about the duty cycle of AGNs. We then showed, in the framework of this general model, that a redshift-dependent  and Eddington ratio distribution,
and Eddington ratio distribution,  successfully reproduces the observed QLF (by construction) and also reproduces observations of the distribution of quasars in the (
successfully reproduces the observed QLF (by construction) and also reproduces observations of the distribution of quasars in the ( ) plane, the black hole to bulge mass relation of quenched galaxies and measurements of
) plane, the black hole to bulge mass relation of quenched galaxies and measurements of  for low-redshift AGNs. In this section, we develop further some of the astrophysical implications of the preceding results.
for low-redshift AGNs. In this section, we develop further some of the astrophysical implications of the preceding results.
7.1. Comparing  Redshift Evolution in Active and Quenched Systems
Redshift Evolution in Active and Quenched Systems
It is important to appreciate that a quite rapid evolution in  in active (SF) AGN systems does not imply an equally rapid evolution of
in active (SF) AGN systems does not imply an equally rapid evolution of  in the quenched systems. This is because, when we are observing quenched systems, we are effectively observing the integrated history of previous activity. To illustrate this, we perform a simple heuristic exercise in which we determine
in the quenched systems. This is because, when we are observing quenched systems, we are effectively observing the integrated history of previous activity. To illustrate this, we perform a simple heuristic exercise in which we determine  in quenched systems at a given epoch, assuming as above that quenching started at redshift 2. We make the same assumptions as before, namely that there is no stellar or black hole mass growth after quenching.
in quenched systems at a given epoch, assuming as above that quenching started at redshift 2. We make the same assumptions as before, namely that there is no stellar or black hole mass growth after quenching.
Our results are shown in Figure 12. Even though SF galaxies have changed their black hole to stellar mass ratio by almost a factor of 10 from redshift  to today, the evolution in this ratio for quenched systems is much milder, more like a factor of 3 or even less (0.4 dex), simply because the quenched population includes galaxies that have quenched much earlier. This means that the redshift evolution in
to today, the evolution in this ratio for quenched systems is much milder, more like a factor of 3 or even less (0.4 dex), simply because the quenched population includes galaxies that have quenched much earlier. This means that the redshift evolution in  for quenched systems will always be much milder than the evolution in this quantity in active systems.
for quenched systems will always be much milder than the evolution in this quantity in active systems.
Figure 12. Evolution of the mean  relation in star-forming (heavy blue line) and quenched systems (heavy red line). The dashed blue line shows the redshift range where this mean relation may not accurately represent star-forming galaxies, as discussed in Section 7.2. The evolution in
relation in star-forming (heavy blue line) and quenched systems (heavy red line). The dashed blue line shows the redshift range where this mean relation may not accurately represent star-forming galaxies, as discussed in Section 7.2. The evolution in  for the quenched (inactive nuclei) galaxies is always shallower than for the population of actively accreting systems, potentially leading to an underestimate of the evolution if the populations are mixed. On the other hand, the "Lauer effect" will bias the
for the quenched (inactive nuclei) galaxies is always shallower than for the population of actively accreting systems, potentially leading to an underestimate of the evolution if the populations are mixed. On the other hand, the "Lauer effect" will bias the  upward in luminosity-selected active samples, which goes in the opposite direction. This is indicated by the thin black lines, which show the observed
upward in luminosity-selected active samples, which goes in the opposite direction. This is indicated by the thin black lines, which show the observed  for active systems for luminosity selection (labeled relative to L∗) for our standard assumption of σ = 0.5 dex.
for active systems for luminosity selection (labeled relative to L∗) for our standard assumption of σ = 0.5 dex.
Download figure:
Standard image High-resolution imageThe distinction between active and passive populations becomes even more important if observational studies compare actively accreting systems at high redshift with data on the quiescent population at low redshift. This is unfortunately a quite common practice (e.g., Jahnke et al. 2009; Decarli et al. 2010; Merloni et al. 2010; Bennert et al. 2011; Schramm & Silverman 2013; Schulze et al. 2015) because of the current practicalities of observations. We stress that this approach automatically produces weaker evolution since neither mbh nor m* will have changed once a given object becomes inactive (i.e., passive/quenched). It is therefore clear that the mean  relation in the quenched systems will reflect the mass ratio in the SF galaxies at the much earlier epochs when those galaxies actually quenched (as already discussed above). For the local population, this is typically around z ∼ 1–1.5.
relation in the quenched systems will reflect the mass ratio in the SF galaxies at the much earlier epochs when those galaxies actually quenched (as already discussed above). For the local population, this is typically around z ∼ 1–1.5.
Clearly, if we compare the  of SF systems at z ∼ 1–1.5 to the
of SF systems at z ∼ 1–1.5 to the  ratio of passive galaxies seen today that quenched at z ∼ 1–1.5, then we would expect to see no change in
ratio of passive galaxies seen today that quenched at z ∼ 1–1.5, then we would expect to see no change in  even if this ratio had changed a lot within the actively accreting population! Of course, if the high-redshift active systems are luminosity-selected, then their
even if this ratio had changed a lot within the actively accreting population! Of course, if the high-redshift active systems are luminosity-selected, then their  ratio will likely have been biased to higher values than the underlying population through the "Lauer effect" discussed in Section 3.4, which goes in the opposite direction (as shown by the parallel black lines in Figure 12). This figure shows that if nature has an underlying
ratio will likely have been biased to higher values than the underlying population through the "Lauer effect" discussed in Section 3.4, which goes in the opposite direction (as shown by the parallel black lines in Figure 12). This figure shows that if nature has an underlying  scaling as
scaling as  for active systems, then we would expect to see
for active systems, then we would expect to see  if we compare comparisons of active systems at
if we compare comparisons of active systems at  with quenched systems at
with quenched systems at  once we correct for these observational biases. This is quite similar to the evolution seen in at least some of the observational studies cited above (e.g., Jahnke et al. 2009; Decarli et al. 2010; Merloni et al. 2010; Schramm & Silverman 2013; Schulze et al. 2015).
once we correct for these observational biases. This is quite similar to the evolution seen in at least some of the observational studies cited above (e.g., Jahnke et al. 2009; Decarli et al. 2010; Merloni et al. 2010; Schramm & Silverman 2013; Schulze et al. 2015).
We have already commented in Section 6.2 that we would also expect to see little or no evolution in  for any population of galaxies, however selected. This is due to the higher σ associated with a given stellar mass at high redshift, which cancels out the
for any population of galaxies, however selected. This is due to the higher σ associated with a given stellar mass at high redshift, which cancels out the  dependence in
dependence in 
7.2. Mass Growth of Star-forming Galaxies at Low Redshift
In this paper we have made the conventional assumption that the black hole to stellar mass relation increases as some power of (1 + z), i.e.,  However, this is an arbitrary redshift dependence, and there are reasons why it cannot hold (with
However, this is an arbitrary redshift dependence, and there are reasons why it cannot hold (with  ) at low redshifts (see also Hopkins et al. 2006b). Assuming that an SF galaxy is on the Main Sequence we can track the increase of its stellar mass using the Main Sequence sSFR(z),
) at low redshifts (see also Hopkins et al. 2006b). Assuming that an SF galaxy is on the Main Sequence we can track the increase of its stellar mass using the Main Sequence sSFR(z),

where rsSFR is the "reduced specific star formation rate" (see Lilly et al. 2013),  where R is the fraction R of the stellar mass that is returned during star formation
where R is the fraction R of the stellar mass that is returned during star formation  which is therefore the inverse mass doubling timescale of the stellar population. Using
which is therefore the inverse mass doubling timescale of the stellar population. Using  Gyr−1 from Lilly et al. (2013) and references therein, this can be integrated to give
Gyr−1 from Lilly et al. (2013) and references therein, this can be integrated to give

This modest increase in stellar mass for an SF galaxy sets a maximal change in  ratio even in the most extreme case in which mbh does not increase at all. We show this maximal evolution in Figure 13 and compare it with the
ratio even in the most extreme case in which mbh does not increase at all. We show this maximal evolution in Figure 13 and compare it with the  evolution used elsewhere in the paper. It can be seen that the maximal evolution is actually slower than
evolution used elsewhere in the paper. It can be seen that the maximal evolution is actually slower than  at redshifts
at redshifts  Galaxies are growing so slowly at low redshifts that it is not possible to create a strong evolution in the
Galaxies are growing so slowly at low redshifts that it is not possible to create a strong evolution in the  ratio in a given galaxy, even if their black holes are not growing at all. This may well be why there is no evidence in Figure 11 for the "expected" increase in the observed
ratio in a given galaxy, even if their black holes are not growing at all. This may well be why there is no evidence in Figure 11 for the "expected" increase in the observed  The maximal change in
The maximal change in  over this redshift range would have been gentle enough that it would be very hard to observe. For this reason, we emphasize that our statements elsewhere in the paper concerning the evolution in
over this redshift range would have been gentle enough that it would be very hard to observe. For this reason, we emphasize that our statements elsewhere in the paper concerning the evolution in  should best be interpreted as implying a change of a factor of about 10 to
should best be interpreted as implying a change of a factor of about 10 to  rather than a precise particular dependence on redshift.
rather than a precise particular dependence on redshift.
Figure 13. Comparison of the maximal evolution of the  relation in a star-forming galaxy that stays on the Main Sequence, with our assumed
relation in a star-forming galaxy that stays on the Main Sequence, with our assumed  At low redshift, galaxies are growing so slowly in the stellar mass that strong evolution in the
At low redshift, galaxies are growing so slowly in the stellar mass that strong evolution in the  ratio is not possible, even if the black hole does not grow at all.
ratio is not possible, even if the black hole does not grow at all.
Download figure:
Standard image High-resolution image7.3. Downsizing
A number of authors (e.g., Barger et al. 2005; Hasinger et al. 2005; Labita et al. 2009; Li et al. 2011) have noted or discussed a "downsizing" of the quasar population. Although different authors often use this term to mean different things, it is most often used to denote the observational fact that lower-luminosity AGNs peak in comoving density at lower redshifts then higher-luminosity AGNs.
It is worth stressing that this may not have much physical significance. We have shown that it is possible to reproduce the strong observed redshift evolution in the QLF with a model based on the observed mass function of SF galaxies coupled with a mass-independent (but redshift-dependent) Eddington ratio distribution  This is shown more explicitly in Figure 14 where we show the comoving number density of quasars of different luminosity in the QLF, which is reproduced by our model. This emphasizes that the apparent downsizing signature in the AGN population can appear even though the distribution of Eddington ratios (and thus of specific black hole growth rates) is strictly independent of black hole mass at all redshifts in our model.
This is shown more explicitly in Figure 14 where we show the comoving number density of quasars of different luminosity in the QLF, which is reproduced by our model. This emphasizes that the apparent downsizing signature in the AGN population can appear even though the distribution of Eddington ratios (and thus of specific black hole growth rates) is strictly independent of black hole mass at all redshifts in our model.
Figure 14. Redshift evolution of comoving density of quasars for several different luminosities. The density of the lower-luminosity AGNs peaks at lower redshift then for high-luminosity AGNs. This behavior is naturally produced in our model even though the distribution of Eddington ratios is completely independent of black hole mass.
Download figure:
Standard image High-resolution imageFigure 15. Functional dependence of the factors  and
and  The black line corresponds to the "triangle" distribution given with Equation (6). The orange line is showing the result for the distribution shown in Equation (36) (with
The black line corresponds to the "triangle" distribution given with Equation (6). The orange line is showing the result for the distribution shown in Equation (36) (with  ), the red line is showing the result for the broken power-law distribution, given in Equation (9) (with
), the red line is showing the result for the broken power-law distribution, given in Equation (9) (with  ), while the brown line corresponds to the previous case, but with added scatter when converting from the star-forming galaxy mass function to the mass function of black holes in star-forming galaxies.
), while the brown line corresponds to the previous case, but with added scatter when converting from the star-forming galaxy mass function to the mass function of black holes in star-forming galaxies.
Download figure:
Standard image High-resolution imageFigure 16. QLF in the shape of a broken power-law distribution is show in blue, while in red we show results of convolution of the Schechter mass function and simple "triangle" distribution of the Eddington ratio (Equation (30)), with parameters set to the reproduce blue line. As we see, the agreement is excellent.
Download figure:
Standard image High-resolution imageFigure 17. Left:  redshift evolution. As in Figure 5, contours are showing 1-σ allowed regions of parameter space for fit, which was made with data at each individual redshift, while filled circles are the result of the global fit. Right:
redshift evolution. As in Figure 5, contours are showing 1-σ allowed regions of parameter space for fit, which was made with data at each individual redshift, while filled circles are the result of the global fit. Right:  evolution derived from
evolution derived from  evolution with our knowledge of redshift evolution of M∗ and with assumed mass scaling
evolution with our knowledge of redshift evolution of M∗ and with assumed mass scaling  All of the points and contours seem to align along a single line, suggesting an intimate link between these two quantities.
All of the points and contours seem to align along a single line, suggesting an intimate link between these two quantities.
Download figure:
Standard image High-resolution imageIt is clear that the apparent "downsizing" in our model arises as a natural consequence of two competing effects that are independent of mass. The first is the redshift evolution of the L∗, which shifts the luminosity function uniformly in luminosity, but which therefore produces a differential change in number density with luminosity. This shift is produced by the degenerate combination of evolution of the  mass ratio and characteristic Eddington ratio,
mass ratio and characteristic Eddington ratio,  The second is the redshift evolution of
The second is the redshift evolution of  that changes the number densities uniformly with luminosity. We have argued in this work that the evolution of
that changes the number densities uniformly with luminosity. We have argued in this work that the evolution of  is a direct consequence of the evolution of
is a direct consequence of the evolution of  coupled with a constant duty cycle. The combination of these two produces variation in the number density (at fixed luminosity) that changes with luminosity, producing a variation in the redshift of the peak in the number density as well as different rates of evolution at different luminosities.
coupled with a constant duty cycle. The combination of these two produces variation in the number density (at fixed luminosity) that changes with luminosity, producing a variation in the redshift of the peak in the number density as well as different rates of evolution at different luminosities.
7.4. Coherent Evolution of  and
and 
One of the most striking results of this paper is that the observed evolution of  of the QLF tracks the observed evolution of
of the QLF tracks the observed evolution of  of the SF galaxy mass function. This in turn implies that the
of the SF galaxy mass function. This in turn implies that the  knee of the Eddington ratio distribution
knee of the Eddington ratio distribution  has a more or less constant value, even though the change of the characteristic
has a more or less constant value, even though the change of the characteristic  "knee" is dramatic. We have argued that
"knee" is dramatic. We have argued that  is a good measure of a generalized "duty cycle" of quasars. Indeed, if the luminosity of individual quasars decays with a timescale τ then (Equation (10))
is a good measure of a generalized "duty cycle" of quasars. Indeed, if the luminosity of individual quasars decays with a timescale τ then (Equation (10))  will be direct measure of the birthrate of quasars in SF galaxies.
will be direct measure of the birthrate of quasars in SF galaxies.
By applying simple continuity equations to the observed evolution of the SF galaxy mass function, Peng et al. (2010) derived an expression for the rate of the mass-quenching process,  , which may be written
, which may be written

where sSFR(z) is the redshift-dependent specific star formation rate of the SF Main Sequence. It has been well established that sSFR was much higher in the past and a useful representation is (Lilly et al. 2013 and references therein)

AGN activity in "quasar-mode" is one of the many processes that have been proposed (e.g., Granato et al. 2004; Hopkins et al. 2008a; King 2010) to drive the mass-quenching of galaxies. If a single quasar event is responsible for quenching, then this would require  (from Equation (10)) to be equal to
(from Equation (10)) to be equal to  These can only be equated for our inferred constant
These can only be equated for our inferred constant  for a particular redshift and mass dependence of the decay time τ.
for a particular redshift and mass dependence of the decay time τ.

We would require quasars to fade faster at high redshift and at high galaxy masses. We could well imagine ways in which this would occur, e.g., because of the shorter dynamical timescales of galaxies at high redshift.
However, the above picture is probably oversimplistic. We could well expect the physics of quenching to be more complex. It is quite plausible that the energy source for quenching is AGN activity but that the effectiveness of this energy injection depends on the stellar or halo mass of the system (the Peng et al. 2010 quenching law can be written in terms of a redshift-independent survival probability that depends only on mass). This would then break the simple link between  and
and 
8. SUMMARY AND CONCLUSIONS
We have presented a simple, phenomenological model that aims to link the evolving galaxy population with the evolving AGN population. We use our observational knowledge of the evolving galaxy mass function and of the evolving QLF to connect these two populations and to create a global model to interpret the AGN population, including biases associated with sample selection.
Our model is based on three observationally motivated Ansätze, namely that
- 1.radiatively efficient AGNs are found in SF galaxies,
- 2.the probability distribution of the Eddington ratio does not depend on the black hole mass of the system, and
- 3.the mass of the central black hole is linked to the stellar mass.
The QLF is then a straightforward convolution of the black hole mass function with the distribution of Eddington ratios  while the former is itself a convolution of the galaxy mass-function with the
while the former is itself a convolution of the galaxy mass-function with the  relation. These heuristic assumptions ensure that our model is simple enough to be analytically tractable, while still capturing the main characteristics of the galaxy and AGN population.
relation. These heuristic assumptions ensure that our model is simple enough to be analytically tractable, while still capturing the main characteristics of the galaxy and AGN population.
The main conclusions of this model analysis can be summarized as follows:
- 1.The "broken" or "double" power law form of the QLF is a consequence of the underlying Schechter mass function and a "double" power-law, mass-independent, Eddington ratio distribution. We show how the parameters of the QLF are straightforwardly connected with the input functions. Most importantly, the knee of the QLF,
 is proportional to the product of the M∗ of the galaxy mass function, the ratio
is proportional to the product of the M∗ of the galaxy mass function, the ratio  and the position
and the position  of the break in the Eddington ratio distribution while the
of the break in the Eddington ratio distribution while the  normalization of the QLF is proportional to the product of the
normalization of the QLF is proportional to the product of the  normalization of the SF galaxy mass function and the
normalization of the SF galaxy mass function and the  normalization of the Eddington ratio distribution, which can be loosely interpreted as a "duty cycle." Our simple convolution model makes clear and testable predictions for the distribution of host galaxy masses (relative to the SF galaxy Schechter M∗) for different AGN luminosities (relative to L∗). At high luminosities (above the AGN L∗) this is a Schechter function with the SF M∗ but a faint end slope given by
normalization of the Eddington ratio distribution, which can be loosely interpreted as a "duty cycle." Our simple convolution model makes clear and testable predictions for the distribution of host galaxy masses (relative to the SF galaxy Schechter M∗) for different AGN luminosities (relative to L∗). At high luminosities (above the AGN L∗) this is a Schechter function with the SF M∗ but a faint end slope given by 
- 2.There is a remarkable consistency in the redshift evolution of
 normalization of SF mass function and the
normalization of SF mass function and the  normalization of the QLF. These two characteristic densities track each other closely out to redshifts of
normalization of the QLF. These two characteristic densities track each other closely out to redshifts of  and possibly to even higher redshifts. This implies that the generalized "duty cycle" of AGNs is surprisingly constant with redshift.
and possibly to even higher redshifts. This implies that the generalized "duty cycle" of AGNs is surprisingly constant with redshift. - 3.In contrast, the QLF L∗ evolves strongly with redshift, with evolution being at least
 up to
up to  Given that there is strong evidence for no change in the galaxy M∗ over this redshift range, this evolution in L∗ is driven by an evolution in the characteristic "knee" in the Eddington ratio distribution
Given that there is strong evidence for no change in the galaxy M∗ over this redshift range, this evolution in L∗ is driven by an evolution in the characteristic "knee" in the Eddington ratio distribution  or in the mass scaling between stellar mass and black hole mass,
or in the mass scaling between stellar mass and black hole mass,  or some combination of the two. The QLF evolution is degenerate in changes of these two quantities.
or some combination of the two. The QLF evolution is degenerate in changes of these two quantities.
We then explore this degeneracy by comparing predictions of our model, incorporating the relevant selection cuts, for the distribution of systems in the SDSS AGN mass–luminosity plane(s) using black hole mass estimates for individual AGN. We find a good match with an evolving  in SF systems. This implies that the observed
in SF systems. This implies that the observed  increase in
increase in  back to
back to  would be due to an equal split between a
would be due to an equal split between a  change in
change in  and a
and a  change in characteristic Eddington ratio
change in characteristic Eddington ratio  .
.
We show that this is compatible with the observed  relations in both quenched and in SF galaxies in the local universe, both in terms of the mean relations and the scatter.
relations in both quenched and in SF galaxies in the local universe, both in terms of the mean relations and the scatter.
We also make the important point that much weaker evolution, more like  would be deduced by observers, after correcting for the "Lauer bias," if (as they usually of necessity do) they compare black hole masses in active (SF) systems at high redshift (
would be deduced by observers, after correcting for the "Lauer bias," if (as they usually of necessity do) they compare black hole masses in active (SF) systems at high redshift ( ) with those in quiescent systems at low redshift. Similarly, much weaker evolution would also be seen if black hole masses were to be compared solely within the passive population at different redshifts.
) with those in quiescent systems at low redshift. Similarly, much weaker evolution would also be seen if black hole masses were to be compared solely within the passive population at different redshifts.
The inferred  evolution in SF systems is likely simplistic, and unlikely to hold all the way down to the lowest redshifts simply because there is not enough star formation to change m* fast enough, even if black holes are not growing at all. Our use of a
evolution in SF systems is likely simplistic, and unlikely to hold all the way down to the lowest redshifts simply because there is not enough star formation to change m* fast enough, even if black holes are not growing at all. Our use of a  evolutionary model should be interpreted more loosely as a way of getting a factor of 2.5 change between
evolutionary model should be interpreted more loosely as a way of getting a factor of 2.5 change between  in active systems at
in active systems at  when compared with the same relation in passive systems today, rather than as a precise relation that absolutely holds at all redshifts.
when compared with the same relation in passive systems today, rather than as a precise relation that absolutely holds at all redshifts.
However, we make the interesting point that an evolution of the form  would, when coupled with the observed changes in the sizes of galaxies, which typically scale as roughly
would, when coupled with the observed changes in the sizes of galaxies, which typically scale as roughly  have the feature of producing an
have the feature of producing an  relation that would be more or less independent of redshift. This could then explain why the present-day
relation that would be more or less independent of redshift. This could then explain why the present-day  relation would have lower scatter than the
relation would have lower scatter than the  relation, even if σ plays no direct role in black hole growth. Alternatively, a fundamental redshift-independent
relation, even if σ plays no direct role in black hole growth. Alternatively, a fundamental redshift-independent  relation could be the physical origin of an apparent
relation could be the physical origin of an apparent  evolution.
evolution.
We stress that the most basic features of the model do not depend on the redshift dependence of  which is driven largely by the possibly uncertain observational estimates of black hole masses in high-redshift AGNs.
which is driven largely by the possibly uncertain observational estimates of black hole masses in high-redshift AGNs.
Not least, quite independent of the form of any evolution in  the generic model naturally reproduces the counterintuitive "sub-Eddington boundary" in the (
the generic model naturally reproduces the counterintuitive "sub-Eddington boundary" in the ( ) plane that has been noted by Steinhardt & Elvis (2010b) without the need to invoke any new physical effects. The generic model also produces the apparent "downsizing" of the AGN population (e.g., Hasinger et al. 2005). We stress that both of these apparently mass-dependent effects are achieved in the model with an Eddington ratio distribution that is completelyindependent of black hole mass at all redshifts.
) plane that has been noted by Steinhardt & Elvis (2010b) without the need to invoke any new physical effects. The generic model also produces the apparent "downsizing" of the AGN population (e.g., Hasinger et al. 2005). We stress that both of these apparently mass-dependent effects are achieved in the model with an Eddington ratio distribution that is completelyindependent of black hole mass at all redshifts.
We thank Simon Birrer for providing us with the full output of the model presented in Birrer et al. (2014). We also thank Peter Behroozi for providing us with the galaxy mass functions that were used as the input in Behroozi et al. (2013b). Sebastian Seehars has helped in creating fitting procedures. In developing this work, we have benefited from stimulating discussions with Charles Steinhardt, Andreas Schulze, Kevin Schawinski, and David Rosario. We are also very grateful for the very perceptive comments provided by the anonymous referee. This work has been supported by the Swiss National Science Foundation.
APPENDIX A:
Here we will show analytically how the convolution of a Schechter mass function  with a triangular Eddington ratio distribution
with a triangular Eddington ratio distribution  in Equation (6) gives rise to a double power-law QLF and the simple relations between parameters given in (12). In this simplest case when
in Equation (6) gives rise to a double power-law QLF and the simple relations between parameters given in (12). In this simplest case when  below
below  combining Equations (3), (6), and (16) leads to
combining Equations (3), (6), and (16) leads to

where ![${\rm{\Gamma }}[x]$](https://content.cld.iop.org/journals/0004-637X/811/2/148/revision1/apj519757ieqn327.gif) is the Euler gamma function, given by
is the Euler gamma function, given by ![${\rm{\Gamma }}[x]={\displaystyle \int }_{0}^{\infty }{t}^{x-1}{e}^{-t}{dt}$](https://content.cld.iop.org/journals/0004-637X/811/2/148/revision1/apj519757ieqn328.gif) , and
, and ![${\rm{\Gamma }}[x,y]$](https://content.cld.iop.org/journals/0004-637X/811/2/148/revision1/apj519757ieqn329.gif) is incomplete gamma function, defined as
is incomplete gamma function, defined as ![${\rm{\Gamma }}[x,y]={\displaystyle \int }_{y}^{\infty }{t}^{x-1}{e}^{-t}{dt}.$](https://content.cld.iop.org/journals/0004-637X/811/2/148/revision1/apj519757ieqn330.gif) On the other hand, we know that the integral of distribution of Eddington ratios has to be equal to fd
On the other hand, we know that the integral of distribution of Eddington ratios has to be equal to fd

which gives

Combining Equations (27) and (29), we arrive at an expression for the QLF,

where we separate the "normalization" from the rest of the expression in curly brackets. We can expand this expression at low and high L to show asymptotic power-law behavior. Expanding around L = 0 gives

so we see that the dominant term will be  and that
and that  This is a special case of our formula
This is a special case of our formula  , as in this case
, as in this case  is effectively minus infinity. Expanding around
is effectively minus infinity. Expanding around 

we see that dominant term is  giving rise to the equation
giving rise to the equation 
Defining the double power law as in Equation (1), we find the expression for L∗ and  is given by
is given by

As would be expected the L∗ and  are related to the input
are related to the input  and
and  via the characteristic
via the characteristic  and the normalization of
and the normalization of  given by fd.
given by fd.
We have numerically fitted the resulting  around L∗ with the broken power law given in Equation (1) (with
around L∗ with the broken power law given in Equation (1) (with  ) for various
) for various  values and plot the resulting offsets
values and plot the resulting offsets  and
and  in Figure 15 such that
in Figure 15 such that

It can be seen that, as would be expected from Equation (30), the values of  and
and  vary with
vary with  The standard double power-law Equation (1) is a surprisingly good representation of the analytic result in Equation (30). The example of the power-law shape and the result from our convolution are shown in Figure 16.
The standard double power-law Equation (1) is a surprisingly good representation of the analytic result in Equation (30). The example of the power-law shape and the result from our convolution are shown in Figure 16.
We can also repeat this exercise with a second form of  that is flat below
that is flat below  i.e., has
i.e., has  replacing fd by
replacing fd by  i.e.,
i.e.,

where we incorporate the fact that Δ factors depend on the assumed shape of the Eddington ratio. This can again be seen in Figure 15, where we also show results of fitting with the Eddington ratio distribution, which has a sharp break at  i.e.,
i.e.,

APPENDIX B:
In this section we wish to point out one interesting and suggestive fact that arises from fits that were discussed in Section 5. We show on the left-hand side of Figure 17 the relation obtained between L∗ and the bright end slope of the QLF,  There is a clear increase in the bright end slope
There is a clear increase in the bright end slope  as L∗ increases with redshift. At
as L∗ increases with redshift. At  as
as  stalls and then declines, we also see
stalls and then declines, we also see  decreasing again, although not in unison with L∗ in the sense that the track in the (
decreasing again, although not in unison with L∗ in the sense that the track in the ( ) plane is displaced. We can plot an equivalent diagram in the (
) plane is displaced. We can plot an equivalent diagram in the ( ) plane by converting
) plane by converting  to
to  using an
using an  ratio and Equation (13) and setting
ratio and Equation (13) and setting  (Equation (4)). The steepening of
(Equation (4)). The steepening of  as
as  increases might qualitatively be expected if there were some maximum value of the Eddington ratio
increases might qualitatively be expected if there were some maximum value of the Eddington ratio  As
As  increased toward such a limit, then
increased toward such a limit, then  above
above  would have to steepen, so as to get down to zero at the limiting
would have to steepen, so as to get down to zero at the limiting 
An interesting question is then whether we can find an evolving (i.e., redshift-dependent)  ratio that will cause the "up" and "down" tracks in Figure 17 to lie on top of each other. We find that introducing
ratio that will cause the "up" and "down" tracks in Figure 17 to lie on top of each other. We find that introducing  produces a good congruence in the (
produces a good congruence in the ( ) tracks associated with the rise and decline of
) tracks associated with the rise and decline of  This is shown in the right-hand panel, where we show the (
This is shown in the right-hand panel, where we show the ( ) tracks obtained by using
) tracks obtained by using  The congruence with this particular
The congruence with this particular  evolution is suggestive but cannot be taken as a strong indication of this particular evolution of
evolution is suggestive but cannot be taken as a strong indication of this particular evolution of 
However, the values of  that are implied (in our convolution model) at high redshifts by the high L∗ are getting uncomfortably high, unless there is a strong increase in
that are implied (in our convolution model) at high redshifts by the high L∗ are getting uncomfortably high, unless there is a strong increase in  relative to the canonical zero redshift value of
relative to the canonical zero redshift value of  as can be seen on the right-hand plot of Figure 17. With
as can be seen on the right-hand plot of Figure 17. With  evolution,
evolution,  is implied to be −0.8 dex at
is implied to be −0.8 dex at  but without this evolution,
but without this evolution,  is implied to be +0.15 dex, i.e., above the Eddington limit! This would mean that the characteristic Eddington ratio at this redshift would be above the Eddington limit, with many of the objects being super-Eddington. Both observations and theoretical work suggest that the fraction of AGNs that crosses this limit is small (e.g., Woo & Urry 2002; Netzer & Trakhtenbrot 2007; Hopkins & Quataert 2010; Shen et al. 2011; Trakhtenbrot & Netzer 2012).
is implied to be +0.15 dex, i.e., above the Eddington limit! This would mean that the characteristic Eddington ratio at this redshift would be above the Eddington limit, with many of the objects being super-Eddington. Both observations and theoretical work suggest that the fraction of AGNs that crosses this limit is small (e.g., Woo & Urry 2002; Netzer & Trakhtenbrot 2007; Hopkins & Quataert 2010; Shen et al. 2011; Trakhtenbrot & Netzer 2012).










































