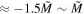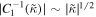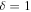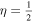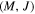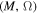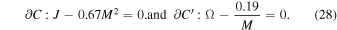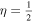Abstract
For a Kerr black hole (KBH) with spin J and mass M in a steady electromagnetic field, a special Wald vacuum solution (WVS) has been found in the case of the no-source uniform field. For WVS, the Meissner effect (ME) occurs only in the the extreme KBH, where M2/J = 1, in this case, the magnetic field is totally excluded from the event horizon (EH) of KBH. However, WVS does not consider the Hawking radiation (HR) but treats KBH as an absolutely black body. If HR is added , researchers believe that the condition is not so restricted and it is possible for ME to occur in the less-extreme case. How less is the "less-extreme case"? This paper tries to answer this question. Since the Hawking temperature TH of KBH defined by HR is proportional to the surface gravity κ at the EH, this question is actually about the so-called existence/non-existence of ME (ME/NME) or superconducting phase transition. In this paper, we study the connection between the superconductivity of KBH-EH and the existence of Weyl fermion. Using thermodynamic formulas and the KBH state equation, we prove that the inherent-parameter condition for ME to occur is in force-free fields whether it be in the simple axisymmetric vacuum zero source case or in the non-zero source case, which can be described by the nonlinear Grad–Shafranov equation. We suggest that this is a second-order phase transition and calculate the critical exponents δ = 1 and η = 1/2 for the specific heat diverging at constant J.
1. Introduction
Black hole thermodynamics has been an intriguing subject of discussion for decades. The analogy between space–time with black hole horizon and thermodynamics have been extensively investigated (Bardeen et al. 1973). The four laws of black hole thermodynamics were discovered by Carter, Hawking, and Bardeen (Bardeen et al. 1973). These laws are physical properties that black holes are believed to satisfy. A black hole behaves as a black body with the Hawking temperature , where κ, c, kB, and denote the surface gravity of the event horizon (EH), light velocity, Boltzmann constant, and Planck constant respectively (Carr & Hawking 1974; Hawking 1975). Since thermodynamic quantities correspond to microscopic structures, some researchers have attempted to explain black hole properties through exploring phase transition of the small-large charged Schwarzschild black hole (SBH/LBH; Hawking & Page 1983; Chamblin et al. 1999a, 1999b; Wei & Liu 2015). This kind of phase transition is similar to the liquid–gas transitions, which are first-order (Liu et al. 2014). Compared with the Schwarzschild black hole, there might exist more complex phenomena in the Kerr black hole (KBH) since it has additional spin J.
Blandford & Znajek (1977) gave the nonlinear Grad–Shafranov (G–S) equation for a force-free magnetosphere (FFM) of the curved Kerr space–time, which can describe the energy extraction process (Blandford & Znajek 1977). In this progress, KBH can be heated or cooled to reach a phase transition. One recalls Boltzmanns insight: "If you can heat it, it has microscopic structure." The rotational energy of the KBH can be converted into the thermal and kinetic energy of the surrounding plasma. The electron would emit many photons, which in turn can produce a plentiful supply of the electron–positron pairs. When a KBH is immersed in a steady electromagnetic field, for the Wald vacuum solution (WVS; Wald 1974), King et al. (1975) found that all magnetic fields are expelled out of the EH of the extremal KBH (King et al. 1975). The WVS is time-independent and it describes a KBH being immersed in a uniform magnetic field aligned with the black hole spin axis. Bičák & Dvořák (1976) and Bičák & Janis (1985) generalized this result (Bičák & Dvořák 1976; Bičák & Janis 1985). They showed that if the black hole is extremal (namely M/a = 1, where M denotes the mass of KBH and a = J/M), the non-monopole component of the magnetic flux could not penetrate the EH for all steady axisymmetric vacuum solutions. The interesting phenomenon is called Meissner effect (ME), which is the expulsion of magnetic field lines out of the EH and the quenching of jet power for the KBH (Bičák & Janis 1985; Penna 2014). However, WVS does not consider the Hawking radiation (HR) but treats KBH as an absolute black body (Carr & Hawking 1974; Wald 1974). If the HR is considered, researchers believe that the condition is not so restricted and it is possible for ME to occur in less-extreme case (Penna 2014). Some observations about astrophysical black holes with high spins would support this argument (McClintock et al. 2006; Gou et al. 2011; McClintock et al. 2014). The spin parameters of the near-extreme KBHs in Cyg X-1 and GRS 1915+105 have been measured to be M2/J greater than 1. Jets from these black holes could be quenched by the ME.
Recently, for zero or non-zero sources, the ME in the steady axisymmetric FFM attracts lots of attention, where HRs have been considered. Many physicists want to know whether the Blandford–Znajek (BZ) process would be quenched if the ME exists in the real astrophysical environment. However, this effect was never seen in the previous general relativistic magnetohydrodynamic simulations. In our previous work (Gong et al. 2016), we discuss the external-field condition for ME to occur, which is on the external EH. Here Ω0 is the angular velocity of KBH-EH, Hϕ corresponds to twice the poloidal electric current, and , which satisfies , with Ai and being the ith component of vector potential and the radius of external EH (Blandford & Znajek 1977; Znajek 1977), we denote as X,y. Besides, Znajek (1978) suggested that the effective electric resistance of the KBH-EH surface is a non-zero constant indicated by G–S equation if the BZ mechanism works (Blandford & Znajek 1977; Znajek 1978). In Gong et al. (2016), we prove that the BZ mechanism only works when the angular velocity ω of the field is strictly slower than the angular velocity Ω0 of KBH. If the BZ mechanism does not work, the resistance may vanish. It could be regarded as a superconducting phase transition since the electric resistance suddenly vanishes. At the EH, there does not exist any magnetic field, this means ME will occur. Furthermore, the resistance could be vanishing at the EH. These facts mean that the EH has superconductivity. In condensed matter physics (CMP) research, due to flux quantization, the ME is closely related to zero-resistance phenomena. Generally speaking, when ME occurs, the superconductivity happens.
In this paper, we study the connection between the superconductivity of KBH-EH and the existence of Weyl fermion (WF). We also give the thermodynamic KBH state equation and the inherent-parameter condition for the existence/non-existence of the ME (ME/NME) phase transition, where . The divergence of the specific heat at constant J tells us that this is a second-order phase transition. Therefore, we also calculate the critical exponents and find the critical points, further we draw the phase diagrams in (M, J) and (M, Ω) coordinates. Moreover, we provide a possible explanation that the parameters of ME phase exactly correspond to the positive specific heat condition. It is a necessary condition to reach holographic superconductivity (Papantonopoulos 2011).
For simplicity, the constant , kB, c, and the gravitational constant G equals a unit of 1.
2. Meissner Effect
The Kerr metric in Boyer–Lindquist coordinates is
Here , , , , and .
For solving the problem about a KBH with spin J and mass M in a steady electromagnetic field, one needs to know some information about the electromagnetic field, such as the electromagnetic tensor Fμν or the vector potential Aν. A special WVS has been extensively researched.
2.1. Wald Vacuum Solution
In the WVS, the field reads (Wald 1974)
where the square bracket denotes antisymmetrization of the indices, and . The Carter orthonormal vector fields are in Boyer–Lindquist components as follows,
The electromagnetic field in the Carter frames reads
Based on these following relations
one can get
In the extreme KBH, where a = M, it is easy to know that at the EH, . In other words, there does not exist any electromagnetic field at the EH for the extreme KBHs.
2.2. BZ Mechanism
Wald finished his work before the pioneering literature about HR was published (Carr & Hawking 1974; Wald 1974). So WVS does not consider the HR but treats KBH as an absolutely black body. Where the particle number is small enough, WVS is a good approximation. Later, a more general nonlinear equation, called the G–S equation, was discovered (Blandford & Znajek 1977). It is primarily used to analyze the energy extraction process of a force-free magnetosphere in the curved Kerr space–time. In the G–S equation, the field induced by HR particles can be added, which makes it very hard to solve.
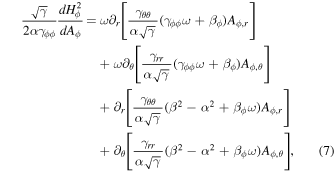
The constraint differential equation for the FFM around KBHs is given by Menon & Dermer (2005) as
where , , , , , , . The angular velocity is a function of Aϕ. Considering the Euler–Lagrange equation, which is , the Lagrangian for Equation (7) can be expressed as (Gong et al. 2016)
One can get the external and inner light surfaces for the given ω by solving
Namely , where , . Let , and we assume that is a function of . Then Equation (7) becomes G–S equation,which reads
Here, i = r or μ, , and .
In Gong et al. (2016), for the G–S equation in the case where and , we prove that the ME expels magnetic fields out of the external EH and it also expels magnetic fields out of the inner light surface. The magnetic fields outside the inner light surface could not go to the region between the external EH and the inner light surface. For a stationary, axisymmetric, force-free and magnetically dominated field, its configuration cannot possess a closed loop of poloidal field line (Gralla & Jacobson 2014). Thus the inner light surface must meet the EH when ME occurs. In other words, the angular velocity ω must equal Ω0 at the EH. If the inner light surface does not meet the EH, ME would expel magnetic fields out of the external EH and the inner light surface. Since the inner light surface, which is defined by L = 0, must be located outside the external EH, the configuration of magnetic field between the external EH and the inner light surface will possess a closed loop of poloidal field line. It will contradict to the result of Gralla & Jacobson (2014).
The Lorentz invariant to the Carter observers is , where the Carter field components given by Znajek (1977) are
Then we can get , where is the velocity of a observer rotating around the KBH with angular velocity ω with respect to the Carter observers (). The final result of the Lorentz invariant is
Then we can get the current density (; denotes the covariant derivative). Specially, for the vacuum case, which means jμ ≡ 0, the electromagnetic field vanishes at the EH if ME occurs. There is no charged particle produced by HR.
For the G–S equation, one can get the electric current density in the coordinates from Equation (11), which reads (Blandford & Znajek 1977)
Here, g is the determinant of the metric tensor gμν. When ω = Ω0, the boundary condition at the EH leads to Hϕ = 0.
The angular velocity ω is a function of Aϕ and ω = Ω0 at the EH, then , Δ = 0 and L = 0 at the EH. Since is continuous, if we further assume it is bounded (namely, ), we can deduce that so that . Here means that infinitesimal varibles x and y have the same order. From Equation (13), one can know that the electromagnetic field vanishes at the EH. Based on Equation (13), we get
where . Moreover, at the EH,
Besides, due to the fact that the current density is a physical observable that cannot move faster than light, is not a space-like vector (e.g., ). In order to satisfy , and need to be 0 at the EH. From Equation (13), one can know that jr = 0 at the EH when the ME occurs. The charged particles produced by HR cannot drop into the KBH. We think the charged particle with light velocity can stay on the EH. If the current density is a null-vector (namely ) and , the current carrier is a charged particle with light velocity, whose mass should be nought. When the interaction between them is very weak, the resistance should be vanishing (Punsly 2008). The most possible candidate serving as the carrier is the mysterious WF, which is massless and permitted to carry charges. If the carrier is an ordinary charged particle with mass, the null-vector must satisfy . In other words, the electric current at the external EH vanishes. Thus, in theory, we can test the existence of WF by measuring if there is a nonvanshing current on the EH surface when ω = Ω0. Moreover, because the resistance of particles with mass hardly vanishes (Punsly 2008), these charge carriers should be massless. Then, WF is a more possible candiate than some so-called supersymmetric particles. It should be pointed out that the above arguments are not explicitly based on the quantum effect. However, since the thermal behaviors of the black hole are essentially quantum mechanical, so are its electric behaviors. The quantum fluctuations might change this result, the thorough answer to this problem may require a better self-consistent theory of quantum gravity (Natsuume 2015).
3. Phase Transition
For KBH, the external and inner EH exists at . Furthermore, we notice that the surface gravity κ of KBH reads . Thus we have the equation of the mass function satisfying
At constant J, when M = J, κ = 0; when , κ = 0. Thus, for the same surface gravity κ, there exists a different mass M. Meanwhile, we have the first law of KBH thermodynamics in the electromagnetic field, which is , with the external surface area of EH. Here dW is the rotation energy extracted by the field. Punsly (2008) has shown that axisymmetic vacuum fields could not extract energy from a black hole (Punsly & Coroniti 1989; Punsly 2008), namely dW = 0. For the G–S equation, , the effective power of electromagnetic field affecting KBH satisfies (Blandford & Znajek 1977)
When ω = Ω, . Therefore, we have the first law of KBH thermodynamics that reads
Here, M, , J, and A+ is analogous to the internal energy, pressure, volume, and entropy of gas (Ho et al. 1997). The field does not affect the state of KBH, so we have Therefore, In the thermodynamic state equation, satisfies
Let , , we have the variable  satisfying
satisfying
The specific heat at constant spin J is
Differentiating Equation (20) with respect to κ, we have Apart from the trivial diverging points (κ = 0 and ), the singular points of CJ correspond to the roots of the function f( ) which can be written as
) which can be written as
The reciprocal of specific heat satisfies
As shown in Figure 1, the zero point is  c ≈ 1.5 by numerical calculation.
c ≈ 1.5 by numerical calculation.
Figure 1. Curve f( ), with
), with  = M2/J, which determines the critical value
= M2/J, which determines the critical value  c ≈ 1.5, where specific heat diverges.
c ≈ 1.5, where specific heat diverges.
Download figure:
Standard image High-resolution imageSubstituting into Equation (19), . The critical point at constant J satisfies
The critical surface gravity κc reads
The critical exponent δ and η is defined by
Here, the reduced surface gravity and mass satisfies , . Then we let J = 1, so  = M2, Mc = 1.224, and κc = 0.174. From Equation (23), the reciprocal of specific heat C1 satisfies
= M2, Mc = 1.224, and κc = 0.174. From Equation (23), the reciprocal of specific heat C1 satisfies
When , near critical point Mc, we can re-write it as . Meanwhile, we have . So, near point κc. Therefore, the exponent and .
As shown in Figure 2, in the ME/NME phase diagram, the critical curve in coordinates and the corresponding curve in coordinates reads
Figure 2. Left panel: (a) phase diagram in (M, J) coordinates; right panel: (b) phase diagram in (M, Ω) coordinates. NP represents the non-physical zone.
Download figure:
Standard image High-resolution imageWhen the Equation (28) is established, the spectific heat is unbounded. It means this is a second-order phase transition, which is the same as the superconducting transition in CMP. A recent work suggests that due to the absence of an adequate free paremeter in black holes, all kinds of phase transitons and critical phenomena share the same critical exponents and scaling powers (Mandal et al. 2016). It is well-known that for an extreme KBH, the ME must occur. Furthermore, there are not any other critical points for the Kerr sequence. Based on the continuity of the phase zone, one could believe that in the region sandwiched by J ≤ M2 and J ≥ 0.67 M2, there exists the ME phase. Due to the nonlinearity and complexity, more elaborate theoretical proof and numerial calcuations need to be done.
One can notice that the parameters of the ME phase exactly correspond to the positive specific heat condition. It is a necessary condition to reach holographic superconductivity. In the superconductor, we need condensation of the matter field produced by HR. A non-zero condensate corresponds to a static non-zero field outside the black hole. This viewpoint is helpful to understand the physical cause of the phase transition. Furthermore, the near-horizon extreme KBH is an anti-de Sitter(AdS) space (Guica et al. 2009). AdS space is another necessary condition to reach holographic superconductivity. Besides, similar to AdS/CFT correspondence (Maldacena 1999), the extreme KBH has the Kerr/CFT correspondence (Guica et al. 2009). Here, conformal field theory is abbreviated as CFT. One may develop a kind of perturbation theory for the less-extreme KBH case. It is a possible way to resolve this problem. We will focus on the proof of superconductivity in our future work.
4. Summary and Discussion
We give the thermodynamic state equation of KBH, calculate the condition of the ME/NME phase transition, and draw the phase diagrams. We also get the critical exponents δ = 1 and . It must be pointed out that the ME/NME phase transition is only a terminology, like SBH/LBH phase transition. Lacking the knowledge about microscopic structure of KBH, it is hard to tell whether ME is the essential criterion for the phase transition or not. Comparing with Bardeen–Cooper–Schrieffer superconductivity, there may exist a more natural phenomenon where the electric resistance vanishes. However, the phase transition suggests that there exists a kind of massless and charged particle, possibly WF, which waits to be confirmed in the future. If ME and zero-resistance occurs simultaneously when the BZ mechanism does not work, one can study if the critical magnetic field exists for the linear vacuum case or more complex cases. Since ME/NME phase transition is second order, one could find the order parameter and construct the corresponding Landau–Ginzburg equation. Besides, AdS KBH with negative cosmological constant Λ or Kerr–Newman black hole with charge Q may exhibit richer phase transitions. It is very difficult to find the condition for ME to occur in these cases. The present calculation for phase transition of KBH serves as the first step to explore the above mentioned problems, which will be studied in our future work. We are looking forward to understanding these phenomena in future research.
This work was supported in part by startup funding of the South University of Science and Technology of China, the Shenzhen Peacock Plan and Shenzhen Fundamental Research Foundation (grant No. JCYJ20150630145302225) and National Natural Science Foundation of China (grant No. 11681240276 and grant No. 11674152).



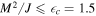

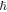
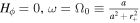
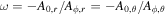
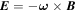
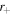

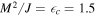
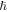
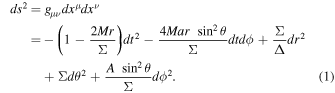
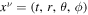
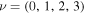
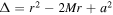
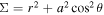

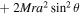
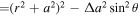
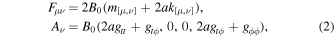
![$[\mu ,\nu ]$](https://content.cld.iop.org/journals/0004-637X/835/2/247/revision1/apjaa5720ieqn19.gif)


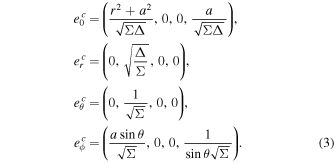

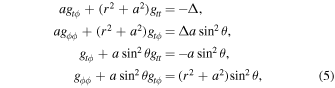
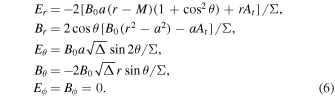

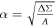
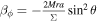
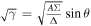
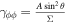
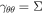
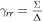
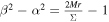
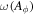
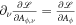
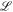
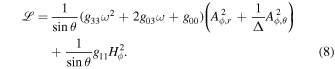
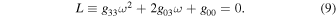
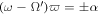
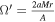
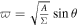
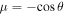
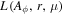
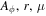
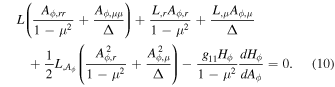
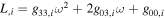

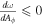



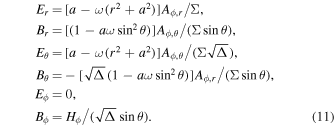

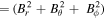

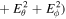
![$=\,[1-{({\nu }_{c}^{\phi })}^{2}][{B}_{r}^{2}+{B}_{\theta }^{2}]\,$](https://content.cld.iop.org/journals/0004-637X/835/2/247/revision1/apjaa5720ieqn49.gif)
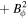
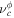
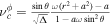

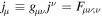
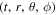
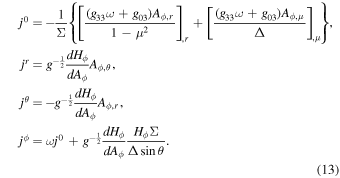
![${H}_{\phi }=\tfrac{\sin \theta [\omega ({r}_{+}^{2}+{a}^{2})-a]}{{r}_{+}^{2}+{a}^{2}{\cos }^{2}\theta }{A}_{\phi ,\theta }$](https://content.cld.iop.org/journals/0004-637X/835/2/247/revision1/apjaa5720ieqn55.gif)
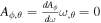
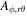
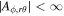
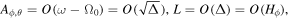
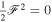
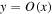
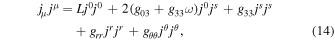
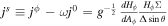
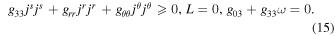

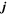
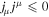
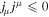
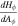
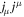
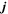
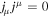
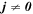
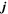

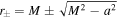
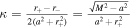
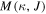
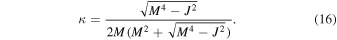
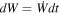
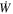
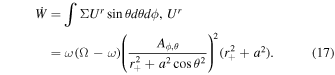
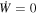
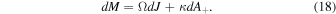
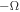
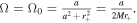
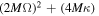
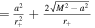
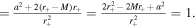
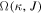
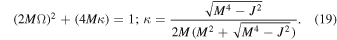
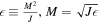
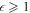
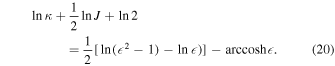
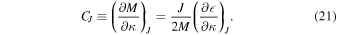
![${\left(\tfrac{\partial \epsilon }{\partial \kappa }\right)}_{J}^{-1}=\kappa \left[\left(\tfrac{\epsilon }{{\epsilon }^{2}-1}\right)-\left(\tfrac{1}{2\epsilon }+\tfrac{1}{\sqrt{{\epsilon }^{2}-1}}\right)\right].$](https://content.cld.iop.org/journals/0004-637X/835/2/247/revision1/apjaa5720ieqn91.gif)

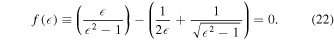
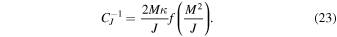


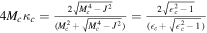

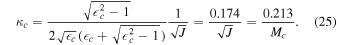
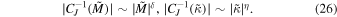
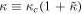
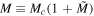
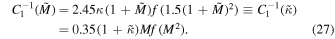

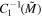
![$\approx \,0.7[1.2(1-5\tilde{M})-0.3(1-2\tilde{M})-0.9(1-3.6\tilde{M})]$](https://content.cld.iop.org/journals/0004-637X/835/2/247/revision1/apjaa5720ieqn102.gif)