A Spectral-line Analysis of the G8 III Standard ε VIR

Few stars have been recruited to the ranks of "standard star" more than ε Vir (HR 4932, HD 113226, HIP 63608, BD +11° 2529) and it seems to be eminently suited for the role, being stable and inactive and generally well-behaved. Although not included in the early definition of the MK system (Johnson & Morgan 1953), it was incorporated into the system in due course (Greenstein & Keenan 1958; Morgan & Keenan 1973) as a G8 IIIab standard star. Keenan felt that a good spectroscopist working with high-quality spectra could discern finer luminosity steps than the full Roman numerals. Thus, a star noticeably more luminous was to be classed as IIIa and less luminous as IIIb. The mid-range luminosity was termed IIIab. Indeed, with an apparent visual magnitude of 2.79 and a parallax of 29.76 ± 0.14 mas (from the SIMBAD data base, Wenger et al. 2000), the absolute magnitude is 0.16 ± 0.01. This places the star only ∼0.14 mag above the middle of the class III G8 giants in agreement with Keenan's selection. Because the star is now a standard in the MK classification framework, it should never be classed otherwise, unless working outside the MK system. ε Vir has also been selected as a Gaia benchmark standard (Heiter et al. 2015).

In addition to being a classification standard, ε Vir has been used repeatedly as a reference for chemical analyses. Although not the first to analyze ε Vir, Cayrel & Cayrel (1963) became a classic and the stepping stone for the chemical analysis of numerous other stars. Among these are Strom et al. (1971), Warren (1973), Williams (1973), Blanc-Vaziaga et al. (1973), Hearnshaw (1977), Whitford & Rich (1983), Cottrell & Sneden (1986), Arimoto & Cayrel de Strobel (1988), Jofré et al. (2014), and Bluhm et al. (2016). The metallicity, [Fe/H], measurements of ε Vir itself span a considerable range. For example, the 17 catalog values listed in Cayrel de Strobel et al. (1997) range from −0.15 to +0.21 with a mean of +0.006 ± 0.105. An update of this list (Soubiran et al. 2010) gives 23 values with a mean of +0.037 ± 0.029. More recent values include +0.07 (Takeda et al. 2008), +0.11 ± 0.13 (Zieliński et al. 2012), 0.15 ± 0.2 (Jofré et al. 2014), +0.09 (Reffert et al. 2015), and +0.25 (Bluhm et al. 2016).

Similarly, numerous values of effective temperature and surface gravity have been assigned to the star. The means of the summary by Soubiran et al. (2010) are T_eff = 5002 ± 26 K and log g = 2.82 ± 0.01 dex, but values range from 4421 K to 5305 K and 2.60 to 3.22 dex. Line-depth ratios were used to find T_eff in four investigations: Strassmeier & Schordan (2000) used 15 ratios to find a mean of 4983 ± 41 K; Gray & Brown (2001) used five ratios to get 5058 ± 3 K; Kovtyukh et al. (2006) invoked 82 ratios resulting in 5079 ± 8 K; Biazzo et al. (2007) employed 15 pairs to get 5027 K ± 78 K. However, line-depth-ratio temperatures depend on external calibrations. Some of the more recent determinations of T_eff and log g for ε Vir, usually involving stellar-atmosphere modeling, are: 5044 K and 2.61 (Takeda et al. 2008), 5016 ± 28 K and 2.49 ± 0.09 (Zieliński et al. 2012), 4983 ± 61 K and 2.77 ± 0.02 (Heiter et al. 2015), 5077 ± 48 K and 2.77 ± 0.03 (Reffert et al. 2015), and 5236 K and 3.07 (Bluhm et al. 2016).

For the Fourier analysis in Section 5, only approximate values of the basic parameters are needed. Here, T_eff = 5000, log g = 2.7, and [Fe/H] = +0.04 are used.

Early radial velocity measurements ranged widely from −9.1 ± 2.8 (Lord 1898), −10.4 ± 1.9 km s⁻¹ (Lord 1905), through −12.5 ± 1.1 (Küstner 1908), −13.2 (Campbell 1913), to −14.8 ± 1.4 km s⁻¹ (Newall 1905). Wilson (1953) summarizes earlier values, listing −14.0 km s⁻¹. This same value is listed by Duflot et al. (1995). More recent values include −13.7 ± 0.3 (Beavers et al. 1979), −14.67 ± 0.14 (de Medeiros & Mayor 1999), −14.2 ± 0.3 (Gontcharov 2006), −14.38 ± 0.13 (Eaton & Williamson 2007), −14.56 ± 0.16 (Soubiran et al. 2008), −14.08 ± 0.16 (Massarotti et al. 2008), and −14.29 ± 0.02 km s⁻¹ (Jofré et al. 2015). In the light of the results given in Section 3, it seems likely that these velocity differences arise from the foibles of spectrographs and reduction procedures. And in Section 7, the absolute radial velocity of ε Vir, freed from the systematic error of granulation blueshifts, is derived from the third-signature plot.

The ¹²C/¹³C ratio for ε Vir is 20 ± 3 according to Tomkin et al. (1975), which is the expected value for stars prior to the mixing produced by the He flash.

Magnetic activity appears to be minimal. For example, Wilson & Bappu (1957) place ε Vir in the lowest category for HK emission strength and Strassmeier et al. (1990) list the star as not chromospherically active. Likewise, Rutten et al. (1991) look at chromospheric and coronal line strengths and find ε Vir has some of the lowest values of their stellar sample. Pasquini et al. (2000) find the K-line flux to be normal for its effective temperature and for its rotation rate. Using the rotation rate derived below in Section 5 places ε Vir in an even more central position in their correlation. Eaton (1995) found ${{\rm{H}}}_{\alpha }$ to be normal. Likewise, Dupree et al. (2007) find the Mg II h&k lines to be normal. More specifically, Pérez Martínez et al. (2011) find the Mg II h&k flux to be near the lower boundary of the stars they observed, while Pizzolato et al. (2000) determined the x-ray flux to be near the lower edge of their stellar sample. (This seems to be at variance with the value given by Huensch et al. 1996, where ε Vir lies near the upper edge of the x-ray values in their Figure 2.) Zirin (1976) looked for but found no He I λ10830 line.

Mark III interferometer measurements of the angular diameter (Mozurkewich et al. 2003) gave 3.283 ± 0.033 mas or a linear radius of 11.86 ± 0.13 ${R}_{\odot }$ (π = 29.76 ± 0.14 mas). The earlier value of 3.23 ± 0.05 by Nordgren et al. (2001) is in basic agreement.

Projected rotation rates have been determined from line broadening by several authors. Fekel (1997), with an assumed value for macroturbulence, deduced v sin i = 3.2 km s⁻¹ from line half-width measurements. The extensive study of de Medeiros & Mayor (1999), used the cross-correlation method of Benz & Mayor (1984), to find v sin i = 2.3 ± 1.0 km s⁻¹. A somewhat higher value of 3.7 km s⁻¹ was found by Setiawan et al. (2004), who used the same cross-correlation technique and an empirical correction for macroturbulence. Hekker & Meléndez (2007) made a rough approximation for the broadening of macroturbulence and found v sin i = 1.69 km s⁻¹. Massarotti et al. (2008) also assumed indirect corrections for macroturbulence broadening and got v sin i = 0.0 km s⁻¹. Jofré et al. (2015) obtained v sin i = 1.40 ± 0.45 km s⁻¹ based on an empirical calibration of the full half widths of 13 lines and an assumed isotropic Gaussian macroturbulence. The first and only attempt at a Fourier analysis was Smith & Dominy (1979) at a time when the technique was very new. The average over 12 lines came to v sin i = 2.7 ± 1.1 km s⁻¹ with ζ_RT = 4.1 ± 1.1 km s⁻¹ (after scaling ζ_RT by $\sqrt[]{2}$ to place their value on the standard scale). A new and more complete Fourier analysis is presented in Section 5 below.

Little has been previously published concerning the granulation properties of ε Vir. The only measured value of macroturbulence dispersion is that of Smith & Dominy (1979), as just noted, and that preliminary value is lower than the average for a G8 giant by ∼1 km s⁻¹ (Gray 2005b). In a previous publication (Gray 2005a), the Fe i λ6253 line bisector was found to be normal and the blue-most part of the line bisector lies at a flux fraction, F/F_c, of 0.61, placing it in the middle of the correlation with M_V. New information on the star's granulation is presented below, including a more accurate value of macroturbulence dispersion, updated line bisectors, a third-signature plot, and flux deficit calculations.

This paper is the fifth in a series that uses high-resolution, high signal-to-noise data to determine projected rotation rates and granulation properties of evolved stars: Paper 1, β Gem (Gray 2014), Paper 2, ε Cyg (Gray 2015, 2016a), Paper 3, α Ser (Gray 2016b), and Paper 4, β Her (Gray 2016c). Pinning down some of the basic physical characteristics of the standard star ε Vir is the aim of this paper.

The coudé spectrograph at the 1.2 m Elginfield Observatory (Gray 1986b, 2005b) was used to acquire 107 exposures over the interval from 2000.11 (JD 2451582.91) to 2010.44 (JD 2455355.61). The conventional entrance slit was replaced by a Richardson image slicer (Richardson 1966; Gray 2005b) that partially alleviated the less-than-perfect seeing at the Elginfield site. The nominal resolving power of the spectrograph is 10⁵. The light detector was a CCD with 200 by 4096 pixels 15 μm square. Exposure times ranged from 7.5 minutes to two hours with a mean of 1.3 hr. Based on photon count, signal to noise ratios (S/Ns) range from 125 to 627 with a mean of 352 and a median of 353. The continua were normalized to unity using the highest portions of the spectra. An example of an exposure is presented in Figure 1. Also in this figure is an exposure of β Her from Paper 4. The wavelength scale of the β Her exposure has been altered to better compare line strengths of the two stars. Although β Her is more than half a magnitude brighter than ε Vir, the two stars have nearly the same temperature, and the different line strengths arises primarily from different metallicities, [Fe/H] ∼ +0.04 for ε Vir versus −0.08 for β Her. The modest wavelength span of ∼54 Å and the limited number of lines is compensated for by high S/N and the stability of the spectrograph.

Zoom In Zoom Out Reset image size

The wavelength scale was determined using water-vapor lines formed within the coudé spectrograph with wavelengths given by Chevillard et al. (1989). The method is described in Gray & Brown (2006). Thirty-six of the 107 exposures were taken before the absolute-wavelength-calibration system was in place, leaving 71 calibrated exposures. Uncalibrated exposures are still quite suitable for determining line-depth ratios and for line profile analysis.

The instrumental profile of the spectrograph was measured numerous times using λ5461 from an isotopic ¹⁹⁸Hg lamp (Gray 2005b). An average profile was used in the Fourier analysis discussed below in Section 5.

Core positions of 46 lines per exposure were measured on the 71 exposures having a calibrated wavelength scale. Rest wavelengths are based on Nave et al. (1994) for Fe i lines with additional non-Fe i wavelengths from (Gray & Pugh 2012). Eleven of the lines have no absolute wavelengths. These extra lines improve (slightly) the mean radial velocities but forfeit the absolute values. Since variation in velocity is being investigated, this is appropriate; the absolute velocity is determined in Section 7. A mean velocity for each exposure was computed using weights for each line that were inversely proportional to the scatter shown by each line across the 71 exposures. Season means are displayed in Figure 2. The standard deviation of the nine season means about the horizontal dashed line is 18 m s⁻¹. This is smaller than the average standard deviation for the individual seasons, implying no detectable variation from season to season. It is also pushing the limit of the spectrograph capabilities (Gray & Brown 2006). A least-squares line through these points has a non-significant slope of −1.1 ± 2.4 m s⁻¹ per year. In short, the radial velocity of ε Vir is constant to a few m s⁻¹ over year and decade timescales. Concurrent evidence is found in the recent results by Yılmaz et al. (2013) that show ε Vir to have no variations exceeding 11 m s⁻¹ over a 2.4-year span in 2008–2010. The large range in radial velocity reported in the literature and commented on in Section 1 are therefore unlikely to be real, although obviously there is some risk in projecting the results from the recent decade back a full century.

Zoom In Zoom Out Reset image size

Line-depth ratios (LDRs) consist of the core depth of a temperature-sensitive line divided by the core depth of a temperature-stable line. As long as the lines being ratioed are of similar strength, first-order effects of small changes in spectrograph resolving power and zero-level errors cancel out (Gray & Brown 2001). In this investigation, 11 line pairs are used. Specific line information is given in Table 1 of Paper 1. The temperature sensitivity, dLDR/dT, of each ratio was determined using a set of stars having a range in temperature. Because no absolute wavelength calibration is required for this part of the investigation, we can include exposures from all 11 seasons. The 11 LDRs were converted to temperature differences by subtracting off the mean LDR over the 11 seasons and dividing by the sensitivity. The 11 ΔTs from each exposure were then averaged to get a relative temperature for each of 108 exposures. The season mean ΔT values are shown in Figure 3. The scatter of individual exposure means within seasons has an average of 2.8 K. The rms scatter of the 11 season-mean values is 0.72 K.

Zoom In Zoom Out Reset image size

A slow secular rise or a small ∼1 K amplitude oscillation with ∼10 year duration cannot be ruled out. A least-squares line shows a slope of 0.15 ± 0.05 degrees per year. However, as seen in the error bars of Figure 3, all of the season means are within error of zero variation.

To further investigate any variability, the 1990–1993 HIPPARCOS photometry was searched and may show variations in season means ∼5 m mag. A temperature variation ∼5 K would be needed to produce such a change in brightness. Bearing in mind the data in Figure 3 is taken a decade after the HIPPARCOS measurements, no temperature variation even remotely close to 5 K is seen. This also rules out rotational modulation. On the other hand, if the brightness variation arose from a change in radius, a ΔR ∼ 0.25% is implied. With a radius $\sim 12\,{R}_{\odot }$, and a timescale ∼1 yr, the velocity of the surface would be only ≲0.7 m s⁻¹, well below the levels of detection for my observations. Consequently, small radius variations remain a faint possibility. Given the stability of the star on every other front, this seems unlikely. As noted in Section 1, activity indices of ε Vir were low both before and after the HIPPARCOS observations. Probably the star is photometrically stable.

Rotation and macroturbulence cause most of the broadening in ε Vir spectral lines. Thermal broadening is smaller, particularly in the weaker lines. Sixteen profiles (tagged in Figure 1) from 15 of the best exposures spread over the decade of observations were selected and averaged. In principle, based on photon count, the cumulative s/n ratio would be ∼1700. In practice, line blending, continuum-setting errors, and related issues limit the S/N to somewhat smaller values. Blend corrections were made by reversing the profile on itself and using the unblended side to reconstruct the blend-damaged portion.

Fourier transforms are used to analyze the broadening and shapes of the spectral lines, and from this analysis the projected rotation rate, v sin i, and the radial-tangential macroturbulence velocity dispersion, ζ_RT are determined. The Fourier analysis consists of dividing the transform of the model photosphere-computed thermal component of the line into the transform of the observed, blend corrected profile. Implicit here is the assumption of no center-to-limb variation in the shape of the thermal profile. The result is a residual transform that embodies the Doppler shifts of rotation, macroturbulence, and the instrumental profile of the spectrograph. Thermal profiles were computed using the temperature distribution from Ruland et al. (1980, see also Paper 1) scaled to T_eff = 5000 K, based on the discussion in Section 1 above. As also stated in Section 1, the other adopted parameters are log g = 2.7 and [Fe/H] = +0.04.

For stronger lines, where the first sidelobe can be seen in the transforms, the first zero can be used to fix a value for the microturbulence dispersion, ξ. Microturbulence dispersion could be determined in this way for the three strongest lines: λ6253, ξ = 1.53, λ6246, ξ = 1.00, and λ6265, ξ = 0.96 km s⁻¹. Generally larger values are found for stronger lines. Note that while microturbulence is assumed to be isotropic in the usual manner, rotation and macroturbulence are not isotropic and require disk integrations to combine their Doppler shifts, as discussed below in this section (see also Paper 2, Section 5).

If everything worked perfectly and in a noiseless situation, all residual transforms should be the same. Figure 4 shows that this is not far from the truth, as the actual residual transforms do show substantial agreement. Naturally toward higher frequencies, the residual transforms are noisier owing to (1) the lower amplitudes in the transforms of the observed profiles and (2) division by smaller amplitudes in the thermal profile transforms. The white-noise levels can be seen in the transforms of the observed profiles for frequencies above ∼−0.5 dex. Amplified noise dominates the residual transforms for frequencies above ∼−0.7 dex. The mean of the residual transforms in Figure 4 is shown in Figure 5, where it is divided by the transform of the instrumental profile and fitted with a disk-integrated "model" of the combined Doppler shift of radial-tangential macroturbulence (Gray 2005b) and rotation. The error bars are computed from the scatter of the residual transforms. The standard configuration for the radial-tangential macroturbulence is used, namely, equal areas and equal dispersions for the radial and tangential components. Limb darkening was computed explicitly for the model photosphere with the parameters given above.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The solution is

$$\begin{eqnarray*}&&v\,\sin \,i=3.06\pm 0.20\ \mathrm{and}\ {\zeta }_{\mathrm{RT}}=5.16\pm 0.08\,\mathrm{km}\,{{\rm{s}}}^{-1},\end{eqnarray*}$$

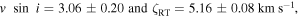
where the errors are estimated by computing other models differing by ∼ the error bars in Figure 5. These errors are only the "fitting" errors, specifying the uncertainty in fitting the disk-integration model to the observations. Conceptual error or inadequacies in the model are not included.

Figure 6 shows four examples of the model compared to the original observations. Here, the solid line gives the Fourier result convolved with the thermal and the instrumental profile. Although not perfect, the agreement is acceptable.

Zoom In Zoom Out Reset image size

The current Fourier solution agrees with the values found in the much earlier Fourier analysis of Smith & Dominy (1979) within their errors. However, the new values have errors ∼5 times smaller for v sin i and ∼14 times smaller for ζ_RT. The rotation rate of 3.06 km s⁻¹ agrees with the trend first shown in a previous investigation (Gray 1989). The macroturbulence dispersion of 5.15 km s⁻¹ is in accord with this 1989 investigation and Gray (2005b, Figure 17.10). Based on this rotation rate, the rotational period is less than ∼200 days or 0.54 years, assuming the radius is 11.86 solar radii.

As expected from its position in the HR diagram, the ε Vir Fe i λ6253 shows the classical "C" shaped bisector. When placed on Figure 8 of Paper 3, it is nearly identical with the bisector for ε Cyg (K0 III). The blue-most point on the ε Vir bisector is at F/F_c = 0.59, consistent with the earlier determination of 0.61 (Gray 2005a), and consistent with the correlation between the flux level of the blue-most point and absolute magnitude. Decoding of the bisector shape to yield information about the granulation contrast is done below in Section 8.

The empirical evidence that weaker lines experience stronger blueshifts is now well established for F, G, and K stars (Gray 2009; Gray & Pugh 2012, Papers 1–4, and earlier references they contain). This third signature of granulation is a measure of the drop off in granulation velocities with height, the cores of stronger lines being formed higher in the photosphere than the cores of weaker lines. The third-signature plot for ε Vir, with the core positions for 27 lines, is shown in Figure 7. These values are the means from 66 exposures, and the error estimated from the scatter, being generally comparable to the symbol size, is show at the left of the diagram. Errors range from 15 to 29 m s⁻¹, with a mean of 20 m s⁻¹ and are noticeably smaller than the actual velocity scatter of the points around the standard curve, a result of line blending and errors in standard wavelengths. The standard curve is taken from earlier work (Gray 2009). The shape comes from the composite data of numerous stars and the velocity zero point is calibrated against the Sun. The standard curve has been scaled and shifted in velocity to match the ε Vir observations. The two dashed curves, which indicate the sensitivity and approximate uncertainty, show the cases with the velocity scale factor changed by 0.2 either way from the adopted value of 1.10.

Zoom In Zoom Out Reset image size

The scale value of 1.10 implies that the granulation velocities in the photosphere if ε Vir are 10% larger than the solar values. K giants show a considerable range in scale factor from low values ∼0.5 (α Hya, K3 II-III; α Ser, K2 III) to high values ∼1.5 (η Dra, G8 III; α Boo, K2 III). The reason(s) or controlling factors may become clear as more stars are measured. The range of blueshifts in Figure 7 is ∼700 m s⁻¹. Because the upper end of this span is at zero, this is a lower limit on the average granule rise velocity. The true value is larger owing to (1) the redshifted light from the lanes contributing to the line profile and thereby reducing the full blueshift from the granule velocities and (2) the fact that the observed shifts are disk-integrated values, i.e., rise and fall velocities near the limb produce negligible Doppler shifts.

The −14,120 m s⁻¹ shift of the standard curve is the radial velocity of the star with the convective blueshifts fully accounted for. The uncertainty in this value is ∼75 m s⁻¹. Approximately equal contributions to the error arises from the fitting of the standard curve to the observations in Figure 7 and from the basic uncertainty in the zero-point calibration of the standard curve itself. The gravitational redshift can only be estimated since the mass is not explicitly known, but it is expected to be ∼140 m s⁻¹ if the mass is 2.6 and the radius is 11.86 solar units. Although according to Figure 7, one might expect previously published values that ignore the blueshifts to be too negative by ∼500 m s⁻¹, depending on the distribution of line strengths actually used in the measurements, only the value of de Medeiros & Mayor (1999) fulfill this expectation. Surprisingly, as summarized in Figure 8, other recent values are much closer to the third-signature result. In the investigation by Massarotti et al. (2008), the zero point is corrected using orbital dynamics of minor planets. In principle, this should remove the third-signature error at least to first order, and we see in Figure 8 that it has done so. A more complete discussion of radial velocity zero points would take us too far afield.

Zoom In Zoom Out Reset image size

As explained in previous papers in this series and in the original paper on bisector mapping (Gray 2010), the deviation of line bisectors from the third-signature plot is interpreted as a result of the imbalance between the light from granules versus lanes. The line profile, which is viewed as an approximation to the disk-integrated granulation velocity distribution, is manipulated to force the observed bisector to be mapped on to the third-signature plot. The right side of the profile is raised to make this happen, as illustrated in Figure 9 for Fe i λ6253. The quantitative measure of the imbalance is the flux deficit, i.e., the difference between the observed and mapped profiles, shown in panel (a). It has been normalized by the core depth of the profile (0.7218) so that it can be thought of as the fractional distortion of the velocity distribution. The normalized peak is 0.128 or 12.8% of the core depth.

Zoom In Zoom Out Reset image size

The deficit area is 12.9% of half the equivalent width of the line. Assuming equal areas for granules and lanes, a temperature difference of 134 K would produce the 12.9% difference. However, the true temperature difference is likely larger owing to the overlap of the granule and lane velocity distributions and the blurring of values from different limb positions. The assumption of equal areas for granules and lanes is suggested by solar observations (Sánchez Cuberes et al. 2000) and model calculations (e.g., Tremblay et al. 2013, Figure 17). The deficit area for ε Vir is typical of values found for other GK giants in the previous papers in this series. Further, the detailed shape of the deficit curve is very similar to those found previously for giants. The reader is referred to Figure 12 in Paper 4; the curve for ε Vir is within error of the β Her curve shown there. See Gray (2010) for a wider scope of deficit differences among stars. Rather similar values are found for theoretical granulation contrasts such as those by Tremblay et al. (2013): ∼10% for main-sequence models up to ∼18% for models with log g = 2.5. These numbers are computed for a portion of the stellar surface and integration over the stellar disk is not included.

Similar though they may be, significant differences can be seen in the flux deficits of giants. The change of the velocity position of the deficit with absolute magnitude as shown in Figure 10 for the GK giants that have been measured. More recent values, based on numerous exposures and therefore better determined, are shown as larger symbols, while provisional values from earlier publications are shown as smaller symbols. Unpublished values for three Hyades giants are also shown. Panel (a) shows the position of the peaks, which, while easy to visualize, are hard to precisely measure as the slope is zero. The peak of the ε Vir deficit is at 5.2 km s⁻¹ (green dot). Owing to non-zero slope, a slightly tighter correlation is found using the velocity position halfway up the left side of the deficits (panel (b)). The brighter the star, the larger the deficit velocity. In other words, more luminous stars have a greater velocity difference between rising and falling flows in the granulation. Over the magnitude span shown in the figure, the change amounts to ∼0.75 km s⁻¹. Because this is a disk-integrated number, the true velocity differences will be somewhat larger. The general trend of larger granulation scales with lower surface gravity is also found in hydrodynamical model calculations (e.g., Tremblay et al. 2013).

Zoom In Zoom Out Reset image size

Three low-weight points in Figure 10 come from the Hyades giants (paper in preparation). They appear to lie systematically higher, but given the errors, this might not be significant.

Although not shown in Figure 10, there is some tendency for larger peak-amplitude deficits to lie below the line and smaller peak-amplitude deficits to lie above the line shown in the figure. If this trend is real, it implies that some additional variable is at work.

The stable velocity and temperature exhibited by ε Vir increase its stature as a standard star. The granulation properties macroturbulence dispersion, bisector shape, and third-signature and flux-deficit characteristics are all similar to those of other GK giants. Its rotation rate is normal for a late G giant, so one must ask why ε Vir is more stable than other giants otherwise like it. The star may be in a Maunder-like minimum of magnetic activity or an "off" stage in a rotostat cycle (Gray 1986a, 1988, 1989).

I thank M. Debruyne for many years of technical support at the Elginfield Observatory where the observations were taken and also thank the student observers who took some of the observations. I am grateful to the Natural Sciences and Engineering Research Council of Canada for financial support.