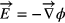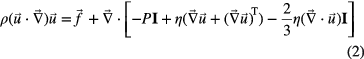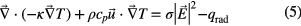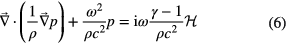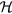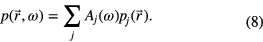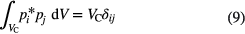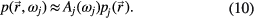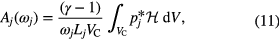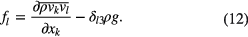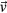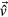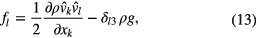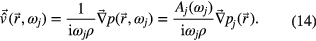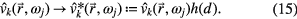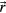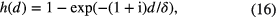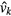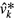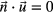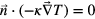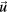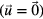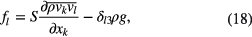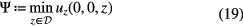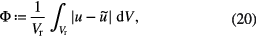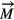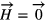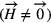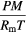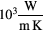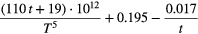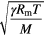Numerical investigation of symmetry breaking and critical behavior of the acoustic streaming field in high-intensity discharge lamps

The numerical investigation of light flicker in HID lamps requires a model that comprises a number of coupled equations that describe the processes inside the arc tube, at the arc tube's wall and the electrodes. In contrast to the time-dependent 2D model that describes an arc tube of infinite length [7], we use a stationary 3D model. Arc flicker shall be identified through instabilities of the velocity field.

The electric potential ϕ is determined from the equation of charge conservation

$$\begin{eqnarray}&&\vec{\nabla}\cdot (\sigma \vec{E})=0.\end{eqnarray} \tag{ 1 }$$

$\vec{E}=-\vec{\nabla}\phi$ is the electric field and σ the temperature-dependent electric conductivity⁴. The temperature dependency of σ and some other material coefficients is displayed in figure 2. At stable operation the velocity field $\vec{u}$ is purely buoyancy driven and can be calculated from the Navier–Stokes equation

$$\begin{eqnarray}&&\rho (\vec{u}\cdot \vec{\nabla})\vec{u}=\vec{f}+\vec{\nabla}\cdot \left[-P\mathbf{I}+\eta (\vec{\nabla}\vec{u}+{{(\vec{\nabla}\vec{u})}^{\text{T}}})-\frac{2}{3}\eta (\vec{\nabla}\cdot \vec{u})\mathbf{I}\right]\end{eqnarray} \tag{ 2 }$$

in combination with the equation describing mass conservation

$$\begin{eqnarray}&&\vec{\nabla}\cdot (\rho \vec{u})=0\end{eqnarray} \tag{ 3 }$$

(ρ density, P pressure inside arc tube, η dynamic viscosity, I identity martix). The buoyancy force density⁵

$$\begin{eqnarray}&&{{f}_{l}}=-{{\delta}_{l3}}\rho g\end{eqnarray} \tag{ 4 }$$

(δ_l3 Kronecker symbol, g  =  9.81 m s⁻²) bends the plasma arc upward off the symmetry axis if the lamp is operated horizontally. This loss of symmetry enforces the use of a 3D model. The temperature field T is determined from the Elenbaas–Heller equation

$$\begin{eqnarray}&&\vec{\nabla}\cdot (-\kappa \vec{\nabla}T)+\rho {{c}_{p}}\vec{u}\cdot \vec{\nabla}T=\sigma \mid \vec{E}{{\mid}^{2}}-{{q}_{\text{rad}}}\end{eqnarray} \tag{ 5 }$$

(κ thermal conductivity, c_p heat capacity at constant pressure, q_rad power loss density due to radiation). The domain of the Elenbaas–Heller equation comprises the inside of the arc tube, the electrodes and the wall. The geometry of the electrodes has been modeled with slight simplifications. The differential equations have to be supplemented by boundary conditions. These can be found in figure 3.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The equations above serve for the calculation of the distribution of the temperature and the power density of heat generation inside the arc tube. Both are necessary for the calculation of the acoustic pressure.

To obtain the acoustic pressure p inside the arc tube, we need to solve the inhomogeneous Helmholtz equation

$$\begin{eqnarray}&&\vec{\nabla}\cdot \left(\frac{1}{\rho}\vec{\nabla}p\right)+\frac{{{\omega}^{2}}}{\rho {{c}^{2}}}p=\text{i}\omega \frac{\gamma -1}{\rho {{c}^{2}}}\mathcal{H}\end{eqnarray} \tag{ 6 }$$

under the assumption that the walls of the arc tube are sound hard. The density ρ as well as the speed of sound c are temperature-dependent and, therefore, space-dependent quantities⁶. γ is the ratio of the heat capacities and $\mathcal{H}$ the power density of heat generation. In the present context we have

$$\begin{eqnarray}&&\mathcal{H}=\sigma \mid \vec{E}{{\mid}^{2}}-{{q}_{\text{rad}}}.\end{eqnarray} \tag{ 7 }$$

The inhomogeneous Helmholtz equation can be solved by an eigenmode expansion of the acoustic pressure [9, 10]:

$$\begin{eqnarray}&&p(\vec{r},\omega)=\underset{j}{\overset{{}}{\sum}} {{A}_{j}}(\omega ){{p}_{j}}(\vec{r}).\end{eqnarray} \tag{ 8 }$$

The eigenmodes are obtained by solving the homogeneous Helmholtz equation and normalize the solutions according to

$$\begin{eqnarray}&&{\int}_{{{V}_{\text{C}}}}p_{i}^{*}{{p}_{j}}\;\text{d}V={{V}_{\text{C}}}{{\delta}_{ij}}\end{eqnarray} \tag{ 9 }$$

(V_C is the volume enclosed by the walls of the arc tube). In this article the pressure at a certain resonance frequency ω_j is of interest. Under the assumption that the eigenfrequencies are well separated from one another the series above reduces to one term:

$$\begin{eqnarray}&&p\left(\vec{r},{{\omega}_{j}}\right)\approx {{A}_{j}}\left({{\omega}_{j}}\right){{p}_{j}}\left(\vec{r}\right).\end{eqnarray} \tag{ 10 }$$

The amplitude can be calculated from

$$\begin{eqnarray}&&{{A}_{j}}\left({{\omega}_{j}}\right)=\frac{(\gamma -1)}{{{\omega}_{j}}{{L}_{j}}{{V}_{\text{C}}}}{\int}_{{{V}_{\text{C}}}}p_{j}^{*}\mathcal{H}\;\text{d}V,\end{eqnarray} \tag{ 11 }$$

where L_j is the loss factor. How to estimate the loss factor, is described elsewhere [11]. Here, we consider volume loss due to heat conduction and viscosity as well as surface loss due to heat conduction and viscosity.

Fluid streaming around a rigid structure can generate noise. Less known is the opposite effect: Noise can produce fluid flow with a non-vanishing time average of mass transport. This nonlinear second order effect is called acoustic streaming [12].

If a standing pressure wave is excited in a closed vessel like the arc tube of an HID lamp, the particles of the fluid experience a viscous force, particularly those near the wall. The particles in immediate neighborhood of the wall are at rest and cannot participate in the oscillation (no-slip boundary condition). The viscosity induces a vortex-like motion of the arc tube filling inside the viscous boundary layer (inner streaming) [13]. Simultaneously, a second vortex-like motion is generated outside the boundary layer (outer streaming or Rayleigh streaming) [13]. The size of the outer streaming vortices is of the order of the wavelength of the standing pressure wave. Arc flicker is caused by the outer streaming vortices [5].

To obtain the streaming field, it is necessary to solve the Navier–Stokes equation with force density

$$\begin{eqnarray}&&{{f}_{l}}=\frac{\partial \overline{\rho {{v}_{k}}{{v}_{l}}}}{\partial {{x}_{k}}}-{{\delta}_{l3}}\rho g.\end{eqnarray} \tag{ 12 }$$

Here, Einstein's sum convention and time averaging over one cycle has to be applied. $\vec{v}$ is the sound particle velocity. For time harmonic waves the force density can be expressed by the amplitude $\overrightarrow{{\hat{v}}}$ of the sound particle velocity

$$\begin{eqnarray}&&{{f}_{l}}=\frac{1}{2}\frac{\partial \rho {{{\hat{v}}}_{k}}{{{\hat{v}}}_{l}}}{\partial {{x}_{k}}}-{{\delta}_{l3}}\rho g,\end{eqnarray} \tag{ 13 }$$

which can be calculated from the acoustic pressure [14]:

$$\begin{eqnarray}&&\overrightarrow{{\hat{v}}}\left(\vec{r},{{\omega}_{j}}\right)=\frac{1}{\text{i}{{\omega}_{j}}\rho}\vec{\nabla}p\left(\vec{r},{{\omega}_{j}}\right)=\frac{{{A}_{j}}\left({{\omega}_{j}}\right)}{\text{i}{{\omega}_{j}}\rho}\vec{\nabla}{{p}_{j}}\left(\vec{r}\right).\end{eqnarray} \tag{ 14 }$$

Using the acoustic pressure modes from section 2.2 for the calculation of the sound particle velocity is not sufficient for the determination of the streaming field. The reason is that the eigenmodes of the Helmholtz equation do not account for the no-slip boundary condition, which is essential for the formation of the streaming vortices. The solution to this problem is to multiply the sound particle velocity by a factor that is equal to one almost everywhere inside the arc tube and drops to zero at the wall [15]:

$$\begin{eqnarray}&&{{\hat{v}}_{k}}\left(\vec{r},{{\omega}_{j}}\right)\to \hat{v}_{k}^{*}\left(\vec{r},{{\omega}_{j}}\right){{\hat{v}}_{k}}\left(\vec{r},{{\omega}_{j}}\right)h(d).\end{eqnarray} \tag{ 15 }$$

Here d is the perpendicular distance of the point $\vec{r}$ to the wall. The function h(d) is defined by

$$\begin{eqnarray}&&h(d)=1-\text{exp}\left(-\left(1+\text{i}\right)d/\delta \right),\end{eqnarray} \tag{ 16 }$$

where the viscous penetration depth is

$$\begin{eqnarray}&&\delta =\sqrt{\frac{2\eta}{\rho {{\omega}_{j}}}}.\end{eqnarray} \tag{ 17 }$$

The function h(d) contains an oscillating and a damping factor. Instead of ${{\hat{v}}_{k}}$, the modified sound particle velocity $\hat{v}_{k}^{*}$ has to be used in the force term f _l of the Navier–Stokes equation.

Figure 5 shows the profile of the acoustic pressure mode we investigated in this paper. In Figure 6 the AS field associated with this mode is depicted. It has been obtained by the procedure described in section 4.2. Figure 7 shows the AS flow pattern due to a longitudinal acoustic mode in a closed cylindrical tube with a length equal to half a wavelength. This velocity field has been derived analytically about 75 years ago [15]. A close look at the flow pattern in the y–z-plane of figure 6 reveals the same structure as the one in figure 7—namely two vortices in the upper part and two vortices in the lower part (upper right and bottom left: clockwise; bottom right and upper left: counter-clockwise). The two systems are alike in principle but different in details like the shape of the vessel containing the fluid, the temperature and buoyancy force distribution in space as well as the pressure distribution of the acoustic mode. That we observe a similar structure of the flow patterns, indicates that the finite element model works properly.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Figure 6 shows a maximal AS velocity of approximately 0.61 m s⁻¹. Dreeben reported a maximal velocity of 1 m s⁻¹ from his 2D model [7]. The maximal buoyancy velocity in the 3D model is 8.5 cm s⁻¹ compared to 8 cm s⁻¹ in the 2D model. Since the investigated lamps are different with respect to geometry, wattage and other properties, this is a very satisfying accordance.

The AS field dominates over the buoyancy driven flow. It is clear that the physical conditions inside the arc tube change drastically once AS sets in. Under the influence of the altered flow field the arc moves to a new position and the temperature distribution changes substantially from the original field. Therefore, the space-dependent speed of sound and other physical properties also change. As a result the frequency of the eigenmode is changed and shifted away from the ac power frequency. The AS force diminishes or even vanishes. Temperature field, speed of sound and arc resume their original position and the process starts all over again, i.e. the arc flickers [5].

At present the feedback of AS on the temperature field is not included in the model. Nevertheless, the model can be used to investigate the influence of the AS field on light flicker. In a next step the calculations have to be repeated recursively to obtain the correct stationary fields. The AS force has to be calculated from the sound particle velocity of the previous step. Once convergence has been obtained, it would be interesting to investigate, whether the resulting flow field is stable or not. This can be accomplished with the aid of a linear stability analysis [16]. It seems natural to link the transition to instability with the onset of flicker. To solve the flicker problem directly with a transient FE model, is by orders of magnitude more demanding regarding computational requirements.

The flow pattern depicted in figure 6 is not mirror symmetric with respect to the x–z-plane (see figure 4). The model itself is symmetric and the question arises, how this asymmetry can be explained.

It is well known that in nonlinear dynamical systems, like the one under investigation here, far from thermodynamic equilibrium symmetry breaking can occur [16]. In these dissipative systems entropy is transfered to the surroundings and decreases locally. Famous examples are the Taylor vortices, which can appear in the gap between rotating cylinders (Taylor–Couette system), and the Rayleigh–Bénard system. In HID lamps bifurcation points of the current transfer to arc cathodes have been investigated [17, 18]. In these systems a symmetry gets lost once a certain control parameter exceeds a critical value.

In the Taylor–Couette and the Rayleigh–Bénard system the loss of symmetry is due to the exertion of opposing forces on the fluid elements. Taylor vortices form, once the centrifugal force prevails over the viscous force. In the Rayleigh–Bénard system certain structures emerge once thermal diffusion and viscous force are not able to balance the buoyancy force any more. In both cases a highly symmetrical state of the fluid becomes unstable and a phase transition of the second kind to a new state of less symmetry occurs. The new state is characterized by certain patterns depending on the system under consideration.

If standing waves are excited in a cylinder, the AS velocity field depicted in figure 7 develops. Once the acoustic pressure amplitude exceeds a critical value, the AS force is larger than the viscous force [15]. Before AS sets in, the fluid field $\vec{u}$ in the cylinder is identical to zero (continuous translational symmetry). Above the critical value a pattern of vortices is present (in a cylinder of infinite length this corresponds to a discrete translational symmetry).

In case of the HID lamp we observe a similar situation. Assume for the moment that the lamp is operated in outer space, where there is no gravity and the buoyancy force is zero. Consequently, the fluid velocity $\vec{u}$ is zero inside the arc tube. Near an acoustic resonance the AS force might become large in comparison to the viscous force. Except for the shape of the vessel and the temperature variation inside the arc tube, the situation is similar to the standing waves in a cylinder. Thus, an instability from a translational symmetric state $(\vec{u}=\vec{0})$ to a new state, which shows a pattern of vortices, would be observed in outer space due to the interaction of the AS and the viscous forces. The detailed appearance of the vortex pattern depends on the acoustic mode under consideration.

In the following it is assumed that the lamp is operated horizontally under the influence of gravity. We calculated a series of AS fields with the force term

$$\begin{eqnarray}&&{{f}_{l}}=S\frac{\partial \overline{\rho {{v}_{k}}{{v}_{l}}}}{\partial {{x}_{k}}}-{{\delta}_{l3}}\rho g,\end{eqnarray} \tag{ 18 }$$

where 0  ⩽  S  ⩽  1 is used as a control parameter. This could be realized experimentally by shifting the ac frequency away from the resonance frequency or lowering the modulation depth [19]. This should have the same effect, namely the reduction of the AS force. For S  =  0 (no AS) the fluid elements in the center of the arc tube experience the buoyancy force in upward direction, which results in the formation of two vortices.

For S  >  0 the AS force in the centrical upper part of the arc tube amplifies the upward movement of the fluid elements⁷. In the center of the lower part, however, the AS force tends to move the fluid elements downward, i.e. buoyancy and AS force point in opposite directions. Once the AS force is strong enough, two additional vortices appear. The formation of these additional vortices requires that the vertical velocity component of the fluid velocity is negative on parts of the z-axis. Therefore, we use

$$\begin{eqnarray}&&\Psi\underset{z\in \mathcal{D}}{{\min}} {{u}_{z}}(0,0,z)\end{eqnarray} \tag{ 19 }$$

as an order parameter for this type of pattern formation. $\mathcal{D}$ is the part of the z-axis inside the arc tube. In figure 8 the order parameter Ψ is depicted as function of the control parameter S together with the value of z where the minimum of u_z occurs. As expected from the reasoning above, the velocity u_z is non negative at low values of S (dominance of buoyancy) and becomes negative when S increases (dominance of AS). A negative value of Ψ indicates that the original state has become unstable and two additional vortices have been created. The value of the control parameter, at which the order parameter Ψ becomes negative, is called critical point. From the figure we conclude that the critical point for this type of instability is near 0.05⁸.

Zoom In Zoom Out Reset image size

Figure 8 reveals that the flow behavior changes at S  ≈  0.7. In the following we show that the jump of Ψ(S) is related to the loss of the mirror symmetry. To quantify the loss of symmetry, a second order parameter is introduced. We choose

$$\begin{eqnarray}&&\Phi:=\frac{1}{{{V}_{\text{r}}}}{\int}_{{{V}_{\text{r}}}}\mid u-\tilde{u}\mid \;\text{d}V,\end{eqnarray} \tag{ 20 }$$

in which the integral is over the right half of the interior of the arc tube. u(x, y, z) is the absolute value of the fluid velocity and (x, y, z) is u(x,−y, z). Φ measures the averaged difference of the velocities at the opposing points (x, y, z) and (x,−y, z) inside the arc tube. Therefore, the value of Φ is a measure for the asymmetry. In the symmetric phase Φ is zero. In the case of broken symmetry Φ assumes a positive value. The value of the control parameter, at which symmetry breaking sets in, is a second critical point.

The order parameter Φ has been calculated as a function of S. For S  >  0.7 the function Φ(S) manifests erratic fluctuations, indicating that the system has become unstable. In order to search for stable solutions, we calculated the flow field for a slightly tilted lamp (tilt angles α  =  ±10°,±  5°,±  4°,±  3°,±  2° and  ±  1°). The asymmetrical solutions resulting from the tilting have been used as initial conditions for the calculation of the AS flow field of the lamp operated at the next lower tilt angle. For the horizontally operated lamp (α  =  0) the asymmetry in the initial condition leads to the stable asymmetrical solution depicted in figure 6. The order parameters Φ obtained by approaching the horizontal lamp position from positive and from negative tilt angles are depicted in figure 9. For S  ⩽  0.7 the values of Φ are small and the solutions are symmetric (see figure 10). Figure 9 clearly shows that the symmetry gets lost at S  ≈  0.7.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The data for S  >  0.7 have been fitted to a(S  −  S_crit)^β. β is called critical exponent of the order parameter. The fit of the simulation results to the power law is excellent. The upper curve yields S_crit  =  0.716 and β  =  0.339, the lower curve yields S_crit  =  0.740 and β  =  0.316. The corresponding mean values are 0.728 and 0.3275.

The fit curves give the impression that the upper and the lower curve differ substantially, but the difference is due to the values at S  =  0.75 only. All other data in the upper and the lower part are not far apart from each other. An explanation for the difference at S  =  0.75 might be that the slight asymmetry in the FE mesh results in an amplification effect near the singularity.

The transition at the critical point leads from a mirror symmetric state to a state which does not show mirror symmetry. By tilting the lamp slightly to either side of its horizontal position, it is possible to choose between two equivalent flow states (pitchfork bifurcation). The situation is quite similar to the one of a ferromagnetic material in an external magnetic field $\vec{H}$ ⁹. For S  <  S_crit the flow field corresponds to a ferromagnet in the paramagnetic phase (T  >  T_Curie). The magnetization $\vec{M}$, which plays the role of the order parameter, assumes values that are dictated by the external field $\vec{H}$. In the case of the HID lamp the tilt angle α (or the lateral component of the buoyancy force) determines the value of the order parameter Φ. S  >  S_crit corresponds to the ferromagnetic phase (T  <  T_Curie). The order parameter Φ respectively the magnetization $\vec{M}$ assumes values different from zero, even for α  =  0, respectively $\vec{H}=\vec{0}$.

The most prominent microscopic model for a ferromagnet is probably the Ising model [21]. For the Ising model in three dimensions the generally accepted value of the critical exponent β is 0.3265 [22]. The difference of this value to our mean value of 0.3275 is 0.31%. This is remarkable. However, it seems questionable if the coincidence of the two values has any significance. The two systems are quite unlike and most probably belong to different universality classes.

For α  ≠  0 $(\vec{H}\ne \vec{0})$ the order parameters have contributions from symmetry breaking and from the external field respectively from lamp tilting as well. For the HID lamp the situation is illustrated in figure 11. When tilting the lamp for S  >  S_crit from positive values of α to negative values or vice versa, a first order phase transition takes place (figure 12).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size