Abstract
The sheath physics of radiofrequency plasmas excited by a sinusoidal waveform is reasonably well understood, but the existing models are complicated and are not easily extended to the more complex waveforms recently introduced in applications. Turner and Chabert (2014 Appl. Phys. Lett. 104 164102) proposed a model for collisionless sheaths that can easily be solved for arbitrary waveforms. In this paper we extend this model to the case of collisional sheaths in the intermediate pressure regime. Analytical expressions are derived for the electric field, the electric potential and the density profiles in the sheath region. The collisionless and collisional models are compared for a pulsed-voltage waveform.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Invited by Board Member Svetlana Starikovskaia
1. Introduction
Radiofrequency plasmas are widely used in the microelectronics industry [1, 2] and in many other applications, ranging from space propulsion [3, 4] through to medical applications [5–7]. In many instances, the most important phenomena take place in the radiofrequency sheaths, and it is therefore essential to model this boundary region appropriately. Historically, capacitive radiofrequency discharges were driven with a single-frequency sinusoidal waveform (typically at 13.56 MHz) and an accurate sheath model was derived for this case by Godyak [8] and Lieberman [9, 10].
In recent decades, it has become clear that more complex waveforms are needed to meet industrial needs. Dual-frequency excitation with two well-separated sinusoidal frequencies was used first [11]. Robiche et al [12, 13] extended the Lieberman model for this case, with the approximation of the small amplitude of the high-frequency component. However, more complex asymmetric waveforms were later introduced [14] (see also [15] and references therein for an extensive review) and the Lieberman sheath model could not easily be extended to these situations.
Two sheath models were introduced in recent years by Czarnetzki [16], and Turner and Chabert [17] to treat arbitrary waveforms. The latter was used by Lafleur et al [18] to treat the more general case of a capacitive discharge consisting of two asymmetric sheaths with self-bias formation. In this paper we revisit the Turner and Chabert model and extend it to collisional sheaths. We also give more detail on the derivation and on the information that can be extracted from this model. We do not discuss the validity of the key approximation that allows simple analytical expressions to be obtained, as this was discussed extensively in [17].
2. The radiofrequency sheath model
We consider a plasma with a density of  at the sheath edge, an electron temperature Te, and a single species of positive ions with mass M. We assume that the plasma fills the half-plane where x < 0, such that the sheath starts at x = 0, where a flux of ions given by
at the sheath edge, an electron temperature Te, and a single species of positive ions with mass M. We assume that the plasma fills the half-plane where x < 0, such that the sheath starts at x = 0, where a flux of ions given by

flows into the positive half-plane x > 0 (here  is the Bohm speed with e being the elementary charge and Te being expressed in volts). It follows that the sheath forms in the positive half-plane, and this sheath region will end at an electrode. The position of this electrode, denoted by sm, depends on the plasma parameters and on the voltage applied across the sheath.
is the Bohm speed with e being the elementary charge and Te being expressed in volts). It follows that the sheath forms in the positive half-plane, and this sheath region will end at an electrode. The position of this electrode, denoted by sm, depends on the plasma parameters and on the voltage applied across the sheath.
We now assume that some time-varying current density, J(t), flows through the plasma and the sheath, and we assume that the frequency spectrum of this current permits the assumption that ions passing through the sheath only respond to the time-averaged fields. Electrons, however, flow in and out of the sheath region as the current changes. In this case, we can identify a point s(t), such that at any given time there is a region of positive space charge where  and a region of quasi-neutral plasma where
and a region of quasi-neutral plasma where  . The point denoted as s(t) is understood to be the instantaneous sheath edge (this representation of the sheath is reasonable when
. The point denoted as s(t) is understood to be the instantaneous sheath edge (this representation of the sheath is reasonable when  ; a deeper discussion on this point can be found in [19, 20]). The time-averaged potential follows Poisson's equation
; a deeper discussion on this point can be found in [19, 20]). The time-averaged potential follows Poisson's equation

where  is the vacuum permittivity, and the time-averaged space charge is
is the vacuum permittivity, and the time-averaged space charge is

The electronic contribution to  is frequently important, and generally the time-averaged electron density
is frequently important, and generally the time-averaged electron density  will be the result of elaborate computations that present a major theoretical challenge. One practical approach is to make an approximation that includes the proper negative space charge within the sheath, without attempting an accurate representation of the spatial distribution of this charge. This aim is achieved by expressing the electron space charge as a constant fraction of the ion space charge,
will be the result of elaborate computations that present a major theoretical challenge. One practical approach is to make an approximation that includes the proper negative space charge within the sheath, without attempting an accurate representation of the spatial distribution of this charge. This aim is achieved by expressing the electron space charge as a constant fraction of the ion space charge,

where the dimensionless parameter ξ will be computed self-consistently from the control parameters. We then have
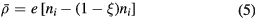

This approximation leads to mutually consistent solutions for both the time-averaged and the time-dependent sheath fields, without introducing any assumption about the time dependence of the sheath current or voltage. Note that in reality the time-averaged electron density is zero at the electrode and equal to the ion density at the sheath edge, and is thus a function of the position. However, as demonstrated in Turner and Chabert [17], the approximation is very good, whatever waveform is used. Consequently, we can couple this model to an arbitrary current or voltage waveform and proceed to construct a related sheath model without introducing any further approximations.
In figure 1, the time-averaged densities and potential in the sheaths are shown for  in the collisionless case, after equations (11) and (12), which will be derived below. In this figure the vertical line at s(t)/sm represents the instantaneous sheath position. We will now construct the solutions for both collisionless and collisional sheaths.
in the collisionless case, after equations (11) and (12), which will be derived below. In this figure the vertical line at s(t)/sm represents the instantaneous sheath position. We will now construct the solutions for both collisionless and collisional sheaths.
Figure 1. Time-averaged densities and potential in the sheaths for  in the collisionless case, after equations (11) and (12). The vertical line at s(t)/sm represents the instantaneous sheath position.
in the collisionless case, after equations (11) and (12). The vertical line at s(t)/sm represents the instantaneous sheath position.
Download figure:
Standard image High-resolution image2.1. Collisionless sheaths
2.1.1. The fields.
If the ions enter the sheath with a negligible velocity and are supposed to be collisionless, then energy conservation gives

and flux conservation implies

so that
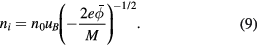
Equations (6) and (9) are combined to obtain Poisson's equation
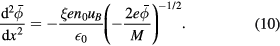
This is the equation used in the classical Child–Langmuir theory, with the space-charge reduced by the factor ξ, which can be easily integrated, as many textbooks show (see, for instance, [1, 2]). The solution reads

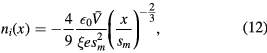
where
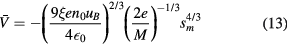
is the time-averaged voltage on the electrode at x = sm. The boundary conditions imposed in these solutions are  and
and  , and we note that
, and we note that  so that ni and sm are always positive. Equation (13) reduces to the usual collisionless DC Child law when
so that ni and sm are always positive. Equation (13) reduces to the usual collisionless DC Child law when  , but as can be seen, the sheath size sm will increase significantly when ξ decreases, i.e. when the electrons transiently neutralize the positive space charge for part of the radiofrequency cycle.
, but as can be seen, the sheath size sm will increase significantly when ξ decreases, i.e. when the electrons transiently neutralize the positive space charge for part of the radiofrequency cycle.
Now consider the situation where the electrode voltage varies in time and we wish to calculate the sheath potential at some instant. Then, using our step-front electron sheath model, the sheath region is divided into a quasi-neutral region that ends at x = s(t), and a positive space charge region for x > s(t), where
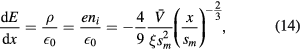
using equation (12). This equation can be integrated once to find the time- and space-varying electric field, using the boundary condition at E(x = s) = 0, yielding
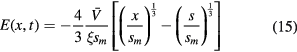
in the region where  . A second integration gives the time- and space-varying potential in the same region as
. A second integration gives the time- and space-varying potential in the same region as
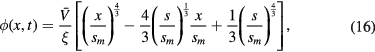
so that the instantaneous voltage at the electrode (at x = sm) is
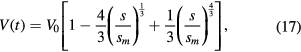
where we have defined the maximum voltage  , which occurs when s = 0. Hence we can write
, which occurs when s = 0. Hence we can write

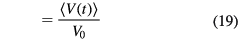
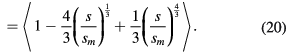
The value of ξ is therefore entirely defined by the sheath motion waveform, and consequently, as we shall see in the next section, by the radiofrequency current waveform.
2.1.2. Current–voltage characteristic of the sheath.
To relate the sheath voltage and the sheath position to the radiofrequency current, we simply note that within this model the current passing through the sheath is entirely displacement at the electrode, so that
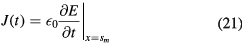
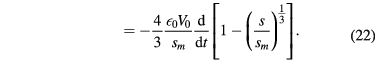
There is a physical constraint that J = 0 when s = 0 and s = sm. We choose the convention that s(t = 0) = 0. The current waveform must be chosen to be consistent with this convention, but this imposes no physically significant restrictions. Hence, the sheath position is defined solely by the radiofrequency current waveform J(t),
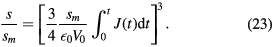
Since s/sm has a maximum value of unity, we must satisfy
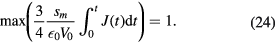
This equation defines the current–voltage characteristic of the collisionless sheath and is particularly useful for the widely used circuit model descriptions of capacitive discharges.
2.2. Collisional sheaths
2.2.1. The fields.
If we now consider an intermediate pressure regime in which the sheath is collisional, the ion motion becomes limited by collisions and the ion fluid velocity in the sheath becomes a function of the local time-averaged electric field [1, 2],

where  is the ion-neutral mean free path. Using ion flux conservation in the sheath, we obtain the ion density in the sheath as a function of the electric field,
is the ion-neutral mean free path. Using ion flux conservation in the sheath, we obtain the ion density in the sheath as a function of the electric field,
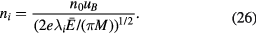
Gauss's law,
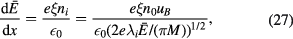
is integrated to obtain the time-averaged electric field in the sheath,
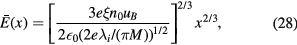
where we have used  (the electric field at the plasma–sheath interface) as a boundary condition. A second integration gives the time-averaged potential in the sheath,
(the electric field at the plasma–sheath interface) as a boundary condition. A second integration gives the time-averaged potential in the sheath,
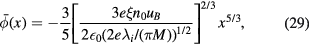
where we have again chosen  . We can now rewrite this expression in the following way,
. We can now rewrite this expression in the following way,
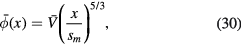
with
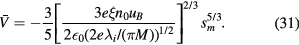
This is the collisional radiofrequency Child law. Combining equations (26), (28), and (31), we obtain the ion density in the sheath,
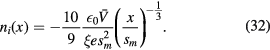
Following the same procedure as in the collisionless sheath case, we obtain the time-varying fields in the sheath, starting from Gauss's law,
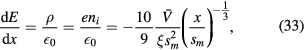
such that using E(x = s) = 0 we have
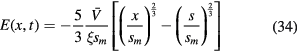
and
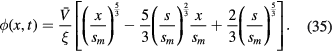
The instantaneous voltage at the electrode becomes
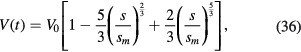
and consequently
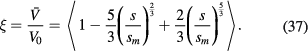
2.2.2. Current–voltage characteristic of the sheath.
The current passing through the sheath is now
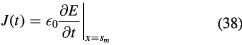
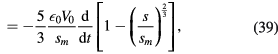
such that if s(t = 0) = 0, we obtain
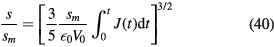
and the following condition must be satisfied:
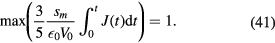
This equation defines the current–voltage characteristic of the collisional sheath.
3. Results for a sheath driven by a pulsed current waveform
The above expressions are completely general (within our fundamental approximation) and therefore independent of the radiofrequency current waveform used. In [17], single-frequency and dual-frequency sinusoidal waveforms were analyzed in the collisionless case and compared to particle-in-cell (PIC) simulations, showing excellent agreement. A pulsed-current waveform was also proposed as an example. In this paper we treat this latter case for both collisionless and collisional sheaths, with a discharge driven by a current density of the form
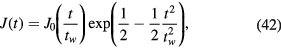
where the function has positive and negative extrema of  , separated in time by an interval 2tw. We assume that this pulse is repeated at intervals 2tp, supposed large enough that there is no appreciable interaction between successive pulses (
, separated in time by an interval 2tw. We assume that this pulse is repeated at intervals 2tp, supposed large enough that there is no appreciable interaction between successive pulses ( ). This type of waveform was recently proposed for self-bias generation and control on electrodes of equal areas [15]. As we shall see, the voltage waveform is close to a Gaussian peak in this case, such that the sheath voltage is small during most of the radiofrequency cycle and ξ is expected to be small when
). This type of waveform was recently proposed for self-bias generation and control on electrodes of equal areas [15]. As we shall see, the voltage waveform is close to a Gaussian peak in this case, such that the sheath voltage is small during most of the radiofrequency cycle and ξ is expected to be small when  . To solve the model, we start by evaluating the integral of the radiofrequency current,
. To solve the model, we start by evaluating the integral of the radiofrequency current,
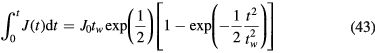
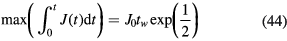
such that for the collisionless sheath case, using equations (23) and (24), we immediately obtain the sheath position waveform and the current–voltage characteristic,
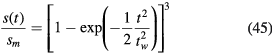
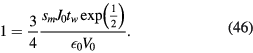
The value of ξ is then easily obtained,
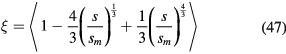
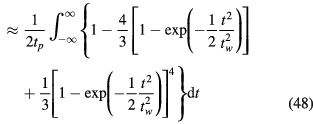
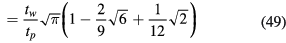
where we have used the fact that  so that the integration can be performed from
so that the integration can be performed from  to
to  . A similar analysis can be performed for the collisional sheath, with the following results
. A similar analysis can be performed for the collisional sheath, with the following results
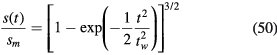
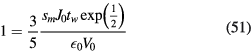
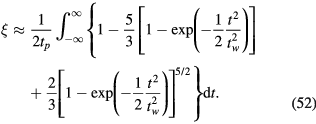
Figure 2 shows the evolution of the parameter ξ as a function of  . The solid line is given by equation (49) for collisionless sheaths, while the points are numerical integrations of equation (52) for collisional sheaths, which could not be integrated analytically. Consistent with the voltage waveforms in figure 3, ξ is almost independent of the model used. When
. The solid line is given by equation (49) for collisionless sheaths, while the points are numerical integrations of equation (52) for collisional sheaths, which could not be integrated analytically. Consistent with the voltage waveforms in figure 3, ξ is almost independent of the model used. When  increases, the voltage pulse becomes shorter, and as a consequence the portion of the time where the electrons fill the sheath grows larger. The time-averaged electron space charge therefore becomes comparable to the time-independent ion space charge and consequently ξ goes to zero, leading to a very large maximum sheath thickness for a given time-averaged voltage (according to equations (13) and/or (31)).
increases, the voltage pulse becomes shorter, and as a consequence the portion of the time where the electrons fill the sheath grows larger. The time-averaged electron space charge therefore becomes comparable to the time-independent ion space charge and consequently ξ goes to zero, leading to a very large maximum sheath thickness for a given time-averaged voltage (according to equations (13) and/or (31)).
Figure 2. Evolution of the parameter ξ as a function of  .
.
Download figure:
Standard image High-resolution imageFigure 3. Time variation of the sheath sizes (top) and the voltages (bottom) for a pulsed current from equation (42). The dashed lines are for collisionless sheaths, while the dotted lines are for collisional sheaths. The red line in the bottom panel is the voltage profile expected for a linear capacitor.
Download figure:
Standard image High-resolution imageThe time-dependent results of the collisionless and collisional sheath models are compared in figure 3. The sheath position as a function of the normalized time is shown in the top panel, while the voltage waveform is shown in the bottom panel. Significant differences are seen in the sheath position evolution, but these differences are smoothed out considerably in the voltage waveforms. In fact, the voltage waveforms are reasonably close to a Gaussian pulse, as shown in red in the figure. A Gaussian voltage pulse would be obtained for a truly capacitive sheath (a sheath modelled by a linear capacitor), for which the current pulse is proportional to the time derivative of the voltage pulse. The departure from the Gaussian accounts for the non-linear response of the moving sheath.
Although the voltage waveform seems to be mostly independent of the model used (collisional or collisionless), the maximum sheath thickness for a given time-averaged voltage is a function of the model used, and will vary significantly with collisionality. This is illustrated in figure 4, where the maximum sheath size, sm, is plotted as a function of the ion-neutral mean free path  . This figure has been obtained for argon ions with
. This figure has been obtained for argon ions with  m−3, a fixed-electron temperature Te = 3 V,
m−3, a fixed-electron temperature Te = 3 V,  , and
, and  V. The solid line is from collisional theory, equation (31), and the dashed line is the constant value from collisionless theory, equation (13). Collisional theory must be used for the short mean free path, but as can be seen, the two curves intersect at
V. The solid line is from collisional theory, equation (31), and the dashed line is the constant value from collisionless theory, equation (13). Collisional theory must be used for the short mean free path, but as can be seen, the two curves intersect at  , which may be seen as the limit where collisional sheath theory starts to fail. Alternatively, one may consider that collisional theory should be used when
, which may be seen as the limit where collisional sheath theory starts to fail. Alternatively, one may consider that collisional theory should be used when  ; this occurs for
; this occurs for  in the example of figure 4 (the gray area indicates the region where
in the example of figure 4 (the gray area indicates the region where  ). Note that in a self-consistent calculation Te would vary with
). Note that in a self-consistent calculation Te would vary with  , which would change the figure slightly.
, which would change the figure slightly.
Figure 4. Maximum sheath size as a function of the ion-neutral mean free path. The solid line is from collisional theory, equation (31), and the dashed line is the constant value from collisionless theory, equation (13). The gray area is the region where  . This figure has been obtained for argon ions with
. This figure has been obtained for argon ions with  m−3, Te = 3 V,
m−3, Te = 3 V,  , and
, and  V.
V.
Download figure:
Standard image High-resolution image4. Conclusion
In this paper, we have rehearsed the sheath model previously presented in [17] and extended it to the case of collisional sheaths in the intermediate pressure regime. The model relies on a simplifying assumption and is easily solved for any radiofrequency waveform, in the limit where the ions only respond to time-averaged fields. To illustrate the practical use of this model, we chose a pulsed-current waveform of interest for modern experiments. In this case, we found a significant difference in the time-resolved sheath position between collisional and collisionless sheaths. This difference is not as pronounced in the voltage waveform. However, the maximum sheath thickness for a given time-averaged voltage depends on the sheath collisionality, as seen in equation (31).




