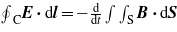Abstract
By introducing the mathematical concept of orientation, the significance of the minus sign in Faraday's law may be made clear to students with some knowledge of vector calculus. For many students, however, the traditional approach of treating the law as a relationship between positive scalars and of relying on Lenz's law to provide the information on the direction of the induced electromotive force may be a preferable pedagogical practice.
Export citation and abstract BibTeX RIS
1. Introduction
In a paper in this journal some years ago, Jones [1] provided a clear explanation of the origin and significance of the minus sign in the usual algebraic expression for Faraday's law. Unfortunately, many textbooks and papers continue to present the expression in a way that makes it difficult for students to fully understand the role played by the minus sign. This paper attempts to treat the same issues as were raised by Jones but from a rather different perspective.
2. The role of the minus sign
Faraday's law is commonly presented as stating that the induced electromotive force (emf) in a circuit is given by

where Φ is the magnetic flux through the circuit. Many authors explain away the minus sign on the right-hand side with a statement along the lines of 'the minus sign indicates that the induced emf opposes the change in flux' [2]. While strictly true under very specific conditions (to be discussed below), such statements provide little help to the learner attempting to come to terms with the physics involved and may even suggest that the minus sign is merely included as a sort of mnemonic3 to remind one of Lenz's law, which gives the sense or direction of the emf induced in the circuit.
For equation (1) to have any meaning, both εind and Φ have to be algebraic quantities4. For any quantity to be algebraic a convention of signs needs to have been adopted. Students approaching Faraday's law for the first time may well have experience of emf as an algebraic quantity (for example, when applying Kirchhoff's rules to multiloop circuits) and they will be aware that the choice of positive sense around a loop is completely arbitrary. Similarly, for such students the choice of what should be considered positive flux would appear to be equally arbitrary—a second and independent convention of signs being needed. For these students, the minus sign in (1) can have little or no meaning.
For more advanced students, however, who may have some knowledge of line and surface integrals, the significance of the minus sign is somewhat more easily grasped, although the issues involved are hardly non-trivial. In the language of vector calculus, the emf induced in a closed circuit (say the curve C in figure 1) can be defined as

where E is the electric field strength at the element dl (in a frame in which dl is at rest). Similarly, the magnetic flux through the circuit is defined as

where S is a simply connected surface bounded by the curve C, B is the magnetic flux density at the element of area dS = (dS)en (in a frame in which dS is at rest) and en is a unit vector perpendicular to the area element.
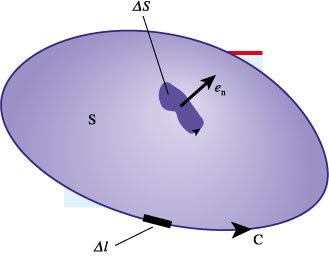
Figure 1. The figure shows a two-sided surface S bounded by the closed curve C. The (arbitrarily chosen) orientation of the curve C is indicated by the arrow. The convention for the positive direction of a normal to the surface S must be defined consistently with the chosen orientation of C for the minus sign in Faraday's law to be meaningful.
Download figure:
Standard image3. Conventions of signs
For εind and Φ to be interrelated algebraic quantities, as in equation (1), consistent conventions of signs are required—that is, a choice of positive direction of dl and a related choice of positive direction for en. What this boils down to is the adoption of what mathematicians call the orientation of the curve C and of the consistent induced orientation of the surface S.
Any closed curve can have two choices of orientation: either (i) as indicated by the arrow on the curve C in the figure or (ii) as indicated by the arrow reversed. An element dl is positive if it is pointing along the direction indicated by the choice of orientation. Again, there are two possible choices for the positive direction for the normal vector en—either directed as shown in figure 1 or directed in the opposite sense (that is, pointing away from the opposite side of the surface). If the minus sign in equation (1) is to have any meaning, the convention of signs for the positive direction for en must be chosen, relative to the choice of orientation of C, according to standard convention (see the mathematical details below).
With appropriately adopted conventions (and only in these circumstances), Faraday's law takes the form

Thus, given some thought and reflection and armed with the idea of orientation, students who have familiarity with line and surface integrals should be able to interpret the minus sign in Faraday's law correctly and apply it in specific situations5.
On the other hand, it is hard to see how most students encountering the principle of electromagnetic induction for the first time could find the minus sign in (1) in any way meaningful. In these circumstances it would appear to be pedagogically preferable for teachers to adopt the traditional approach of treating the induced emf as a positive scalar given by

and of relying on Lenz's law to provide the information on the sense in which the induced emf is directed around the circuit [4].
4. Mathematical details
Let S be a smooth, simply connected, orientable surface bounded by the simple closed curve C (figure 2). The requirement that a surface be orientable means that a continuous and differentiable normal vector field is defined everywhere on S. There are obviously two possible choices for the positive direction of this vector field (that is, for vectors erected normal to a specified side of the surface to be positive). The following construction describes the standard convention for making that choice—that is, for adopting the orientation of S induced by the orientation of C.
- (1)The (arbitrary) choice of the orientation of C determines the direction of the positively directed vectors tangent to C. Let e1 be such a positively directed tangent vector at some point P of C.
- (2)Choose an inward-pointing vector (e2, say) lying in the plane tangent to the surface S at P.
- (3)The vector en = e1 × e2 (the convention requires that the product be taken in the order specified) is a vector normal to S and its direction determines the induced orientation of the surface S consistent with the choice of orientation of C.
Figure 2. Construction of the orientation of the surface S induced by the orientation of the closed curve C. The vectors e1 and e2 are in the plane tangent to the surface at P and en = e1 × e2 is perpendicular to the surface.
Download figure:
Standard imageThis construction essentially determines the side of the surface away from which a positive normal vector is directed. If the orientation of the curve is reversed, vectors pointing away from the opposite side of the surface are positive and the minus sign in Faraday's law remains. If a different convention was adopted for the induced orientation (for example, an outward-pointing vector at P or en = e2 × e1 above), there would be no minus sign in Faraday's law.
Footnotes
- 3
See, for example, [3]: 'The minus signs ... are there to remind us in which direction the induced emf acts'.
- 4
An algebraic physical quantity has a sign, a magnitude and a unit; for example, at some instant the quantities might have values εind =− 5.1 V and Φ =+ 25 μWb.
- 5
Note that in the generalized form of Faraday's law,
 , C is any closed curve in space and S is any simply connected surface bounded by C.
, C is any closed curve in space and S is any simply connected surface bounded by C.
Biographies

Colm O'Sullivan is retired Associate Professor in Physics at University College Cork, Ireland. His research interests are in cosmic ray astrophysics and physics education. He is co-author (with Michael Mansfield) of the textbook 'Understanding Physics'.

Donal Hurleyis retired from the post of Senior Lecturer in Mathematics at University College Cork, Ireland. His research interests are in the area of differential geometry and he enjoys working with physicists on geometrical aspects of physics.