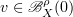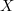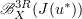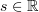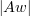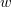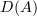Abstract
It is shown that the long-time dynamics (the global attractor) of the 2D Navier–Stokes system is embedded in the long-time dynamics of an ordinary differential equation, called a determining form, in a space of trajectories which is isomorphic to  for sufficiently large
for sufficiently large 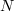 depending on the physical parameters of the Navier–Stokes equations. A unified approach is presented, based on interpolant operators constructed from various determining parameters for the Navier–Stokes equations, namely, determining nodal values, Fourier modes, finite volume elements, finite elements, and so on. There are two immediate and interesting consequences of this unified approach. The first is that the constructed determining form has a Lyapunov function, and thus its solutions converge to the set of steady states of the determining form as the time goes to infinity. The second is that these steady states of the determining form can be uniquely identified with the trajectories in the global attractor of the Navier–Stokes system. It should be added that this unified approach is general enough that it applies, in an almost straightforward manner, to a whole class of dissipative dynamical systems.
depending on the physical parameters of the Navier–Stokes equations. A unified approach is presented, based on interpolant operators constructed from various determining parameters for the Navier–Stokes equations, namely, determining nodal values, Fourier modes, finite volume elements, finite elements, and so on. There are two immediate and interesting consequences of this unified approach. The first is that the constructed determining form has a Lyapunov function, and thus its solutions converge to the set of steady states of the determining form as the time goes to infinity. The second is that these steady states of the determining form can be uniquely identified with the trajectories in the global attractor of the Navier–Stokes system. It should be added that this unified approach is general enough that it applies, in an almost straightforward manner, to a whole class of dissipative dynamical systems.
Bibliography: 23 titles.
Export citation and abstract BibTeX RIS
The work of the first author was supported by NSF (grant no. DMS-1109784), that of the second author by NSF (grant nos. DMS-1008661 and DMS-1109638), and that of the fourth author by NSF (grant nos. DMS-1009950, DMS-1109640, and DMS-1109645), as well as the Minerva Stiftung/Foundation.
Dedicated to the memory of Professor Mark Vishik
1. Introduction
The 2D system of Navier–Stokes equations (NSE), (2.1) and (2.2), in addition to being a fundamental component of many fluid models, is intriguing for several theoretical reasons. In featuring both a direct cascade of enstrophy and an inverse cascade of energy, it displays more complicated turbulence phenomena than does the 3D system of NSE [3], [19], [20]. Also unlike in 3D, the global existence theory for the 2D NSE is complete (see, for instance, [6], [22]). In fact, the long-time dynamics of the 2D NSE is entirely contained in the global attractor  (see (2.5)), a compact finite-dimensional subset of the infinite-dimensional phase space
(see (2.5)), a compact finite-dimensional subset of the infinite-dimensional phase space 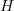 of solenoidal finite-energy vector fields, (see, for instance, [6], [10], [16], [22]). Sharp estimates of the dimension of the global attractor in terms of the relevant physical parameters were first established in [7] (see also [6], [21], [22] and references therein). If there were an inertial manifold
of solenoidal finite-energy vector fields, (see, for instance, [6], [10], [16], [22]). Sharp estimates of the dimension of the global attractor in terms of the relevant physical parameters were first established in [7] (see also [6], [21], [22] and references therein). If there were an inertial manifold 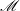 (that is, a Lipschitz, finite-dimensional, forward-invariant manifold which attracts each bounded set at an exponential rate), then
(that is, a Lipschitz, finite-dimensional, forward-invariant manifold which attracts each bounded set at an exponential rate), then  , and the dynamics on
, and the dynamics on  would be captured by an ordinary differential equation (ODE), called an inertial form, in a finite-dimensional phase space [6], [12], [13], [22]. This can be attained through reduction of the original evolution equation to an equation on the inertial manifold
would be captured by an ordinary differential equation (ODE), called an inertial form, in a finite-dimensional phase space [6], [12], [13], [22]. This can be attained through reduction of the original evolution equation to an equation on the inertial manifold  . Yet the existence of an inertial manifold for the 2D NSE has been an open problem since the 1980s!!
. Yet the existence of an inertial manifold for the 2D NSE has been an open problem since the 1980s!!
This is very surprising since there are even stronger indicators of the finite-dimensional behavior of the 2D NSE. The solutions in 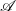 are determined by the asymptotic behavior of a sufficient (finite) number of determining parameters. If in the limit as
are determined by the asymptotic behavior of a sufficient (finite) number of determining parameters. If in the limit as  a sufficiently large number of low Fourier modes (or nodal values, or finite volume elements) for two solutions in
a sufficiently large number of low Fourier modes (or nodal values, or finite volume elements) for two solutions in 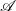 converge to each other, then the solutions coincide (see, for instance, [5] for a unified theory of determining parameters and projections). This is equivalent, at least in the case of Fourier modes, to the following:
converge to each other, then the solutions coincide (see, for instance, [5] for a unified theory of determining parameters and projections). This is equivalent, at least in the case of Fourier modes, to the following:
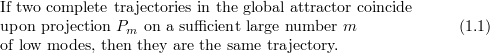
This notion of determining modes, which was introduced in [11] (see also, [18] for sharp estimates of the number of determining modes), was used in [8] to construct a system of ODEs in the Banach space  that govern the evolution of trajectories in the space
that govern the evolution of trajectories in the space  . We call the system of ODEs a determining form. Trajectories in the global attractor
. We call the system of ODEs a determining form. Trajectories in the global attractor  of the 2D NSE (2.2) are identified with travelling wave solutions of the determining form. There are conceptually two time variables in play for the determining form: the evolving time for the ODE and the original time variable of the NSE that now parameterizes complete trajectories in
of the 2D NSE (2.2) are identified with travelling wave solutions of the determining form. There are conceptually two time variables in play for the determining form: the evolving time for the ODE and the original time variable of the NSE that now parameterizes complete trajectories in  . Though the determining form has an infinite-dimensional phase space, the vector field that governs the evolution is globally Lipschitz, so the determining form is an ODE in the true sense. The key to constructing the determining form in [8] is to extend to the whole space
. Though the determining form has an infinite-dimensional phase space, the vector field that governs the evolution is globally Lipschitz, so the determining form is an ODE in the true sense. The key to constructing the determining form in [8] is to extend to the whole space  the map
the map  provided by (1.1) on the set
provided by (1.1) on the set  of complete trajectories in
of complete trajectories in  . The extended map is shown to be Lipschitz, and its image plays the role of recovering the higher modes, while the evolving trajectory in
. The extended map is shown to be Lipschitz, and its image plays the role of recovering the higher modes, while the evolving trajectory in  represents the lower modes.
represents the lower modes.
The determining form in this paper has an entirely different character. It is a system which possesses a Lyapunov function and whose steady states are precisely the trajectories in the global attractor of the 2D NSE. It is more general in that it can be used with a variety of determining parameters, including nodal values as well as Fourier modes. Furthermore, it provides a general framework and strategy that can be implemented for other dissipative systems. Like the determining form in [8], the key to its construction is the extension of a map  defined at first only for projections of trajectories in
defined at first only for projections of trajectories in  . This is done by using the feedback control term added to the NSE as suggested in [1] and [2], and this involves an interpolating operator
. This is done by using the feedback control term added to the NSE as suggested in [1] and [2], and this involves an interpolating operator  approximating the identity map at the level
approximating the identity map at the level  (for instance,
(for instance,  can be based on nodal values, where
can be based on nodal values, where  represents the grid size). This construction and the statements of our main results are presented in § 3. In § 2 we provide some preliminary background material and useful inequalities concerning the Navier–Stokes equations. Details of the proofs of our main results are given in §§ 4 and 5.
represents the grid size). This construction and the statements of our main results are presented in § 3. In § 2 we provide some preliminary background material and useful inequalities concerning the Navier–Stokes equations. Details of the proofs of our main results are given in §§ 4 and 5.
2. Functional setting and the Navier–Stokes equations
We consider the two-dimensional incompressible Navier–Stokes equations
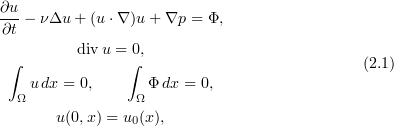
subject to periodic boundary conditions with the basic domain ![$\Omega =[0,L]^2$](https://content.cld.iop.org/journals/0036-0279/69/2/359/revision1/rms_69_2_359ieqn27.gif) . The velocity field
. The velocity field  and the pressure
and the pressure  are the unknown functions, while
are the unknown functions, while  is a given forcing term, and
is a given forcing term, and  is a given constant viscosity.
is a given constant viscosity.
Let
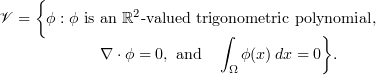
For any subset  we define
we define  . We denote by
. We denote by  and
and  the closures of
the closures of  in
in  and
and  , respectively. The inner product and norm in the Hilbert spaces
, respectively. The inner product and norm in the Hilbert spaces  and
and  will be denoted by
will be denoted by  and
and  , respectively, and the corresponding inner product and norm in the Hilbert spaces
, respectively, and the corresponding inner product and norm in the Hilbert spaces  and
and  will be denoted by
will be denoted by  and
and  . Specifically, for every
. Specifically, for every  we set
we set
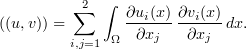
Let  denote the dual space of the space
denote the dual space of the space  .
.
Using the above functional notation, we can write the Navier–Stokes equations as an evolution equation in the Hilbert space  (cf. [6], [22]):
(cf. [6], [22]):
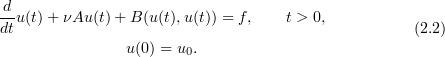
The Stokes operator  , the bilinear operator
, the bilinear operator  , and the force
, and the force  are defined as
are defined as
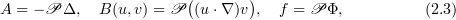
where  is the Helmholtz orthogonal projection from
is the Helmholtz orthogonal projection from  onto
onto  , and where
, and where  and
and  are smooth enough that
are smooth enough that  makes sense. In this paper we will assume that
makes sense. In this paper we will assume that  .
.
We remark that  . The operator
. The operator  is self-adjoint, with compact inverse. Therefore, the space
is self-adjoint, with compact inverse. Therefore, the space  possesses an orthonormal basis
possesses an orthonormal basis 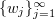 of eigenfunctions of
of eigenfunctions of  , namely,
, namely,  , with
, with  (cf. [6], [22]). The powers
(cf. [6], [22]). The powers  are given by
are given by
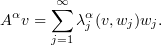
Note that all the powers of  commute with
commute with  . Note also that
. Note also that  and that
and that
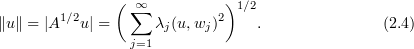
It is well known that the NSE (2.2) has a global attractor
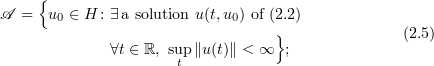
that is,  is the maximal bounded invariant subset of
is the maximal bounded invariant subset of  under the NSE dynamics, or equivalently it is the minimal compact subset of
under the NSE dynamics, or equivalently it is the minimal compact subset of  which uniformly attracts all bounded sets in
which uniformly attracts all bounded sets in  under the dynamics of (2.2). In particular, it is also known that
under the dynamics of (2.2). In particular, it is also known that
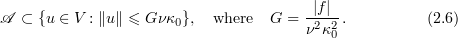
 is the Grashof number, a dimensionless physical parameter, and
is the Grashof number, a dimensionless physical parameter, and  . For the above properties see, for instance, [6], [10], [16], [22].
. For the above properties see, for instance, [6], [10], [16], [22].
Next, we introduce a number of identities satisfied by the bilinear term. This includes the orthogonality relations

(where  denotes the dual action between
denotes the dual action between  and
and  ), and
), and
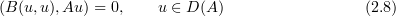
(see, for instance, [6], [10], [22]). The relation (2.7) implies that (cf. [6], [22])
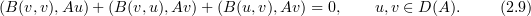
From now on,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  will denote universal dimensionless positive constants. Our estimates for the non-linear term will involve Agmon's inequality
will denote universal dimensionless positive constants. Our estimates for the non-linear term will involve Agmon's inequality
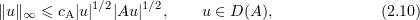
and the Sobolev and Ladyzhenskaya inequalities
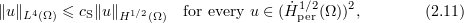
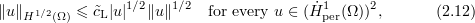
which imply that
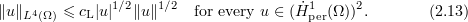
We also use the versions of the Poincaré inequality
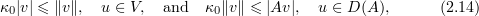
and Young's inequality
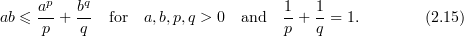
By (2.13)
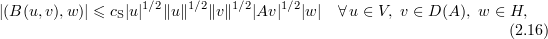
and by (2.10)
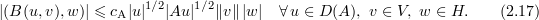
In addition,
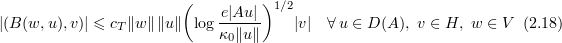
(see [23]). Using the Brézis-Gallouet inequality [4] (see also a different proof in [23]), we have
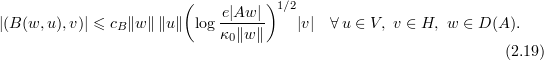
We also use the following modified Gronwall inequality from [17] (see also [10]).
Lemma 2.1. Let  and
and  be locally integrable real-valued functions on
be locally integrable real-valued functions on  which for some
which for some  satisfy
satisfy
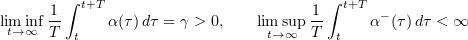
and
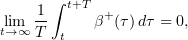
where 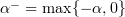 and
and  . Suppose that
. Suppose that  is an absolutely continuous non-negative function on
is an absolutely continuous non-negative function on  such that
such that
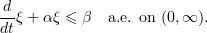
Then  as
as  .
.
Lemma 2.1 will be combined later with the following estimates for averaged solutions (see [17], [18]).
Proposition 2.2. Let  be a solution of the NSE (2.2) and let
be a solution of the NSE (2.2) and let  . Then
. Then
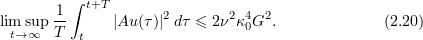
If  , then
, then
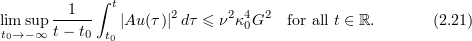
Moreover, it follows from the Cauchy–Schwarz inequality that
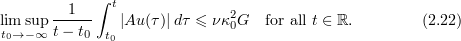
Proposition 2.3. Let  be a solution of the NSE (2.2). Then
be a solution of the NSE (2.2). Then
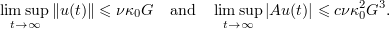
In particular,
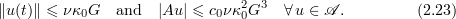
Moreover, the solutions in the global attractor  are analytic with respect to the time variable in a strip about the real axis with width
are analytic with respect to the time variable in a strip about the real axis with width  . In addition, by the Cauchy formula the above estimates imply that
. In addition, by the Cauchy formula the above estimates imply that
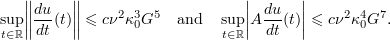
The ideas of the proof of the above proposition can be found in [6]. However, the new sharp estimates in Proposition 2.3 are obtained in [9].
We now derive two bounds for  .
.
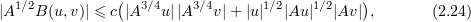
and for all  and
and 
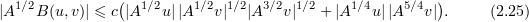
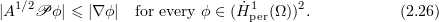
By virtue of (2.11) we have
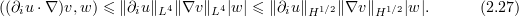
It follows from (2.26), (2.27), (2.10), and (2.12) that
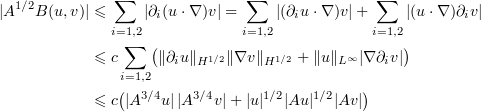
and
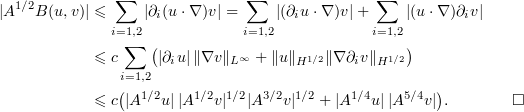
Inspired by the proof of the Brézis–Gallouet inequality [4], we establish below a bound for the  -norm which we later use to optimize an estimate.
-norm which we later use to optimize an estimate.
Lemma 2.5. Let  . Then for every
. Then for every 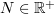
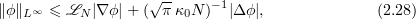
where  .
.
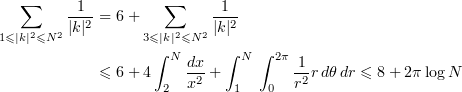
and for  ,
,
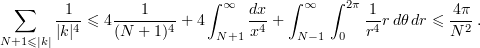
Using the Cauchy–Schwarz inequality and Parseval's identity, we have

3. Determining form and statements of main results
3.1. Interpolant operators.
In this subsection we introduce a unified approach for using various determining parameters (modes, nodes, volume elements, and so on) by representing them in terms of interpolant operators that approximate the identity.
Let 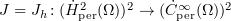 be a finite-rank linear operator approximating the identity in the following sense: for every
be a finite-rank linear operator approximating the identity in the following sense: for every  we have
we have  ,
,  has zero spatial average, and
has zero spatial average, and
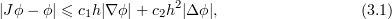
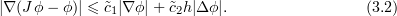
Here 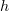 is a small parameter that determines the order of approximation. The rank of
is a small parameter that determines the order of approximation. The rank of  is of order
is of order  . For example, such interpolant polynomials are induced by the determining parameters of the NSE, such as determining modes, nodes, volume elements, projections of finite elements, and so on (see, for instance, [5], [11], [14], [15], [17], [18] and references therein). The most straightforward example of such interpolant operators is the projection operator
. For example, such interpolant polynomials are induced by the determining parameters of the NSE, such as determining modes, nodes, volume elements, projections of finite elements, and so on (see, for instance, [5], [11], [14], [15], [17], [18] and references therein). The most straightforward example of such interpolant operators is the projection operator  onto
onto  , where
, where  . Also, the appendix of [1] provides explicit examples of such interpolant operators that are based on nodal values and that satisfy (3.1) and (3.2). We remark that a general framework employing interpolant polynomials satisfying (3.1) was introduced in [5] for investigating the long-time dynamics of the NSE.
. Also, the appendix of [1] provides explicit examples of such interpolant operators that are based on nodal values and that satisfy (3.1) and (3.2). We remark that a general framework employing interpolant polynomials satisfying (3.1) was introduced in [5] for investigating the long-time dynamics of the NSE.
3.2. Determining form.
In this subsection we present a determining form that is induced by the interpolant operators  . The connection between the long-time dynamics of the NSE (2.2) and the determining form is explained in the following result.
. The connection between the long-time dynamics of the NSE (2.2) and the determining form is explained in the following result.
Proposition 3.1. Let  and let
and let  ,
,  , be a solution of the NSE (2.2) that lies in the global attractor
, be a solution of the NSE (2.2) that lies in the global attractor  . Suppose that
. Suppose that  with
with  satisfies the equation
satisfies the equation
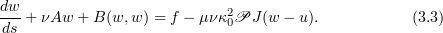
Then  if
if
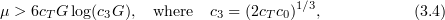
and  is small enough that
is small enough that
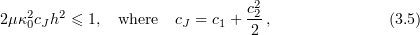
and and 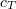 ,
,  ,
, 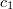 ,
, 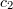 are as in (2.18), (2.23), and (3.1).
are as in (2.18), (2.23), and (3.1).
The proof of Proposition 3.1 is given in § 4. We remark that the existence of solutions of (3.3), as specified in Proposition 3.1, follows from Theorem 3.2 below.
Next, we introduce the phase space of the dynamics of our determining form. Let
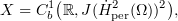
with the two norms
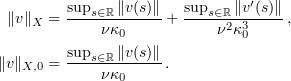
Now we let  be a given element of
be a given element of  and consider the equation
and consider the equation
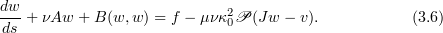
We show in the following result that under certain conditions on the parameters  and
and  , which depend on
, which depend on  , (3.6) has a unique bounded global solution
, (3.6) has a unique bounded global solution 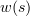 for
for  .
.
Theorem 3.2. Let  , and let
, and let  for some
for some  . Fix
. Fix  and
and  so that
so that
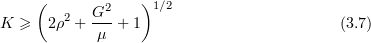
and
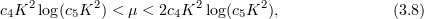
where  and
and  . Choose
. Choose  small enough so that
small enough so that

Then for every  equation (3.6) has a unique solution
equation (3.6) has a unique solution  that exists globally for all
that exists globally for all  and has the following properties:
and has the following properties:

Moreover, suppose that  and
and  and
and  are the corresponding solutions of (3.6). Let
are the corresponding solutions of (3.6). Let  and
and  . Then
. Then
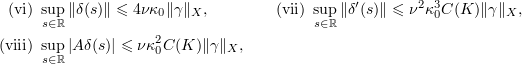
where 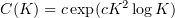 for some universal constant
for some universal constant  .
.
The proof of Theorem 3.2 will be presented in § 5.
The following corollary is an immediate consequence of Theorem 3.2.
Corollary 3.3. Assume the conditions of Theorem 3.2. Then there exists a Lipschitz continuous map

with the following properties:
- (i)
- (ii)for every


This map  plays a crucial role in the definition of our determining form. To be more specific, let
plays a crucial role in the definition of our determining form. To be more specific, let  be a steady state of the NSE (2.2). Our determining form is the equation
be a steady state of the NSE (2.2). Our determining form is the equation
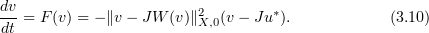
The precise properties of (3.10) are stated in Theorem 3.5, below. But first we need the following result.
Proposition 3.4. Suppose that 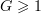 . Then for every
. Then for every 
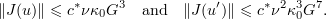
Consequently,
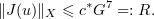
Proof. Since 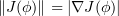 , we apply (3.2) and use the fact that by (3.9) we have
, we apply (3.2) and use the fact that by (3.9) we have 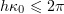 , together with Proposition 2.3. □
, together with Proposition 2.3. □
Theorem 3.5. Let  and suppose that the conditions of Theorem 3.2 hold for
and suppose that the conditions of Theorem 3.2 hold for  , where
, where  as in Proposition 3.4. Then the following hold.
as in Proposition 3.4. Then the following hold.
- (i)
- (ii)
- (iii)
- (iv)
Proof. To show short-time existence it is sufficient to show that the vector field (3.10) is Lipschitz. Let  , where
, where  . Since
. Since
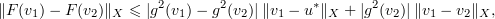
it suffices to show that the map 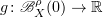 is Lipschitz. Note that for
is Lipschitz. Note that for  we have
we have
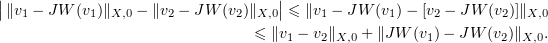
Next, by (3.2) and the triangle inequality,
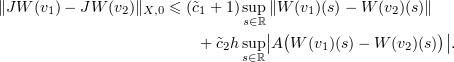
By virtue of Corollary 3.3 and the fact that  ,
,
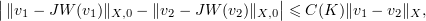
where  satisfies (3.7) with
satisfies (3.7) with  . This completes the proof of
. This completes the proof of
By Proposition 3.4,  . Thus, we have short-time existence of a solution of (3.10) with initial data in
. Thus, we have short-time existence of a solution of (3.10) with initial data in  . The proof of
. The proof of 
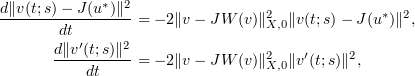
where  . This property implies that the ball
. This property implies that the ball  is forward invariant for all
is forward invariant for all 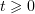 , which simultaneously proves
, which simultaneously proves
To prove part  are either
are either 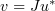 or
or  such that
such that  . In the first case
. In the first case  , since
, since  is a steady state of the NSE (2.2). In the second case we have
is a steady state of the NSE (2.2). In the second case we have  , that is,
, that is,  for all
for all  , where
, where  is a solution of (3.6). In this case it follows from (3.6) that
is a solution of (3.6). In this case it follows from (3.6) that 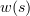 is a bounded solution of the NSE (2.2). Therefore, one concludes from (2.6) that
is a bounded solution of the NSE (2.2). Therefore, one concludes from (2.6) that  is a trajectory in the global attractor
is a trajectory in the global attractor 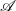 of the NSE. Conversely, since
of the NSE. Conversely, since  , it follows from Proposition 3.4 that
, it follows from Proposition 3.4 that  . Thus, for every trajectory
. Thus, for every trajectory  it follows from Proposition 3.1 and (3.6) that
it follows from Proposition 3.1 and (3.6) that  for all
for all  . In particular,
. In particular, 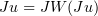 , and consequently
, and consequently  is a steady state of (3.10) in
is a steady state of (3.10) in  . □
. □
4. Proof of Proposition 3.1
In view of (2.2) and (3.3) the difference  satisfies
satisfies
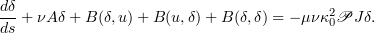
Suppose that  for some
for some  . Since
. Since  is a continuous function with values in
is a continuous function with values in  , there is a maximal interval
, there is a maximal interval 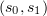 containing
containing  such that
such that  for all
for all  . Taking the scalar product with
. Taking the scalar product with  and using (2.8), (2.9), (2.18), we find that for all
and using (2.8), (2.9), (2.18), we find that for all 
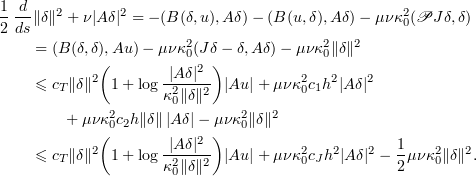
By (3.5) we have

that is,
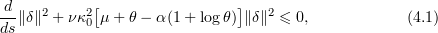
where
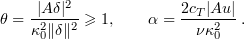
We now seek a lower estimate of  for
for  . Note that
. Note that

and that  is decreasing for
is decreasing for  and increasing for
and increasing for 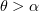 . Thus,
. Thus,
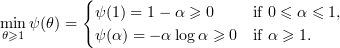
Now note that for ![$\alpha \in (0,1]$](https://content.cld.iop.org/journals/0036-0279/69/2/359/revision1/rms_69_2_359ieqn243.gif) we have
we have  . Indeed, it is easy to check that
. Indeed, it is easy to check that  satisfies
satisfies 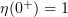 ,
,  , and
, and  . We conclude that
. We conclude that

Applying (4.2) and then (2.22) to (4.1), we find that since  ,
,
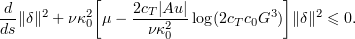
It follows that
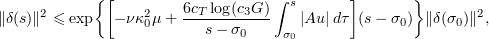
where  and
and  . If
. If  , then
, then  , so we take
, so we take  and conclude that
and conclude that  for
for  . Otherwise it follows from (2.22) that
. Otherwise it follows from (2.22) that
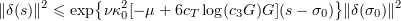
for large enough  . Letting
. Letting  , we find by (3.4) that
, we find by (3.4) that 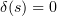 . Since
. Since  is arbitrary,
is arbitrary,  in particular, a contradiction proving the proposition.
in particular, a contradiction proving the proposition.
5. Proof of Theorem 3.2
In this section we give a formal proof of each estimate stated in Theorem 3.2. However, we describe below how to give a rigorous justification for the existence of a solution  of (3.6) which satisfies, together with
of (3.6) which satisfies, together with  , these estimates. First, one considers the following Galerkin approximation system for (3.6):
, these estimates. First, one considers the following Galerkin approximation system for (3.6):
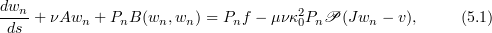
where  is the orthogonal projection from
is the orthogonal projection from  onto
onto 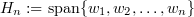 , the space of the first
, the space of the first  eigenfunctions of the Stokes operator
eigenfunctions of the Stokes operator  .
.
Proposition 5.1. Equation (5.1) has a solution  for all
for all  which satisfies, together with
which satisfies, together with  , all the estimates in Theorem 3.2.
, all the estimates in Theorem 3.2.
Proof. For  we supplement (5.1) with an initial value
we supplement (5.1) with an initial value  in order to obtain a finite system of ODEs with a quadratic polynomial non-linearity. Therefore, (5.1) with this initial data possesses a unique solution
in order to obtain a finite system of ODEs with a quadratic polynomial non-linearity. Therefore, (5.1) with this initial data possesses a unique solution  on a small time interval symmetric about the initial time
on a small time interval symmetric about the initial time  . Furthermore, on this small interval
. Furthermore, on this small interval 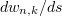 is the unique solution of the Cauchy problem
is the unique solution of the Cauchy problem
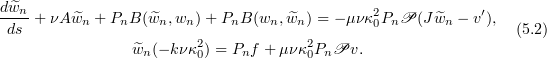
For the interval  one can follow the same steps as used below in establishing estimates of
one can follow the same steps as used below in establishing estimates of  to show that the same estimates are also valid for
to show that the same estimates are also valid for  when
when  . Thus,
. Thus,  remains bounded for
remains bounded for  , and as a result it solves (5.1) for
, and as a result it solves (5.1) for  . And since
. And since  is finite and independent of
is finite and independent of  , one can show, by following steps similar to those used below for estimating
, one can show, by following steps similar to those used below for estimating  and
and  , that
, that  is bounded uniformly independent of
is bounded uniformly independent of  for all
for all 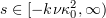 .
.
Now let  . Then by employing the Arzelà–Ascoli compactness theorem one can extract a subsequence
. Then by employing the Arzelà–Ascoli compactness theorem one can extract a subsequence  of
of  which converges as
which converges as  to a solution
to a solution  of (5.1) on the interval
of (5.1) on the interval ![$[-j\nu \kappa_0^2,j\nu \kappa_0^2]$](https://content.cld.iop.org/journals/0036-0279/69/2/359/revision1/rms_69_2_359ieqn296.gif) . Moreover,
. Moreover,  and
and  satisfy the estimates in Theorem 3.2 for all
satisfy the estimates in Theorem 3.2 for all ![$s \in [-j\nu \kappa_0^2,j\nu \kappa_0^2]$](https://content.cld.iop.org/journals/0036-0279/69/2/359/revision1/rms_69_2_359ieqn299.gif) . Now by the Cantor diagonal process one can show that
. Now by the Cantor diagonal process one can show that  converges to
converges to 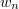 as
as  , and that
, and that  has the properties stated in the proposition. □
has the properties stated in the proposition. □
We continue with our proof of the theorem. Based on Proposition 5.1, we use the Aubin compactness theorem (see, for instance, [6] or [22]) to show that for every  there exists a subsequence
there exists a subsequence  of
of  which converges to
which converges to  in the relevant spaces on the interval
in the relevant spaces on the interval ![$[-\nu \kappa_0 m, \nu \kappa_0 m]$](https://content.cld.iop.org/journals/0036-0279/69/2/359/revision1/rms_69_2_359ieqn308.gif) as
as  . Moreover, by passing to the limit and following arguments similar to those for the 2D NSE, one infers that
. Moreover, by passing to the limit and following arguments similar to those for the 2D NSE, one infers that  is a solution of (3.6) on the interval
is a solution of (3.6) on the interval ![$[-\nu \kappa_0 m, \nu \kappa_0 m]$](https://content.cld.iop.org/journals/0036-0279/69/2/359/revision1/rms_69_2_359ieqn311.gif) , and in addition,
, and in addition,  and
and  satisfy the estimates in Theorem 3.2 on the interval
satisfy the estimates in Theorem 3.2 on the interval ![$[-\nu \kappa_0 m, \nu \kappa_0 m]$](https://content.cld.iop.org/journals/0036-0279/69/2/359/revision1/rms_69_2_359ieqn314.gif) . Now we again use the Cantor diagonal process to show that the diagonal subsequence
. Now we again use the Cantor diagonal process to show that the diagonal subsequence  converges as
converges as 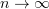 to a solution
to a solution  of (3.6). Moreover,
of (3.6). Moreover,  and
and  satisfy the estimates in Theorem 3.2 for all
satisfy the estimates in Theorem 3.2 for all  . This in turn concludes the formal justification of the estimates that will be established below.
. This in turn concludes the formal justification of the estimates that will be established below.
5.1. Bound for  .
.
Taking the inner product of (3.6) with  and using (2.8), we have
and using (2.8), we have
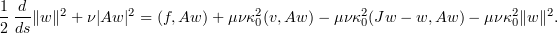
From (3.1) we get that
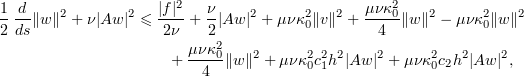
and thus
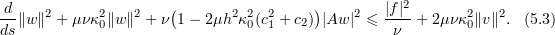
Therefore, if we assume that  is small enough that
is small enough that

then by Gronwall's inequality and the assumption that  is bounded we have the estimate
is bounded we have the estimate
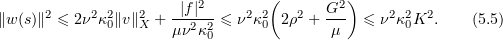
Next, we consider the evolution equation for  :
:
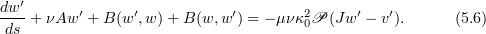
5.2. Bound for  .
.
Taking the inner product of (5.6) with  and using (2.9) and (3.1) (after following steps similar to those above), one obtains
and using (2.9) and (3.1) (after following steps similar to those above), one obtains
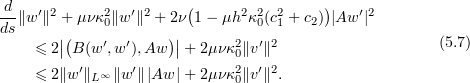
Now by applying (2.28) to  we get that
we get that
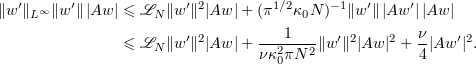
Hence by (5.4)
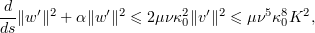
where
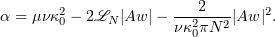
We get from (5.3) and (5.4) that
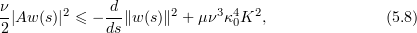
and in view of (5.5) integration gives us
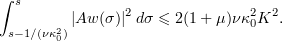
Applying the Cauchy–Schwarz inequality, we have
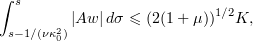
and hence
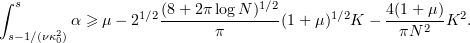
We want to make sure that
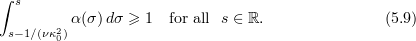
If we choose  , then (5.9) follows from requiring that
, then (5.9) follows from requiring that
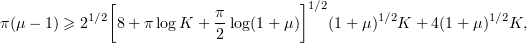
which automatically holds if
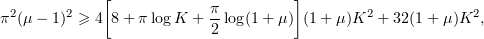
which is equivalent to
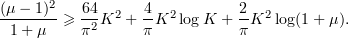
Since
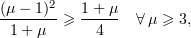
it suffices that
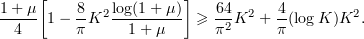
Since  ,
, 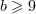 , it follows that
, it follows that  , and we set
, and we set  and
and  , so that if
, so that if
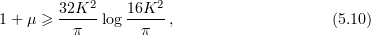
then it suffices that
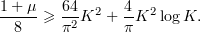
Thus, to ensure that (5.9) holds, we take

By a similar calculation, again taking  , we get that for
, we get that for 
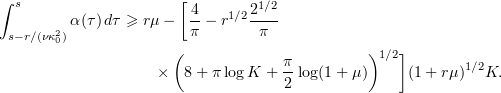
Therefore, if

then for some 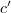 we have
we have
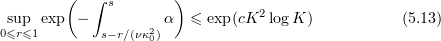
for some absolute constant  . Ultimately, we will choose
. Ultimately, we will choose  so that (5.12) is compatible with (5.11) (see (5.20)).
so that (5.12) is compatible with (5.11) (see (5.20)).
Lemma 5.2. Let  be a constant and let
be a constant and let  be an absolutely continuous bounded function satisfying the inequality
be an absolutely continuous bounded function satisfying the inequality  for all
for all  . Suppose also that
. Suppose also that 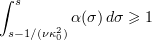 for all
for all  . Then
. Then
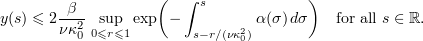
Proof. Note that since  , we have
, we have  . Multiplying
. Multiplying  by the integrating factor
by the integrating factor  and integrating from
and integrating from  to
to  , we find that
, we find that

From Lemma 5.2, (5.9), and (5.13),
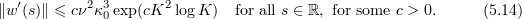
5.3. Bounds for  and
and  .
.
From (5.8) we get that
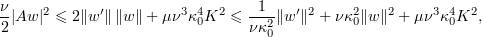
and hence by (5.14) and (5.5) we have
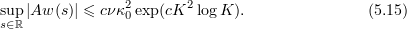
From (3.6) we find that
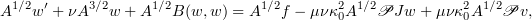
and thus by (2.24)
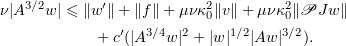
Since  , we get from (3.2) that
, we get from (3.2) that
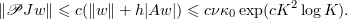
Thus, by (5.12) and (5.15) we have
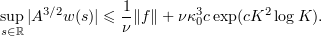
5.4. Bound for  .
.
Taking the inner product of  with the equation
with the equation
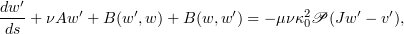
we get that
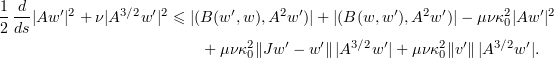
We bound the first non-linear term using (2.15) and (2.25) to get that
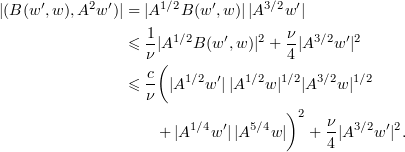
For the second non-linear term we integrate by parts, using the fact that  under periodic boundary conditions, so that by (2.7), (2.8), (2.13), (2.11), and (2.15) we have
under periodic boundary conditions, so that by (2.7), (2.8), (2.13), (2.11), and (2.15) we have
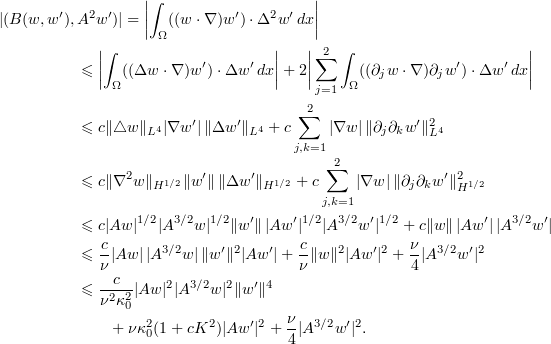
Using (2.25), (3.2), and the bounds for  and
and  , we now obtain by Gronwall's inequality the uniform bound
, we now obtain by Gronwall's inequality the uniform bound
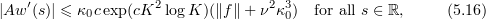
provided that 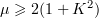 (which, in turn follows from (5.11)).
(which, in turn follows from (5.11)).
5.5. Lipschitz property of  and
and  in the
in the  norm.
norm.
In this section we show that the bounded solutions of (3.6) are unique and depend continuously on the input trajectory  , in a sense that will be specified below. In particular, these properties are instrumental for introducing a well-defined map
, in a sense that will be specified below. In particular, these properties are instrumental for introducing a well-defined map  from the space
from the space  to a space of trajectories, which is defined by
to a space of trajectories, which is defined by  for all
for all  .
.
To obtain these properties we consider the difference  between two trajectories
between two trajectories  and
and  and establish estimates for
and establish estimates for  and
and  similar to those for
similar to those for  and
and  . Indeed, by linearity the only complication is in the non-linear term. Let
. Indeed, by linearity the only complication is in the non-linear term. Let  , and
, and  . Then
. Then
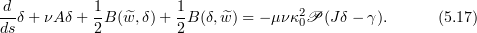
5.6. Bound for  .
.
Taking the scalar product of (5.17) with  , we find as in § 5.1 that
, we find as in § 5.1 that
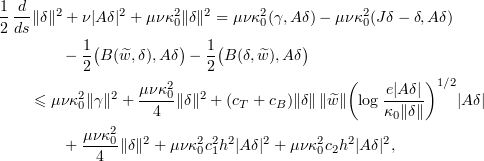
where for the non-linear terms we used (2.18) and (2.19). Applying Young's inequality to the contribution from the non-linear terms, we find that if (3.5) holds, then by (5.5)
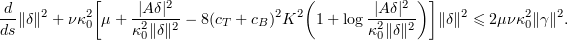
At this point we can use (4.2) with  and
and  to obtain
to obtain
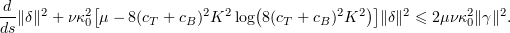
Therefore, if
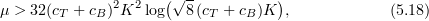
then

To ensure compatibility of (5.11) and (5.18) we take, as in (3.8),
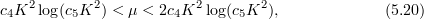
where  and
and  .
.
5.7. Bound for  .
.
The equation for  is
is
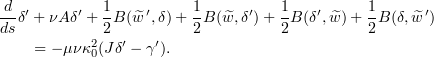
Taking the scalar product with  , we get that
, we get that
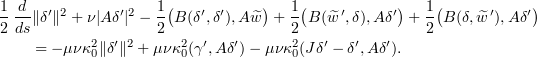
Note that the difference from (5.7) (when one changes  to
to  and
and  to
to  ) is in the addition of the two terms
) is in the addition of the two terms  and
and  , so that if we can show that they are bounded by a constant multiple of
, so that if we can show that they are bounded by a constant multiple of  , then we obtain the Lipschitz property of
, then we obtain the Lipschitz property of  by using the same methods as in § 5.2.
by using the same methods as in § 5.2.
We begin with
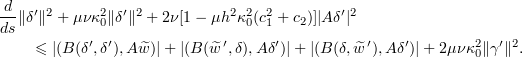
Consequently, we have
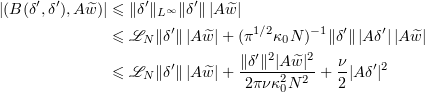
and (by (2.16))
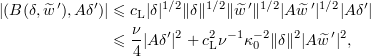
along with (by (2.17))
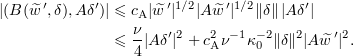
Thus,
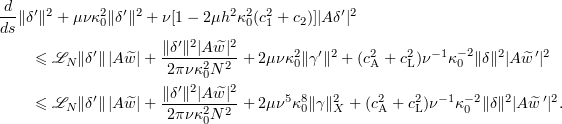
By (3.5) we can drop the term containing  . Then applying (5.16) to
. Then applying (5.16) to  and using (5.19), we have
and using (5.19), we have

where
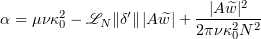
and
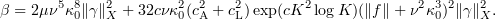
Proceeding as in § 5.2, we get that
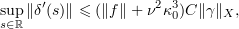
where  for some universal constant
for some universal constant  . Note that once again (5.9) suffices to ensure that (5.12) holds, so there is no need to modify the range for
. Note that once again (5.9) suffices to ensure that (5.12) holds, so there is no need to modify the range for 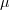 in (5.12).
in (5.12).