Export citation and abstract BibTeX RIS
We consider meromorphic linear ordinary differential operators acting on functions of a real variable  and having the form
and having the form 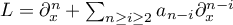 with coefficients meromorphic near the axis
with coefficients meromorphic near the axis 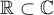 . Such an operator is said to be spectrally meromorphic (or s-meromorphic) at a pole
. Such an operator is said to be spectrally meromorphic (or s-meromorphic) at a pole 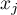 if all the solutions of the equation
if all the solutions of the equation 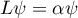 are meromorphic near
are meromorphic near 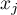 for all
for all 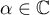 . We shall study operators that are s-meromorphic at all their poles
. We shall study operators that are s-meromorphic at all their poles  .
.
We introduce the necessary function spaces. Given a set of vector subspaces 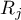 of the form
of the form 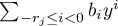 in the space of all Laurent polynomials, we define the space
in the space of all Laurent polynomials, we define the space  of all functions that are meromorphic near the axis
of all functions that are meromorphic near the axis  , with possible poles at a fixed discrete set of points
, with possible poles at a fixed discrete set of points  and with the principal parts of their Laurent expansions with respect to
and with the principal parts of their Laurent expansions with respect to 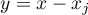 belonging to the fixed subspaces
belonging to the fixed subspaces 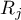 . The only restrictions on the positive Laurent coefficients at the poles
. The only restrictions on the positive Laurent coefficients at the poles 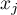 follow from the requirement that the products of functions in
follow from the requirement that the products of functions in  do not have terms of the form
do not have terms of the form  .
.
Lemma 1. The formula 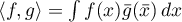 gives a well-defined scalar product for all compactly supported functions
gives a well-defined scalar product for all compactly supported functions 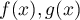 ,
,  , in the space
, in the space  , where the integral is taken over the axis
, where the integral is taken over the axis  outside a neighbourhood of the singularities and over a contour going around the singular points and close to them. This scalar product is indefinite, and each singular point
outside a neighbourhood of the singularities and over a contour going around the singular points and close to them. This scalar product is indefinite, and each singular point 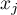 gives
gives  negative squares (independently of the other points
negative squares (independently of the other points  ), where
), where  is the dimension of the subspace
is the dimension of the subspace 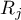 of the Laurent principal parts near
of the Laurent principal parts near 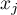 .
.
The proof follows easily from the fact that, by the definition of the space  , a product of functions does not contain powers
, a product of functions does not contain powers  near any pole. According to the BChK construction (Burchnall–Chandy–Krichever [1]), a Riemann surface
near any pole. According to the BChK construction (Burchnall–Chandy–Krichever [1]), a Riemann surface  endowed with a distinguished point
endowed with a distinguished point  , a local parameter
, a local parameter  , a divisor
, a divisor 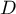 of degree
of degree  (the genus), and a meromorphic function
(the genus), and a meromorphic function 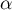 with a pole only at
with a pole only at  of order
of order  determines a
determines a  th-order ordinary differential operator
th-order ordinary differential operator 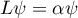 which is algebraic of rank 1. This operator is easily seen to be s-meromorphic. It is formally self-adjoint (symmetric) if the following condition
which is algebraic of rank 1. This operator is easily seen to be s-meromorphic. It is formally self-adjoint (symmetric) if the following condition 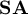 holds: we are given an anti-involution
holds: we are given an anti-involution  with
with  such that
such that 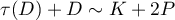 ,
,  .
.
The singularities of the operator  determine a class of functions
determine a class of functions  (see above). In the periodic case we construct the space
(see above). In the periodic case we construct the space 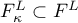 of functions with
of functions with  ,
,  . The number of negative squares in the spaces
. The number of negative squares in the spaces 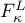 is finite. We recall that the differential of the quasi-momentum is a meromorphic differential
is finite. We recall that the differential of the quasi-momentum is a meromorphic differential  having only a second-order pole at
having only a second-order pole at  with
with  and such that the integrals
and such that the integrals 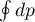 over all cycles are purely real. Since
over all cycles are purely real. Since  , we choose
, we choose  to be a single-valued real function with
to be a single-valued real function with  . The level
. The level  is called the canonical contour
is called the canonical contour  .
.
The projection 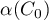 of the contour
of the contour  on the complex plane
on the complex plane  coincides with the spectrum of
coincides with the spectrum of  on the whole axis
on the whole axis  in the space
in the space 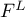 .
.
Theorem 2. The scalar product in the space  for an algebraic operator
for an algebraic operator  of rank 1 satisfying the condition
of rank 1 satisfying the condition 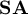 is well defined and indefinite. The operator
is well defined and indefinite. The operator  is self-adjoint with respect to this scalar product (see above). Its spectrum coincides with the set
is self-adjoint with respect to this scalar product (see above). Its spectrum coincides with the set 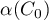 , where
, where  is the canonical contour. The scalar product is given by the integral over the contour
is the canonical contour. The scalar product is given by the integral over the contour  with the spectral measure
with the spectral measure 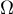 . If the basis of eigenfunctions on
. If the basis of eigenfunctions on  is complete in the space
is complete in the space 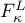 , then the number of negative squares for the scalar product in the spaces
, then the number of negative squares for the scalar product in the spaces 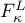 is determined by the sign of the spectral measure
is determined by the sign of the spectral measure 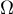 at the corresponding points of
at the corresponding points of  and is an integral of the Gelfand–Dickey systems
and is an integral of the Gelfand–Dickey systems ![$\dot L=[L,A]$](https://content.cld.iop.org/journals/0036-0279/69/5/924/revision1/RMS_69_5_924ieqn50.gif) .
.
To prove the theorem, we consider the Baker–Akhiezer function  (near
(near  ) with pole divisor
) with pole divisor 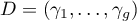 and the dual 1-form
and the dual 1-form  (near
(near  ) with zeros
) with zeros 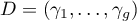 . In the language of scalar Baker– Akhiezer functions we have
. In the language of scalar Baker– Akhiezer functions we have  , where
, where  near
near  , with zeros
, with zeros 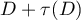 ,
, 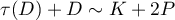 . Here
. Here  is the canonical divisor of differential forms and
is the canonical divisor of differential forms and 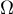 is the spectral measure on the contour
is the spectral measure on the contour  . We have
. We have  , where
, where  is the conjugate of
is the conjugate of  . This fact has perhaps not been mentioned explicitly in the literature. A Cauchy-type kernel on
. This fact has perhaps not been mentioned explicitly in the literature. A Cauchy-type kernel on  was studied in [2]:
was studied in [2]:  near the diagonal
near the diagonal 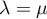 ,
,  as
as  , and
, and 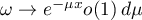 as
as  . It was found that
. It was found that  . This equality plays a key role here. It follows that the residue with respect to
. This equality plays a key role here. It follows that the residue with respect to 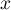 is equal to zero for any product of eigenfunctions of the self-adjoint operator
is equal to zero for any product of eigenfunctions of the self-adjoint operator  near the singularity. Hence the scalar product (see above) is well defined. For any given
near the singularity. Hence the scalar product (see above) is well defined. For any given  , the number of negative squares is an invariant of the Riemann surface, which is preserved under evolution in time: the equation
, the number of negative squares is an invariant of the Riemann surface, which is preserved under evolution in time: the equation  on the contour
on the contour  gives a discrete set of points
gives a discrete set of points 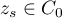 . The number of points at which the quantity
. The number of points at which the quantity 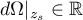 is negative, is finite and gives the number of negative squares for the scalar product in
is negative, is finite and gives the number of negative squares for the scalar product in 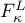 . The whole space
. The whole space  is a direct integral of the spaces
is a direct integral of the spaces 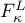 .
.
Example. [3] For  we have
we have 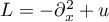 . Suppose that
. Suppose that  . For
. For  -meromorphy, the regular part of the potential must have zero odd derivatives at
-meromorphy, the regular part of the potential must have zero odd derivatives at 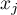 up to and including order
up to and including order  . All the spaces
. All the spaces 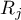 are of the form
are of the form  for even
for even  , or
, or 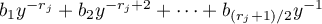 for odd
for odd  . Each pole gives
. Each pole gives ![$[(r_j+1)/2]$](https://content.cld.iop.org/journals/0036-0279/69/5/924/revision1/RMS_69_5_924ieqn81.gif) negative squares. The positive terms of the Laurent expansion of functions
negative squares. The positive terms of the Laurent expansion of functions 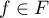 at the points
at the points 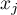 have zero coefficients of the odd powers
have zero coefficients of the odd powers  with
with 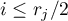 in the first case, and of the even powers
in the first case, and of the even powers  with
with  in the second case. One of the finite components of the spectrum
in the second case. One of the finite components of the spectrum 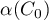 is complex already for the genus
is complex already for the genus  and the real elliptic potential corresponding to the rhombic lattice. The completeness of the eigenfunctions is proved in [3]. Hence the number of negative squares is preserved under the action of the KdV and the higher KdVs.
and the real elliptic potential corresponding to the rhombic lattice. The completeness of the eigenfunctions is proved in [3]. Hence the number of negative squares is preserved under the action of the KdV and the higher KdVs.
The following are to be proved. 1. If an operator is  -meromorphic, then so is its conjugate operator. 2. All the singularities
-meromorphic, then so is its conjugate operator. 2. All the singularities 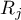 of
of  -meromorphic operators are realized by algebraic ones. Their classification is an open problem. 3. The completeness theorem for symmetric algebraic operators.
-meromorphic operators are realized by algebraic ones. Their classification is an open problem. 3. The completeness theorem for symmetric algebraic operators.



