Export citation and abstract BibTeX RIS
We consider the problem of solutions of the equation
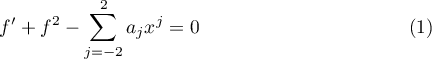
that are rational in the variable 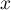 . It is easy to see that such a solution must have the form
. It is easy to see that such a solution must have the form

Proposition 1. A function (2) solves (1) if and only if

and
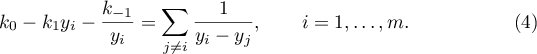
The coefficients  in (1) are defined up to the scaling
in (1) are defined up to the scaling 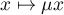 ,
, 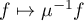 . For definiteness, in what follows we will assume that
. For definiteness, in what follows we will assume that 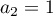 , so that
, so that  . It is easy to see that, as
. It is easy to see that, as  , a rational solution of (1) has an expansion
, a rational solution of (1) has an expansion
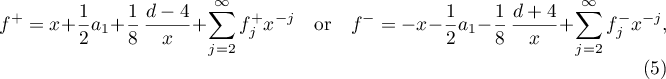
where 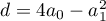 . The properties of formal solutions of the form (5) and questions related to their convergence were considered in [1].
. The properties of formal solutions of the form (5) and questions related to their convergence were considered in [1].
Example 1. Assume that the potential in the Riccati equation is an even function (so that  ) and a rational solution is an odd function. Then a solution of the form
) and a rational solution is an odd function. Then a solution of the form

exists if and only if the Riccati equation has the form
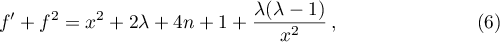
and the polynomial 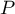 solves the linear equation
solves the linear equation 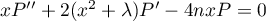 . From it we find that
. From it we find that  and
and  , where
, where 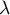 is an arbitrary parameter.
is an arbitrary parameter.
For each positive integer 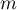 the equation
the equation
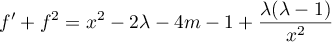
has the solution

Here 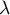 is an arbitrary parameter. If
is an arbitrary parameter. If 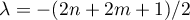 , then (6) has two rational solutions,
, then (6) has two rational solutions,  and
and  .
.
Theorem. Assume that (1) with  has two rational solutions,
has two rational solutions,
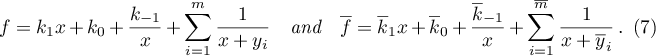
Then
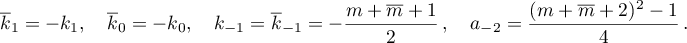
Corollary. Equation (1) with  has at most two rational solutions.
has at most two rational solutions.
Taking 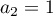 , we can assume without loss of generality that
, we can assume without loss of generality that  and
and  . Then for fixed
. Then for fixed 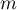 and
and  and for the
and for the 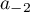 ,
,  ,
,  ,
,  , and
, and 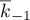 defined above, the relations (3) and (4) take us to a system of
defined above, the relations (3) and (4) take us to a system of  equations with respect to the
equations with respect to the  unknowns
unknowns 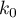 ,
, 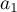 ,
,  ,
,  ,
, 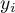 , and
, and 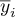 . This system can easily be solved for small
. This system can easily be solved for small 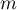 and
and  . In particular, the case when
. In particular, the case when  is described in Example 1.
is described in Example 1.
Example 2. For  and
and  we obtain the Riccati equation
we obtain the Riccati equation

which has the two rational solutions

It is clear that a rational solution 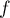 of a Riccati equation defines the solution
of a Riccati equation defines the solution  of the corresponding linear Schrödinger equation.
of the corresponding linear Schrödinger equation.
An algorithm for finding elementary solutions of a second-order linear equation with rational coefficients was put forward in [2]. In our case this algorithm is based on the observation that (for fixed numerical values of the coefficients  in (1)) the formulae (3) determine at most four possible values of
in (1)) the formulae (3) determine at most four possible values of 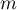 , each of which must be investigated separately. The two rational solutions
, each of which must be investigated separately. The two rational solutions  and
and  yield [3] the solution
yield [3] the solution 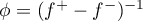 of a third-order linear equation which is well known in soliton theory.
of a third-order linear equation which is well known in soliton theory.
The authors acknowledge useful discussions with V. G. Marikhin and are grateful to the participants of the seminar on mathematical physics at the Landau Institute for Theoretical Physics for their interest in this work.



