Export citation and abstract BibTeX RIS
One important indicator of the adequacy of a numerical solution of an autonomous system of differential equations is the topological conjugacy of the discrete model obtained to the time-one shift map of the original flow. The most significant results in this direction have been obtained for structurally stable flows. In particular, it was shown in [1] and [2] that the Runge–Kutta discretization of a Morse–Smale flow (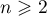 ) without periodic trajectories on the
) without periodic trajectories on the 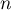 -disk is topologically conjugate to the time-one shift (for a sufficiently small step size). In this connection the question, going back to Palis [3], of necessary and sufficient conditions for embedding a Morse–Smale diffeomorphism in a topological flow arises naturally.
-disk is topologically conjugate to the time-one shift (for a sufficiently small step size). In this connection the question, going back to Palis [3], of necessary and sufficient conditions for embedding a Morse–Smale diffeomorphism in a topological flow arises naturally.
Recall that a diffeomorphism  on a closed manifold
on a closed manifold 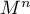 is called a Morse–Smale diffeomorphism if its non-wandering set
is called a Morse–Smale diffeomorphism if its non-wandering set 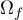 is finite and consists of hyperbolic periodic points, and for any two points
is finite and consists of hyperbolic periodic points, and for any two points 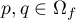 the intersection of the stable manifold
the intersection of the stable manifold 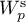 of
of 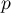 and the unstable manifold
and the unstable manifold  of
of  is transversal. In [3] the following necessary conditions for embedding a Morse–Smale diffeomorphism
is transversal. In [3] the following necessary conditions for embedding a Morse–Smale diffeomorphism  in a topological flow were stated, and we call them the Palis conditions: 1) the non-wandering set
in a topological flow were stated, and we call them the Palis conditions: 1) the non-wandering set 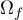 coincides with the set of fixed points; 2) the restriction of the diffeomorphism
coincides with the set of fixed points; 2) the restriction of the diffeomorphism  to each invariant manifold of each fixed point
to each invariant manifold of each fixed point 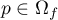 preserves its orientation; 3) if for any distinct saddle points
preserves its orientation; 3) if for any distinct saddle points 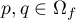 the intersection
the intersection 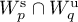 is non-empty, then it contains no compact connected components.
is non-empty, then it contains no compact connected components.
According to [3], in the case when  these conditions are not only necessary but also sufficient. In [4] examples of Morse–Smale diffeomorphisms on the three-dimensional sphere were constructed that satisfy the Palis conditions but do not embed in topological flows, and also necessary and sufficient conditions were obtained for embedding a three-dimensional Morse–Smale diffeomorphism in a topological flow. An additional obstruction to embedding such diffeomorphisms in topological flows is connected with the possibility of a non- trivial embedding of the separatrices of saddle points in the ambient manifold. In the present paper we show that for the class
these conditions are not only necessary but also sufficient. In [4] examples of Morse–Smale diffeomorphisms on the three-dimensional sphere were constructed that satisfy the Palis conditions but do not embed in topological flows, and also necessary and sufficient conditions were obtained for embedding a three-dimensional Morse–Smale diffeomorphism in a topological flow. An additional obstruction to embedding such diffeomorphisms in topological flows is connected with the possibility of a non- trivial embedding of the separatrices of saddle points in the ambient manifold. In the present paper we show that for the class  of Morse–Smale diffeomorphisms without heteroclinic intersections defined on the sphere
of Morse–Smale diffeomorphisms without heteroclinic intersections defined on the sphere  of dimension
of dimension 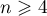 and satisfying the Palis conditions no such obstruction exists and the following theorem holds.
and satisfying the Palis conditions no such obstruction exists and the following theorem holds.
Theorem 1. Any diffeomorphism 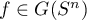 ,
, 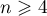 , is embedded in a topological flow.
, is embedded in a topological flow.
The main tool of the proof is the scheme of a diffeomorphism, defined below. Let 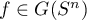 . It follows from the connection between the dynamics of the diffeomorphism
. It follows from the connection between the dynamics of the diffeomorphism  and the homologies of the sphere
and the homologies of the sphere  that for any saddle point of
that for any saddle point of  either the stable or the unstable manifold has dimension 1. Denote by
either the stable or the unstable manifold has dimension 1. Denote by 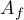 and
and 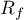 the unions of the closures of the unstable and the stable one-dimensional invariant manifolds of the saddle points, respectively; if
the unions of the closures of the unstable and the stable one-dimensional invariant manifolds of the saddle points, respectively; if  has no saddle points with one-dimension unstable (stable) manifolds, then it has a unique sink (source) fixed point, which we also denote by
has no saddle points with one-dimension unstable (stable) manifolds, then it has a unique sink (source) fixed point, which we also denote by 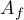 (
(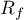 ). Let
). Let  . According to [5], the sets
. According to [5], the sets 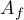 ,
, 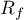 , and
, and 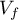 are connected, and
are connected, and 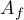 is an attractor,
is an attractor, 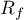 is a repeller, and
is a repeller, and 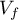 consists of the wandering points of
consists of the wandering points of  going from
going from 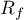 to
to 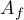 and contains all the saddle separatrices of codimension 1.
and contains all the saddle separatrices of codimension 1.
Denote by 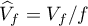 the orbit space of the
the orbit space of the  -action on
-action on 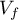 , by
, by 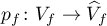 the natural projection, and by
the natural projection, and by  the epimorphism induced by
the epimorphism induced by 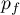 . Let
. Let 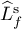 and
and 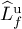 denote the unions of the projections onto
denote the unions of the projections onto  of all the stable and unstable separatrices of the saddle points, respectively. The set
of all the stable and unstable separatrices of the saddle points, respectively. The set  is called the scheme of the diffeomorphism
is called the scheme of the diffeomorphism 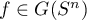 . The schemes
. The schemes 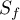 and
and 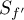 of diffeomorphisms
of diffeomorphisms 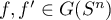 are said to be equivalent if there exists a homeomorphism
are said to be equivalent if there exists a homeomorphism 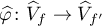 with the following properties: 1)
with the following properties: 1) 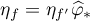 ; 2)
; 2) 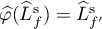 and
and 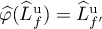 .
.
According to [6], the scheme is a complete topological invariant for diffeomorphisms in  . The key and most non-trivial point for embedding a diffeomorphism
. The key and most non-trivial point for embedding a diffeomorphism 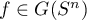 ,
, 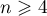 , in a flow is the equivalence of the scheme
, in a flow is the equivalence of the scheme 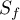 to the following standard object. Let
to the following standard object. Let 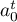 be a flow on
be a flow on 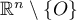 defined by the formula
defined by the formula  , let
, let  be the time-one shift along trajectories of
be the time-one shift along trajectories of 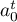 , let
, let 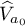 be the orbit space of the
be the orbit space of the  -action on
-action on 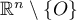 (which is diffeomorphic to
(which is diffeomorphic to 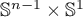 ), and let
), and let 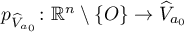 be the natural projection. On the unit sphere
be the natural projection. On the unit sphere 
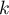 we choose smooth pairwise disjoint
we choose smooth pairwise disjoint 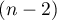 -spheres
-spheres 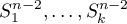 . Let
. Let 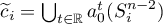 and
and 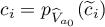 . We choose an integer
. We choose an integer ![$m\in[0,k]$](https://content.cld.iop.org/journals/0036-0279/71/6/1146/revision1/RMS_71_6_1146ieqn51.gif) and let
and let 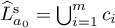 and
and 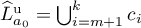 . The set
. The set  is called the standard scheme.
is called the standard scheme.
Lemma. The scheme 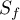 of a diffeomorphism
of a diffeomorphism 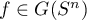 ,
, 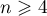 , is equivalent to the standard scheme for some
, is equivalent to the standard scheme for some 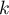 and
and 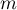 .
.
This lemma allows one to use the method in [4] to construct a flow 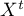 whose time-one shift has a scheme equivalent to
whose time-one shift has a scheme equivalent to 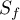 . Since the scheme is a complete invariant, there exists a homeomorphism
. Since the scheme is a complete invariant, there exists a homeomorphism 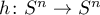 such that
such that 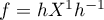 . Hence
. Hence  is embedded in the flow
is embedded in the flow 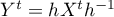 .
.



