To the memory of Èmmanuil Èl'evich Shnol'

This paper is dedicated to the life and deeds of Èmmanuil Èl'evich Shnol', doctor of the physical and mathematical sciences and professor. He was a brilliant and multiply talented person, who left a deep impression in the hearts of those who were fortunate enough to know him. A remarkable mathematician, both pure and applied, Shnol' in no way belonged to the number of narrow specialists. His interests were not confined to any particular area of mathematics, nor even to mathematics as a whole. His nature was that of a natural scientist in the broadest sense.

Zoom In Zoom Out Reset image size

È. È. Shnol' was born on 26 August 1928. His father Èli Gershevich Shnol' was an encyclopaedically educated person, an expert in languages, a philosopher of religion, whose pedagogical and enlightening activities were ended in 1933 by arrest and a labour camp, from which he emerged hopelessly ill and died in 1940. The mother Faina Yakovlevna Yudovich, a psychologist and a pedagogue-philologist, brought up three sons. They all became known researchers, doctors of different sciences: Èmmanuil in mathematics, Simon in biology, and Yakov in geology. The memory of their father and his guidance (`letter to the eldest son') played a large role in the lives of the sons.

Shnol's innate mathematical talent was evident from his early years. During World War II, while in evacuation, he finished secondary school ahead of schedule, and in 1943 he enrolled at the age of 15 in the Faculty of Mechanics and Mathematics at Moscow State University. During his student years he participated in the seminars of I. M. Gelfand and G. E. Shilov, studying valuation rings (see the later publications [1] and [2]) and thinking about Hilbert's 5th problem.

In 1948 Gelfand invited his students Shnol' and A. M. Molchanov to begin graduate studies under his supervision at the Steklov Mathematical Institute, to join the group of calculators on the basis of which the (Keldysh) Institute of Applied Mathematics of the USSR Academy of Sciences was subsequently created. Shnol' successfully passed the entrance examinations for graduate studies, but his biography turned out to be an obstacle, and during the next four years he served in the army as a conscript. Under the austere army conditions of the first post-war years he found the strength to continue studying mathematics, largely due to the support of his closest friend Molchanov, who sent him mathematics books. Here he carried out his best (in his own judgement) mathematical work, devoted to the theory of spectra of Schrödinger operators, which became the basis for his Ph.D. dissertation. On completing his army service, he worked for three years as a mathematics teacher at a Moscow school; and he maintained contacts with his graduates to the last days of his life.

While working at the school, Shnol' made maximum efforts to return to academic research. He published his second paper on the Schrödinger equation [4], which has become classical, and he continued to participate in Gelfand's seminar, where he was given the task of studying and reporting on the recently published solution of Hilbert's 5th problem. He prepared and in 1955 defended his Ph.D. dissertation¹ ``On the behaviour of eigenfunctions of the Schrödinger equation'' at Moscow State University.² In 1956, on the recommendation of K. I. Babenko, who was supported by the director M. V. Keldysh of the Institute of Applied Mathematics, Shnol' was employed at this institute, with which he was to be connected for more than 20 years.

There Shnol' joined a team of researchers who were laying the foundations for modern computational mathematics, an intensively developing scientific discipline which was needed for applications in nuclear and cosmic investigations. Mathematicians of a high level were required, and Shnol' played a valuable role in this team. His research work at the Institute of Applied Mathematics was focused on several directions. First of all were papers in the mainstream of the institute's research areas: the creation of numerical methods for solving two-dimensional gas-dynamics problems. His combination of a purely mathematical view of the problem with the intuition of a calculator enabled him to create methods that were ahead of the requirements of practice at the time. For example, in solving a certain problem in elasticity theory (see [7]), he derived the finite-element method (unfortunately, this was not published but remained classified; a rigorous mathematical justification of the finite-element method began only in the early 1960s, and the first publications appeared in 1963). Shnol' actively participated in the intensive mathematical activities of the institute, and a number of his ideas were subsequently implemented by his colleagues. One such example is the important notion of the spectrum of a family of difference operators, which was born from Shnol's observation on the role of almost eigenfunctions and which made it possible to prove the Babenko–Gelfand stability criterion.³

Apart from Gelfand and Babenko, whom Shnol' regarded as his principal teachers in `pure' and applied mathematics, his formation as a mathematician and a natural scientist was significantly influenced by his contacts with A. S. Kronrod, Shilov, Ya. B. Zel'dovich, D. A. Frank-Kamenetskii, and a number of other prominent scientists.

At the beginning of the 1970s Shnol' entered a new stage of his life, when the other side of his talents, his tremendous creative and pedagogical potentials, developed to the full extent. In these years a new institute was organized due to the efforts of Molchanov and Shnol' (with the support of Keldysh, S. È. Shnol', and G. M. Frank) in the Scientific Centre for Biological Research of the Academy of Sciences in Pushchino:⁴ the Research Computer Centre, or RCC (later renamed the Institute of Mathematical Problems of Biology, or IMPB, of the Russian Academy of Sciences). Together with Molchanov, who was appointed the director, Shnol' embarked on creating this institute, with an academic staff largely recruited from young university graduates. The motivations for organizing the RCC were, on the one hand, an active penetration of mathematical approaches into a number of areas of biology, and on the other hand, a growing demand of these areas for high-performance computer technology (by the standards of that time). Schnol's `zone of responsibility' included both determination of research topics for the institute and professional development of the young people who came to work there, and supervision of the maintenance of computer hardware.

The research areas of the institute were determined to a considerable extent by interaction with the biology laboratories in Pushchino. A substantial role in the organization of this interaction was played by Shnol's contacts with leading Pushchino scientists (E. E. Sel'kov, V. I. Krinskii, F. I. Ataullakhanov, O. B. Ptitsyn, and others) and by the creation of ongoing topical research seminars in which a general understanding would be worked out for some problem in the natural sciences and possible roles of IMPB co-workers in its solution would be determined. The paramount role in coming to such an understanding was played by Schnol's very broad mathematical erudition and his ability to identify the mathematical basis in diverse problems in the natural sciences.

From the very start of his Pushchino period, the matter of utmost importance for Schnol' was training the young research team of the IMPB and establishing connections for them with the `outside world'. This included constant concerns with building up a good scientific library for the institute, starting and supervising a mathematical seminar, and, especially, organizing annual scientific conferences at the RCC/IMPB (1973–1988). These conferences, of which Schnol' was the soul, gathered scientists from many research institutions all over the country annually in the stimulating Pushchino atmosphere, providing an opportunity for regular dialogue between representatives of diverse disciplines. The traditions of the conferences were continued by the annual Pushchino meetings and seminars on differential equations (1986–1990), where, along with theoretical questions, numerical methods were discussed, as well as practical applications of the theory of dynamical systems. It was the influence of Schnol's personality on the style of the Pushchino forums and his erudition in the most diverse range of questions in mathematics and the natural sciences that largely determined the usefulness and success of these meetings.

A special role in the scientific life of the institute was played by the Laboratory of Computational Mathematics headed by Shnol'. This laboratory had a very broad scope of research topics: from mathematical studies on stability theory, bifurcations of dynamical systems, and algebraic geometry to the development of compilers and the creation of bibliographical systems; from problems in the molecular dynamics of proteins and biological crystallography to the study of biochemical oscillations, wave propagation in active media, and papers on problems of blood coagulation. This was a sort of `incubator', from which independent laboratories and groups `gemmated' as they matured. A distinctive feature of Schnol's leadership was his deep understanding of the problems, combined with his complete trust in his young colleagues, his scientific freedom, and his support for initiative. He had the style of a truly strong leader: putting a lot of effort into administrative support of a project, while at the same time not interfering with its execution.

Several topics motivated by mathematical problems in the natural sciences (classical and quantum mechanics, astrophysics, biology) are traceable throughout the entire scientific career of Shnol'. These include the spectral theory of operators, the theory of stability and symmetry of differential equations, bifurcation theory, and extremal problems. Some of these topics are briefly discussed below. He ranked [5], [16], [24], [35], and [47] as being among his main mathematical papers.

While serving in the army and reading from Methods of mathematical physics by Courant and Hilbert at every opportunity, Shnol' became interested in the question of the relation between the mathematical and physical definitions of the spectrum of the Schrödinger operator. The answer came as the `Shnol' theorem': almost all points of the spectrum of the Schrödinger operator 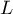$L$ (that is, almost all values 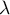$\lambda$ for which the operator 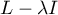$L-\lambda I$ does not have a continuous inverse) are eigenvalues, and the corresponding eigenfunctions grow at infinity no faster than a power function [4]. Gelfand said that this was the most important advance in the theory of Schrödinger operators after the celebrated 1910 paper of Hermann Weyl. The Shnol' theorem, which was repeatedly improved by the author himself [5], [6], gave impetus to many papers. It seems inconceivable that he could combine army service with first-class mathematical research!

For many years, Schnol's main scientific interests were connected with stability theory. His first paper on this topic was published in 1969, and the whole cycle of publications numbers about thirty, many of them written jointly with his student L. G. Khazin (see, for example, the monograph [30], or [35]). In analysing various critical cases, Shnol' discovered that the presence of a resonance can lead to the stabilization of an equilibrium that is unstable in the absence of a resonance. One of the central results of this cycle is a complete solution of the problem of stability of an equilibrium for degenerations up to codimension 3. Stability criteria for degenerations of codimensions 1 and 2 had been obtained by A. M. Lyapunov, G. V. Kamenkov, and others. For codimension 3 most of the criteria were obtained by Shnol' and Khazin. In particular, for one of the critical cases (two pairs of purely imaginary eigenvalues in a resonance 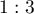${1:3}$) they proved [23] the non-existence of an algebraic stability criterion and thereby found the minimum codimension of a degeneration for which there can be algebraic insolubility of the stability problem discovered by V. I. Arnold in codimension greater than 100. It should be underscored that all degenerations were investigated by Shnol' together with neighbourhoods, and the sizes of `dangerous' and `safe' deviations from the equilibrium were estimated both in the phase space and in the space of parameters. This whole large cycle made up the contents of his D.Sc. dissertation ``Studies of stability of stationary motions'', defended in 1984.

Schnol's interest in classical mechanics problems was not confined to stability theory, he was also interested in questions about symmetries of dynamical systems in connection with Emmy Noether's celebrated theorem on first integrals. In particular, he studied (in the real-analytic situation) compact and semisimple Lie groups of symmetries of Hamiltonian systems with 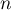$n$ degrees of freedom, and showed that the rank of such groups does not exceed 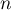$n$. As a consequence (by passing to the cotangent bundle) he showed that a semisimple real Lie group that acts on an 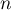$n$-dimensional manifold real-analytically (and effectively) has rank at most 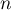$n$ (see [16]). (Another, more direct proof was given by Yu. G. Zarkhin later, in 1991.)

In the 1980s Shnol' studied the problem of synchronization of biochemical oscillators [31] in conjunction with co-workers in Sel'kov's laboratory in the Pushchino Institute of Biological Physics of the Russian Academy of Sciences. These investigations led to his interest in the question of bifurcations of auto-oscillations (limit cycles) in systems with symmetry. Together with his student E. V. Nikolaev, he considered in [44] the general problem of bifurcations of limit cycles in typical one-parameter families of systems having an arbitrary discrete symmetry group. Limit cycles in such systems were classified in accordance with how the natural continuous group of shifts along a periodic orbit interacts with a discrete symmetry group of the system, and a complete description of one-parameter bifurcations was also given for two classes out of three. In [45] equilibria were studied for equations that have a certain symmetry group, and the full bifurcation pictures were described for several of the simplest bifurcations. In particular, the possibility of the birth of a three-dimensional sphere from an equilibrium was shown.

A far-reaching generalization of Lyapunov's theorem on stability in the first approximation was obtained in the joint paper [48] with L. B. Ryashko. Instead of an equilibrium, they considered there a compact invariant manifold, and instead of the first approximation they considered the linearization of the `transversal component' of the differential equation. This is symbolic: Schnol's last mathematical paper completed the development of a certain branch of stability theory. Later on, Ryashko generalized the stability criterion obtained to stochastic differential equations.

In parallel with pure mathematics, Shnol' studied applied problems his whole life. In the 1960s he actively collaborated with the group of physicists headed by Zel'dovich at the Institute of Applied Mathematics. The research areas of this group touched upon very diverse problems: from the modelling of processes giving rise to explosions of supernova stars, to the most important problems in cosmology. These contacts continued over one and a half decades and were very fruitful. The first paper by Shnol' in the `astrophysical' cycle was devoted to a mathematical analysis of the problem of stability of a gaseous ball in its own gravitational field [12]. A similar problem, that of the gravitational stability of a dust cloud, was considered in a paper which he wrote with Khazin [11]. His next paper [21] was written with two astrophysicists (G. S. Bisnovatyi-Kogan and S. I. Blinnikov); there they considered the problem of stability of a star that is in one of unusual states near a phase transition, for example, in the pre-supernova state. Shnol's `signature' is distinctive in the rigorous mathematical statement of the problem and similarly rigorous conclusions. Shnol's results continue to be used by astrophysicists in the analysis of the physical state of stars that are in one or another critical state.

Another example of Shnol's fruitful collaboration with physicists is related to his investigation, together with V. D. Lakhno and A. N. Korshunova, of the critical states of an electron in a molecular cluster under the action of a strong magnetic field [46]. The model is described by a one-dimensional non-linear Schrödinger equation. They found the minimal size of a cluster for which there exists a localized solution. It was shown that as the radius of the cluster increases, it is possible that there co-exist two, three, or more solutions corresponding to localized states of the electron with different energies.

Shnol' had a lot of collaboration with people in the Institute of Chemical Physics of the Russian Academy of Sciences. The problem of propagation of cold flame was solved with his active participation [22]. We note that finding the speed of a laminar flame had long been a classical problem in mathematical physics, and it can be reduced to finding a trajectory connecting two singular points in phase space. In the case of one differential equation, the problem was solved by A. N. Kolmogorov, Zel'dovich, and others. For systems of equations this is a complicated computational problem which requires studying singularities and bifurcation points.

In the spring of 1966, in a seminar devoted to mathematical questions in the natural sciences at the Institute of Applied Mathematics, Shnol' expressed the following opinion: ``The theories of fluids are imperfect and do not always agree with each other. But couldn't we `look' at the structure of a fluid by calculating the interaction and motion of its molecules using a computer?'' This was the start of one of the first USSR projects on computer modelling of molecular dynamics, in which Shnol' took part together with A. G. Grivtsov and N. K. Balabanov. The first results were reflected in a series of preprints of the Institute of Applied Mathematics under the general title ``Numerical experiments on modelling the motion of molecules'' (see [15]). Nowadays, molecular dynamics is one of the main tools in molecular studies. We should note that the ideas and methods developed back then retain their significance to the present time. Shnol's best-known paper in this project is [20], in which the authors studied the motion of a free polymer chain and discovered an unexpected effect of increased mobility of end atoms (`hot ends effect').

In the 1980s Shnol' was engaged in a study of non-linear waves in active media (autowaves) by Pushchino biophysicist colleagues in Krinskii's laboratory. Computer calculations made it possible to find unexpected new diffraction properties of plane waves, for example, passing of every second autowave through a hole [33]. The paper [32] was devoted to studying vortices — solutions whose wave front rotates in a spiral (`spiral waves'). The behaviour of two interacting vortices was studied, and it was shown that, depending on the parameters of the model and the directions of rotation, vortices can be either moving along a common axis of symmetry, or rotating in a complicated manner about a common centre of symmetry.

Shnol's unique ability to see and understand a problem equally clearly in the language of the natural sciences and in the language of mathematics was decisive for further advances in this direction. For instance, he conjectured that in the theory of spiral waves one must use a classical principle: the equations of interaction of a particle with a field and the equations of evolution of the field itself must be derivable from one and the same fundamental equation. His students I. V. Biktasheva and V. N. Biktashev established an asymptotic theory of evolution of spiral waves as localized `particles' which predicts quantitatively the velocity of the drift of the spiral waves along with a number of new phenomena, for example, the orbits of precession about local inhomogeneities.⁵ An understanding of the evolution of vortices in simplified models helps one to interpret the results of numerical experiments in realistic models of cardiac arrhythmias and fibrillation.

Shnol's later papers written in collaboration with F. I. Ataullakhanov's team in the Hematology Research Centre of the Russian Academy of Medical Sciences were connected with the study of autowaves in the process of motion and coagulation of blood. The mathematical model of the `reaction-diffusion-convection' process included tens of equations, but in final form it was reduced to three non-linear partial differential equations. In this model the convection (blood flow) gave rise to paradoxical effects. For example, in a stationary medium an excitation wave decays, but in a non-uniformly moving medium an excitation wave propagates without damping. Another example: a wave propagates to a certain distance, and then transforms into a stationary structure. The study of the dependence of the behaviour pattern of this model on the parameters revealed a most complicated picture of bifurcations of space-time regimes [49], [51]. In the words of Ataullakhanov, ``We learned from Shnol' how to investigate the dynamics and bifurcations in complicated systems, and he learned from us, pedantically and in detail, about the biology and physics of coagulation. This was very unusual and beneficial.'' These studies gave birth to a new method of diagnostics and a device for finding disruptions of blood coagulation. And only very few people know how great was the contribution to these applied results by the brilliant mathematician Èmmanuil Shnol'.

The development of this direction of research led to the creation of a new detailed model of blood flow in a vessel that takes into account the presence of erythrocytes and thrombocytes in the blood composition, their size, shape, and other characteristics which can be measured experimentally. Shnol' actively participated in the project, going deeply into biological details, and he formulated questions for modelling and discussed methods for numerical analysis. The model made it possible to quantitatively explain the mechanism of localization of thrombocytes on the periphery of a vessel as a consequence of the presence of erythrocytes in the blood [56], and also the mechanism of adhesion of thrombocytes to the vascular wall and to a growing thrombocytary thrombus.⁶ The subsequent paper [57] describes the growth of a thrombus in a vessel and the dynamics of the blood flowing around the thrombus. As a result of these studies, it became possible to understand how nature solves the problem of localization of a thrombus in space, and to explain the mechanism of aggregation of thrombocytes in a blood flow.

Other joint papers⁷ of Shnol' and Ataullakhanov's team [50] were connected with the study of depolymerization of biological microtubules — protein intercellular structures which play an important role in the life and division of cells. These papers studied a model of the dynamics of polymerization (assembly) and depolymerization (disassembly) at different ends of a microtubule. It was predicted theoretically that in the process of depolymerization a microtubule can exert considerable forces and thus is an absolutely unique and new biological `motor'.

In a series of papers written jointly with A. S. Kondrashov, Shnol' proved three theorems in the theory of natural selection [37], [38], [55]. These results, known as `theorems of uncle Shnol' ' (Kondrashov is a nephew of È. È. Shnol'), are included as fundamental facts in lecture courses on evolutionary biology. In the 1970s Shnol' became the head of one of the first projects in the world on development of numerical methods, algorithms, and software programs for the investigation of bifurcations of dynamical systems [28].⁸ The need for such programs, aimed at general users, was dictated by the needs of mathematical modelling, in particular, in the early stages of the studies of oscillatory and chaotic regimes in biology. New theoretical results were discussed with enthusiasm by young IMPB co-workers at the seminar supervised by Shnol', where bifurcation scenarios were selected that are typical for applied problems. For these scenarios, algorithms and programs were developed (bifurcations of stationary solutions, limit cycles, and so on), and detailed descriptions of them were given. These publications, which were carefully edited by Shnol', were marked by clarity of exposition, and they remain valuable up to the present time. The Pushchino algorithms and software have been used in many laboratories in this country and abroad. They have become useful tools for studying bifurcations in problems in the natural sciences as well as in purely mathematical investigations.

Shnol' generously followed the wonderful tradition of gifting ideas (a feature of the Moscow mathematical school), adding to this tradition another rare quality. This was his need and his ability to help gain understanding of a subject which was often distant from his own. This he saw as an important obligation, for which he did not spare effort and time, and which manifested itself especially during the years of his work in Pushchino, when the spectrum of his interactions had broadened considerably, encompassing diverse branches of the natural sciences. He was distinguished by his desire and ability to understand papers by his colleagues, and in fact he often found connections that had not been noticed by the author. The seminars that he led worked in the same style, as did the annual scientific conferences of the RCC. A chat with Schnol' or a talk at a seminar with his participation could give a powerful impetus to the development of the work discussed.

Shnol' had an organic need to share knowledge — with colleagues of the most diverse specialities, with beginning researchers, with young people, and with schoolchildren. Pedagogy was his calling, along with mathematics. He taught his many students to understand `more the spirit than the letter' of the material that he presented, while remaining rigorous and accurate in every assertion. He also demanded the same attitude to teaching from his subordinates.

In co-authorship with Gelfand and E. G. Glagoleva, Shnol' wrote the pamphlet ``Functions and graphs'' [17], which was translated into five languages (including German, English, and Japanese). This has been a brilliant schoolbook for many generations of schoolchildren.⁹

Shnol's contacts with students were not confined to teaching mathematics but were a really multifaceted educational activity. Moreover, this was teaching a work style, being organized, interrelations with colleagues, scientific honesty, accuracy, and decency (``I can forget anything at all, except a promise''). It was impossible to be insincere with him. He was extremely scrupulous in questions of his authorship — the list of research papers with him as co-author should have been substantially longer.

Shnol' was an excellent teacher. Over his lifetime he gave many lectures for audiences of quite diverse ages: for schoolchildren in the framework of the Pushchino Lectorium (1982), for students during his work at the Moscow Institute of Physics and Technology (MIPT; 1966–1971), for young mathematician colleagues, and for quite mature colleagues, biologists, and physicists who needed a deeper understanding of mathematics for a more adequate description of the processes they were studying. The small book [36] was written on the basis of lectures he gave at the MIPT and in Pushchino on computational mathematics. However, by his own admission, he regarded seminars to be the most effective form of work: ``I am not good at lecturing, which is extremely difficult for me, but my thing is seminars. Seminars, or lessons at school, when there is feedback, when there is interaction with the audience''. A seminar in which Shnol' took part would usually end with him coming up to the blackboard, where over several minutes he would state, very concisely and clearly, both the problem and the results obtained (which the speaker himself did not always clearly articulate, especially a speaker from outside). Furthermore, he considered it to be a perfectly natural need to share his vast pedagogical experience. He would spend a long time working with people who had to talk before an audience, be it a defence of a dissertation, a talk at a conference, or a lecture for schoolchildren. One example of the wide range of his teaching activity was his seminar with the title ``Arnold's 100 Problems'', where problems presented in Arnold's note ``Mathematical Trivium'' in the course of a year were discussed.

Respect for the past, for memory, was another outstanding feature of Shnol'. For example, he gathered and, with his characteristic thoroughness, put in proper order audio, photo, and film materials that captured various events and celebrations. Now, many decades later, these documentations of the past are priceless. Thanks to him, the photographs and films collected, as well as various audio recordings, are now available for all those interested. In particular, the archive of the Shnol' family keeps photographs devoted to the closing ceremony of the Moscow Mathematical Olympiad of 1958, to the celebration of Gelfand's 60th birthday, and to many other events. He left numerous vivid and warm reminiscences both about internationally known people (Gelfand, Kronrod, Keldysh, Petrovskii, see [52]–[54]) and about his colleagues.

È. È. Shnol' passed away on 5 May 2014 in Pushchino. Those who were fortunate enough to be close to him in work or outside work will cherish memories of the joy of their relationship. As his school pupil Arnol'd Litvinov wrote: ``What he offered was open to everyone, everyone took what they could carry with them''.