Abstract
We study the time evolution of an incoherent mixture of quantum states and demonstrate, in very simple terms, a quantum mechanical equivalent of van Cittert–Zernike theorem, which can be easily explained to Quantum Physics students with a basic knowledge of the density matrix theory. Finally, we exemplify this result by applying it to the quantitative analysis of the coherence of a beam of particles in atomic collisions.
Export citation and abstract BibTeX RIS
1. Introduction
The Sun is a conspicuously incoherent source of light. However, when sunlight reaches the surface of the Earth after an 8 min journey, it exhibits spatial coherence over a length of tens of μm (Mashaal et al 2012). The explanation of this remarkable effect, where the light emitted from an incoherent source becomes approximately coherent at large distances, relies on a theorem (Born and Wolf 1999) demonstrated by van Cittert (1934) and, in a different context by Zernike (1938).
Based on a direct analogy between electromagnetic and de Broglie waves, this theorem from light optics is usually applied to the study of coherent properties of particle beams (Cronin et al 2009). This strategy of borrowing results from classical optics and applying them to the study of particle's coherence might be sound for qualitative analysis, but should be validated by a quantum mechanical approach for quantitative applications. For instance, an atom optics version of the van Cittert–Zernike theorem was proposed by Taylor et al (1994) in terms of a second-quantisation model. More recently, Impens and Guéry-Odelin (2010) employed a classical phase-space approach based on the truncated Wigner equation.
Anyway, the concept that a beam of particles can gain coherence with time is far from being easy to grasp. Here we present a very simple derivation of van Cittert–Zernike theorem for an incoherent mixture of quantum states. This demonstration aims to senior undergraduate students and relies on basic concepts of quantum mechanics, as the density matrix theory and the Born approximation in elastic collisions, as explained in standard textbooks (see, e.g. Schiff 1968, Landau and Lifshitz 1977, Galindo and Pascual 1990, Ballentine 2000, Bransden and Joachain 2000, Gasiorowicz 2003). We hope that this approach would provide Physics students with the understanding of a fascinating but rather counterintuitive concept.
In this article we study the time evolution of an incoherent mixture of an ensemble of particles of mass m, described by identical wave packets located at different positions upon a much larger region of dimension D. We evaluate the time evolution of the corresponding density operator ρ by solving the Liouville–von Neumann equation. Actually, we demonstrate that a coherence length ℓ can be defined, such that for distances shorter than ℓ the system behaves coherently (i.e. ρ can be approximated by the product of pure states). In particular, ℓ coincides with the coherence length of each individual wave packet for small times t, as expected; while for large values of t the standard expression  , of van Cittert–Zernike theorem is recovered. But first, let us review some basic concepts of the time evolution of an individual wave packet.
, of van Cittert–Zernike theorem is recovered. But first, let us review some basic concepts of the time evolution of an individual wave packet.
2. Free time evolution of a wave packet
Let us consider the time evolution of a normalised wave packet 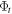 for a particle of mass m in the absence of a potential. For pedagogical reasons, let us assume that at time t = 0, the wave packet
for a particle of mass m in the absence of a potential. For pedagogical reasons, let us assume that at time t = 0, the wave packet 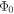 is separable in Cartesian coordinates, namely,
is separable in Cartesian coordinates, namely, 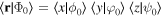 . Since this factorisation is preserved for all times, we will only study the evolution of
. Since this factorisation is preserved for all times, we will only study the evolution of  . However, it is important to point out that this assumption does not represent any loss of generality, since its removal is straightforward.
. However, it is important to point out that this assumption does not represent any loss of generality, since its removal is straightforward.
The calculation of the time evolution of 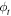 is trivial in momentum representation. It reads
is trivial in momentum representation. It reads

with 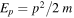 . The time evolution of the wave packet in coordinate space can be readily obtained,
. The time evolution of the wave packet in coordinate space can be readily obtained,

It is important to note that, since the momentum distribution does not depend on time, namely  , all the expectation values related to p are also time-independent,
, all the expectation values related to p are also time-independent,
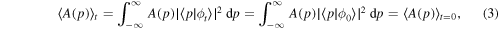
as expected for a free particle. In particular, so are 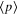 and
and 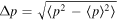 . On the contrary,
. On the contrary, 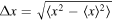 varies in time as (Robinett et al 2005)
varies in time as (Robinett et al 2005)
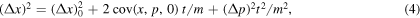
where we have defined the generalised covariance of two operators A and B as
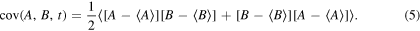
2.1. Gaussian wave packet
As a working example and for pedagogical reasons, from now on we will consider a Gaussian wave packet of initial full-width d (Kennard 1927, Darwin 1928, Lekner 2007, Cox and Lekner 2008), namely,

and

Replacing in equations (1) and (2), we obtain

and
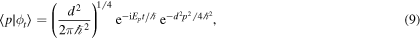
where we have defined

with 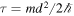 .
.
The expectation values of x and p are null, 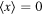 and
and  , and
, and 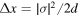 and
and 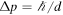 , which are in accordance with the general result, equation (4), i.e.
, which are in accordance with the general result, equation (4), i.e. 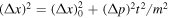 , for a null x–p covariance (Nicola 1972, Bradford 1976, Klein 1980). We see that the Gaussian wave function has its minimum value of
, for a null x–p covariance (Nicola 1972, Bradford 1976, Klein 1980). We see that the Gaussian wave function has its minimum value of 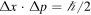 at t = 0, and then increases (for both positive and negative times) as
at t = 0, and then increases (for both positive and negative times) as

Let us point out that these latter results can be generalised to a wave packet of arbitrary form, whenever the characteristic time τ is redefined as  , as can be seen easily seen in equation (4).
, as can be seen easily seen in equation (4).
Finally, the Gaussian wave functions in space (8) and momentum (9) representations can be related by this simple equation, 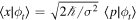 with
with 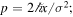 which, for
which, for 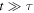 , reads
, reads
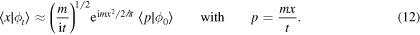
It can be easily shown, by means of a stationary phase approximation of (2), that this asymptotic limit is valid for any functional form of  (Dollard 1971), and not only for Gaussian wave functions. We will return to this general result in section 4.
(Dollard 1971), and not only for Gaussian wave functions. We will return to this general result in section 4.
2.2. Coherence length
When a compressed wave packet is colliding with a structured target, the result would strongly depend on the distance between the source of the projectiles and the target region. The reason is that if this distance is too short, then the wave packet might not illuminate the full target coherently, but only a portion of it. But as time goes by, the width of the wave packet will increase, until it reaches a critical distance, where all the target will be illuminated coherently.
To be more specific, let us consider that the wave interacts with two similar delta potentials separated by a given distance xo, namely 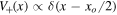 and
and 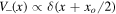 . In a first Born approximation (see, e.g. Schiff 1968, Landau and Lifshitz 1977, Galindo and Pascual 1990, Bransden and Joachain 2000, Gasiorowicz 2003), the cross section, proportional to the squared modulus of the transition matrix element
. In a first Born approximation (see, e.g. Schiff 1968, Landau and Lifshitz 1977, Galindo and Pascual 1990, Bransden and Joachain 2000, Gasiorowicz 2003), the cross section, proportional to the squared modulus of the transition matrix element  , would present an interference term given by
, would present an interference term given by
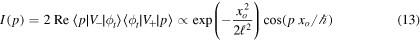
with

This term would be sizable for targets of the order of 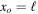 or smaller. Thus, we might define ℓ as the 'coherence' length of the wave function at a given time t. This definition, which relies on the conditions necessary for the appearance of an interference structure, is standard in optical studies (Svelto 2010), but still might differ from other diverse and even contradictory definitions. For instance, Cohen-Tannoudji and Guéry-Odelin (2011) define the coherence length as the width of the global spatial coherence,
or smaller. Thus, we might define ℓ as the 'coherence' length of the wave function at a given time t. This definition, which relies on the conditions necessary for the appearance of an interference structure, is standard in optical studies (Svelto 2010), but still might differ from other diverse and even contradictory definitions. For instance, Cohen-Tannoudji and Guéry-Odelin (2011) define the coherence length as the width of the global spatial coherence,

corresponding to the overlapping between two wave packets separated by a distance xo. For a Gaussian wave packet (equations (8) and (9)) we obtain, 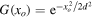 . Thus, in the approach by Cohen-Tannoudji and Guéry-Odelin (2011), the coherence length is time-independent and equal to d.
. Thus, in the approach by Cohen-Tannoudji and Guéry-Odelin (2011), the coherence length is time-independent and equal to d.
Here, on the contrary, we retain the definition (14). Note that the more sharply peaked the wave packet is at t = 0 (i.e. for smaller values of d), the faster its coherence length spreads (for  ) since
) since

As a side comment, let us point out that in optics this limit is named in honor of Joseph von Fraunhofer, although he was not actually involved in the development of the theory. Putting some numbers; let us consider an electron impulsively removed from the ground state of a hydrogen atom. For a corresponding initial width of d = 1 Å the time necessary to achieve condition (16) is in the range of tens of attoseconds (i.e. 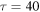 as), whereas the coherence length increases at a constant rate,
as), whereas the coherence length increases at a constant rate, 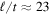 km s−1.
km s−1.
Finally, let us assume that the wave has a group velocity 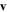 , such that it travels a distance
, such that it travels a distance 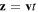 in a given time t. Even thought we are considering a one-dimensional problem, v might not be necessarily parallel to the direction
in a given time t. Even thought we are considering a one-dimensional problem, v might not be necessarily parallel to the direction  . We will come back to this point in the following section. Now, replacing
. We will come back to this point in the following section. Now, replacing 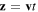 in the previous equation, we obtain,
in the previous equation, we obtain,

with 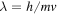 the particle's wavelength.
the particle's wavelength.
3. Time evolution of an incoherent mixture of wave packets
Let us now consider the free evolution of an incoherent mixture of an ensemble of particles described by wave packets 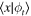 , as defined in (2), which are identical except for their initial positions b, which are distributed along the x axis according to a normalised distribution f(b). Initially (i.e. at t = 0), the corresponding density operator
, as defined in (2), which are identical except for their initial positions b, which are distributed along the x axis according to a normalised distribution f(b). Initially (i.e. at t = 0), the corresponding density operator 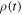 reads,
reads,
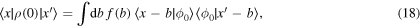
in space representation, and 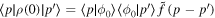 in momentum representation, with
in momentum representation, with 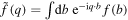 .
.
As in the previous sections, and for the sake of simplicity, we are considering a one-dimensional case. This does not mean any loss of generality, since the generalisation to the three dimensional case is straightforward. The density operator 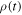 evolves in time according to the the Liouville–von Neumann equation with a free Hamiltonian Ho,
evolves in time according to the the Liouville–von Neumann equation with a free Hamiltonian Ho,

This equation is trivially solved in momentum representation, namely

with 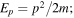 from which the time dependent expression for the space dependent matrix element can be easily obtained,
from which the time dependent expression for the space dependent matrix element can be easily obtained,

3.1. Gaussian wave packet and impact parameter distribution
In what follows, we will consider that both the wave packets ϕ and the distribution f(b) are of a Gaussian shape, namely,

and

Thus, in momentum representation,
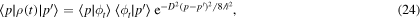
with 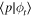 given by (9), namely,
given by (9), namely,
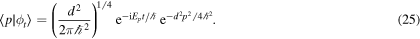
Similarly, in space representation,
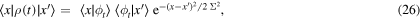
where

with 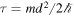 , and
, and

with

Let us note that in both space and momentum representations, the density matrix (26) is composed of a Gaussian pure state, incoherently modulated by a Gaussian distribution of standard deviation Σ. We will come back to this result in the following section. But first, let us notice that, as expected,
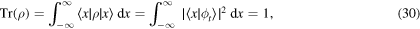
while

so that the total coherence of the beam remains constant in time. Let us point out that a simple calculation in momentum space can show that 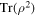 is independent of time, independently of the functional forms employed for
is independent of time, independently of the functional forms employed for 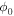 and f(b).
and f(b).
3.2. Emerging coherence from an incoherent mixture of wave packets
It is clear that for 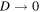 , the width Σ of the modulating Gaussian reaches infinity, and the system becomes completely coherent, consisting of a single Gaussian wave centred at x = 0. The corresponding density matrix element reads
, the width Σ of the modulating Gaussian reaches infinity, and the system becomes completely coherent, consisting of a single Gaussian wave centred at x = 0. The corresponding density matrix element reads

with a wave function given by (8), i.e.

where

Without going all the way to this purely coherent case, we see that for any finite value of Σ it would be possible to define a characteristic distance for which, if  is smaller than it, the modulating Gaussian would be approximately constant and the system would mimic a completely coherent state. The emergence of this spatial coherence out of an incoherent system is the essence of the van Cittert–Zernike theorem.
is smaller than it, the modulating Gaussian would be approximately constant and the system would mimic a completely coherent state. The emergence of this spatial coherence out of an incoherent system is the essence of the van Cittert–Zernike theorem.
Now, we find the same dependence on xo for the interference term (13) than the one obtained in the previous section, i.e.
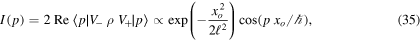
but with a different coherence length,

Note that for D = 0, we recover the same result obtained in the previous section for a purely coherent system.
As a marginal note, let us point out that, when dealing with the concept of spatial coherence, the corresponding coherence length ℓ might be defined as the distance between two points in space for which the right term in (35) is a given fraction ξ of its maximum value. Thus, in general, we might define

A standard definition is that of the full-width at half-maximum, for which 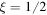 . In our case, we have arbitrarily chosen
. In our case, we have arbitrarily chosen 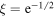 , so that (36) is obtained.
, so that (36) is obtained.
3.3. Small and large t limits
For very small values of t (a limit that in optics is usually named after Augustin-Jean Fresnel), we obtain  . This means that the coherence length is limited to that of an individual wave packet. On the contrary, for
. This means that the coherence length is limited to that of an individual wave packet. On the contrary, for 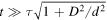 , it grows linearly with time as
, it grows linearly with time as

Let us also point out that in general situations, 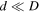 . This is the case, for instance, in particle accelerators, where the projectile's wave packets are much smaller than the macroscopic size of the collimators. In these cases, for
. This is the case, for instance, in particle accelerators, where the projectile's wave packets are much smaller than the macroscopic size of the collimators. In these cases, for 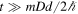 , we can approximate (36) by
, we can approximate (36) by

Finally, replacing 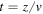 , we write equations (36) and (39) as
, we write equations (36) and (39) as

and

respectively, with 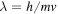 the particle's wavelength. As we already mentioned in a previous section, the velocity
the particle's wavelength. As we already mentioned in a previous section, the velocity 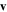 is not necessarily parallel to x. For instance, in the standard geometry of the collision experiments, the beam of particles is moving in a direction perpendicular to that of the impact parameter
is not necessarily parallel to x. For instance, in the standard geometry of the collision experiments, the beam of particles is moving in a direction perpendicular to that of the impact parameter 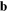 , a situation that is usually referred to as of 'transversal' coherence.
, a situation that is usually referred to as of 'transversal' coherence.
Finally, let us point out that by comparing equations (14) and (36), we see that the coherence length grows at a much faster rate for a coherent state than in an incoherent superposition. In particular, for large values of t, the corresponding ratio becomes proportional to 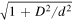 . This characteristic of the coherence length evolution is already evident when comparing the generalised widths σ in equations (8) and (26).
. This characteristic of the coherence length evolution is already evident when comparing the generalised widths σ in equations (8) and (26).
4. Non-Gaussian wave functions and position distribution
In the previous sections, we have assumed Gaussian shapes for the initial position distribution f(b) and the wave packets ϕ. The reason for this choice was purely pedagogical, since all the calculations can be performed analytically. In this respect let us point out that this analysis in terms of Gaussian functions is simple enough as to be included in a problem to be solved by the student. However, it is important to point out that most of the results obtained with Gaussian functions are also valid for general non-Gaussian f(b) and ϕ functions. Take equation (39), for instance; one of the main results associated to the van Cittert–Zernike theorem. By replacing the general asymptotic form (12) of the wave function in the interference term (13), a simple demonstration leads to 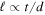 for pure states. Similarly, replacing (12) in (35), and performing a straightforward change of the integration variable, it can be shown that for an incoherent mixture of wave functions,
for pure states. Similarly, replacing (12) in (35), and performing a straightforward change of the integration variable, it can be shown that for an incoherent mixture of wave functions,

for large values of t. Perhaps, this latter demonstration is too cumbersome to be of any pedagogical value. However, it can be numerically tested for different functional forms of f(b) and ϕ, providing a complementary avenue for exploration and/or exercises.
5. Conclusions
We have shown in section 3 that it is possible to develop a generalisation of van Cittert–Zernike theorem for massive particles, as a direct application of the density matrix concept. In particular, we see that this analysis does not imply any difficulty greater than those encountered in the study of the coherence length of a pure state, as shown in section 2. Furthermore, similar results are obtained in both cases, but with the difference that for large values of t the characteristic distance for the incoherent mixture is the size D of the source, instead of the initial width d of each of its individual waves. The reason for this result is that coherence emerges as result of the superposition of each of the individual components of the mixture. In spite of its simplicity, this difference is transcendental, and goes to the very heart of the van Cittert–Zernike theorem. It makes the coherence length of the sunlight to be of the order of tens of μm, instead of larger than the Earth itself, as it would be for each of its individual photons. The same occurs in a particle accelerator, where the coherence length at the target region is of atomic dimensions and can be varied by changing its relative position along the beam's line. Recently, this peculiarity of the van Cittert–Zernike theorem has made it possible to develop a new set of atomic and molecular collision experiments where the cross sections are shown to depend on the degree of coherence of the projectiles beam. The coherence properties of particle beams have been extensively studied for decades, most notably in connection with neutrino interference and oscillations (Nussinov 1976, Kayser 1981), but represents a rather new issue in the area of atomic collisions (Egodapitiya et al 2011). It has been usually assumed that under very general and common conditions, the outcome of a scattering experiment does not depend on the properties of the projectiles beam (Taylor 1972). However, recent evidence in ionisation (Egodapitiya et al 2011) and electron capture (Sharma et al 2012) experiments points to a breakdown of these conditions and a dependence of the collision outcome on the incident beams coherence properties. Finally let us point out that in the present article we have focussed our attention on the dependence of the spatial degree of coherence with the distance to the source, but not on its intensity distribution. This element of van Cittert–Zernike theorem is relevant in optics, but not in its application to atomic collision experiments, where the projectile's beam is assumed to be homogeneously distributed over the transversal plane.
Acknowledgments
This work was supported by Universidad Nacional de Cuyo (Grant 06/C480) and by the National Scientific Research Foundation (OTKA, Grant No. K109440).


