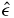Abstract
The loudest event statistic, a method by which the rate at which events occur can be deduced from the significance of the most significant event (or loudest event), has been employed in several papers describing the search for gravitational waves produced by coalescing compact binaries in data from the LIGO and Virgo observatories. The paper 'The loudest event statistic: general formulation, properties and applications' (Biswas et al 2009 Class. Quantum Grav. 26 175009) presents a general formulation of the loudest event statistic and addresses topics on the estimation of rate intervals, on combining multiple experiments, and on marginalizing over uncertainties in parameters. A conceptual error in section 5 of Biswas et al (2009) led to invalid results regarding the marginalization over uncertainties in the averaged detection efficiency; specifically its equations (23) and (24) are incorrect, as are its equations (25) and (27). This corrigendum presents a correct treatment of the marginalization of uncertainties in the estimated detection efficiency.
Export citation and abstract BibTeX RIS
During the internal collaboration review of the search for gravitational waves from low mass compact binary coalescence in LIGO's sixth science run and Virgo's science runs 2 and 3 [2], an inconsistency in results obtained from two different methods of marginalization over uncertainties in the measured value of the search's detection efficiency revealed there was an error in section 5.1, equations (23) and (24), of [1]. Here we provide a correct version of section 5.1 of [1]. At the end we give the trivial correction to section 5.2.
Our discussion begins with equation (11) of [1], which expresses the posterior distribution for the mean number of true (astrophysical) events μ with a ranking statistic above some largest observed loudness parameter  (the 'loudest event') as
(the 'loudest event') as
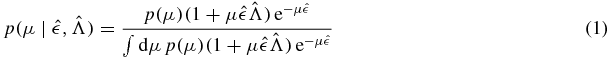
where  is the average detection efficiency function evaluated at the ranking statistic value of the loudest event observed, and
is the average detection efficiency function evaluated at the ranking statistic value of the loudest event observed, and  is a measure of the relative probability of the loudest event arising from a foreground signal versus such an event occurring due to the experimental background; a value
is a measure of the relative probability of the loudest event arising from a foreground signal versus such an event occurring due to the experimental background; a value  results if the loudest event is definitely from the background, and
results if the loudest event is definitely from the background, and  in the limit that the loudest event is definitely from the foreground. The function Λ(x) is defined by equation (12) of [1]. A Poisson-distributed foreground rate with mean number of events μ is assumed, while p(μ) is the prior unconditional probability distribution for this quantity. The detection efficiency
in the limit that the loudest event is definitely from the foreground. The function Λ(x) is defined by equation (12) of [1]. A Poisson-distributed foreground rate with mean number of events μ is assumed, while p(μ) is the prior unconditional probability distribution for this quantity. The detection efficiency  (x) is a monotonic function of the ranking statistic x that describes the probability that a single foreground event provided by nature will have a ranking statistic at least as significant as the value x; therefore, it is equivalent to describe events in terms of the detection efficiency variable
(x) is a monotonic function of the ranking statistic x that describes the probability that a single foreground event provided by nature will have a ranking statistic at least as significant as the value x; therefore, it is equivalent to describe events in terms of the detection efficiency variable  , and, in particular, the loudest event will have the value
, and, in particular, the loudest event will have the value  , which is the smallest value of
, which is the smallest value of  that occurs during the experiment.
that occurs during the experiment.
Equation (1) is obtained from the likelihood function,

via the application of Bayes's theorem,
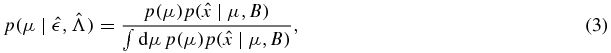
where B indicates dependence of the probability distribution on the background. The function p0(x) is the unconditional probability distribution of the experimental background producing an event having a loudest event x, while the function p(x∣μ, B) is the probability distribution for x in an experiment having both a background and a foreground as described above. All dependence of the posterior distribution on the background is contained in the value  .
.
Section 5.1 of [1] was concerned with the situation in which the value of  is not known exactly6. Suppose that the true value of efficiency is related to the measured value via a factor α so that
is not known exactly6. Suppose that the true value of efficiency is related to the measured value via a factor α so that

Given an observed loudest event, and consequently a value of  , we wish to infer the value of the efficiency and also the posterior distribution for μ. We suppose that, for a given
, we wish to infer the value of the efficiency and also the posterior distribution for μ. We suppose that, for a given  , the probability distribution for the true (but unknown) efficiency
, the probability distribution for the true (but unknown) efficiency  is
is  . For simplicity, and in keeping with [1], we choose the gamma-distribution,
. For simplicity, and in keeping with [1], we choose the gamma-distribution,

where the two parameters θ and k determine the mean, kθ, and the variance, kθ2 (cf equation (22) of [1]). If we assume that the mean of this distribution is equal to the measured value of the efficiency  , then we fix the scale parameter to be
, then we fix the scale parameter to be  to obtain
to obtain  ; the shape parameter k then specifies the width of the distribution. When k is large, the gamma-distribution will be sharply-peaked about its mean value. Equation (5) can be re-expressed as a probability distribution for the scale factor α in equation (4) as
; the shape parameter k then specifies the width of the distribution. When k is large, the gamma-distribution will be sharply-peaked about its mean value. Equation (5) can be re-expressed as a probability distribution for the scale factor α in equation (4) as

The scale factor α is a random variable describing the uncertainty in the measurement of the efficiency. We must now derive a modified version of equation (1) that accounts for this additional random variable. We may either (i) construct a marginal likelihood by marginalizing over this uncertainty in the likelihood function and then proceed to use Bayes's theorem to obtain a posterior distribution for μ, or (ii) treat α as a nuisance parameter in the posterior distribution (see, e.g., section 36.1.4.2 of [3]). These should yield the same result, but it is instructive to derive the result using both methods.
We employ method (i) first. We use equations (2) and (4) to write the likelihood function
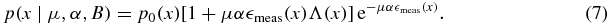
We now construct a marginal likelihood, p(x∣μ, k, B), by marginalizing over α,
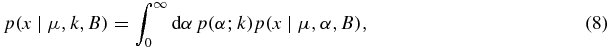
and using our gamma-distribution for α we find
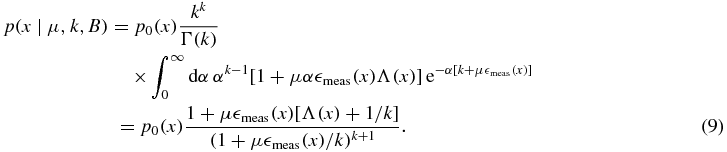
Note that in the limit k → ∞ we recover equation (2) with  (x) replaced with
(x) replaced with  meas(x). We now obtain a posterior distribution for μ from Bayes's theorem,
meas(x). We now obtain a posterior distribution for μ from Bayes's theorem,
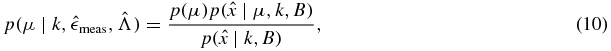
where the marginal probability for x is
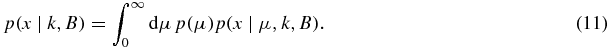
For illustration we take a uniform prior, p(μ) = const, cf equation (13) of [1]. We have
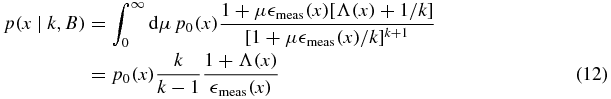
and therefore the posterior distribution is
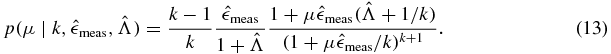
Equation (13) is the correct version of equation (24) of [1].
An alternative, but equivalent, method of handling the parameter α is to use method (ii) above, and treat it as a nuisance parameter in a posterior distribution  and to integrate it out:
and to integrate it out:
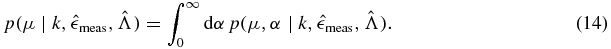
From Bayes's theorem, we see that the posterior with the nuisance parameter is given by
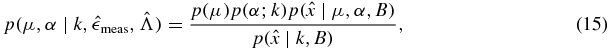
where
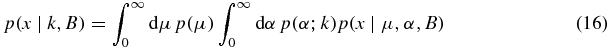
is exactly the marginal probability for x given earlier, as can be seen by substituting equation (8) into equation (11). Finally, inserting equation (15) into equation (14) gives us
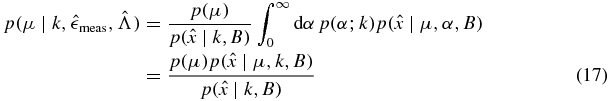
which is the same as equation (10). As expected we obtain the same final result for the posterior distribution if we consider α to be a nuisance parameter that we integrate out or if we marginalize the likelihood over the parameter α.
We can now explain the mistake in [1]. Note that we had to modify equation (1) to account for the addition of the random variable α, while [1] used its equation (11) without modification. Thus the substitution of equation (11) into equation (23) in [1] is not equivalent to the fundamental definition of the marginalized posterior, given by equation (10) or (14) here.
The same mistake was made in section 5.2 of [1]. Its equation (25) is the incorrect starting point. Instead, if we suppose Λ(x) = βΛmeas(x) where β is a random variable with expectation value of unity, then it is straightforward to get the correct result following the methods explained here. The easiest approach is to first compute the marginal likelihood, which in this case is obtained by substituting Λ(x) = βΛmeas(x) in equation (2), multiplying by p(β), and integrating over β. The result has the exact same form with Λ(x) → Λmeas(x). It then follows that the correct version of equation (27) in [1] is its equation (14) with this same substitution. Thus, the posterior marginalized over uncertainties in  does not depend on the variance of this uncertainty at all (provided that the expectation value of β is unity), and equations (26) and (28) in [1] are superfluous. This also means marginalizing over uncertainties in
does not depend on the variance of this uncertainty at all (provided that the expectation value of β is unity), and equations (26) and (28) in [1] are superfluous. This also means marginalizing over uncertainties in  will not change upper limits on the rate at all. The conclusion of section 5.2 of [1] is still correct: marginalization over uncertainties in
will not change upper limits on the rate at all. The conclusion of section 5.2 of [1] is still correct: marginalization over uncertainties in  can be neglected.
can be neglected.
Acknowledgments
We would like to acknowledge many useful discussions with members of the LIGO Scientific Collaboration that took place during the internal collaboration review of [2] which led to the discovery of the error in [1]. This work has been supported in part by NSF grant PHY-0970074. SF would like to thank the Royal Society for support.
Footnotes
- 6
In the context of gravitational wave searches, such as the one described in [2], the search efficiency is estimated using Monte Carlo methods in which simulated signals from a hypothetical distribution are added to the detector noise, and the fraction of such signals with ranking statistics greater than the loudest event's is the measured value of
 ; this value has a measurement uncertainty due to the finite number of trials performed.
; this value has a measurement uncertainty due to the finite number of trials performed.