Table of contents

The Burgers equation with moving boundary is considered on the semiline . The initial/boundary value problem is solved in the case of the Neumann problem and with a flux-type boundary condition.

Given the Laplace transform F(s) of a function f(t), we develop a new algorithm to find an approximation to f(t) by the use of the classical Laguerre polynomials. The main contribution of our work is the development of a new and very effective method to evaluate the Laguerre coefficients with the use of the Riemann zeta function. Some examples are illustrated.

The problem of determining a simple boundary from given Cauchy data is studied. This problem may be relevant in two-dimensional electrical impedance tomography where reconstructions of both the conductivity and the boundary are sought. It is found that under certain restrictions on the data, a one-parameter set of boundaries can be obtained in closed form. An immediate consequence of this result is that this problem does not have a unique solution. We make some comments on how to solve the problem with more generalized Cauchy data that do not necessarily obey the restrictions given.

This paper addresses the problem of image reconstruction from limited Fourier data. An improved parameter estimation algorithm is proposed for use with a polynomial model-based image reconstruction method. Results from magnetic resonance imaging data are shown to demonstrate the performance of the proposed algorithm.

Propagation of a transversely polarized time-harmonic electromagnetic plane wave in a stratified nonreciprocal chiral (bi-isotropic) slab under oblique incidence is considered. The inverse problem of reconstruction of material characteristics of a medium is studied. A reconstruction procedure is given and a uniqueness theorem is proven.

Taking the parameter b to vary along a monoparametric family of planar curves, given in the form , ( being the parameter along each specific curve of the family), we derive two equations to formulate the inverse problem of dynamics and find all potentials creating, for adequate initial conditions, the given family. One of these equations offers the total energy on each specific orbit traced under a known potential, the other equation relates merely potentials and orbital data. This later equation lends itself to series expansion solutions for small values of the parameter b.

Two applications to isotach and geometrically similar orbits are discussed as special cases and two examples are given to demonstrate the efficiency and the indispensability of the new equations.

In this paper we are concerned with a quasilinear parabolic equation with nonhomogenous Cauchy and Neumann conditions arising in combustion theory: by the Schauder fixed-point theorem we give a local existence result for the solution to an inverse problem on a semi-infinite strand.

We consider the determination of the interior domain where D is characterized by a different conductivity from the surrounding medium. This amounts to solving the inverse problem of recovering the piecewise constant conductivity in from boundary data consisting of Cauchy data on the boundary of the exterior domain . We will compute the derivative of the map from the domain D to this data and use this to obtain both qualitative and quantitative measures of the solution of the inverse problem.

In this paper, we investigate the numerical identifications of physical parameters in parabolic initial-boundary value problems. The identifying problem is first formulated as a constrained minimization one using the output least squares approach with the -regularization or BV-regularization. Then a simple finite element method is used to approximate the constrained minimization problem and the convergence of the approximation is shown for both regularizations. The discrete constrained problem can be reduced to a sequence of unconstrained minimization problems. Numerical experiments are presented to show the efficiency of the proposed method, even for identifying highly discontinuous and oscillating parameters.

Functions with (linear) phase depend on (linear) combinations of the independent variables. For example plane waves are functions of a single linear combination of the variables. Detection of phase is an important problem in seismic velocity analysis and ocean acoustic signal processing, amongst other applications. Robust estimation of phase by local optimization requires the construction of smooth objective functionals. For this purpose it is useful to characterize those quadratic functionals of functions with linear phase which are smooth in the phase: all such smooth phase detectors are pseudodifferential. Some of these pseudodifferential quadratic forms are globally convex in the phase, hence permit phase estimation using local smooth optimization methods.

Nonlinear propagation of electromagnetic waves is an important problem in optics. Often the properties of the nonlinear media are not fully understood. The solution of an inverse problem can provide an aid to that understanding.

An inverse transmission problem is posed; it is one of reconstructing the medium parameters, by measurement of a wave that has been propagated through the nonlinear medium. The nonlinear medium is assumed to be homogeneous and isotropic. The methods have application to nonlinear optics, and the numerical results for both the direct and inverse problems presented are based on the nonlinear Kerr effect, which is observed in the optical wavelength band. However, the mathematical techniques that are developed are applicable to any set of nonlinear first-order equations. The method is therefore model independent.

In electrical impedance tomography the boundary shape is often inaccurately known. If the boundary shape is wrong (in a three-dimensional problem) there will not generally be an isotropic conductivity which fits the current and voltage data. Both the conductivity and boundary shape can be determined by electrical data together with three spatial measurements. In two dimensions errors in boundary shape could be accounted for by a change in conductivity, but not if the length scale on the boundary is also known.

We consider a parameter choice method (called the minimum bound method) for regularization of linear ill-posed problems that was developed by Raus and Gfrerer for the case with continuous, deterministic data. The method is adapted and analysed in a discrete, stochastic framework. It is shown that asymptotically, as the number of data points approaches infinity, the method (with a constant set to 2) behaves like an unbiased error method, which selects the parameter by minimizing a certain unbiased estimate of the expected squared error in the regularized solution. The method is also shown to be weakly asymptotically optimal, in that the `expected' estimate achieves the optimal rate of convergence with repect to the expected squared error criterion and it has the optimal rate of decay.

Several prominent methods have been developed for the crucial selection of the parameter in regularization of linear ill-posed problems with discrete, noisy data. The discrepancy principle (DP), minimum bound (MB) method and generalized cross-validation (GCV) are known to be at least weakly asymptotically optimal with respect to appropriate loss functions as the number n of data points approaches infinity. We compare these methods in three other ways. First, n is taken to be fixed and, using a discrete Picard condition, upper and lower bounds on the `expected' DP and MB estimates are derived in terms of the optimal parameters with respect to the risk and expected error. Next, we define a simple measure of the variability of a practical estimate and, for each of the five methods, determine its asymptotic behaviour. The results are that the asymptotic stability of GCV is the same as for the unbiased risk method and is superior to that of DP, which is better than for MB and an unbiased error method. Finally, the results of numerical simulations of the five methods demonstrate that the theoretical conclusions hold in practice.

This paper considers the problem of vector tomography on an arbitrary bounded domain in three dimensions. The probe transform of a vector field is the inner product of the Radon transform of a vector field with a unit vector, called the probe, which may be a function of the projection orientation. Previous work has given reconstruction formulae for arbitrary fields and for those known to be divergence-free or curl-free in the case that the field is zero on its boundary. This paper considers the possibility that the field may not be zero on its boundary and may, therefore, have a harmonic component, which is both divergence-free and curl-free. It is shown that the curl-free component can be reconstructed using only one probe measurement and the divergence-free component can be reconstructed using only two probe measurements. No boundary measurements are necessary.

We prove a stability estimate for an inverse acoustic backscattering problem. This inverse problem consists of the determination of the sound speed, which is in the principal part of the equation, by the backscattering data. Previously, the stability estimates for inverse problems dealing with the unknown coefficient in the principal part of the equation were of logarithmic or Hölder type. Here we are able to obtain a Lipschitz-type estimate for this inverse backscattering problem.

There is an error in theorem 2.1 of this paper, which shows a representation of the Fréchet derivative with respect to the boundary of the far field operator from scattering by obstacles with Robin boundary conditions. The boundary condition in equation (2.4) has to be replaced by

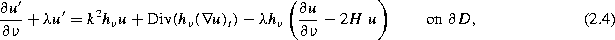
where H denotes the mean curvature of the boundary.

The error occurs in the derivation of equation (2.12). Therefore the proof of theorem 2.1 presented in this paper has to be modified on pages 376-7 along the following lines.

For the surface integral we obtain

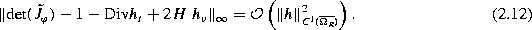
This can be seen by considering a fixed point 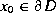and a local parametrization , of with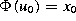

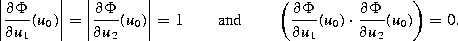
The perturbed boundary is then locally described by 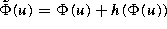. We compute at the point U₀

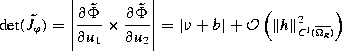
with

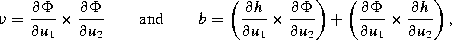
and the orthonormality of the tangential vectors leads to

We obtain

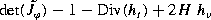
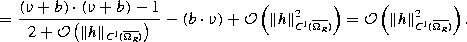
This holds independently of the parametrization and uniformly on .

With the estimates (2.10)-(2.12) we first see from (2.8) by a perturbation argument that tends to u in 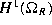. This is well known: the scattered field depends continuously on the boundary, or in our notation F_R is a continuous operator (cf Kress and Zinn (1992) for the Dirichlet problem). Therefore, with equation (2.8) the proof is completed by showing

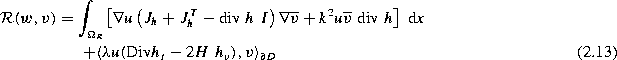
for all v.

Since u' is a radiating solution of (2.3)-(2.4) we obtain from the boundary condition

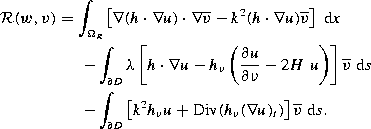
Now we proceed as in the paper with the only modification of adding the integral

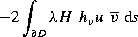
in any following computation of the sesquilinear form 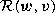. This rectifies the proof.

Reference

Kress R and Zinn A 1992 On the numerical solution of the three-dimensional inverse obstacle scattering problem J. Comput. Appl. Math.42 46-61