Table of contents

Inverse problems play a crucial role in geophysics because one of the main tasks in this field is to probe the Earth's interior both for economic reasons, such as oil prospecting, and for the pursuit of academic knowledge about our planet. A variety of different physical fields are used for this: elastic waves form the basis of seismic prospecting, electromagnetic or magnetic fields are used to make inferences about the electrical conductivity in the Earth and the magnetic properties of the core, the gravity field constrains the mass distribution within the Earth, and many other examples can be given where inverse problem theory is crucial for inferring the properties of the Earth from measurements at its surface. Examples of the theory and practice of geophysical inverse problems are given by Iyer and Hirahara (1993), Lines and Levin (1988) and Parker (1994).

This special section is aimed at presenting the inverse problems community with the theoretical barriers that geophysicists encounter, and providing some unorthodox examples of geophysical inverse problems. Every image obtained from an inverse problem with an incomplete data set gives an incomplete impression of the object under consideration. Trampert shows how limitations in global tomography influence the interpretation and implications of global maps of the seismic velocity in the Earth. In addition he shows how difficult it is to quantify the limitation of the images that are obtained. As shown by Snieder, nonlinearity aggravates this problem. He makes the point that currently there are no satisfactory theoretical tools for the error and resolution analysis of truly nonlinear inverse problems. Mosegaard attacks this problem, not by seeking a single solution to inverse problems, but by constructing many models and making inferences on the likelihood of these models using Bayesian statistics. That such an approach is needed for many practical problems is shown by Sambridge who shows that in practical problems the misfit function (or probability density function) can be extremely complex. In addition he develops tools to characterize this complexity. That inverse problem theory can be applied to problems other than making images of the Earth's interior is shown by Peltier, who makes inferences about the viscosity in the Earth from the measurement of sea-level variations, and by Gallagher, who reconstructs the thermal history of oil reservoirs from measurements at the surface. A major challenge in geophysics is to use different datasets to make inferences about the Earth's interior. Barghazi and Sansó present theoretical tools that can be used for the joint inversion of seismological and gravity data.

It will be clear from this special section that inverse problems is a rich and diverse field of research within geophysics. Despite the success of many of its applications (western industrial society would not exist without effective methods for seismic exploration), geophysicists run into theoretical barriers. Within the geophysics community, solutions are usually sought that rely heavily on numerical techniques. It could be that this is the wisest strategy. However, it is also likely that an increased interaction with theoreticians who are active in the field of inverse problems could be beneficial both for the geophysics community and for those active in inverse problem theory. The goal of this special section is to help to close the gap between theory and practice within the inverse problems community.

References

Iyer H M and Hirahara K (ed) 1993 Seismic Tomography; Theory and Practice (London: Chapman and Hall)

Lines L R and Levin F L (ed) 1988 Inversion of Geophysical Data SEG reprint series, 9

Parker R L 1994 Geophysical Inverse Theory (Princeton, NJ: Princeton University Press)

Global seismic tomography has produced a great amount of robust information concerning the three-dimensional extent of the Earth's internal structure. This has stimulated a multidisciplinary discussion aimed at understanding the mechanisms which govern the internal evolution of our planet. A brief overview of seismic tomography is presented. Since geodynamical understanding is the main purpose of seismic tomography, some suggestions are made on how to evolve from a predominantly qualitative to a more quantitative interpretation of its results. We argue that without a more systematic and realistic error and resolution analysis, interpretations might be misleading. Assuming a steady increase of data quality and coverage, the most challenging aspect of seismic tomography will be to take the nonlinearity of the problem fully into account. It is hoped that this contribution stimulates some discussion in that direction.

In many practical inverse problems, one aims to retrieve a model that has infinitely many degrees of freedom from a finite amount of data. It follows from a simple variable count that this cannot be done in a unique way. Therefore, inversion entails more than estimating a model: any inversion is not complete without a description of the class of models that is consistent with the data; this is called the appraisal problem. Nonlinearity makes the appraisal problem particularly difficult. The first reason for this is that nonlinear error propagation is a difficult problem. The second reason is that for some nonlinear problems the model parameters affect the way in which the model is being interrogated by the data. Two examples are given of this, and it is shown how the nonlinearity may make the problem more ill-posed. Finally, three attempts are shown to carry out the model appraisal for nonlinear inverse problems that are based on an analytical approach, a numerical approach and a common sense approach.

The general inverse problem is characterized by at least one of the following two complications: (1) data can only be computed from the model by means of a numerical algorithm, and (2) the a priori model constraints can only be expressed via numerical algorithms. For linear problems and the so-called `weakly nonlinear problems', which can be locally approximated by a linear problem, analytical methods can provide estimates of the best fitting model and measures of resolution (nonuniqueness and uncertainty of solutions). This is, however, not possible for general problems. The only way to proceed is to use sampling methods that collect information on the posterior probability density in the model space. One such method is the inverse Monte Carlo strategy for resolution analysis suggested by Mosegaard and Tarantola. This method allows sampling of the posterior probability density even in cases where prior information is only available as an algorithm that samples the prior probability density. Once a collection of models sampled according to the posterior is available, it is possible to estimate, not only posterior model parameter covariances, but also resolution measures that are more useful in many applications. For example, posterior probabilities of the existence of interesting Earth structures like discontinuities and flow patterns can be estimated. These extended possibilities for resolution analysis may also provide new insight into problems that are usually treated by means of analytical methods.

A discussion of methodologies for nonlinear geophysical inverse problems is presented. Geophysical inverse problems are often posed as optimization problems in a finite-dimensional parameter space. An Earth model is usually described by a set of parameters representing one or more geophysical properties (e.g. the speed with which seismic waves travel through the Earth's interior). Earth models are sought by minimizing the discrepancies between observation and predictions from the model, possibly, together with some regularizing constraint. The resulting optimization problem is usually nonlinear and often highly so, which may lead to multiple minima in the misfit landscape. Global (stochastic) optimization methods have become popular in the past decade. A discussion of simulated annealing, genetic algorithms and evolutionary programming methods is presented in the geophysical context. Less attention has been paid to assessing how well constrained, or resolved, individual parameters are. Often this problem is poorly posed. A new class of method is presented which offers potential in both the optimization and the `error analysis' stage of the inversion. This approach uses concepts from the field of computational geometry. The search algorithm described here does not appear to be practical in problems with dimension much greater than 10.

The site-specific relaxation-time parametrization of relative sea level histories, for sites that were ice covered at the last glacial maximum, is herein applied in the context of formal inversions of the highest quality fraction of such data in order to infer the depth dependence of mantle viscosity. These data are jointly inverted together with additional relevant information that includes the relaxation spectrum for Fennoscandian rebound, originally derived by McConnell and two data derived from observed anomalies in the Earth's present rotational state. The latter include both the so-called `nontidal' component of the observed axial acceleration of rotation and the ongoing motion of the north pole of rotation relative to the surface geography at a rate near per million years that is directed southwards along the west meridian of longitude. The formal inversion of the totality of these data is based upon the Bayesian methodology of Tarantola and Valette, Jackson and Matsu'ura, and Backus. Both the preparation of the data that is required for the formal analysis and the derivation of the Fréchet kernels for the individual data types are discussed in some detail. The results obtained in these analyses, preliminary versions of which were recently described in abbreviated form elsewhere, appear to be rather significant. The variation of mantle viscosity with depth deduced from the glacial isostatic adjustment data is found to agree, within a constant scale factor and then rather precisely, with a model previously inferred on the basis of nonhydrostatic geoid anomalies related to the mantle convection process. Since the latter data are insensitive to a constant rescaling, this implies that the rheology of the bulk mantle may exhibit no significant transient behaviour and thus may well be Newtonian.

Thermal history modelling is a significant part of hydrocarbon exploration and resource assessment. Its primary use is to predict the volume and timing of hydrocarbon generation as a sedimentary basin evolves on timescales of - years. Forward modelling is commonly used to constrain the thermal history in sedimentary basins. Alternatively, inversion schemes may be used which have many advantages over the conventional forward modelling approach. An example of an inversion approach is presented here, wherein the preferred philosophy is to find the least complex model that fits the data. In this case, we estimate a heat flow function (of time) which provides an adequate fit to the available thermal indicator calibration data. The function is also constrained to be smooth, in either a first or second derivative sense. Extra complexity or structure is introduced into the function only where required to fit the data and the regularization stabilizes the inversion. The general formulation is presented and a real data example from the North Slope, Alaska is discussed.

The problem of integrating into a point solution gravity data and seismic data, to derive mass density and slowness of the medium is presented. A continuous approach is proposed which is already used in other fields. The general theory of modelling continuous observations through Wiener measures is presented, and the relevant optimal linear estimation problem is then solved. The integrated gravimetric-tomographic problem in two dimensions is then modelled, linearized, Fourier transformed and analytically solved. A short conclusion follows.

The problem of the reconstruction of the shape of a perfectly conducting cylinder in a cross-borehole configuration is addressed. The initial data is the harmonic electromagnetic field diffracted by the object to a receiving borehole. The method is based on an iterative conjugate gradient algorithm which requires the solving of two reciprocal direct diffraction problems at each step. These problems are investigated with a rigorous boundary integral method and finite elements. A simple and original regularization scheme is presented, which ensures the robustness of the algorithm. Numerical examples with lossy embedding media and additional random noise for both and polarizations are given.

The identification of an unknown state-dependent source term in a reaction-diffusion equation is considered. Integral identities are derived which relate changes in the source term to corresponding changes in the measured output. The identities are used to show that the measured boundary output determines the source term uniquely in an appropriate function class and to show that a source term that minimizes an output least squares functional based on this measured output must also solve the inverse problem. The set of outputs generated by polygonal source functions is shown to be dense in the set of all admissible outputs. Results from some numerical experiments are discussed.

We derive an asymptotic formula for the steady-state voltage potential in the presence of a finite number of diametrically small inhomogeneities with conductivity different from the background conductivity. We use this formula to establish continuous dependence estimates and to design an effective computational identification procedure.

In two previous papers in this journal we presented a simple method for determining the support of a scattering object from noisy far-field data for transverse magnetic polarized electromagnetic waves. This method was based on the solution of a linear integral equation of the first kind with the mathematical analysis being based on an investigation of an interior transmission problem. In this paper we consider the case of transverse electric polarized electromagnetic waves and again obtain a linear integral equation whose solution yields the support of the scattering object. The mathematical analysis in this case is based on an interior transmission problem different from the one previously considered. Numerical examples are given in the limiting case of a perfect conductor and limited aperture data.

The general quadratic Radon transform in two dimensions is investigated. Whereas the classical Radon transform of a smooth function represents the integration over all lines, the general quadratic Radon transform integrates over all conic sections. First, the parabolic isofocal Radon transform, i.e. the restriction of the general quadratic Radon transform to all parabolae with focus in the origin, is defined and illustrated. We show its intense relation to the classical Radon transform, deduce a support theorem, formulate an extension of the support theorem and derive an inversion formula. The natural extension to a more general class of isofocal quadratic Radon transforms is outlined. We show how the general quadratic Radon transform can be derived from the integrals over all parabolae by solving the related Cauchy problem. Finally, we introduce an entirely geometrical definition of a generalized Radon transform, the oriented generalized Radon transform.

In this paper tomographic reconstruction based on the concept of ridge functions (Logan and Shepp) is considered. A reconstruction approach for the ridge functions from a finite number of arbitrary projections is suggested within the framework of parallel beam geometry. The method deals with images that can be presented as a sum of ridge functions. This assumption results in a consistent linear system of Fredholm integral equations of the third kind in terms of one-dimensional functions. We derive a formula to calculate the ridge functions from the set of arbitrary projections. In the case of equally spaced projections formulae for the analytical inversion of matrices encountered in the calculation of ridge functions are derived.

In this paper, expansion formulae are constructed in terms of products of solutions of two Sturm-Liouville problems on the semi-axis, and the corresponding operators (known as -operators or recursion operators) for which the above products are eigenfunctions, are derived in an explicit form.

We consider the problem of determining a reflecting convex surface transforming the energy flow from a given point source of light into an energy flow from a prescribed-in-advance set of virtual sources. This set may consist of a finite set of point sources or of distributed sources. The problem is studied in the geometrical optics approximation. The analytic formulation of the problem leads to a complicated nonlinear partial differential equation of Monge-Ampère type. Here, we formulate the problem in terms of certain associated measures and prove the existence of weak solutions.

This paper considers an inverse problem for wave propagation in a perturbed, dissipative half-space. The perturbation is assumed to be compactly supported. This paper shows that in dimension three, the perturbation is uniquely determined by knowledge of the Dirichlet-to-Neumann map on an open subset of the boundary.

We are concerned with the retrieval of the unknown cross section of a homogeneous cylindrical obstacle embedded in a homogeneous medium and illuminated by time-harmonic electromagnetic line sources. The dielectric parameters of the obstacle and embedding materials are known and piecewise constant. That is, the shape (here, the contour) of the obstacle is sufficient for its full characterization. The inverse scattering problem is then to determine the contour from the knowledge of the scattered field measured for several locations of the sources and/or frequencies. An iterative process is implemented: given an initial contour, this contour is progressively evolved such as to minimize the residual in the data fit. This algorithm presents two main important points. The first concerns the choice of the transformation enforced on the contour. We will show that this involves the design of a velocity field whose expression only requires the resolution of an adjoint problem at each step. The second concerns the use of a level-set function in order to represent the obstacle. This level-set function will be of great use to handle in a natural way splitting or merging of obstacles along the iterative process. The evolution of this level-set is controlled by a Hamilton-Jacobi-type equation which will be solved by using an appropriate finite-difference scheme. Numerical results of inversion obtained from both noiseless and noisy synthetic data illustrate the behaviour of the algorithm for a variety of obstacles.

Three-dimensional (3D) eddy current non-destructive evaluation of steam generator tubes is cast in a wavefield integral framework and considered from an inverse problem point of view. Three inversion algorithms based on a gradient-type iterative search are studied: the modified gradient method, an inversion via the source-type integral equation, and one based on the localized nonlinear approximation. To overcome the inherent ill-posed nature of the inversion problem, a binary constraint is enforced on the contrast to be retrieved. Special attention is devoted to the evolution of the iterative processes, which is controlled by means of a tunable `cooling' parameter. The difficulty of such 3D reconstructions is discussed with emphasis on attenuation problems that are typical in eddy current analysis.

The uniqueness of determining the optical parameters of a thin film deposited upon a massive substrate from the amplitude reflection coefficient is established. The film and substrate materials are assumed to be dispersive and absorbing. The proof is performed under the assumption that the dielectric functions of the materials satisfy certain restrictions imposed by the causality principle and dispersion theories.

In this paper we study a linearized inverse reflection problem for the elastic wave equations. We derive the relation between polarization sets of reflected waves and wavefront sets of the Lamé parameters. The result does not require the `no caustics' assumption on the incident wavefront. The use of polarization sets of vector-valued distributions is crucial in our proof.

Starting from the free fermion description of the one-component KP hierarchy, we establish a connection between this approach and the theory of Darboux and binary Darboux transformations. Certain difference identities - allowing for the treatment of both continuous as well as discrete evolution equations - turn out to be crucial: first to show that any solution of the associated (adjoint) linear problems can always be expressed as a superposition of KP (adjoint) wavefunctions and then to interpret Darboux (and binary Darboux) transformations as Bäcklund transformations in the fermion language.

We develop discrete counterparts to the Gel'fand-Levitan and Marchenko integral equations for the two-dimensional (2D) discrete inverse scattering problem in polar coordinates with a nonlocal potential. We also develop fast layer stripping algorithms that solve these systems of equations exactly. The significance of these results is: (1) they are the first numerical implementation of Newton's multidimensional inverse scattering theory; (2) they show that the result will almost always be a nonlocal potential, unless the data are `miraculous'; (3) they show that layer stripping algorithms implement fast `split' signal processing fast algorithms; (4) they link 2D discrete inverse scattering with 2D discrete random field linear least-squares estimation; and (5) they formulate and solve 2D discrete Schrödinger equation inverse scattering problems in polar coordinates.

Department of Applied Mathematics, National Sun Yat-sen University, Kaohsiung, Taiwan 80424, Republic of China

Received 17 February 1998

Abstract:

We give a short proof to a key lemma in a previous paper.

The Newsletter is a key element in further enhancing the value of the journal to the inverse problems community. So why not be a part of this exciting forum by sending to our Bristol office material suitable for inclusion under any of the categories mentioned above. Your contributions will be very welcome.

Forthcoming event

Conference announcement

2nd International Conference on Identification in Engineering Systems, University of Wales Swansea, 29 - 31 March 1999

Parameter estimation and system identification are used extensively to obtain dynamic models of engineering systems. A large number of methods have been developed and a huge amount of experience gained in their application, particularly in control engineering and structural dynamics. Although aspects of the methods are different there is a substantial overlap in the methodology and practice used in the identification. Following the success of the first conference held in March 1996 in Swansea, this conference will provide a forum for researchers and practitioners in the art and science of identification from a range of disciplines and provide a further impetus to the cross-fertilization of ideas in this area. Further details, including the procedure for the submission of abstracts, are available at URL:

http://www.swan.ac.uk/mecheng/ies99/

or contact Dr M I Friswell (e-mail: m.i.friswell@swansea.ac.uk, fax: +44 (0)1792 295676).

Book reviews

75 Years of Radon Transform

S Gindikin and P Michor (ed)

1994 Boston, MA: International 303 pp ISBN 1-57146-008-X $42.00

In 1917 Johann Radon published his now celebrated formula for reconstructing a function (in many applications, this means the density of an object) from line integrals through it in different directions [1]. This paper now stands out as one of the most fundamental contributions of all time to the subject of inverse problems. It inspired much fundamental work in mathematics, such as a notable series of papers by Fritz John in the 1930s. However, the inventors of computerized tomography (CT) for medical imaging could not trace any of this when they needed exactly this inversion in the 1960s. The full significance of Radon's pioneering contribution did not become universally recognized until the 1970s.

In 1917, early on in his career, Johann Radon was an assistant and a Privatdozent at the University of Vienna. He would later spend 25 years at various German universities before finishing his career as Dean, and later Rector, at his alma mater, the University of Vienna. In 1992, the 75th anniversary of the transform was celebrated at the University of Vienna with a conference. This book forms the proceedings of that conference.

The book has three major parts:

1. Biographical contributions. This part contains, among other items, a biography written by Radon's daughter Brigitte Burkovics, reminiscences by one of his students and by Fritz John, and a description by Allen Cormack about how he approached the line-integral inversion problem when developing CT.

• Scientific contributions. This part constitutes the bulk of the book; it contains selected presentations from the technical sessions of the conference - not easy reading for the mathematically faint-hearted.

• Reprinted papers. We find here some notes by the Editor of the volume, followed by a now classical (1938) contribution by Fritz John, and the original 1917 paper by Radon.

One thing the book does not contain (in line with the mathematical theme of the conference) is any summary of how the transform - in its many forms of implementation - is now used throughout a vast array of applications.

For a general scientific audience, the first part contains fascinating historical reading, and the third part provides for pleasant casual browsing (as well as for in-depth study). The second part is strictly for specialists in the mathematical aspects of the Radon transform.

Reference

[1] Radon J 1917 Über die Bestimmung von Functionen durch ihre integralwerte längs gewisser Mannigfaltigkeiten Ber. Sächsische Akad. der Wissenschaften, Leipzig, Math.-Nat. Kl. 69 262 - 77

B Fornberg University of Colorado, Boulder

Inverse Problems of Wave Propagation and Diffraction Proceedings, Aix-les-Bains, France 1996, Lecture Notes in Physics, Volume 486

G Chavent and P C Sabatier (ed)

1997 Berlin: Springer 379 pp ISBN 3-540-62865-7 DM106.00, öS774.00, sFr96.50, £ 41.00, $79.00

This book is a collection of lectures that were presented at the `Conference on Inverse Problems of Wave Propagation and Diffraction'. This meeting was organized by two renowned French experts in inverse problems, Guy Chavent and Pierre C Sabatier, in Aix-les-Bains in September 1996.

What impressed me about this book was the clear orientation of the vast majority of the papers towards applications. The range of these applications is quite broad. In terms of fields of study, it varies from `electromagnetic' to `acoustic' inverse problems. Applications naturally dictate a broad variety of mathematical models as well as the appropriate mathematical tools. Regarding the models, the majority of authors consider the frequency domain regime, thus dealing with the Helmholz-like equation. Some authors, however, also work with the inverse problems for the hyperbolic (i.e. time dependent) equations. The goal of almost all the papers is clear and can be appreciated: to develop and test effective numerical methods for the inverse problems under consideration.

The problems studied here can mainly be split into two categories, which have rather blurry boundaries: inverse obstacle problems and inverse coefficient problems. In the first class, one is recovering the shape and location of an obstacle given scattered data. Often, this is an impenetrable obstacle. In the second class, the goal is to find an internal structure of a penetrable object, not only its shape. As a result, the second class of problems amounts to the determination of an unknown coefficient(s) of a PDE. An interesting observation is that the majority of authors discussing the inverse obstacle problems are profoundly influenced by, I would say, a classic book by D Colton and R Kress: Inverse Acoustic and Electromagnetic Scattering Theory.

A point which is made, implicitly or explicitly, in almost all the papers is the importance of reasonable a priori constraints on the solution of an inverse problem. While a wide variety of numerical approaches is discussed (given the broad scope of inverse problems under consideration), this is perhaps the only point which is common to all the approaches. This falls well into the fundamental Tikhonov's principle of an a priori choice of an appropriate compact set of solutions.

Here are some examples of these a priori constraints. The paper by D Colton describes a fresh idea to recover only support of a penetrable anomaly rather than the value of the unknown coefficient within it. In this way the original nonlinear problem is reduced to a linear one, which can be solved in an elegant way using the fact that the fundamental solution of the Helmholz-like PDE has a singularity at the source location. The paper by F Natterer represents another example of a novel and effective numerical approach which was developed using the concept of a priori constraints on solutions. An intruiging core idea of this paper is to solve a classical ill-posed Cauchy problem for the elliptic equation in a well-posed fashion, assuming a priori that the grid size should not be too small. This, in turn, leads to a rapid image reconstruction algorithm, in 3D, though only in the high frequency regime.

While the works of Colton, Natterer and some other authors consider the cases of full view illumination and measurements of the target medium, which is quite acceptable in medical imaging, other authors consider the limited view case, which adds up to the ill-posedness of the problems under consideration. This is certainly true for a number of works devoted to inverse seismic problems, which are notoriously challenging. The difficulty of these problems is clearly demonstrated in the paper by L Fatone, P Maponi, C Pignotti and F Zirilli, in which the 1D inverse problem for the 2D (in space) hyperbolic equation is studied. Probably the major challenge, even in the 1D case, consists of figuring out discontinuities of the speed 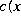) in the layered medium, given measurements of the backscattered data on the surface. Although the paper by A Litman, D Lesselier and F Santosa deals with an electromagnetic, rather than with a seismic, inverse problem, it still works with the incomplete data collection. The goal of these authors is to reconstruct the shape and location of a defect given electrical parameters of this object and incomplete view measurements of the scattered electrical field. This problem is solved by introducing a level set function which describes the shapes of a family of defects (including the correct one) and which satisfies a certain Hamilton - Jacobi-type PDE. This PDE, in turn, is connected with a least-squares cost functional.

The tutorial paper by M Bertero, P Boccacci and M Piana stays somewhat outside of the common scope of the other papers. Nevertheless, this is a very interesting work. It clarifies a rather ambiguous issue of the achievable resolution R versus the wavelength . The common view is that . The authors show, however, that this is true only in the far-field data. Contrary to this, in the case of the near-field data, resolution can be very much less than the wavelength, because of the evanescent waves, whose intensity decays exponentially with the distance from the source.

It is impossible for me to comment on all the papers included in this book. My overall comment, however, is that each of the works presented in this book is interesting in its own right, and I enjoyed reading all of them, thanks to the contributors and the editors. In my opinion, this book represents a state of the art (as of 1996) collection of numerical and some theoretical approaches to inverse problems of wave propagation.

M V Klibanov University of North Carolina, Charlotte

Inverse Nodal Problems: Finding the Potential from Nodal Lines Memoirs of the American Mathematical Society, Number 572

O H Hald and J R McLaughlin

1996 Providence, RI: American Mathematical Society 148 pp ISBN 0-8218-0486-3 £ 30.00

This book describes new and sometimes unexpected properties of an eigenvalue problem for an elliptic equation, in potential form, on a rectangle with Dirichlet boundary conditions. First the Sturm - Liouville problem for a Laplacian is considered, and eigenvalues (and thus eigenfunctions) can be easily found. The authors studied the behaviour of eigenvalues and proved that for most rectangles almost all eigenvalues are separated from other eigenvalues by a specified gap; they also found other useful features.

Next the authors describe properties of the same problem with a sufficiently smooth potential function, using perturbation theory. The main result is the proof that the potential is uniquely determined, up to an additive constant, by a subset of the nodal lines of the eigenfunctions. The authors present a formula that yields an approximation to the potential at a dense set of points.

The book is interesting to read; it could be recommended to all specialists in mathematical physics and inverse problems.

A Yagola Moscow State University

Formulas in Inverse and Ill-Posed Problems

Yu E Anikonov

1997 Utrecht: VSP 240 pp ISBN 90-6764-216-9 £ 82.00

The rather unusual title of this book is actually quite apt; it is a collection of representation formulae for a wide variety of inverse problems, but primarily those of evolution type.

Lest the reader assume that the holy grail has at last been found, I should point out that not all of the formulae give explicit representations; indeed for most of the inverse problems that are inherently nonlinear the representation is an implicit one. Also, many of the problems are not one of the standards one finds in the current literature or motivated by practical considerations (at least as far as the reviewer is aware). The book's first example is illustative: to recover the coefficient in the parabolic equation , given an initial condition 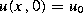and boundary values on 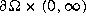. The overposed data considered are the values of the Fourier transform 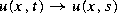, 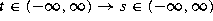for each . While this allows the coefficient to be (formally) recovered, it is not the sort of data that one expects to provide in diffusion problems.

Despite this, the book is a mine of information and useful ideas. It would certainly repay anyone interested in a particular inverse problem to examine it. It is not a book one reads but one that is consulted with the understanding that, while it will very likely not contain ready-made answers, there is reasonable hope that it might provide some insight. Proofs of the claims and justification of the formulae are rarely complete, but there is an extensive list of references, although these are certainly not representative of the areas claimed to be covered in the text. To amplify the last remark, more than two thirds of the citations are to the Russian literature; half of these are by the book's author. Of the remaining third, half are to books or articles published before 1975 and only 20% to works of the last ten years. Thus the recent explosion in the inverse problems literature on a worldwide basis over the last decade or so is largely unaddressed.

Who will or should buy this book? As the above remarks indicate, it is not really suitable as a textbook for graduate courses, at least not for programmes in western Europe or the USA. I suspect that the market here is the research libraries, as I don't imagine many individuals will find it to be a must-have item for their bookshelves, and the very high cost per page will not help in this regard.

W Rundell Texas A&M University, College Station

Inverse Problems in Wave Propagation The IMA Volumes in Mathematics and its Applications, Volume 90

G Chavent, G Papanicolaou, P Sacks and W Symes (ed)

1997 Berlin: Springer 498 pp ISBN 0-387-94976-3 DM118.00, öS861.40, sFr104.00, £ 48.50, $96.95

This book is based on the proceedings of a two-week workshop which was an integral part of the 1994 - 1995 IMA programme `Waves and Scattering'. This workshop took place from 6 - 17 March 1995. There are 24 papers. This book represents most applications in inverse wave propagation problems, together with fundamental mathematical investigations of the relation between waves and scatterers. The following contributions are included.

R A Albanese discusses wave propagation issues in medicine and environmental health. The uniqueness of one-dimensional reconstruction for orthogonal and oblique incidence is touched upon. J G Berryman shows that the inverse problem with the data serving as constraints is most easily analysed when it is possible to segment the solution space into regions that are feasible (satisfying all the constraints) and infeasible (violating some of the constraints). The variational structure of three inverse problems has been investigated. R W Brookes and K P Bube investigate the numerical convergence of a finite-difference method in space and time for one-dimensional models in reflection seismology, and discuss the order of convergence in relation to the source wavelet. M D Collins discusses topics in ocean acoustic inverse problems, including remote sensing and localization problems. Efficient techniques are discussed for the solution of the forward problem, including poro-elastic media, and techniques for solving global scale acoustic problems have been adapted. D Colton discusses in general the three-dimensional electromagnetic inverse scattering problem for inhomogeneous objects and in particular an example in medical imaging. A two-dimensional problem is solved numerically with the dual space method. E Croc and Y Dermenjian study the generalized modes in an acoustic strip, which is a simplified model of a seismic experiment, where both source and receiver are situated in a well. G Eskin and J Ralston consider the inverse problems for Schrödinger operators with magnetic and electric potentials. A Faridani shows old and new results in computed tomography, which entails the reconstruction of a function f from line integrals off. Problems of uniqueness, reconstruction formulae for the x-ray transform, filtered backprojection, error estimates and incomplete data problems are treated in detail. D J Foster, R G Keys and D P Schmitt propose a theoretical basis for interpreting amplitude versus offset (AVO) inversion. It defines the background seismic response and characterizes anomalous events by distance from this background. F A Grunbaum and S K Patch investigate how many parameters one can solve for in diffuse tomography. Some bounds of the range of the parameters are given. J G Harris constructs some physically reasonable models of acoustic imaging. In particular, to investigate small surface-breaking cracks, the leaky Rayleigh wave is used in the imaging mechanism. V Isakov analyses the reconstruction of the diffusion and of the principal coefficient of a hyperbolic equation, in particular the diffusion coefficient, by the use of beam solutions and the recovery of discontinuity of the wave speed. V G Khajdukov, V I Kostin and V A Tcheverda consider the r-solution and its applications in a linearized waveform inversion for a layered background. Y Kurylev and A Starkov deal with an inverse boundary problem for a second-order elliptic operator and its nonstationary counterparts. The uniqueness of the reconstruction of a density parameter is proved and a direct procedure of its reconstruction using directional moments is described. Ching-Ju Ashraf Lee and J R McLaughlin solve an inverse nodal problem for a rectangular membrane using the ratio method and the method of parameter identification. Changmei Liu derives a uniqueness theorem for any ball and for two balls, when the scattering amplitudes for some independent incident directions are given. J R McLaughlin, P E Sacks and M Somasundaram discuss the inverse problem of the determination of acoustic parameters using far-field data, by using the properties of the interior eigenvalues, and show how the sound speed depending on the vertical coordinate can be determined. G Hanamura and G Uhlmann describe a layer stripping algorithm in elastic impedance tomography, in which an elastic tensor has to be reconstructed from measurements of the displacement and the traction at the boundary of the domain. G Nolet uses the WKBJ or path integral approximation to the solution of the elastodynamic equations in a slightly heterogeneous earth to partition the inverse problem for a large set of observed seismograms along different wavepaths. R L Nowack discusses an inverse method for the analysis of refraction and wide-angle seismic data and illustrates it through the inversion of a shallow crustal structure. F R Pijpers presents a brief overview of applications of inversions within astronomy, including a recent modification of the Backus and Gilbert method. E L Ritman, J H Dunsmuir, A Faridani, D V Finch, K T Smith and P J Thomas present an example in which local reconstruction extends the capability of a micro-CT scanner beyond the physical limits imposed by global tomographic reconstruction techniques. J Sylvester discusses the layer stripping problem. Some theorems are cited as evidence that it provides a productive theoretical method which yields new insights into an old problem. M E Taylor studies estimates for approximate solutions to acoustic inverse scattering problems, in particular the recovery of the near-field wave from the scattering amplitude and the consequences of linearization of the inverse problems.

This book is certainly an important contribution to the theory and application of inverse wave propagation problems and is a good reference work that should be present in the library.

P M van den Berg Delft University of Technology