Abstract
The pattern evolution of the stripe-like  domain structure in tetragonal ferroelectric thin films upon introduction of square void arrays is investigated using Monte Carlo simulation based on the Landau-Devonshire phenomenological theory. The regular splitting of the stripe-like domains near the voids and substantial release of both the dipole-dipole interaction and the electromechanical energy are revealed. Consequently, a significant enhancement of piezoelectric coefficient
domain structure in tetragonal ferroelectric thin films upon introduction of square void arrays is investigated using Monte Carlo simulation based on the Landau-Devonshire phenomenological theory. The regular splitting of the stripe-like domains near the voids and substantial release of both the dipole-dipole interaction and the electromechanical energy are revealed. Consequently, a significant enhancement of piezoelectric coefficient  is predicted. It is suggested that the delicate balance between the two energy terms modulated by the void array periodicity and void size is responsible for the domain splitting. The present work proposes an alternative promising approach to tune the domain structure via simple micro-fabrication techniques.
is predicted. It is suggested that the delicate balance between the two energy terms modulated by the void array periodicity and void size is responsible for the domain splitting. The present work proposes an alternative promising approach to tune the domain structure via simple micro-fabrication techniques.
Export citation and abstract BibTeX RIS
The performances of ferroelectric (FE) thin films and nano-structures have been receiving considerable interest not only due to the significance in fundamental researches but also for their diverse applications in piezoelectric micro-systems, FE memories, high-frequency electronic components, etc. [1–3]. Those applications rely substantially on the FE polarization and electromechanical (piezoelectric) behaviors, which are related to the FE domain structures and their responses to different environmental stimuli such as electrical field, stress, spatial confinement (dimensionality), etc. Along this line, extensive investigations on the FE domain structure and its control in order to optimize these properties have been reported [4–6]. The so-called domain engineering on ferroelectrics has become of high concern in recent years since those application performances can be then remarkably improved [7,8].
The most representative class of FE materials targeting such applications includes FE perovskite oxides like  and
and  which have tetragonal FE phase originating from cubic paraelectric phase upon decreasing temperature T [9,10]. For a FE system like
which have tetragonal FE phase originating from cubic paraelectric phase upon decreasing temperature T [9,10]. For a FE system like  , the well-aligned stripe-like
, the well-aligned stripe-like  domain structure is one of the core characteristics [9]. For the sake of simplification, we discuss a two-dimensional (2D) FE lattice as an approach to FE thin film, where the FE polarizations are confined onto the xy-plane along the [01] and [10] easy axes. This
domain structure is one of the core characteristics [9]. For the sake of simplification, we discuss a two-dimensional (2D) FE lattice as an approach to FE thin film, where the FE polarizations are confined onto the xy-plane along the [01] and [10] easy axes. This  domain structure is the consequence of the delicate balance mainly between the electric dipole-dipole interactions (depolarization effect) associated with the FE polarization and the electromechanical (elastic plus electrostrictive) energy associated with the piezoelectricity and electrostriction effect, while the domain wall energy may not be negligible, too [11]. This delicate balance is the reason for sensitive responses of the domain structure to either external electric field or stress/pressure, so as to exhibit excellent electromechanical performances in addition to the favored FE properties [12].
domain structure is the consequence of the delicate balance mainly between the electric dipole-dipole interactions (depolarization effect) associated with the FE polarization and the electromechanical (elastic plus electrostrictive) energy associated with the piezoelectricity and electrostriction effect, while the domain wall energy may not be negligible, too [11]. This delicate balance is the reason for sensitive responses of the domain structure to either external electric field or stress/pressure, so as to exhibit excellent electromechanical performances in addition to the favored FE properties [12].
It is noted that both the dipole-dipole interactions and the electromechanical energy in a FE lattice are long-ranged and they can be strongly modulated by imposing various spatial constraints, in particular the dimensionality and geometric constraints. They are responsible for very scattered FE and piezoelectric properties of finite-size FE materials such as nano- or micro-scale dots and islands as well as substrates confined thin films [13–15]. Consequently, the regular stripe-like or twinned  domain structure in bulk lattice may be replaced by vortex-like domain pattern and others. Quite a number of works reported observations of various fascinating domain patterns by modulating these spatial constraints [16,17]. Taking a naked FE island (in-plane size L and thickness D, and
domain structure in bulk lattice may be replaced by vortex-like domain pattern and others. Quite a number of works reported observations of various fascinating domain patterns by modulating these spatial constraints [16,17]. Taking a naked FE island (in-plane size L and thickness D, and  for thin films) with free boundary as an example, one can easily predict the evolution of domain structure, with decreasing L from stripe-like domain pattern into a coexistence of the stripe-like pattern and the vertex-like one, eventually into a single vertex pattern [18]. For such small-size island, the dipole-dipole interaction in competing with the electromechanical energy dominates the formation of vertex structure. It was reported that such FE islands in some cases do exhibit better electromechanical performances than their bulk counterpart.
for thin films) with free boundary as an example, one can easily predict the evolution of domain structure, with decreasing L from stripe-like domain pattern into a coexistence of the stripe-like pattern and the vertex-like one, eventually into a single vertex pattern [18]. For such small-size island, the dipole-dipole interaction in competing with the electromechanical energy dominates the formation of vertex structure. It was reported that such FE islands in some cases do exhibit better electromechanical performances than their bulk counterpart.
Given the rapid progress in micro-fabrication technology of materials, one may have additional approaches to engineer the FE domain structure. While a fabrication of well-aligned FE island lattices (arrays) faces technical challenging, it represents one end of releasing the spatial constraints. In this case, the dipole-dipole interaction and electromechanical energy are seriously released. The other end would be an alternative scheme in which an infinite FE thin film can be patterned by removing finite-size units, so that a grid thin film structure with periodically aligned voids (void array) can be fabricated. This end scheme seems quite less touched in the literature so far but offers several particulars. Starting from a stripe-like  domain structure, fabricating such voids would result in several consequences. First, the thin film as a whole remains continuous, but the voids will partially release the electromechanical energy of the neighboring film region while the dipole-dipole interaction enforces the electric polarizations surrounding the voids to re-align. By properly designing the spatial distribution, shape, and size of the voids, one is allowed to modulate substantially the stripe-like domain pattern for specific purposes. Second, due to the high mobility of the
domain structure, fabricating such voids would result in several consequences. First, the thin film as a whole remains continuous, but the voids will partially release the electromechanical energy of the neighboring film region while the dipole-dipole interaction enforces the electric polarizations surrounding the voids to re-align. By properly designing the spatial distribution, shape, and size of the voids, one is allowed to modulate substantially the stripe-like domain pattern for specific purposes. Second, due to the high mobility of the  domain walls, such voids may benefit to the enhancement of the FE and electromechanical responses. Third, with respect to the FE island array, this grid thin film structure can be easily and efficiently fabricated by up-bottom fabrication techniques, which is technologically favored and cost-competitive.
domain walls, such voids may benefit to the enhancement of the FE and electromechanical responses. Third, with respect to the FE island array, this grid thin film structure can be easily and efficiently fabricated by up-bottom fabrication techniques, which is technologically favored and cost-competitive.
In this work, we investigate the spatial evolution of the  domain structure in a FE thin film with periodically aligned square void array, based on the well-known Landau-Devonshire phenomenological theory [19–22]. Certainly, the shape of voids can be other than square but the underlying physics should be similar. We start from a 2D
domain structure in a FE thin film with periodically aligned square void array, based on the well-known Landau-Devonshire phenomenological theory [19–22]. Certainly, the shape of voids can be other than square but the underlying physics should be similar. We start from a 2D  square lattice with periodic boundary conditions as an approach to an infinite FE thin film. On each site i two order parameters are imposed: polarization vector
square lattice with periodic boundary conditions as an approach to an infinite FE thin film. On each site i two order parameters are imposed: polarization vector  ,
,  and displacement vector
and displacement vector  ,
,  , where x and y are the coordinate axes. Following earlier literature, the free energy of the FE lattice includes the Landau energy, gradient energy, dipole-dipole interaction, elastic energy, electrostrictive interaction, and electrostatic energy [18]. For such a lattice, the total free energy density can be written as
, where x and y are the coordinate axes. Following earlier literature, the free energy of the FE lattice includes the Landau energy, gradient energy, dipole-dipole interaction, elastic energy, electrostrictive interaction, and electrostatic energy [18]. For such a lattice, the total free energy density can be written as
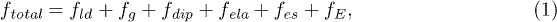
where the terms  ,
,  ,
,  ,
,  ,
,  ,
,  are the Landau energy, gradient energy, dipole-dipole interaction, elastic energy, electrostrictive energy, and electrostatic energy, respectively. The electromechanical energy includes
are the Landau energy, gradient energy, dipole-dipole interaction, elastic energy, electrostrictive energy, and electrostatic energy, respectively. The electromechanical energy includes  plus
plus  . The Landau energy is a polynomial extended to the sixth order:
. The Landau energy is a polynomial extended to the sixth order:
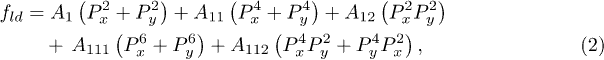
where A with various subscripts are the Landau coefficients. Usually,  is T-dependent and can be written as
is T-dependent and can be written as  , where
, where  is the critical point for the FE transition, and
is the critical point for the FE transition, and  with vacuum permittivity
with vacuum permittivity  and Curie constant C. Positive
and Curie constant C. Positive  and negative
and negative  are required for the FE transitions. The domain wall energy is expressed by the gradient energy form:
are required for the FE transitions. The domain wall energy is expressed by the gradient energy form:
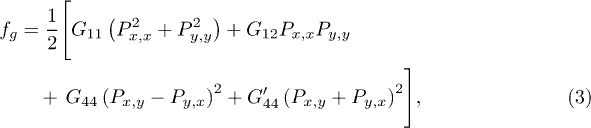
where  , and
, and  are the gradient energy coefficients. The long-range electric dipole-dipole interaction is written as
are the gradient energy coefficients. The long-range electric dipole-dipole interaction is written as

where the pre-factor  is taken for normalizing purpose. We can re-write eq. (4) as
is taken for normalizing purpose. We can re-write eq. (4) as

where the internal electric field  is
is
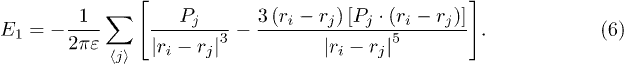
Due to the existence of voids in the lattice, big lattice size L has to be taken. A precise account of this long-range term using the Ewald summation scheme becomes practically overtedious [23]. Fortunately, for 2D lattice, one can choose a preset truncating distance  from the central site in order make the computation tractable. This scheme is sufficient for a reliable account of this interaction (
from the central site in order make the computation tractable. This scheme is sufficient for a reliable account of this interaction ( in our simulation) [24,25].
in our simulation) [24,25].
Subsequently, the elastic energy reads
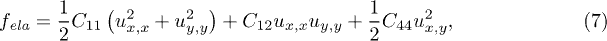
where  ,
,  , and
, and  are the elastic coefficients. The electrostrictive energy accounting the coupling between the polarization field and strain field is written as
are the elastic coefficients. The electrostrictive energy accounting the coupling between the polarization field and strain field is written as
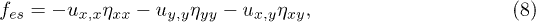
with strain  ,
,  and
and  , where
, where  are the electrostrictive coefficients. Finally, the electrostatic energy is
are the electrostrictive coefficients. Finally, the electrostatic energy is

with applied electric field  .
.
The void array is simply introduced into the FE lattice by imposing  and
and  in the pre-designed regions. Here we only consider square voids with the two sides aligning along the x-axis and y-axis, respectively. It is noted that these voids in the lattice makes it mathematically challenging to properly handle the mechanical balance conditions on the boundaries between thin film matrix and voids. This difficulty becomes particularly clear if the time-dependent Ginzburg-Landau equation (TDGL, Langevin-type) is used to solve this issue numerically [16]. However, no such difficulty appears if one employs the Monte Carlo (MC) simulation to track the evolution of the FE lattice [18]. A reasonable assumption here is that the response time of elastic strain is far shorter than that for dipole relaxation, such that the mechanical equilibrium is instantly established when an electric dipole flip event occurs [15,26]. The object lattice of our simulation is
in the pre-designed regions. Here we only consider square voids with the two sides aligning along the x-axis and y-axis, respectively. It is noted that these voids in the lattice makes it mathematically challenging to properly handle the mechanical balance conditions on the boundaries between thin film matrix and voids. This difficulty becomes particularly clear if the time-dependent Ginzburg-Landau equation (TDGL, Langevin-type) is used to solve this issue numerically [16]. However, no such difficulty appears if one employs the Monte Carlo (MC) simulation to track the evolution of the FE lattice [18]. A reasonable assumption here is that the response time of elastic strain is far shorter than that for dipole relaxation, such that the mechanical equilibrium is instantly established when an electric dipole flip event occurs [15,26]. The object lattice of our simulation is  thin film. The relevant materials parameters are taken from the literature [18]. We assume that the lattice constant
thin film. The relevant materials parameters are taken from the literature [18]. We assume that the lattice constant  , Landau coefficient
, Landau coefficient  , and polarization
, and polarization  at
at  far below
far below  are known as reference, where
are known as reference, where  and
and  . All the free energy terms are normalized by term
. All the free energy terms are normalized by term  which has an energy unit [27]. Table 1 lists the chosen parameters for simulation.
which has an energy unit [27]. Table 1 lists the chosen parameters for simulation.
Table 1:.
Parameters chosen for the simulation ( , Boltzmann constant
, Boltzmann constant  ).
).
| Parameter (unit) | Value | Parameter (unit) | Value | Parameter (unit) | Value |
|---|---|---|---|---|---|
 |
0.10 |  |
−0.24 |  |
4.50 |
 |
0.49 |  |
1.20 |  |
1.60 |
 |
0.00 |  |
0.80 |  |
0.80 |
 |
2.75 |  |
1.79 |  |
0.54 |
 |
0.142 |  |
−0.0074 |  |
0.0157 |
 |
64 |  |
5.00 |
For practical simulation, we submit a FE lattice free of any void to a high  for annealing. Then the lattice is gradually cooled with sufficient relaxation time down to a low
for annealing. Then the lattice is gradually cooled with sufficient relaxation time down to a low  . The details of the simulation were reported in our earlier work [24,25] and no description is given here. Figure 1(a) shows the simulated
. The details of the simulation were reported in our earlier work [24,25] and no description is given here. Figure 1(a) shows the simulated  domain structure with L = 64. The well-aligned stripe-like
domain structure with L = 64. The well-aligned stripe-like  domain walls along the
domain walls along the ![$[1\bar{1}]$](https://content.cld.iop.org/journals/0295-5075/108/2/27009/revision1/epl16612ieqn84.gif) direction are observed. The results are well consistent with phase-field simulations using the TDGL equation [15,26,28]. Subsequently, a periodically distributed square void array of given size
direction are observed. The results are well consistent with phase-field simulations using the TDGL equation [15,26,28]. Subsequently, a periodically distributed square void array of given size  is introduced into the lattice and a sufficiently long-time relaxation of the domain structure is allowed. The eventually reached domain structure as the energy lowest state (the ground state) is checked carefully by choosing various annealing paths.
is introduced into the lattice and a sufficiently long-time relaxation of the domain structure is allowed. The eventually reached domain structure as the energy lowest state (the ground state) is checked carefully by choosing various annealing paths.
Fig. 1: (Color online) Simulated in-plane domain patterns for  (a), 4 (b), 6 (c), and 12 (d), respectively. The arrows indicate the domain polarization orientation which is defined by angle θ.
(a), 4 (b), 6 (c), and 12 (d), respectively. The arrows indicate the domain polarization orientation which is defined by angle θ.
Download figure:
Standard imageWe perform extensive simulations via the standard Metropolis algorithm on the domain structure evolution by imposing different spatial distribution and size of the voids. It is shown that the evolutions share qualitatively similar characteristics. As an example, we present in figs. 1(b)–(d) the simulated domain structures with a  void array, forming a grid FE thin film. The void size
void array, forming a grid FE thin film. The void size  takes 0, 4, 6, and 12, respectively. At the first glance, the existence of voids in the FE thin film has marked impact on the domain structure. However, differently from FE islands where the vertex pattern is preferred, we observe an interesting pattern evolution when
takes 0, 4, 6, and 12, respectively. At the first glance, the existence of voids in the FE thin film has marked impact on the domain structure. However, differently from FE islands where the vertex pattern is preferred, we observe an interesting pattern evolution when  takes different values. At
takes different values. At  , the well-aligned
, the well-aligned  domain structure with straight walls (fig. 1(a)) can be maintained roughly, whereas only local deformation in the domain walls neighboring the void boundaries is seen, as shown in fig. 1(b). This local deformation becomes complicated as
domain structure with straight walls (fig. 1(a)) can be maintained roughly, whereas only local deformation in the domain walls neighboring the void boundaries is seen, as shown in fig. 1(b). This local deformation becomes complicated as  and the pattern at
and the pattern at  is shown in fig. 1(c). Surprisingly, regular domain splitting sequence is clearly observed due to the introduction of the void array. By such splitting, one can halve the domain width and periodicity. This domain splitting can sustain until
is shown in fig. 1(c). Surprisingly, regular domain splitting sequence is clearly observed due to the introduction of the void array. By such splitting, one can halve the domain width and periodicity. This domain splitting can sustain until  is big enough, such as
is big enough, such as  , as shown in fig. 1(d), where the FE lattice consists of crossing thin grids along the x-axis and y-axis. Due to the strong depolarization effect, all the domains in the horizontal grid edges align along the x-axis and those in the vertical grid edges align along the y-axis. However, every edge-crossing region is occupied by local
, as shown in fig. 1(d), where the FE lattice consists of crossing thin grids along the x-axis and y-axis. Due to the strong depolarization effect, all the domains in the horizontal grid edges align along the x-axis and those in the vertical grid edges align along the y-axis. However, every edge-crossing region is occupied by local  domain structure (two
domain structure (two  walls).
walls).
It seems that for the grid FE lattice, the domain walls favor the self-adaptive evolution so that the electric polarizations neighboring the voids can align in parallel to the boundary rather than any other choice. This is a common feature almost applicable for all the cases. It is found that the domain splitting sequence can be realized by properly assigning the void array periodicity  and void size
and void size  in a broad range, thus a flexible and easily accessed approach to control the domain structure is obtained. In comparison with FE islands, the grid FE lattice seems to offer rich possibilities of domain patterns [17].
in a broad range, thus a flexible and easily accessed approach to control the domain structure is obtained. In comparison with FE islands, the grid FE lattice seems to offer rich possibilities of domain patterns [17].
In order to see more clearly the domain splitting, we choose the case of the  void array and
void array and  for an illustration. The snapshoted domain patterns at four annealing times
for an illustration. The snapshoted domain patterns at four annealing times  are shown in figs. 2(a)–(d). Starting from the initial state in fig. 2(a), each stripe-like domain with vertical polarization begins to split at positions near the voids and generates two branches, as shown in fig. 2(b). The splitting develops continuously with time along the
are shown in figs. 2(a)–(d). Starting from the initial state in fig. 2(a), each stripe-like domain with vertical polarization begins to split at positions near the voids and generates two branches, as shown in fig. 2(b). The splitting develops continuously with time along the  direction and ends near the neighboring void. This sequence thus generates the final well-aligned and regularly split domain structure shown in fig. 2(d) and fig. 1(d).
direction and ends near the neighboring void. This sequence thus generates the final well-aligned and regularly split domain structure shown in fig. 2(d) and fig. 1(d).
Fig. 2: (Color online) Instantly snapshoted domain patterns upon thermal annealing at  for various times t = 0 (a),
for various times t = 0 (a),  (b),
(b),  (c), and
(c), and  (d) for a FE lattice with
(d) for a FE lattice with  void array and
void array and  . The Fourier spectra of the spatial correlation function for the FE lattices in (a) and (d) are plotted in (f) and (g), respectively. The Fourier spectrum of the lattice free of any void is shown in (e) for comparison. The arrows in (e)–(g) indicate the spots from the domain structures.
. The Fourier spectra of the spatial correlation function for the FE lattices in (a) and (d) are plotted in (f) and (g), respectively. The Fourier spectrum of the lattice free of any void is shown in (e) for comparison. The arrows in (e)–(g) indicate the spots from the domain structures.
Download figure:
Standard imageConsidering the well-organized split domain structures, we also consult the Fourier transform spectrum of the dipole correlation function in the wave vector  space. The Fourier spectrum of the spatial correlation function is defined as
space. The Fourier spectrum of the spatial correlation function is defined as
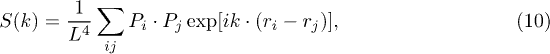
where subscripts i and j denote the lattice sites. Figures 2(e)–(g) show, respectively, the Fourier spectra of the FE lattice free of void (fig. 1(a)), the FE lattices with  void array and
void array and  without any annealing and with sufficient annealing. A comparison of figs. 2(a) and (b) helps us to identify the indications of the spots. The bright spot at
without any annealing and with sufficient annealing. A comparison of figs. 2(a) and (b) helps us to identify the indications of the spots. The bright spot at  , as indicated by the arrow in fig. 2(e), reflects the stripe domain pattern whereas the weaker spot at
, as indicated by the arrow in fig. 2(e), reflects the stripe domain pattern whereas the weaker spot at  comes from the high-order effect from the Fourier transform. The additional dim spots in fig. 2(f) obviously come from the
comes from the high-order effect from the Fourier transform. The additional dim spots in fig. 2(f) obviously come from the  void array of
void array of  , noting that the brightest spot is at
, noting that the brightest spot is at  from the stripe domain pattern. Figure 2(g) plots the Fourier spectrum of the well-developed domain pattern after the sufficient annealing. The brightest spot at
from the stripe domain pattern. Figure 2(g) plots the Fourier spectrum of the well-developed domain pattern after the sufficient annealing. The brightest spot at  characterizes the well-split stripe domain pattern. This spot originates from the shifting of the brightest spot in fig. 2(f), due to the splitting of the stripe domains.
characterizes the well-split stripe domain pattern. This spot originates from the shifting of the brightest spot in fig. 2(f), due to the splitting of the stripe domains.
To understand the physics underlying such domain splitting behaviors, one may evaluate the spatial contours of the dipole-dipole interaction  and electromechanical energy
and electromechanical energy  . For convenience of comparison, figs. 3(a) and (b) show the spatial contours of
. For convenience of comparison, figs. 3(a) and (b) show the spatial contours of  around one void of
around one void of  at annealing time t = 0 and
at annealing time t = 0 and  , respectively. It is clearly shown that those polarizations perpendicular to the void surfaces at t = 0 re-align themselves to be parallel to the surfaces during the annealing, resulting in a significant reduction of the local
, respectively. It is clearly shown that those polarizations perpendicular to the void surfaces at t = 0 re-align themselves to be parallel to the surfaces during the annealing, resulting in a significant reduction of the local  , which is one of the driving forces for the domain splitting. This process can also be illustrated by the spatial contours of the internal electric field. Figures 3(c) and (d) present the spatial contours of the magnitude of the internal electric field
, which is one of the driving forces for the domain splitting. This process can also be illustrated by the spatial contours of the internal electric field. Figures 3(c) and (d) present the spatial contours of the magnitude of the internal electric field  at t = 0 and
at t = 0 and  , with the arrows indicating the distributions of
, with the arrows indicating the distributions of  . At the up and left boundaries of voids, the dipole-dipole fields are initially offset by the strong depolarization field. The total internal field in this region is relatively small, as shown in fig. 3(c). The annealing process drives the dipoles to realign in parallel to the voids boundaries, leading to the modulated internal electric field, as shown in fig. 3(d) in comparison with fig. 3(c), focusing on the void-field boundaries. Figures 3(e) and (f) present the spatial contours of
. At the up and left boundaries of voids, the dipole-dipole fields are initially offset by the strong depolarization field. The total internal field in this region is relatively small, as shown in fig. 3(c). The annealing process drives the dipoles to realign in parallel to the voids boundaries, leading to the modulated internal electric field, as shown in fig. 3(d) in comparison with fig. 3(c), focusing on the void-field boundaries. Figures 3(e) and (f) present the spatial contours of  . Similar behaviors are observed and the existence of voids releases remarkably the local electromechanical energy. In particular, the high
. Similar behaviors are observed and the existence of voids releases remarkably the local electromechanical energy. In particular, the high  energy on those domain walls (red color) in fig. 3(e) is fully released, and the whole region has much lower
energy on those domain walls (red color) in fig. 3(e) is fully released, and the whole region has much lower  energy via the polarization re-alignment. It is noted that the total gain in the electromechanical energy and dipole-dipole interaction is much greater than the cost for additional domain walls arising from the domain splitting. Therefore, the domain splitting is thermodynamically spontaneous. It should be mentioned that those energy terms in eq. (1) other than
energy via the polarization re-alignment. It is noted that the total gain in the electromechanical energy and dipole-dipole interaction is much greater than the cost for additional domain walls arising from the domain splitting. Therefore, the domain splitting is thermodynamically spontaneous. It should be mentioned that those energy terms in eq. (1) other than  and
and  may change too upon the domain splitting. However, these changes are much less remarkable than
may change too upon the domain splitting. However, these changes are much less remarkable than  and
and  .
.
Fig. 3: (Color online) Simulated energy contours for the dipole-dipole interaction  ((a), (b)), magnitude contours of the internal electric field
((a), (b)), magnitude contours of the internal electric field  ((c), (d)), and the electromechanical energy
((c), (d)), and the electromechanical energy  ((e), (f)), at two annealing times t = 0 and
((e), (f)), at two annealing times t = 0 and  , respectively.
, respectively.
Download figure:
Standard imageOne of the favored consequences of the domain splitting is the expected enhancement of the electromechanical performance. To confirm this prediction, we evaluate the piezoelectric coefficient  defined as
defined as ![$d_{33}=\text{d} \eta^{[10]}/\text{d} E^{[10]}$](https://content.cld.iop.org/journals/0295-5075/108/2/27009/revision1/epl16612ieqn148.gif) where
where ![$\eta^{[10]}= \langle\eta_{xx}\rangle=\langle Q_{11}P_{x}^{2}+ Q_{12}P_{y}^{2}\rangle$](https://content.cld.iop.org/journals/0295-5075/108/2/27009/revision1/epl16612ieqn149.gif) ,
, ![$E^{[10]}$](https://content.cld.iop.org/journals/0295-5075/108/2/27009/revision1/epl16612ieqn150.gif) denotes the electric field along the x-axis, and
denotes the electric field along the x-axis, and  represents the configuration average [28]. When the averaging is made over the whole lattice including the voids, the evaluated piezoelectric coefficient is denoted by
represents the configuration average [28]. When the averaging is made over the whole lattice including the voids, the evaluated piezoelectric coefficient is denoted by  , while the coefficient is denoted by
, while the coefficient is denoted by  if the averaging is made over the lattice excluding the voids. We take
if the averaging is made over the lattice excluding the voids. We take ![$-0.2<E^{[10]}<0.2$](https://content.cld.iop.org/journals/0295-5075/108/2/27009/revision1/epl16612ieqn154.gif) , within which term
, within which term ![$\eta^{[10]}$](https://content.cld.iop.org/journals/0295-5075/108/2/27009/revision1/epl16612ieqn155.gif) exhibits good linear dependence on
exhibits good linear dependence on ![$E^{[10]}$](https://content.cld.iop.org/journals/0295-5075/108/2/27009/revision1/epl16612ieqn156.gif) . The evaluated
. The evaluated  and
and  as a function of
as a function of  , respectively, are plotted in fig. 4(a). One observes that both
, respectively, are plotted in fig. 4(a). One observes that both  and
and  increase rapidly with increasing
increase rapidly with increasing  and reach the maximal as
and reach the maximal as  . Afterwards, both
. Afterwards, both  and
and  begin to fall and become low as
begin to fall and become low as  is over 12. It is noted that more than 20 times enhancement in
is over 12. It is noted that more than 20 times enhancement in  is obtained as
is obtained as  increases from zero to
increases from zero to  . This implies that the introduction of the void array allows a remarkably enhanced piezoelectric coefficient, a surprising but highly favored effect.
. This implies that the introduction of the void array allows a remarkably enhanced piezoelectric coefficient, a surprising but highly favored effect.
Fig. 4: (Color online) (a) Simulated longitudinal piezoelectric coefficient  and its effective value
and its effective value  , as a function of
, as a function of  respectively for the lattice with
respectively for the lattice with  void array. The
void array. The  contours for
contours for  and
and  are shown in (b) and (c), respectively.
are shown in (b) and (c), respectively.
Download figure:
Standard imageTo find the correlation of this piezoelectric enhancement with the domain structure, one plots the spatial contours of the local  for the lattices of
for the lattices of  and
and  in figs. 4(b) and (c), respectively, where the shadowed stripes roughly mark the domain walls. As shown in figs. 3(a) and (c), the stripe-like
in figs. 4(b) and (c), respectively, where the shadowed stripes roughly mark the domain walls. As shown in figs. 3(a) and (c), the stripe-like  domain structure free of any void has both the high dipole-dipole interaction
domain structure free of any void has both the high dipole-dipole interaction  and the high electromechanical energy
and the high electromechanical energy  . In particular, the high
. In particular, the high  implies that the whole lattice is in the seriously strained state. Therefore, additional lattice deformation becomes highly resistive, i.e.
implies that the whole lattice is in the seriously strained state. Therefore, additional lattice deformation becomes highly resistive, i.e.  is very small. As expected, the
is very small. As expected, the  contour for
contour for  is roughly homogeneous over the whole lattice with small magnitude, and only the domain walls exhibit slightly higher
is roughly homogeneous over the whole lattice with small magnitude, and only the domain walls exhibit slightly higher  . Differently from this case, the lattice with the
. Differently from this case, the lattice with the  shows very high local
shows very high local  not only on the domain walls, as illustrated in fig. 4(c). The physics is simple. On the one hand, the sufficiently released dipole-dipole interaction and electromechanical energy by the voids introduction benefit substantially to the high mobility and deformation capability of the domains under electric field. On the other hand, the domain splitting allows the doubling of the domain walls, contributing to the electromechanical response.
not only on the domain walls, as illustrated in fig. 4(c). The physics is simple. On the one hand, the sufficiently released dipole-dipole interaction and electromechanical energy by the voids introduction benefit substantially to the high mobility and deformation capability of the domains under electric field. On the other hand, the domain splitting allows the doubling of the domain walls, contributing to the electromechanical response.
It should be mentioned that the present simulations are far from perfect. We only deal with the effects of the square void array on the  domain structure and electromechanical behaviors. Also, only the 2D thin film lattice with in-plane FE domains is considered here. One may consider various arrays of voids of different shapes and deal with more realistic domain structures in FE thin films, where in-plane domains and out-of-plane domains coexist. The simulations may be extended to 3D cases with much more complicated domain structures. Nevertheless, for these extended cases, the underlying physics would be similar and the core issue here is how to efficiently release and even modulate the concerned free energy terms by implanting various geometric structures, so that the favored FE and electromechanical performances can be enhanced. In this sense, the present work, in addition to the FE islands, disks, dots, or composite structures, may shed light on alternative approaches to engineer the domain structure of FE materials for specific purposes. In fact, a recent experiment revealed that introduction of low permittivity defects into
domain structure and electromechanical behaviors. Also, only the 2D thin film lattice with in-plane FE domains is considered here. One may consider various arrays of voids of different shapes and deal with more realistic domain structures in FE thin films, where in-plane domains and out-of-plane domains coexist. The simulations may be extended to 3D cases with much more complicated domain structures. Nevertheless, for these extended cases, the underlying physics would be similar and the core issue here is how to efficiently release and even modulate the concerned free energy terms by implanting various geometric structures, so that the favored FE and electromechanical performances can be enhanced. In this sense, the present work, in addition to the FE islands, disks, dots, or composite structures, may shed light on alternative approaches to engineer the domain structure of FE materials for specific purposes. In fact, a recent experiment revealed that introduction of low permittivity defects into  lamellae can dramatically modulate the domain switching dynamics [29]. An anisotropic electric field pattern near the air holes is believed to be responsible for the observed results. In the present work, the internal electric field also shows a spatial distribution due to the depolarization field near the film-void interface. This experiment together with our findings here allows us to believe that modification of the FE domain structure by introducing voids-like defects is effective.
lamellae can dramatically modulate the domain switching dynamics [29]. An anisotropic electric field pattern near the air holes is believed to be responsible for the observed results. In the present work, the internal electric field also shows a spatial distribution due to the depolarization field near the film-void interface. This experiment together with our findings here allows us to believe that modification of the FE domain structure by introducing voids-like defects is effective.
In summary, we have investigated the domain patterns and piezoelectricity of the tetragonal FE thin films with square grid structure. It is found that by properly choosing the size and array of the square voids, the stripe-like domains near the voids may spilt regularly. The competition between the dipole-dipole interaction and the electromechanical energy is responsible for the domain splitting. The calculations on the longitudinal piezoelectric coefficient predict a remarkable enhancement of the piezoelectric coefficient, caused by the sufficiently released dipole-dipole interaction and electromechanical energy due to the voids introduction and thus the doubling of domain walls.
Acknowledgments
This work was supported by the National Key Projects for Basic Researches of China (2015CB654602), the Natural Science Foundation of China (51431006, 51332006, 11374147), and the Priority Academic Program Development of Jiangsu Higher Education Institutions, China.









