Abstract
Conventional electron-phonon coupling induces either odd (triplet) or even (singlet) pairing states in a time reversal and inversion invariant Dirac semi-metal. It was shown that the energy of the singlet channel, always lower, prevails over the triplet. The role of both magnetic and non-magnetic spatial disorder was discovered. It is predicted that the magnetic part of scattering establishes a triplet ground state suppressing the singlet phase. On the other hand, the non-magnetic impurities slightly affecting the singlet phase may significantly suppress the triplet state.
Export citation and abstract BibTeX RIS
Introduction
Recently, solids with electronic states described by the Bloch wave functions, obeying the "pseudo-relativistic" Dirac equation (with Fermi velocity vF replacing the velocity of light) attracted widespread attention. One outstanding example is graphene, a two-dimensional (2D) hexagonal lattice made of carbon atoms. The 2D Dirac bi-spinor (spin in this case is actually a pseudo-spin/sublattice) incorporates excitations near its K and K' points in the Brillouin zone, so that the model is in fact of the two-band variety. Although a similar two-band electronic structure of bismuth was described long ago [1] (with spin replacing pseudo-spin), only recently several systems with strong spin-orbital interaction were demonstrated to exhibit their 3D Dirac quasiparticles [2–4]. Their discovery followed the recent exploration of the topological band theory [5].
A systematic proposal [6] to make a 3D Dirac semi-metal is to close the insulating gap by tuning a topological insulator towards the quantum phase transition (to trivial insulators) led to their discovery. The time-reversal invariant 3D Dirac point in materials like Na3Bi was theoretically investigated [7] and observed [2]. A well-known compound Cd3As2 is a symmetry-protected 3D Dirac semi-metal with a single pair of Dirac points in the bulk [4]. More recently, conductivity and magnetoabsorption of a zinc-blende crystal, HgCdTe, was measured [3] and are in agreement with the theoretical expectations in a Dirac semi-metal [8]. The discovery of the 3D Dirac materials makes it possible to investigate their physics including remarkable electronic properties. This is rich in new phenomena, and not seen in 2D Dirac semi-metals like graphene. Examples include the giant diamagnetism that diverges logarithmically when the chemical potential approaches the 3D Dirac point, slow dynamics, linear in frequency AC conductivity that has an imaginary part [8], quantum magnetoresistance showing linear field dependence in the bulk [9]. Most of the properties of these new materials were measured at relatively high temperatures. However, some of the topological insulators and suspected 3D Dirac semi-metals exhibit superconductivity at about the liquid-He temperature.
The well-known topological insulator Bi2Se3 doped with Cu, becomes a bulk superconducting at  [10]. Although in the bulk there appears the Dirac mass (gap) of order 0.1 eV at larger values of chemical potential the linear spectrum is dominant. When subjected to pressure [11], Tc increases to 7 K at 30 GPa. The quasilinear temperature dependence of the upper critical field Hc2 that exceeds the orbital and Pauli limits for the singlet pairing points to the triplet superconductivity. The band structure of the superconducting compounds is apparently not very different from its parent compound Bi2Se3. Electronic-structure calculations of the compound under pressure [11] reveal a single bulk three-dimensional Dirac cone like in Bi with large spin-orbit coupling. In addition, very recently there has been an indication that pnictide superconductors also possess 3D Dirac points [12].
[10]. Although in the bulk there appears the Dirac mass (gap) of order 0.1 eV at larger values of chemical potential the linear spectrum is dominant. When subjected to pressure [11], Tc increases to 7 K at 30 GPa. The quasilinear temperature dependence of the upper critical field Hc2 that exceeds the orbital and Pauli limits for the singlet pairing points to the triplet superconductivity. The band structure of the superconducting compounds is apparently not very different from its parent compound Bi2Se3. Electronic-structure calculations of the compound under pressure [11] reveal a single bulk three-dimensional Dirac cone like in Bi with large spin-orbit coupling. In addition, very recently there has been an indication that pnictide superconductors also possess 3D Dirac points [12].
Some experimental evidence point out to a "conventional" phononic pairing mechanism. The reported values of electron-electron interaction due to the phonons coupling constant λ are probably large with some reported values [13] well exceeding 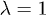 , which is stronger than in good low-Tc superconducting metals. The spin-independent part of the effective electron-electron interaction due to phonons was studied both theoretically and experimentally [14]. In addition, the layered, non-centrosymmetric heavy-element PbTaSe2 was found to be superconducting [15] following similar discoveries in YPtBi [16]. Its electronic properties like specific heat, electrical resistivity, and magnetic susceptibility indicate that PbTaSe2 is a moderately coupled, type-II BCS superconductor with large
, which is stronger than in good low-Tc superconducting metals. The spin-independent part of the effective electron-electron interaction due to phonons was studied both theoretically and experimentally [14]. In addition, the layered, non-centrosymmetric heavy-element PbTaSe2 was found to be superconducting [15] following similar discoveries in YPtBi [16]. Its electronic properties like specific heat, electrical resistivity, and magnetic susceptibility indicate that PbTaSe2 is a moderately coupled, type-II BCS superconductor with large 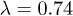 . It was shown theoretically to possess a very asymmetric 3D Dirac point created by strong spin-orbit coupling [17]. If the 3D is confirmed, it might indicate that the superconductivity is a conventional phonon-mediated coupling.
. It was shown theoretically to possess a very asymmetric 3D Dirac point created by strong spin-orbit coupling [17]. If the 3D is confirmed, it might indicate that the superconductivity is a conventional phonon-mediated coupling.
The case of a Dirac semi-metal is very special due to strong spin dependence of the itinerant electrons's effective Hamiltonian. It was pointed out [18,19] that in this case the triplet possibility can arise and although the triplet gap is smaller than that of the singlet, the difference sometimes is not large for spin-independent electron-electron interactions. Very recently the spin-dependent part of the phonon-induced electron-electron interaction was considered [20] and it was shown that the singlet gap is still larger than the triplet one. Another essential spin-dependent interaction is the exchange between itinerant electrons and magnetic impurities [21] like Cr/Fe in Bi2Se3. Obviously it favors the triplet. It is therefore of importance to clarify theoretically two questions: i) Does a conventional phononic superconductivity exists in these materials with just a minute density of states compared even with high-Tc cuprates that apparently utilize a very different pairing mechanism from the one that phonons offer? ii) Is it possible that phonons in 3D Dirac materials lead to triplet pairing that even becomes dominant under certain circumstances?
In the present letter we construct the theory of the superconducting transition in 3D Dirac semi-metal at arbitrary chemical potential including zero assuming the local (probably, but not necessarily, phonon-mediated) pairing. The possible pairing channels are classified in this rather unusual situation using symmetries of the system. In contrast to the 2D case, the odd-parity (triplet) pairing is not only possible, but with a small concentration of magnetic impurities the odd parity is the preferred channel taking over the more "conventional" even-parity one.
Symmetry classification of pairing channels
Electrons in 3D Dirac semi-metal are described by field operators 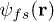 , where
, where 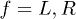 are the valley index for the left/right chirality bands with spin projections taking the values
are the valley index for the left/right chirality bands with spin projections taking the values  . These are combined into a four-component bi-spinor creation operator, whose index
. These are combined into a four-component bi-spinor creation operator, whose index  takes four values. The non-interacting massless Hamiltonian with chemical potential μ reads [7]
takes four values. The non-interacting massless Hamiltonian with chemical potential μ reads [7]
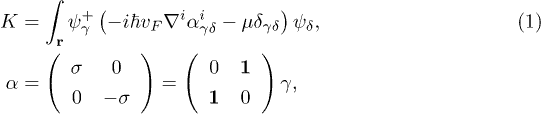
where 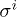 and 1 are the Pauli and the unit matrices, respectively. The mass (gap) term in the electron spectrum may be neglected, when the chemical potential significantly exceeding the gap value is considered. We also consider the time reversal, inversion and 3D rotational symmetry that in particular requires an isotropic Fermi velocity. Electrons interact electrostatically via the density-density potential. The effective electron-electron interaction due to both electron-phonon attraction and Coulomb repulsion (pseudo-potential) can be taken as local (assuming here and below that
and 1 are the Pauli and the unit matrices, respectively. The mass (gap) term in the electron spectrum may be neglected, when the chemical potential significantly exceeding the gap value is considered. We also consider the time reversal, inversion and 3D rotational symmetry that in particular requires an isotropic Fermi velocity. Electrons interact electrostatically via the density-density potential. The effective electron-electron interaction due to both electron-phonon attraction and Coulomb repulsion (pseudo-potential) can be taken as local (assuming here and below that 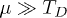 and the gap in the Dirac spectrum, where TD is the Debye temperature) [22]
and the gap in the Dirac spectrum, where TD is the Debye temperature) [22]

Unlike the free Hamiltonian K, eq. (1), this interaction Hamiltonian does not mix different spin components. Such a coupling implicitly restricts the spin-independent local interaction to be symmetric under the band permutation and the additional term is not generated. A more general case with an additional independent term was considered in ref. [18]. The strength of the phonon pairing depends on the cutoff TD.
Since we consider the local interactions as dominant, the superconducting order parameter will be local, 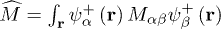 , where the constant matrix M should be antisymmetric. Due to the rotation symmetry they transform covariantly under infinitesimal rotations generated by the spin rotation generators Si, whose density is
, where the constant matrix M should be antisymmetric. Due to the rotation symmetry they transform covariantly under infinitesimal rotations generated by the spin rotation generators Si, whose density is
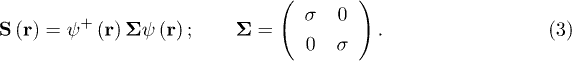
The representations of the rotation group therefore characterize various possible superconducting phases. Out of 16 possible matrices M, six are antisymmetric. One finds one vector of the rotation group triplet 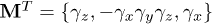 and three scalar multiplets:
and three scalar multiplets: 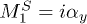 ;
; 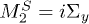 ;
; 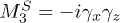 (see, for details, [22]). In the odd-parity superconductivity state the rotational O(3) symmetry is spontaneously broken, leading to weak ferromagnetism that has already been considered (on the level of the Ginzburg-Landau approach) for the heavy-fermion superconductor
(see, for details, [22]). In the odd-parity superconductivity state the rotational O(3) symmetry is spontaneously broken, leading to weak ferromagnetism that has already been considered (on the level of the Ginzburg-Landau approach) for the heavy-fermion superconductor  [23,24]. Which one of the condensates is realized depends on the energy determined by the interplay of the interactions and disorder. Let us first consider a clean homogeneous Dirac semi-metal.
[23,24]. Which one of the condensates is realized depends on the energy determined by the interplay of the interactions and disorder. Let us first consider a clean homogeneous Dirac semi-metal.
Singlet vs. triplet
The gap function for a channel M can be written [25] as
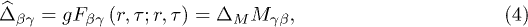
where 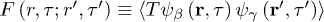 is the anomalous Matsubara Green's function (
is the anomalous Matsubara Green's function (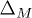 can be chosen real). The Fourier transform of F satisfies the matrix Gor'kov equation:
can be chosen real). The Fourier transform of F satisfies the matrix Gor'kov equation:
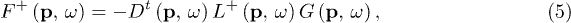
where 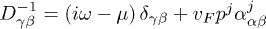 , while the Green's function G obeys the Dyson equation,
, while the Green's function G obeys the Dyson equation,

For the local phonon interaction, eq. (2), the operator
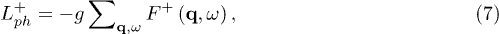
is independent of momenta and frequency and, in view of eq. (4), leads to an integrated form of the Gor'kov equation,
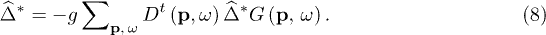
The equation is solved with UV cutoff TD characterizing the electron-phonon interaction along with the phonon-electron coupling 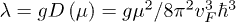 for the order parameter
for the order parameter 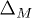 for all the channels. In fig. 1 the gap function for the singlet S1,
for all the channels. In fig. 1 the gap function for the singlet S1, 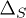 in red, and
in red, and 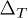 for the triplet in blue, for chemical potentials
for the triplet in blue, for chemical potentials 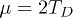 (left),
(left), 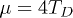 (center) and
(center) and 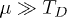 (right, the BCS limit). It turns out that S3 is unstable, while S1 and S2 are degenerate. The examination of the Green's function reveals, see [22], that the spectrum of excitations for the singlet is rotational invariant, while the one of the triplet has two nods. The value of the gap function itself does not define which channel is stable, so we have calculated the energy densities via momentum space Green's function for all the channels,
(right, the BCS limit). It turns out that S3 is unstable, while S1 and S2 are degenerate. The examination of the Green's function reveals, see [22], that the spectrum of excitations for the singlet is rotational invariant, while the one of the triplet has two nods. The value of the gap function itself does not define which channel is stable, so we have calculated the energy densities via momentum space Green's function for all the channels,

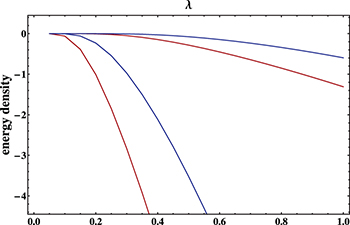
see, for details, [22]. Limiting cases of BCS when 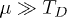 can be done analytically, while experimentally relevant (see below) chemical potentials
can be done analytically, while experimentally relevant (see below) chemical potentials 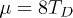 and 12TD are given for a wide range of couplings in fig. 2. The triplet (blue line) has always higher energy than the singlet. Magnetic impurities can strongly affect the relative energy of the triplet and especially the singlet condensates for which pair breaking occurs.
and 12TD are given for a wide range of couplings in fig. 2. The triplet (blue line) has always higher energy than the singlet. Magnetic impurities can strongly affect the relative energy of the triplet and especially the singlet condensates for which pair breaking occurs.
Fig. 1: (Colour on-line) Singlet (red) and triplet (blue) order parameters as a function of the phonon-mediated effective electron-electron coupling λ at three values of the chemical potential: 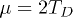 , 4TD and the BCS limit,
, 4TD and the BCS limit,  (from left to right).
(from left to right).
Download figure:
Standard imageFig. 2: (Colour on-line) Condensation energy in a clean singlet (red) and triplet (blue) superconductor as a function of the phonon-mediated effective electron-electron coupling λ at two values of the chemical potential:  (left), 12TD (right).
(left), 12TD (right).
Download figure:
Standard imageImpurities
If the Kondo temperature TK is small ( , here Tc is the critical superconducting temperature) then the electrons scatter from classical spins and physics in this regime can be described by the Gor'kov-Rusinov theory [26,27]. The Hamiltonian of the interaction with the impurities
, here Tc is the critical superconducting temperature) then the electrons scatter from classical spins and physics in this regime can be described by the Gor'kov-Rusinov theory [26,27]. The Hamiltonian of the interaction with the impurities
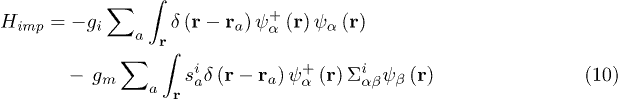
has exchange and direct parts (here sa represents the impurity spins located at 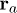 ). Below we only need the average over a random distribution of impurities values for exchange (magnetic disorder),
). Below we only need the average over a random distribution of impurities values for exchange (magnetic disorder),
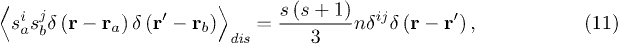
and direct scattering (non-magnetic disorder),
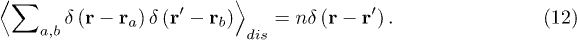
Here n is the density of the impurities and sℏ their spin.
Qualitatively, for the quadratic dispersion relation due to magnetic disorder, the singlet gains energy over the triplet and at certain disorder strength a phase transition from the singlet to the triplet might take place. At yet larger magnetic disorder strength the singlet channel becomes unstable and the triplet becomes the only stable channel. In a Dirac semi-metal the situation is different.
After averaging over the impurities of the kernel 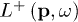 , the Gor'kov equation, eq. (5) acquires an additional term
, the Gor'kov equation, eq. (5) acquires an additional term 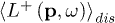 dependent on frequency ω for the singlet and triplet, respectively:
dependent on frequency ω for the singlet and triplet, respectively:
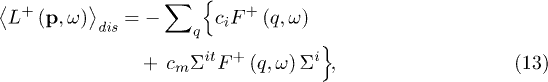
where
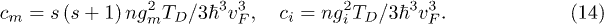
For the singlet and the triplet solutions one obtains
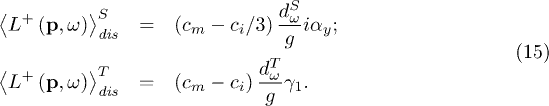
At a critical disorder strength 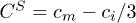 where the singlet channel is suppressed,
where the singlet channel is suppressed, 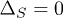 (so that
(so that 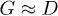 ), the Gor'kov equation integrated over the momenta takes the form
), the Gor'kov equation integrated over the momenta takes the form

where 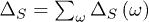 and
and
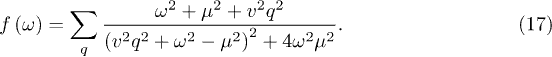
To solve the equations, one performs an integration over ω,

Similarly for the triplet, by using the critical strength 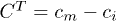 , one has
, one has

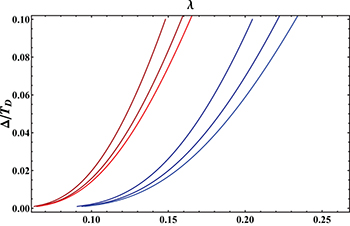
The phase diagram for the chemical potential 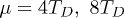 , 12TD in a wide range of λ and the critical concentration of the magnetic impurities cm at a fixed concentration of the non-magnetic impurities is presented in fig. 3. For each value of μ the singlet superconductivity disappears below the dashed line, while the triplet disappears below the solid line. It is clear that the triplet wins over at moderate magnetic impurity strength.
, 12TD in a wide range of λ and the critical concentration of the magnetic impurities cm at a fixed concentration of the non-magnetic impurities is presented in fig. 3. For each value of μ the singlet superconductivity disappears below the dashed line, while the triplet disappears below the solid line. It is clear that the triplet wins over at moderate magnetic impurity strength.
Fig. 3: (Colour on-line) Phase diagram of the magnetically doped 3D Dirac semi-metal in the  plane for different chemical potentials. λ is the phonon-mediated electron-electron coupling, while cm is the magnetic impurity strength from non-magnetic ones
plane for different chemical potentials. λ is the phonon-mediated electron-electron coupling, while cm is the magnetic impurity strength from non-magnetic ones 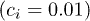 . The left group of curves where the order parameter
. The left group of curves where the order parameter 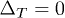 belongs to the triplet state, while the right group of curves where
belongs to the triplet state, while the right group of curves where 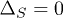 belongs to the singlet channel.
belongs to the singlet channel.
Download figure:
Standard imageSummary and discussion
To summarize, we presented a microscopic theory of superconductivity (at zero temperature) in massless Dirac semi-metals. In the framework of the "conventional" phonon-mediated local attraction model we classified (by simplifying the assumptions of the 3D rotation invariance, inversion and the time reversal) possible pairing channels. There are three even-parity (singlet) channels and one odd-parity (triplet) channel. In the clean limit the singlet pairing prevails for the arbitrary chemical potential and the electron-electron interaction strength. However, a modest concentration of magnetic impurities makes the triplet ground state as presented in fig. 3, which is the main result of our paper. In particular, the analysis of eq. (19) shows that non-magnetic impurities the affect the triplet state suppressing it at ci > cm. A larger magnetic impurity concentration suppresses the even parity state all together, while these impurities are not pair breaking for the odd-parity weakly ferromagnetic state.
To estimate the range of parameters for currently available materials where the odd-parity conventional (phonon-induced) superconductivity is expected, one should rely on measurements of the electron-phonon coupling. The effective dimensionless electron-electron coupling constant due to phonons λ for parent (non-superconducting) materials like Bi2Se3, Bi2Te3 reported in [28] vary widely in the range 0.1–3. Taking [13] for Bi2Se3 the Debye cutoff energy 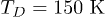 and
and 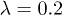 measured at
measured at 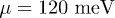 , the Fermi velocity of
, the Fermi velocity of 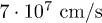 , one obtains the singlet 6 K superconductivity (see fig. 2), however disorder favours the triplet (see fig. 4). To destroy the singlet one, one needs to reach the impurity strength
, one obtains the singlet 6 K superconductivity (see fig. 2), however disorder favours the triplet (see fig. 4). To destroy the singlet one, one needs to reach the impurity strength 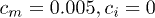 when that for the impurity spin s = 1 and the exchange integral of
when that for the impurity spin s = 1 and the exchange integral of  requires the impurity concentration
requires the impurity concentration 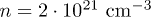 . If the Dirac mass is present in the spectrum (far from the surface) the calculations are valid only when the chemical potential is larger than this mass.
. If the Dirac mass is present in the spectrum (far from the surface) the calculations are valid only when the chemical potential is larger than this mass.
Fig. 4: (Colour on-line) Phase diagram of the magnetically and normally doped 3D Dirac semi-metal in the 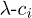 plane for different chemical potentials and for fixed cm. λ is the phonon-mediated electron-electron coupling, while ci is the magnetic impurity strength from non-magnetic ones
plane for different chemical potentials and for fixed cm. λ is the phonon-mediated electron-electron coupling, while ci is the magnetic impurity strength from non-magnetic ones 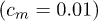 . Sold curves indicate where the order parameter
. Sold curves indicate where the order parameter 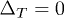 belongs to the triplet state while the dashed lines indicate where
belongs to the triplet state while the dashed lines indicate where 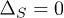 belongs to the singlet channel.
belongs to the singlet channel.
Download figure:
Standard imageThe physics of the triplet superconductors of this type is very rich and has already been investigated in connection with heavy-fermion superconductors. In particular, their magnetic vortices appear as either vector vortices or so-called skyrmions [23] —coreless topologically non-trivial textures. In particular, their magnetic properties like magnetization are very peculiar and even without magnetic field the system forms a "spontaneous flux state". The material therefore can be called "ferromagnetic superconductor". The superconducting state develops weak ferromagnetism and a system of alternating magnetic domains [24].
Acknowledgments
We are indebted to C. W. Luo, T. Maniv and M. Lewkowicz for valuable discussions. Work of BR and DL was supported by NSC of R.O.C. Grants No. 98-2112-M-009-014-MY3 and MOE ATU program. The work of DL is also supported by National Natural Science Foundation of China (No. 11274018).
Appendix
In this appendix we derive the Gor'kov equations (5) in the presence of impurities, both magnetic and non-magnetic, starting from the resummation of "bubble" diagrams of both phonon and impurities [26]. In the Nambu representation, normal and anomalous Green functions are combined into matrix

The generalized Dyson equations equivalent to self-consistent harmonic approximation read
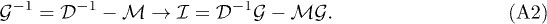
Here
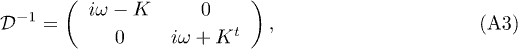
and the mass operator includes phonons and impurities matrix elements:
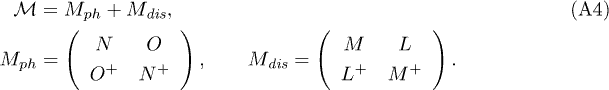
The matrix elements for the interaction with phonons are
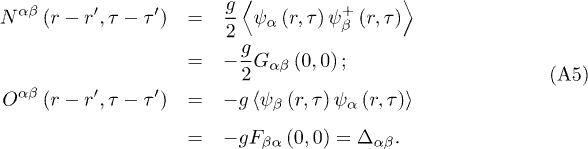
The disorder part after average over the disorder reads in momentum space
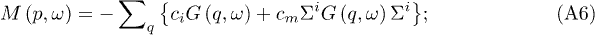

The influence of diagonal elements N and M is absorbed into a renormalized chemical potential.
In components eq. (A.2) takes the form
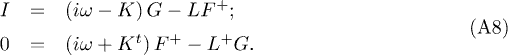
In the point where superconductivity disappears, F = 0, the first equation simplifies to

The second equation should be solved for small non-zero F,
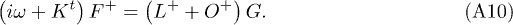
This results in eq. (5).