Abstract
A two-sublattice spin-fermion model of ferrimagnetic spinel, with spin-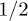 itinerant electrons at the sublattice A site and spin-s localized electrons at the sublattice B site is considered. The exchange between itinerant and localized electrons is antiferromagnetic. As a result, the external magnetic field, applied along the magnetization of the localized electrons, compensates the Zeeman splitting due to the spin-fermion exchange and magnon-fermion interaction induces spin antiparallel p-wave superconductivity which coexists with magnetism. We have obtained five characteristic values of the applied field (in units of energy) Hcr1 < H3 < H0 < H4 < Hcr2. At H0 the external magnetic field compensates the Zeeman splitting. When Hcr1 < H < Hcr2 the spin antiparallel p-wave superconductivity with T1u configuration coexists with magnetism. The superconductor-to-normal magnet transition at finite temperature is second order when H runs the interval
itinerant electrons at the sublattice A site and spin-s localized electrons at the sublattice B site is considered. The exchange between itinerant and localized electrons is antiferromagnetic. As a result, the external magnetic field, applied along the magnetization of the localized electrons, compensates the Zeeman splitting due to the spin-fermion exchange and magnon-fermion interaction induces spin antiparallel p-wave superconductivity which coexists with magnetism. We have obtained five characteristic values of the applied field (in units of energy) Hcr1 < H3 < H0 < H4 < Hcr2. At H0 the external magnetic field compensates the Zeeman splitting. When Hcr1 < H < Hcr2 the spin antiparallel p-wave superconductivity with T1u configuration coexists with magnetism. The superconductor-to-normal magnet transition at finite temperature is second order when H runs the interval  . It is an abrupt transition when Hcr1 < H < H3 or H4 < H < Hcr2. This is proved calculating the temperature dependence of the gap for three different values of the external magnetic field Hcr1 < H < H3, H4 < H < Hcr2 and
. It is an abrupt transition when Hcr1 < H < H3 or H4 < H < Hcr2. This is proved calculating the temperature dependence of the gap for three different values of the external magnetic field Hcr1 < H < H3, H4 < H < Hcr2 and 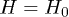 . In the first two cases the abrupt fall to zero of the gap at superconducting critical temperature shows that the superconductor-to-normal magnet transition is first order. The Hubbard term (Coulomb repulsion), in a weak-coupling regime, does not significantly affect the magnon-induced superconductivity. Relying on the above results one can formulate a recipe for preparing a superconductor from ferrimagnetic spinel: i) hydrostatic pressure above the critical value of insulator-metal transition; ii) external magnetic field along the sublattice magnetization with higher amplitude.
. In the first two cases the abrupt fall to zero of the gap at superconducting critical temperature shows that the superconductor-to-normal magnet transition is first order. The Hubbard term (Coulomb repulsion), in a weak-coupling regime, does not significantly affect the magnon-induced superconductivity. Relying on the above results one can formulate a recipe for preparing a superconductor from ferrimagnetic spinel: i) hydrostatic pressure above the critical value of insulator-metal transition; ii) external magnetic field along the sublattice magnetization with higher amplitude.
Export citation and abstract BibTeX RIS
Introduction
Electron-phonon mechanism of superconductivity [1–4] has been developed to explain the pairing in a large variety of materials, from Hg and Al to recently discovered MgB2 [5]. The discovery of superconductivity in LaBaCuO [6] and in other cuprates, as well as the discovery of superconductivity in Fe-based pnictides [7] established another direction of research in this field. The boson-fermion models still remained respected but bosons are not lattice vibrations.
Alternatively, the possibility of an electronic pairing mechanism in systems with rotational invariance was put forward in a seminal paper by Kohn and Luttinger [8–10]. Although the bare interaction among electrons is repulsive, there is an effective attractive interaction that arises at higher order of perturbation theory. The Kohn-Luttinger instability of a three-dimensional rotationally invariant system results in the formation of an unconventional superconducting ground state due to the peak in the particle-hole susceptibility near zero wave vector. The works [11–15] have made significant progress in our understanding of superconductivity from repulsive interaction.
There are many experiments addressing external magnetic-field-induced, enhanced or re-entered superconductivity. Experimentally, an anomalous enhancement of  was first reported by Fischer et al. [16]. An increase of about
was first reported by Fischer et al. [16]. An increase of about  of the upper critical field is observed in Sn1.2(1-x)EuxMo6.35S8 and Pb1-xEux Mo6.35S8 with respect to the compounds without Eu. The overall feature of the field-induced superconducting phase is well understood by a theory based on the Jaccarino-Peter (JP) compensation mechanism [17].
of the upper critical field is observed in Sn1.2(1-x)EuxMo6.35S8 and Pb1-xEux Mo6.35S8 with respect to the compounds without Eu. The overall feature of the field-induced superconducting phase is well understood by a theory based on the Jaccarino-Peter (JP) compensation mechanism [17].
In a rare-earth ferromagnetic metal the conduction electrons are in an effective field due to the exchange interaction with the rare-earth spins. It is in general so large as to inhibit the occurrence of superconductivity. For some systems the exchange interaction has a negative sign. This allows for the conduction electron polarization to be canceled by an external magnetic field so that if, in addition, these metals possess phonon-induced attractive electron-electron interaction, superconductivity occurs in the compensation region. If the effective field is not large the coexistence of superconductivity and magnetic order is possible and the external magnetic field enhances the superconductivity. The effect can also be observed in a paramagnet since the strong external field will in any case polarize the localized magnetic moments at low temperature, and thus produce the necessary ferromagnetic alignment [18]. Therefore, superconductivity can occur in two domains: one at the low field, where the pair-breaking field is still small, and one at the high field in the compensation region. The field re-entrance of superconductivity was first reported in [19,20].
The JP compensation mechanism was originally proposed to explain the superconductivity in some pseudoternary materials. Recently, the JP effect has been proven to be responsible for the magnetic-field-induced superconductivity in the organic superconductor λ-(BETS)2FeCl4 [21,22].
The superconductivity in the Jaccarino-Peter theory is induced by phonon fluctuations and spin fluctuations (magnons) weaken the spin singlet Cooper pairing. In the present paper we consider magnon-induced superconductivity based on the compensation mechanism [17]. We study the conditions for the coexistence of superconductivity and magnetism in a spin-fermion system which is a prototype model of itinerant ferrimagnetic spinel. A two-sublattice system is defined on a body-centered-cubic lattice, with spin-1/2 itinerant electrons at the sublattice A site and spin-s localized electrons at the sublattice B site. The subtle point is the exchange between itinerant and localized electrons which is antiferromagnetic and applying an external magnetic field along the magnetization of the localized electrons one can compensate the Zeeman splitting due to the spin-fermion exchange. Then, magnon-fermion interaction induces spin antiparallel p-wave superconductivity, with T1u configuration, which coexists with magnetism. We have studied the superconducting gap as a function of applied magnetic field and temperature. The Coulomb repulsion, in a weak-coupling regime, does not affect significantly the magnon-induced superconductivity.
Relying on the above results one can formulate a recipe for preparing a superconductor from ferrimagnetic spinel: i) hydrostatic pressure above the critical value of insulator-metal transition; ii) external magnetic field along the sublattice magnetization with higher amplitude. In favor of this recipe one can mention that metallization in magnetite Fe3O4 is found under a pressure above 8GPa [23–25]. While the model under consideration does not match well the Fe3O4 system we expect to find superconductivity applying external magnetic field along sublattice B magnetization, when the hydrostatic pressure is above the critical one.
On the other hand, there are spinel compounds well known as superconductors at ambient pressure: CuRh2Se4,CuRh2S4 [26–31]. The results of the present paper inspire that applying external magnetic field one can expect an enhancement of the superconducting transition temperature Tsc. This is a quite specific phenomenon for the spinel superconductivity and it deserves to be experimentally verified.
Spin-fermion model of ferrimagnetic spinel
The Hamiltonian of the spin-fermion model of ferrimagnetic spinel defined on a body-centered-cubic lattice is
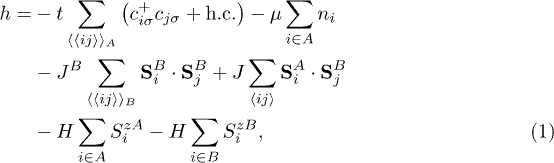
where 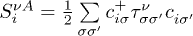 , with the Pauli matrices
, with the Pauli matrices 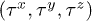 , is the spin of the itinerant electrons at the sublattice A site,
, is the spin of the itinerant electrons at the sublattice A site, 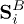 is the spin of the localized electrons at the sublattice B site, μ is the chemical potential, and
is the spin of the localized electrons at the sublattice B site, μ is the chemical potential, and 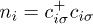 . The sums are over all sites of a body-centered-cubic lattice,
. The sums are over all sites of a body-centered-cubic lattice, 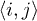 denotes the sum over the nearest neighbors, while
denotes the sum over the nearest neighbors, while  and
and  are sums over all sites of sublattice A and B, respectively. The Heisenberg term
are sums over all sites of sublattice A and B, respectively. The Heisenberg term 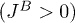 describes ferromagnetic Heisenberg exchange between localized electrons and J > 0 is the antiferromagnetic exchange constant between localized and itinerant electrons. H > 0 is the Zeeman splitting energy due to the external magnetic field (magnetic field in units of energy).
describes ferromagnetic Heisenberg exchange between localized electrons and J > 0 is the antiferromagnetic exchange constant between localized and itinerant electrons. H > 0 is the Zeeman splitting energy due to the external magnetic field (magnetic field in units of energy).
To proceed we use the Holstein-Primakoff representation of the spin operators of localized electrons 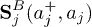 , where
, where 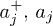 are Bose fields. In terms of these fields and keeping only the quadratic terms, the Hamiltonian equation (1) is a sum of three terms:
are Bose fields. In terms of these fields and keeping only the quadratic terms, the Hamiltonian equation (1) is a sum of three terms:

where
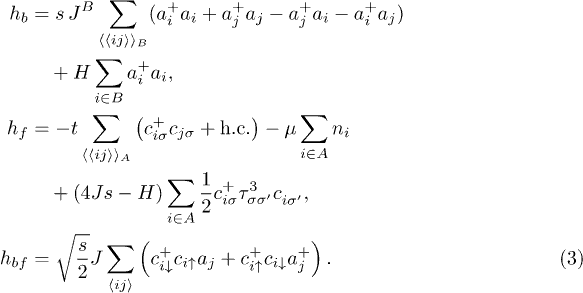
In momentum space representation, the Hamiltonian reads
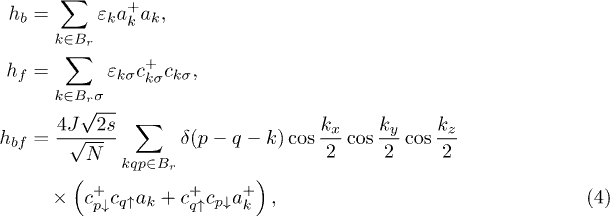
with Bose 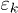 and Fermi
and Fermi 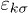 dispersions
dispersions
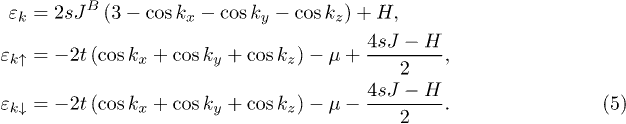
The two equivalent sublattices A and B of the body-centered-cubic lattice are simple cubic lattices. Therefor the wave vectors p, q, k run over the first Brillouin zone of a cubic lattice Br.
Magnon-induced superconductivity
Let us average in the subspace of Bosons 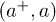 (to integrate the Bosons in the path integral approach). In static approximation one obtains an effective fermion theory with Hamiltonian
(to integrate the Bosons in the path integral approach). In static approximation one obtains an effective fermion theory with Hamiltonian 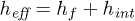 , where hf is the free fermion Hamiltonian equation (4) and the magnon-induced four-fermion interaction is
, where hf is the free fermion Hamiltonian equation (4) and the magnon-induced four-fermion interaction is
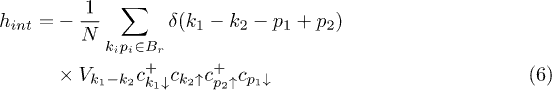
with potential
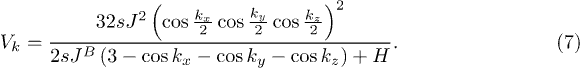
Following standard procedure one obtains the effective Hamiltonian in the Hartree-Fock approximation
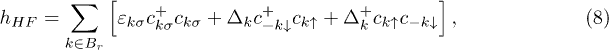
with gap function

The Hamiltonian can be written in a diagonal form by means of Bogoliubov excitations 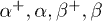 , which have the following dispersions:
, which have the following dispersions:
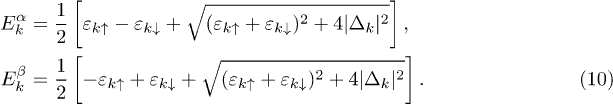
In terms of the new excitations the gap equation reads
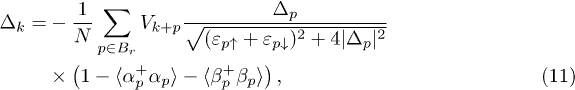
where 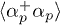 and
and  are Fermi functions for Bogoliubov fermions.
are Fermi functions for Bogoliubov fermions.
Straightforward calculations show that eq. (11) has not spin-singlet 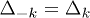 solutions. Having in mind that sublattices are simple cubic lattices and following the classifications for spin-triplet gap functions
solutions. Having in mind that sublattices are simple cubic lattices and following the classifications for spin-triplet gap functions 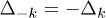 , we obtained that A1u state
, we obtained that A1u state 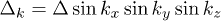 is not a solution of eq. (11) too. The gap function with T1u configuration
is not a solution of eq. (11) too. The gap function with T1u configuration
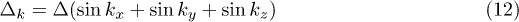
is a solution of the gap equation for some values of the external magnetic field and temperature.
It follows from eq. (5), that the external magnetic field (in units of energy) compensates the Zeeman splitting, due to the spin-fermion exchange, at  . We calculate the gap parameter Δ, from eq. (11), as a function of
. We calculate the gap parameter Δ, from eq. (11), as a function of  , setting the chemical potential μ equal to zero. The last means that in normal phase the density of sublattice A itinerant electrons is n = 1. We have obtained four characteristic values of the applied field Hcr1 < H3 < H0 < H4 < Hcr2. When Hcr1 < H < Hcr2 the spin antiparallel p-wave superconductivity with T1u configuration coexists with magnetism. The thermal superconductor-to-normal magnet transition is second order when H runs the interval
, setting the chemical potential μ equal to zero. The last means that in normal phase the density of sublattice A itinerant electrons is n = 1. We have obtained four characteristic values of the applied field Hcr1 < H3 < H0 < H4 < Hcr2. When Hcr1 < H < Hcr2 the spin antiparallel p-wave superconductivity with T1u configuration coexists with magnetism. The thermal superconductor-to-normal magnet transition is second order when H runs the interval 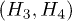 . It is an abrupt transition when Hcr1 < H < H3 or H4 < H < Hcr2. The dimensionless gap
. It is an abrupt transition when Hcr1 < H < H3 or H4 < H < Hcr2. The dimensionless gap 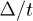 as a function of
as a function of 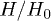 at zero temperature is depicted in fig. 1 for parameters
at zero temperature is depicted in fig. 1 for parameters 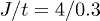 and
and 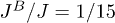 . The critical values of the external magnetic fields are
. The critical values of the external magnetic fields are  and
and 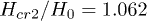 . The red vertical lines in fig. 1 correspond to the
. The red vertical lines in fig. 1 correspond to the 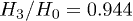 and
and 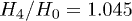 .
.
Fig. 1: (Color online) Dimensionless gap  as a function of
as a function of 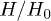 . The critical values are
. The critical values are 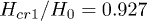 and
and 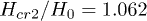 . The red lines correspond to
. The red lines correspond to 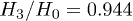 and
and 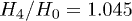 . When
. When 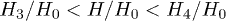 the thermal superconductor-to-normal magnet transition is second order. In other cases it is abrupt.
the thermal superconductor-to-normal magnet transition is second order. In other cases it is abrupt.
Download figure:
Standard imageTo demonstrate the nature of the thermal superconductor-normal magnet transition, we have calculated the gap 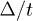 as a function of the temperature T/t for three different values of the external magnetic field:
as a function of the temperature T/t for three different values of the external magnetic field: 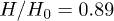 ,
, 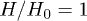 and
and 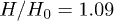 . The result is shown in fig. 2. The black line represents
. The result is shown in fig. 2. The black line represents 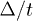 as a function of T/t for
as a function of T/t for 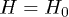 . The second-order phase transition demonstrates itself through the smooth decrease of the gap up to zero at critical temperature
. The second-order phase transition demonstrates itself through the smooth decrease of the gap up to zero at critical temperature 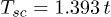 . The other two lines, blue
. The other two lines, blue 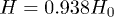 and red
and red  , demonstrate abrupt fall of the gap at superconducting critical temperatures
, demonstrate abrupt fall of the gap at superconducting critical temperatures 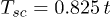 and
and 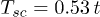 , respectively.
, respectively.
Fig. 2: (Color online) Dimensionless gap  as a function of dimensionless temperature T/t. The black line represents the function for
as a function of dimensionless temperature T/t. The black line represents the function for 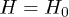 , the blue line stands for
, the blue line stands for 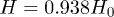 and the red line stands for
and the red line stands for 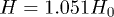 .
.
Download figure:
Standard imageTo account for the Coulomb repulsion one has to add the Hubbard term to the Hamiltonian equation (1):
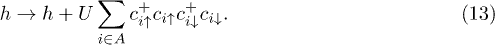
When the coupling U/t is strong enough the model describes a system of localized electrons on sublattice A sites. Under the pressure, the charge screening increases (the Coulomb repulsion U decreases) and overlap of the wave functions of electrons increases (the hopping parameter t increases). As a result the coupling constant U/t decreases and we can treat the Hubbard term in a weak-coupling regime.
The contribution of the first-order term in U/t expansion to the magnon-induced superconductivity changes the potential equation (7)  . It is known [15] that this term does not contribute to any unconventional channel of superconductivity. To assess the suppression of the superconductivity due to the first term we calculate the superconducting critical temperature as a function of U/t for
. It is known [15] that this term does not contribute to any unconventional channel of superconductivity. To assess the suppression of the superconductivity due to the first term we calculate the superconducting critical temperature as a function of U/t for  ,
,  and
and 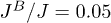 . When the Zeeman splitting is compensated
. When the Zeeman splitting is compensated 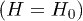 the thermal superconductor-normal magnet transition is a second order and we can use the linearized gap equation to determine the critical temperature Tsc as a function of the Coulomb repulsion U
the thermal superconductor-normal magnet transition is a second order and we can use the linearized gap equation to determine the critical temperature Tsc as a function of the Coulomb repulsion U
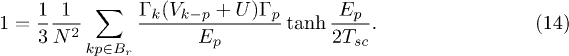
In eq. (14) 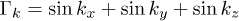 and
and 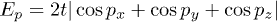 .
.
The result shows that the contribution of the first-order term in U/t expansion to the magnon-induced superconductivity is unessential. For example for 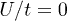 the critical temperature is
the critical temperature is 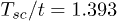 , while for
, while for 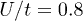 it is
it is 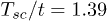 .
.
The higher-order terms in a weak-coupling expansion contribute to the superconductivity through the Kohn-Luttinger mechanism. The results show [14] that the effect on the p-wave superconductivity with T1u configuration is weak. This permits to conclude that the Coulomb repulsion, in a weak-coupling regime, does not impact significantly the magnon-induced superconductivity and we can drop it.
Finally, we consider the effect of the chemical manipulation. To this end we study the critical temperature Tsc as a function of the density of states of itinerant electrons in normal phase for the same parameters of the system as above. The equation for the critical temperature Tsc is eq. (14) with U = 0 and ![$E_p=\sqrt{[2t(\cos p_x+\cos p_y+\cos p_z )+\mu]^2}$](https://content.cld.iop.org/journals/0295-5075/110/2/27004/revision1/epl17039ieqn73.gif) , where μ is the chemical potential. Table 1 shows that decreasing the density of itinerant electrons, the superconducting critical temperature
, where μ is the chemical potential. Table 1 shows that decreasing the density of itinerant electrons, the superconducting critical temperature 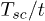 slowly decreases. This is true if the electrons are delocalized. If the sublattice A electrons are localized the deviation from half-filling is a way to delocalize them and we expect an opposite tendency.
slowly decreases. This is true if the electrons are delocalized. If the sublattice A electrons are localized the deviation from half-filling is a way to delocalize them and we expect an opposite tendency.
Table 1:. The table shows that decreasing the density of itinerant electrons, the superconducting critical temperature 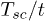 decreases very slowly.
decreases very slowly.
| n | 1 | 0.9 | 0.8 | 0.7 | 0.6 |
|---|---|---|---|---|---|
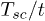 |
1.393 | 1.3873 | 1.3761 | 1.3534 | 1.3169 |
Conclusion
In summary, we have proposed a method of preparation of superconducting ferrimagnetic spinel. We have studied a two-sublattice spin-fermion model of ferrimagnetic spinel, with spin-1/2 itinerant electrons at the sublattice A site and spin-s localized electrons at the sublattice B site in an external magnetic field, applied along the magnetization of the localized electrons. Magnon-induced superconductivity is predicted when the Coulomb repulsion is small (the system is under hydrostatic pressure) and the external magnetic field compensates the Zeeman splitting due to the spin-fermion exchange. The main point is that the exchange between itinerant and localized electrons is antiferromagnetic 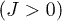 . It is evident from eq. (5) that the sign of J is crucial the external magnetic field H, applied along the magnetization of the localized electrons, to compensate the Zeeman splitting. As a result magnon-fermion interaction induces spin antiparallel p-wave superconductivity, which coexists with magnetism.
. It is evident from eq. (5) that the sign of J is crucial the external magnetic field H, applied along the magnetization of the localized electrons, to compensate the Zeeman splitting. As a result magnon-fermion interaction induces spin antiparallel p-wave superconductivity, which coexists with magnetism.
There are many experimental [32–34] and theoretical [35–38] papers on coexisting of ferromagnetism and superconductivity. Although the singlet pairing has been proposed [37,38] the most popular theory of ferromagnetic superconductivity is based on the paramagnon (longitudinal ferromagnetic fluctuations) exchange mechanism [35,36]. The order parameters are spin parallel components of spin triplets and the ferromagnetic superconductivity appears on the border of itinerant magnetism [32]. This is in stark contrast to the ferrimagnetic superconductor, discussed in the present paper, which is the result of magnon-fermion interaction. The order parameter is spin antiparallel component of a spin triplet and the saturation magnetization (in units of 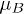 ) is close to 2s in the superconducting phase.
) is close to 2s in the superconducting phase.
The spin-fermion exchange J induces a magnetic moment and the transversal fluctuations flip the spin of the sublattice B electrons. This destroys s-type Cooper pairs 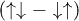 but supports the p-type
but supports the p-type 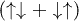 ones, which have zero spin projection. The effect is unessential near the zero Zeeman splitting.
ones, which have zero spin projection. The effect is unessential near the zero Zeeman splitting.
If the Zeeman splitting is very small, compared to the gap, the s-type superconducting state is stable. If it is much larger than the gap, the superconducting state will turn into a normal state. It was argued by Fulde and Ferrell [39], Larkin and Ovchinnikov [40] that an inhomogeneous superconducting state, with pairing order parameter oscillating in space, may be the ground state when the Zeeman splitting is comparable to the energy gap. The Cooper pairs carry a finite momentum in the Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) state. One expects that, in the present model, below the critical field Hcr1 and above Hcr2, inhomogeneous superconducting state is possible increasing the superconducting dome, fig. 1.
There are two methods of preparation of spinel ferrimagnetics. If, during the preparation, an external magnetic field as high as 300 Oë is applied upon cooling, the material is named field-cooled (FC). If the applied field is about 1Oë the material is zero-field–cooled (ZFC). The magnetization-temperature [41] and magnetic susceptibility [42,43] curves for these materials display a pronounced bifurcation below Néel temperature TN. The ZFC curve exhibits a maximum and then a monotonic decrease upon cooling from TN, while the FC curve increases steeply, which shows a dip near the temperature at which the ZFC curve has a maximum and finally increases monotonically [43]. The magnetization-temperature curve is close to the reference curve obtained from contribution of localized spins on the one of the sublattices. Hence, in FC materials the electrons on the other sublattice have dispersion with approximately compensated Zeeman splitting. This permits to think that at high hydrostatic pressure these materials will have a superconducting state.
The Zeeman splitting energy H0 can be obtained from the external magnetic field used for the preparation of FC material. For MnV2O4 the field is as high as 300 Oë [43].
The model we have considered is a prototype model of itinerant ferrimagnetic spinel. It is a prototype model because the sublattice A sites are occupied, usually, by more than one electron. But this is not a toy model, because it captures all physical relevant properties of the spinel system and the existence of more than one electron on sublattice A sites will not change the conclusion that the magnon-induced superconductivity exists upon some conditions.







