Abstract
Quantum algorithms often assume independent spin qubits to produce trivial  ,
,  mappings. This can be unrealistic in many solid-state implementations with sizeable magnetic interactions. Here we show that the lower part of the spectrum of a molecule containing three exchange-coupled metal ions with
mappings. This can be unrealistic in many solid-state implementations with sizeable magnetic interactions. Here we show that the lower part of the spectrum of a molecule containing three exchange-coupled metal ions with  and
and  is equivalent to nine electron-nuclear qubits. We derive the relation between spin states and qubit states in reasonable parameter ranges for the rare earth Tb3+ and for the transition metal Cu2+, and study the possibility to implement Shor's Quantum Error Correction code on such a molecule. We also discuss recently developed molecular systems that could be adequate from an experimental point of view.
is equivalent to nine electron-nuclear qubits. We derive the relation between spin states and qubit states in reasonable parameter ranges for the rare earth Tb3+ and for the transition metal Cu2+, and study the possibility to implement Shor's Quantum Error Correction code on such a molecule. We also discuss recently developed molecular systems that could be adequate from an experimental point of view.
Export citation and abstract BibTeX RIS
Introduction
A key problem of quantum computing is derived from the no-cloning theorem [1,2] which states that an unknown quantum state cannot be copied. This means that the classical error correction scheme consisting on preparing several copies of a bit and taking periodic "majority votes" to discard the occasional noisy bit is not usable. Instead, a known relation is established among a group of redundant qubits which actually only contain one qubit of useful information. Then, after an error, this relation can be restored without perturbing the actual value of the qubit. This recovery of the quantum information without performing a projective measurement must be an essential feature of any scalable quantum information processing design.
For the implementation of scalable Quantum Information Processing Devices, molecular electron spin qubits are very promising. Indeed, g-tensor engineering has been achieved to prepare an electron spin-qubit version of a Lloyd (ABC)n model [3,4]. Recently, the coherence time of molecular rare-earth complexes has been extended by means of chemical design and/or optimal experimental conditions, allowing a high number of coherent Rabi oscillations [5,6]. Scalability would be achieved by combining these solid-state qubits with qubits of other nature, e.g., photons or micro-SQUIDs. This possibility is getting closer with the advances in heterogeneous quantum information processing [7]. While this is still a long-term goal, it is worth mentioning that superconducting coplanar waveguide resonators have been recently reported [8], which can be strongly coupled to single magnetic crystals, or even to individual molecular spins [9]. Transferring the quantum information from the solid-state spin qubit to the "flying" optical qubit is a crucial step towards the scalability of proposals such as the present one. One can foresee that, while the quantum operations take place in a different part of the device, a qubit could be coherently transferred to a magnetic molecule in the form of a photon, the molecule could be subjected to a Quantum Error Correction protocol during a "storage time", and then the protected qubit could be coherently transferred back to a photon to continue the quantum information processing.
It is known that molecules containing more than one spin can be used for Quantum Error Correction (QEC), i.e. complex molecules can be designed to function as a single encoded qubit. Except for a phase factor which does not affect any observable, selective 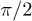 and π pulses are available both for the Hadamard and for the CNOT gate in pulsed magnetic resonance spectroscopy. Indeed, this line of research has been developed for the last 15 years [10–15].
and π pulses are available both for the Hadamard and for the CNOT gate in pulsed magnetic resonance spectroscopy. Indeed, this line of research has been developed for the last 15 years [10–15].
So far, these efforts have been largely limited to nuclear spins, while magnetic metal complexes have —except in a few cases— [16] been used in the context of Quantum Computing just as proof-of-principle toy models [17,18] or to obtain enhanced properties [19]. In the near future, the avenue of electronic spins needs to be explored, since the coupling of electron spins with qubits of different nature holds great promise. As recent notable examples, superconducting qubits have been interfaced with telecom photons via rare-earth complexes [20] and a rare earth has been locally implanted in a superconducting micro-resonator without degrading its internal quality factor [21]. In the mid-term, there is no fundamental reason that impedes this avenue leading to molecular (i.e., tuneable) analogues of the NV centers in diamond, where QEC has also been recently demonstrated [22]. In this work, we suggest that some polynuclear metal complexes can also be used to construct non-trivial building blocks capable of Quantum Error Correction.
The most conceptually simple —while general— implementation of this strategy is the Shor code [23], which belongs to the Bacon-Shor error correcting code class. This class of codes tend to have simpler correction circuits, which increases the likelihood of finding an experimental system where they can be carried out. Moreover, Bacon-Shor codes for a given number and kind of errors can in general be adapted roughly preserving their structure. This opens the possibility of in situ adapting the error correction to the nature of the noise in the physical system.
In this work, we will show that the Shor code could be implemented by using electron-nuclear Bell states of three magnetic ions. A well-isolated electron doublet is easily achievable in lanthanoids which would contribute one qubit per ion [24,25]; to reach the required nine qubits we would need two additional qubits per nuclear spin. Therefore, 159Tb3+, with 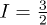 and a 100% natural isotopic purity, would be the perfect candidate for this goal, assuming the lowest electronic doublet has a sufficiently large gap Ω to the next excited level. Note that the four quantum states of the spin
and a 100% natural isotopic purity, would be the perfect candidate for this goal, assuming the lowest electronic doublet has a sufficiently large gap Ω to the next excited level. Note that the four quantum states of the spin 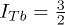 are exactly equivalent, from the point of view of their quantum information content, to the four quantum states of two uncoupled spins
are exactly equivalent, from the point of view of their quantum information content, to the four quantum states of two uncoupled spins 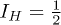 , and thus can be used as two qubits. Alternatively, one could use a trimer of 63Cu2+ (or 65Cu2+), also with
, and thus can be used as two qubits. Alternatively, one could use a trimer of 63Cu2+ (or 65Cu2+), also with 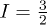 and where it is also trivial to achieve a spin doublet (other transition metal candidates exist but are less convenient). In any case, the three nuclear quadruplets combined with the three electronic doublets would provide a
and where it is also trivial to achieve a spin doublet (other transition metal candidates exist but are less convenient). In any case, the three nuclear quadruplets combined with the three electronic doublets would provide a 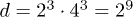 Hilbert space, i.e. the basis of 9 qubits.
Hilbert space, i.e. the basis of 9 qubits.
Definition of the system
Let us begin by considering the low-energy spectrum of three coupled 159Tb3+ ions, i.e. the full 43 states resulting from the three 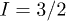 nuclear spins and the lowest 23 substates of three
nuclear spins and the lowest 23 substates of three 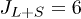 electronic spins (fig. 1). Note that effective spins
electronic spins (fig. 1). Note that effective spins  which are commonly used to reproduce spin qubits have two shortcomings in this situation: 1) they cannot have tunneling splitting, an important feature of non-Kramers rare earth systems and 2) the magnetic coupling of two
which are commonly used to reproduce spin qubits have two shortcomings in this situation: 1) they cannot have tunneling splitting, an important feature of non-Kramers rare earth systems and 2) the magnetic coupling of two  produces a different energy level scheme: a triplet plus a singlet instead of the expected doublet-plus-two-degenerate-singlets. Thus, we approximate the low-energy doublet of these
produces a different energy level scheme: a triplet plus a singlet instead of the expected doublet-plus-two-degenerate-singlets. Thus, we approximate the low-energy doublet of these  electronic states by S = 1 spins with effectively infinite axial zero-field splittings —and therefore also infinite gap Ω to the first excited level— to produce the correct energy level scheme and tunneling splitting. Indeed, up to linear scaling factors in D, E and g, the low-energy level scheme of three exchange-coupled S = 1 spins is almost identical to that of three exchange-coupled S = 6 spins (details in the Supplementary Material given in [26]).
electronic states by S = 1 spins with effectively infinite axial zero-field splittings —and therefore also infinite gap Ω to the first excited level— to produce the correct energy level scheme and tunneling splitting. Indeed, up to linear scaling factors in D, E and g, the low-energy level scheme of three exchange-coupled S = 1 spins is almost identical to that of three exchange-coupled S = 6 spins (details in the Supplementary Material given in [26]).
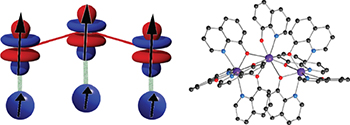
Fig. 1: (Color online) Left: interaction scheme between three electronic spins (doublet ground state) and three nuclear spins quadruplet 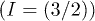 , resulting in
, resulting in 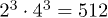 states or 9 qubits. Right: an experimental example of Tb3+ trimer, Tb3(OQ)9.
states or 9 qubits. Right: an experimental example of Tb3+ trimer, Tb3(OQ)9.
Download figure:
Standard imageWe apply the following Hamiltonian:

where Jex is the magnetic exchange, 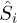 are effective electron S = 1 spins,
are effective electron S = 1 spins, 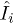 are nuclear
are nuclear 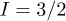 spins, D is the linear zero-field splitting, E is the rhombic zero-field splitting, A is the hyperfine coupling, P is the nuclear quadrupole term, ge is the effective electronic Landé factor, gI is the effective nuclear Landé factor,
spins, D is the linear zero-field splitting, E is the rhombic zero-field splitting, A is the hyperfine coupling, P is the nuclear quadrupole term, ge is the effective electronic Landé factor, gI is the effective nuclear Landé factor,  and
and 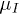 are the Bohr magneton and the nuclear magneton, and Hz is the external field.
are the Bohr magneton and the nuclear magneton, and Hz is the external field.
For Tb3+ we assume common values for hyperfine coupling 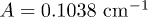 , nuclear quadrupole term
, nuclear quadrupole term 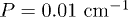 and effective nuclear Landé factor
and effective nuclear Landé factor 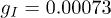 . We are employing an effective S = 1 instead of the typical
. We are employing an effective S = 1 instead of the typical 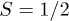 , resulting in an effective Landé factor
, resulting in an effective Landé factor  which is equivalent to a typical effective Landé factor
which is equivalent to a typical effective Landé factor  for terbium. In our calculations, we explore a certain range of magnetic exchange Jex, rhombic zero-field splitting E (accounting for tunneling splitting Δ) and external field Hz, as these parameters can be varied with a certain ease, either by chemical or experimental design. In particular, we explore a three-dimensional parameter space defined by
for terbium. In our calculations, we explore a certain range of magnetic exchange Jex, rhombic zero-field splitting E (accounting for tunneling splitting Δ) and external field Hz, as these parameters can be varied with a certain ease, either by chemical or experimental design. In particular, we explore a three-dimensional parameter space defined by 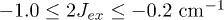 ,
, 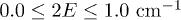 ,
, 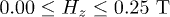 . Note that here Jex is acting on an effective S = 1. The range of both magnetic exchange and tunneling splitting
. Note that here Jex is acting on an effective S = 1. The range of both magnetic exchange and tunneling splitting 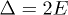 corresponds to typical values among lanthanoid complexes. We simplified the exploration of the three-dimensional parameter space by choosing the
corresponds to typical values among lanthanoid complexes. We simplified the exploration of the three-dimensional parameter space by choosing the 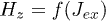 surface such that the splitting corresponding to a typical Zeeman electronic transition corresponds to a standard W-band apparatus 95 GHz (other transitions would of course require a non-standard setup with additional frequencies, see below). This corresponds to
surface such that the splitting corresponding to a typical Zeeman electronic transition corresponds to a standard W-band apparatus 95 GHz (other transitions would of course require a non-standard setup with additional frequencies, see below). This corresponds to 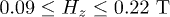 . We diagonalize the Hamiltonian with the MAGPACK software package [27,28].
. We diagonalize the Hamiltonian with the MAGPACK software package [27,28].
In a second independent exploration, we consider three exchange-coupled 63Cu2+ (S = 1/2). This gives us the opportunity to explore a different parameter space, namely 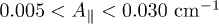 ,
, 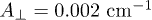 ,
, 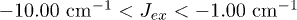 ,
, 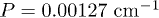 ,
, 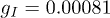 ,
, 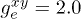 ,
, 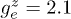 . In this case a typical Zeeman electronic transition in the range of a W-band spectrometer is achieved by a magnetic field of
. In this case a typical Zeeman electronic transition in the range of a W-band spectrometer is achieved by a magnetic field of 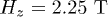 . The main difference to the above treatment is that
. The main difference to the above treatment is that 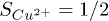 , therefore
, therefore 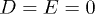 .
.
General scheme
To carry out the algorithm with a magnetic single crystal in an ENDOR setup, the logical quantum circuit needs to be translated into a pulse sequence (fig. 2). Additionally, we need to consider that Quantum Error Correction using the Shor code only makes sense if all allowed transitions at the error step correspond to single-qubit errors. Finally, a mechanism for readout as a final step of the algorithm must be in place. As described below, all three requirements can be met by a proper assignment of spin-qubit labels.
Fig. 2: Top: qubit circuit for a 3-qubit QEC scheme correcting a bit flip error E, part of the Shor code. Bottom: scheme for a pulse sequence between eigenstates (labels correspond to their logical states) highlighting pairs of π-pulses that correspond to a single CNOT gate. See table 1 for the translation between the logical basis and actual wave functions.
Download figure:
Standard imageFor a practical assignment of qubit labels to spin states, it is ideal to separate the six nuclear spin-qubits from the three electronic spin-qubits. The 512 electronuclear states defining our 9 qubits are, however, not necessarily separable, owing to the hyperfine interaction which results in a certain degree of mixing. As a numerical test for this separability, we calculate the fidelity 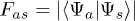 between the (actual) states
between the (actual) states 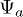 with a given set of parameters and the (simplified) states
with a given set of parameters and the (simplified) states 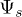 that would result from the cancellation of the hyperfine coupling. As this can change the energy sequence of the different states, for each
that would result from the cancellation of the hyperfine coupling. As this can change the energy sequence of the different states, for each 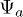 we choose
we choose 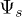 that maximizes Fas. Note that in the case of Tb, the effectively infinite (negative) value of D means that, while we produce
that maximizes Fas. Note that in the case of Tb, the effectively infinite (negative) value of D means that, while we produce 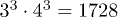 states, we work only with the lowest 512, the other 1206 being beyond our ultraviolet cutoff.
states, we work only with the lowest 512, the other 1206 being beyond our ultraviolet cutoff.
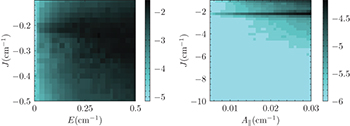
It is interesting to realize that not all of these 512 lowest states are actually needed. The encoded state employs superpositions of all 8 electronic states but only 8 (of 64) nuclear states, resulting in 8 (of 512) electronuclear states. In fact, until the error occurs the full evolution of the system can be described with a mere 22 electronuclear states. Furthermore, with the safe assumption that the error will occur in the electronic part of the system —characterized by faster transitions and shorter decoherence times— the evolution of the system in most experiments will be limited to less than 100 different states. Thus, less than 100 (of 512) different qubit labels are employed from the start to the end of the algorithm. As a conservative estimate, we plotted the bottom of the first quartile (128th highest fidelity). As seen in fig. 3, in both cases the obtained fidelities are very high in ample parameter areas: 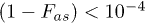 for Tb3+,
for Tb3+,  for Cu2+. This demonstrates the feasibility of the separation of the electronic and nuclear parts of the wave function, and thus the independent assignment of spin-qubit labels. Of course, it would be interesting to systematically explore the robustness of this scheme, estimating the fidelity variation between an ideal case and one with a small deviation in a parameter. While this is outside the scope of this manuscript, sample calculations indicate that the scheme could be moderately robust in this sense: variations of the order of 1 part per 1000 in each one of the parameters has an effect in the lowest fidelity that is well below 1 part per 1000, and commonly below 1 part per 10000. In this sense, the parameter range for the Cu system seems more resilient than the Tb system.
for Cu2+. This demonstrates the feasibility of the separation of the electronic and nuclear parts of the wave function, and thus the independent assignment of spin-qubit labels. Of course, it would be interesting to systematically explore the robustness of this scheme, estimating the fidelity variation between an ideal case and one with a small deviation in a parameter. While this is outside the scope of this manuscript, sample calculations indicate that the scheme could be moderately robust in this sense: variations of the order of 1 part per 1000 in each one of the parameters has an effect in the lowest fidelity that is well below 1 part per 1000, and commonly below 1 part per 10000. In this sense, the parameter range for the Cu system seems more resilient than the Tb system.
Fig. 3: (Color online) Variation of 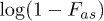 , where Fas is the 128th highest fidelity as a function of the tunneling splitting Δ, the magnetic exchange Jex and the external field Hz. Left: Tb3+ system; right: Cu2+ system (see text).
, where Fas is the 128th highest fidelity as a function of the tunneling splitting Δ, the magnetic exchange Jex and the external field Hz. Left: Tb3+ system; right: Cu2+ system (see text). 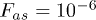 is the precision limit of our calculation.
is the precision limit of our calculation.
Download figure:
Standard imageThe next task is to guarantee that in the encoded state all transitions that are allowed both by spin and by symmetry —the most likely errors— correspond to single-qubit errors and thus are correctable by the Shor code. This is done by a proper assignment of qubit labels to spin states. Table 1 indicates the correspondence of the electronic eigenstates and their qubit values for three effective  (or the lowest part of the spectrum in the case of an S = 1 as discussed above) with a linear connectivity. It was built to guarantee that a) all spin- and symmetry-allowed transitions from the encoded state correspond to single-qubit errors and can thus be corrected and b) the value of the first qubit can be inequivocally read from a measurement determining the absolute value of Ms. Assuming errors will occur in the electronic spin, there are many valid spin-qubit mappings for the nuclear spins.
(or the lowest part of the spectrum in the case of an S = 1 as discussed above) with a linear connectivity. It was built to guarantee that a) all spin- and symmetry-allowed transitions from the encoded state correspond to single-qubit errors and can thus be corrected and b) the value of the first qubit can be inequivocally read from a measurement determining the absolute value of Ms. Assuming errors will occur in the electronic spin, there are many valid spin-qubit mappings for the nuclear spins.
Table 1:. Correspondence between electronic qubits, quantum numbers and wave function. A > a, exact values depending on Jex.
 |
S | Ms | Ψ | |
|---|---|---|---|---|
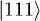 |
1/2 |  |
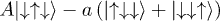 |
|
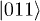 |
1/2 | 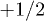 |
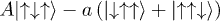 |
|
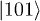 |
1/2 | 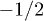 |
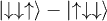 |
|
 |
1/2 | 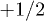 |
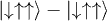 |
|
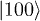 |
3/2 | 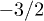 |
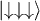 |
|
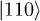 |
3/2 | 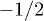 |
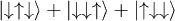 |
|
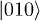 |
3/2 |  |
 |
|
 |
3/2 | 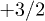 |
 |
|
Experimental considerations
In the last years, the chemical design of single-molecule magnets and molecular spin qubits, including clusters of different nuclearity, has been the hottest topic in molecular magnetism [24,25,29–31]. The exchange interaction in such systems, whether transition metals (superexchange) or lanthanoids (mostly dipolar), can be tuned in strength and sign. Regarding the chemical design of molecules that would be appropiate for this scheme, the versatility of coordination chemistry allows their preparation connected either through covalent bonds (i.e. formation of a discrete molecule) or via supramolecular interactions, such as hydrogen bonds. Figure 1(b) shows a recent example of the covalent class of trimers, but in general the exchange interaction can be controllably weakened from the covalent situation to the supramolecular case, e.g., [{Tb(TETA)}2Tb(H2O)8]+. The case of Cu2+ is much more favourable from the point of view of the electron-nuclear separability but presents some complications, in particular the difficulty to magnetically isolate the trimers from each other. We will center this discussion in the Tb3+ trimer.
As a model lanthanoid system, we study Tb3(OQ)9 (see fig. 1) with the software package SIMPRE [32,33] using an effective point charge model to obtain the ground-state wave function, the tunneling splitting Δ, the gap to the first excited state Ω and gx, gy, gz (table 2). The cases are too many to explore, and thus, as expected, the correspondence to our model Hamiltonian with this particular example is not exact, but the results justify our assumptions in the order of magnitude of the relevant parameters, meaning the same kind of chemistry will be able to produce many similar systems in the same parameter region, with different degrees of aptitude for the present or related scheme. In general, the potential of candidate complexes for these experiments could be estimated by: a) a complex low-energy level scheme determined by continous-wave EPR, with good isolation from the rest of the spectrum and b) the presence of well-resolved pulsed-EPR signals with a sufficiently long relaxation time to allow observing Rabi oscillations.
Table 2:. Single-ion characterization of the Tb+3 ions in Tb3(OQ)9 (see fig. 1): composition of the ground-state wave function, tunneling splitting, gap to the first excited state, anisotropic Landé g-factor. Note that Tb1 and Tb3 are similar but not crystallographically equivalent.
| Ion | 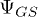 | 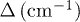 | 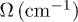 |
gz | gx | gy |
|---|---|---|---|---|---|---|
| Tb1 | 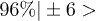 |
0.86 | 89.7 | 17.109 | 0.951 | 1.095 |
| Tb2 | 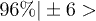 |
0.92 | 191.2 | 17.196 | 0.539 | 0.717 |
| Tb3 | 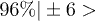 |
1.28 | 83.7 | 16.807 | 0.951 | 1.132 |
In a target system, the initialization to zero, i.e., the preparation of the ground state  , can be achieved by cooling the single crystal at mK temperatures. For the 63Cu2+ systems in parameters explored in this work, hyperfine gaps larger than
, can be achieved by cooling the single crystal at mK temperatures. For the 63Cu2+ systems in parameters explored in this work, hyperfine gaps larger than 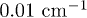 were found, which would make this a viable option. Alternatively, one can work with pseudo-pure states [34,35], as is routinely done in NMR quantum computing setups. Note that the preparation and manipulation of the pseudo-pure state could be implemented using the time-proportional-phase-increment technique, which combines pulses on electron and nuclear spins with waiting times to cancel the off-diagonal term of the density matrix. Special rotation angles need to be applied to the detection pulses in order to distinguish entangled states from superposition states [15]. The realisation of entanglement between the qubits encoded in an electron spin and a nuclear spin has already been reported in an ENDOR experiment using pseudo-pure states [36,37].
were found, which would make this a viable option. Alternatively, one can work with pseudo-pure states [34,35], as is routinely done in NMR quantum computing setups. Note that the preparation and manipulation of the pseudo-pure state could be implemented using the time-proportional-phase-increment technique, which combines pulses on electron and nuclear spins with waiting times to cancel the off-diagonal term of the density matrix. Special rotation angles need to be applied to the detection pulses in order to distinguish entangled states from superposition states [15]. The realisation of entanglement between the qubits encoded in an electron spin and a nuclear spin has already been reported in an ENDOR experiment using pseudo-pure states [36,37].
The "writing" of the non-trivial qubit starting state would then be an arbitrary, coherent transition between the states 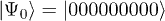 and
and  , i.e. the electron part of the wave function is rotated via three consecutive microwave pulses between
, i.e. the electron part of the wave function is rotated via three consecutive microwave pulses between  and
and 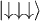 by the desired amount, preserving the nuclear part. Note that the negation of the "target" qubit can be seen as a full transition or π EPR pulse and Hadamard gate is simply a
by the desired amount, preserving the nuclear part. Note that the negation of the "target" qubit can be seen as a full transition or π EPR pulse and Hadamard gate is simply a 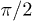 pulse that —for a single qubit— transforms
pulse that —for a single qubit— transforms 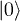 into
into 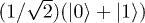 and
and 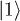 into
into 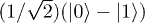 , i.e. transforms "bit" information into "phase" information. Thus, a series of allowed transitions can encode this state either using just the three electronic qubits for the correction of a single error type (fig. 1), or using the nine electronuclear qubits for Shor's QEC code.
, i.e. transforms "bit" information into "phase" information. Thus, a series of allowed transitions can encode this state either using just the three electronic qubits for the correction of a single error type (fig. 1), or using the nine electronuclear qubits for Shor's QEC code.
A complete measurement of the final state of the system can be made simply through a Electron Spin Echo (ESE), i.e. the detection of the standard pulsed EPR signal. Different final states have different ESE spectra, which can be compared with simple states prepared in an independent experiment. If the error is introduced as a controlled operation, all copies of the molecule in the ensemble will share the same state. If the error occurred by itself, the ESE will result in the superposition of the different possibilities, weighted according to each error rate. Interestingly, in the chosen spin-qubit labelling scheme, it is possible to experimentally measure the value of the first qubit just by determining the sign of Ms (i.e. "is the sample attracted or repelled by a given external magnetic field?"). Naturally, this ability to measure and initialize the first qubit can be used, after a series of swap operations, to measure and initialize the ancilla qubits instead. This would preserve the coherent superposition of the first qubit, which is the one that carries the original quantum information, allowing the restart of the quantum error correction procedure.
The full procedure of the Shor code is conceptually simple to derive but experimentally will require the ability to apply pulses of many different frequencies, which can be achieved by an Arbitrary Waveform Generator. Of course, a minimalistic alternative to the full Shor code would be just to use the electrons spins as three qubits for either spin flip or phase flip errors. This could be done with no interference from nuclear states using 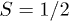 , I = 0 complexes, which can be achieved with either lanthanoids (164Dy, 166Er) or transition metals (low-spin 56Fe3+). More sophisticated alternatives include using electron spins as "bus spins" and nuclear spins as "client qubits", i.e. encoding a quantum state on the electron spin, then transferring it for protection to the nucleus until retrieval is necessary. This approach, which has not yet been implemented in molecular systems, profits from the longer decoherence time of nuclear spins and the faster operation capability of electron spins.
, I = 0 complexes, which can be achieved with either lanthanoids (164Dy, 166Er) or transition metals (low-spin 56Fe3+). More sophisticated alternatives include using electron spins as "bus spins" and nuclear spins as "client qubits", i.e. encoding a quantum state on the electron spin, then transferring it for protection to the nucleus until retrieval is necessary. This approach, which has not yet been implemented in molecular systems, profits from the longer decoherence time of nuclear spins and the faster operation capability of electron spins.
Concluding remarks
In this contribution we explore the possibility of using certain magnetic molecules as dense clusters of electronuclear qubits for Quantum Error Correction. We show that the magnetic coupling between electron spins forces a non-trivial spin-qubit label mapping. Note that always-on coupling is common in the solid state, e.g. NV centers also have always-on hyperfine coupling, thus having tools to deal with it opens new materials as candidate hardware. Exploring a realistic parameter space, we demonstrate that the nuclear part of the spin wave function can be practically decoupled from the electronic part by chemical design, simplifying the implementation of the pulsed EPR experiment. An important advantage of our approach is that it favours non-correlated noise, as we are free to assign the spin-qubit labeling in a way which ensures that transitions flipping more than one qubit are forbidden transitions, and thus statistically unlikely. Hopefully, this work will stimulate further advances in the field of heterogeneous quantum information processing.
Acknowledgments
We thank Joris van Slageren for a crucial comment. The present work has been funded by the EU (ERC Consolidator Grant DECRESIM), the Spanish MINECO (grants CTQ2014-52758-P and CTQ2014-59209-P), and the Generalitat Valenciana (Prometeo and ISIC Programmes of excellence). AG-A and GME acknowledge funding by the MINECO (Ramón y Cajal Program), JJB thanks the Spanish MINECO for an FPU predoctoral grant.
Footnotes
JJB and LE-M did the single-ion work. LE-M and SC-S did the 3- and 9-qubit work. LE-M, JMC-J and GME contributed crucial ideas. JMC-J and LE-M wrote the software. AG-A conceived and supervised the project and wrote the paper. All authors reviewed and contributed to the manuscript.