Abstract
We investigate two vector-soliton–like matter waves collisions in two-component Bose-Einstein condensates with attractive interactions and Gaussian barrier. We present a detailed numerical analysis of the roles of atomic interactions, barrier, relative velocity, and relative phase in collisional dynamics. We show that the interspecies interactions are crucial to make the wave packet propagate as a "breather". We find that the collision-induced trajectory shifts of waves are mainly determined by the intraspecies interactions and proportional to them in the weak nonlinearity regime. Moreover, we explore the meeting time of colliding waves and find it depends on the competition between barrier potential and atomic interactions. Particularly, we study the collisions of two waves with a slight velocity asymmetry (or with different relative phases) and the waves merging and split are demonstrated. The underlying inelastic mechanism closely related to energy exchange is briefly discussed as well.
Export citation and abstract BibTeX RIS
Introduction
Solitons known as localized waves propagating without changing shape and velocity, are a result of a balance between nonlinear interaction and wave packet dispersion. They can be well described by the Korteweg-de Vries (KdV) equation [1] or the nonlinear Schrödinger (NLS) equation. In nonlinear optics, optical solitons refer to peaks (bright) or dips (dark) in the intensity profiles of an optical field [2]. In cold atoms, matter-wave solitons denote peaks or dips in the density profiles of a Bose-Einstein condensate (BEC) [3]. When two individual solitons collide, they pass through one another and emerge from the collision with unaltered form and velocity [4]. However, after the collision a new trajectory reflecting a discontinuous jump is found. In fact, the remarkable trajectory-shift property is owing to the underlying integrability of the one-dimensional (1D) equations [4]. Since the experimental observation of bright solitons in atomic BECs with attractive interatomic interactions [5–7], the dynamics of soliton-like matter waves and their interactions has become an exciting area of research [8,9] due to the potential applications for high-precision interferometry [6,10–14].
The particle-like qualities of solitons including localization, non-dispersion [15], unscathed from collisions with other solitons and with external potentials [14,16], and having center-of-mass trajectories [17–19], bring a good opportunity to investigate the wave-particle duality in a macroscopic scale [20]. On the one hand, bright solitary waves resemble classical particles in their collisional properties [21] and have been extensively studied in both nonlinear optics [22] and BECs. On the other hand, due to the underlying wave nature, a single solitary wave colliding with a potential barrier always reveals partial transmission and reflection as predicted in quantum mechanics [23–25]. This quantum-particle feature suggests a mean-field analog of the famous two-photon Hong-Ou-Mandel (HOM) interference [26] with two bright solitons [27], which makes the direct measurement of both two quantum particles become possible. Additionally, soliton tunneling [28–31] (i.e., scattering of a soliton off finite-size impurities) associated with the nonlinear dynamics of a wave packet colliding with a potential, can be used to illustrate the link between classical and quantum mechanics [20]. However, most of the previous studies in BECs focus on single-component systems, the matter waves interacting with each other or with a potential barrier for two-component BECs have been much less explored.
In this letter, we explore the nature of vector-soliton–like matter waves colliding with a barrier using two-component atomic BECs with attractive interactions. Based on the 1D coupled Gross-Pitaevskii (GP) equations, we numerically study how the atomic interactions (between identical or different bosonic particles) modify the fundamental features of matter-wave collisional dynamics. We further explore the effects of potential barrier on the collisional dynamics. Our main results include three points: i) the existence of interspecies interactions is in favor of "breather" formation during the matter-wave propagation; ii) the interplay between barrier potential and incoherent atomic interactions can provide an effective attractive (or repulsive) interaction between two colliding soliton-like waves which modifies the center-of-mass trajectories and waves meeting time; iii) a slight velocity difference between two colliding waves will prompt waves to merge or split.
Theoretical model
We set two pairs of bright soliton-like matter waves to collide at a narrow barrier of Gaussian form and each pair of waves is associated with each component of two-component BECs. Here the Gaussian barrier can be viewed as a beam splitter in optical experiments. In contrast to a single-component BEC, the cross interactions between two components play a crucial role in wave collision dynamics for two-component system. We consider two-component atomic BECs with attractive interactions and the dynamics can be described by the 1D coupled GP equations. In a normalized form, they are [32]
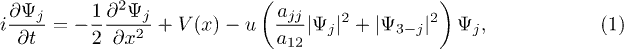
with j = 1 and 2, where ajj and a12 are s-wave scattering lengths of intra- and inter-species atomic collisions, respectively. The interaction constant u is defined by 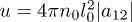 with n0 being the maximum density in the initial distribution of the condensates. The position x, the time t, and the macroscopic wave function
with n0 being the maximum density in the initial distribution of the condensates. The position x, the time t, and the macroscopic wave function  are respectively in units of
are respectively in units of 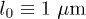 ,
, 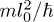 , and
, and 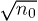 with m being the atom mass.
with m being the atom mass. ![$V(x)=\frac{q}{\sigma\sqrt{2\pi}}\exp[-x^2/(2\sigma^2)]$](https://content.cld.iop.org/journals/0295-5075/111/3/30005/revision1/epl17277ieqn6.gif) denotes a Gaussian barrier with normalized width σ and strength q [25,27]. In general, the coupled equations (1) are not integrable. However, the difference between ajj and a12 in practice is very small and thus in the present study we only concentrate on the case of
denotes a Gaussian barrier with normalized width σ and strength q [25,27]. In general, the coupled equations (1) are not integrable. However, the difference between ajj and a12 in practice is very small and thus in the present study we only concentrate on the case of 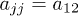 in which the above model amounts to an integrable Manakov system [33,34] when
in which the above model amounts to an integrable Manakov system [33,34] when 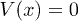 .
.
In order to investigate the dynamics of the matter-wave interactions, initially, we assume that the matter waves take the following soliton-like forms:
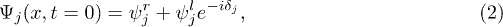
where ![$\psi_j^r(x,t=0)= k_j^r\mathrm{sech}[k_j^r(x+x_r)]e^{iv_rx}$](https://content.cld.iop.org/journals/0295-5075/111/3/30005/revision1/epl17277ieqn9.gif) and
and ![$\psi_j^l(x,t=0)=k_j^l\mathrm{sech}[k_j^l(x-x_l)]e^{-iv_lx}$](https://content.cld.iop.org/journals/0295-5075/111/3/30005/revision1/epl17277ieqn10.gif) . For sufficiently large xl and xr (both xl and xr are positive), eq. (2) approximates a matter-wave solution comprising two bright solitons with unequal amplitudes, kjl and kjr, oppositely moving and unequal velocities, vl and vr, and relative phase
. For sufficiently large xl and xr (both xl and xr are positive), eq. (2) approximates a matter-wave solution comprising two bright solitons with unequal amplitudes, kjl and kjr, oppositely moving and unequal velocities, vl and vr, and relative phase 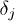 . One can regard the above solutions as two vector-soliton–like waves, which travel in opposite directions with a relative phase
. One can regard the above solutions as two vector-soliton–like waves, which travel in opposite directions with a relative phase 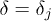 . For convenience we denote them as
. For convenience we denote them as 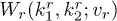 and
and 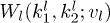 . The subscripts r and l indicate two opposite directions.
. The subscripts r and l indicate two opposite directions.
Subsequently, we explore the interactions of two vector matter waves Wr and Wl with barrier for different parameters 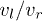 , δ, and u. It is noted that the collisions between Wr and Wl at the barrier strongly depend on the competition between the kinetic energy of the waves and the barrier potential energy. For a lower barrier or a wave packet with higher velocity, the kinetic energy of the incident wave packet is more than the hight of the barrier and thus the wave can easily pass through the barrier, which illustrates a classical transmission scenario. Here we focus our attention on the situation where the velocity of the wave is low enough that the wave packet cannot pass through the barrier in a classical way, i.e.,
, δ, and u. It is noted that the collisions between Wr and Wl at the barrier strongly depend on the competition between the kinetic energy of the waves and the barrier potential energy. For a lower barrier or a wave packet with higher velocity, the kinetic energy of the incident wave packet is more than the hight of the barrier and thus the wave can easily pass through the barrier, which illustrates a classical transmission scenario. Here we focus our attention on the situation where the velocity of the wave is low enough that the wave packet cannot pass through the barrier in a classical way, i.e., 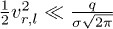 . In our simulations, we choose a finite barrier with height q = 1 and width
. In our simulations, we choose a finite barrier with height q = 1 and width  , the velocity of the right-moving wave, vr, is set to 1, and the velocity of the left-moving wave, vl, can be varied from 0.8 to 1.2. This choice obviously allows us to study the quantum tunneling dynamics in the system.
, the velocity of the right-moving wave, vr, is set to 1, and the velocity of the left-moving wave, vl, can be varied from 0.8 to 1.2. This choice obviously allows us to study the quantum tunneling dynamics in the system.
The interactions between two vector-soliton–like matter waves with Gaussian barrier
We assume that the two vector-soliton–like matter waves, Wl and Wl, are initially located at the positions 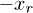 and xl, respectively. Then they propagate in opposite directions and close to each other. To ensure two waves collide exactly at the center of the barrier at x = 0, the condition
and xl, respectively. Then they propagate in opposite directions and close to each other. To ensure two waves collide exactly at the center of the barrier at x = 0, the condition 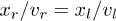 must be satisfied. The numerical simulations are performed by adopting a Fourier pseudospectral split-step method with
must be satisfied. The numerical simulations are performed by adopting a Fourier pseudospectral split-step method with 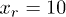 . First we discuss the velocity-symmetry case in which two vector-soliton–like matter waves propagate with identical velocities, i.e.,
. First we discuss the velocity-symmetry case in which two vector-soliton–like matter waves propagate with identical velocities, i.e., 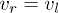 . The time evolution of two matter waves for the first component in this case with different strengths of nonlinearity denoted by the parameter u is demonstrated in fig. 1. It seems that the matter waves maintain the defining property of solitons passing through one another without changing speed, shape, and amplitude [4] in the weak nonlinearity regime (e.g., see fig. 1(a) with
. The time evolution of two matter waves for the first component in this case with different strengths of nonlinearity denoted by the parameter u is demonstrated in fig. 1. It seems that the matter waves maintain the defining property of solitons passing through one another without changing speed, shape, and amplitude [4] in the weak nonlinearity regime (e.g., see fig. 1(a) with 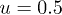 ) with
) with  . However, in the strong nonlinearity regime (e.g., u > 1, see fig. 1(c) and fig. 1(d)), the matter waves propagate like a "breather", which illustrates a periodical change of shape and amplitude with time both before and after the collisions. During the collisions a clear antinode develops at the center of mass (i.e., x = 0), which gives the appearance of an attractive interaction between condensate atoms. Moreover, a jump in the phase of the trajectories of the colliding soliton-like waves is also manifested. The phase jump [35] is shown as a sudden change in position relative to the original trajectory and is mainly determined by the incoherent density-density terms in the GP equations (i.e.,
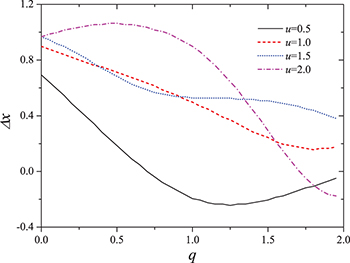
. However, in the strong nonlinearity regime (e.g., u > 1, see fig. 1(c) and fig. 1(d)), the matter waves propagate like a "breather", which illustrates a periodical change of shape and amplitude with time both before and after the collisions. During the collisions a clear antinode develops at the center of mass (i.e., x = 0), which gives the appearance of an attractive interaction between condensate atoms. Moreover, a jump in the phase of the trajectories of the colliding soliton-like waves is also manifested. The phase jump [35] is shown as a sudden change in position relative to the original trajectory and is mainly determined by the incoherent density-density terms in the GP equations (i.e., 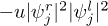 ). Figure 2 shows that the phase jump (or trajectory shift) strongly depends on both the strength of potential barrier and the nonlinearity. The magnitude of the jump in our calculations is found to be proportional to the strength of nonlinearity in the weak nonlinear regime and this is consistent with the estimation given in ref. [4].
). Figure 2 shows that the phase jump (or trajectory shift) strongly depends on both the strength of potential barrier and the nonlinearity. The magnitude of the jump in our calculations is found to be proportional to the strength of nonlinearity in the weak nonlinear regime and this is consistent with the estimation given in ref. [4].
Fig. 1: (Color online) Spatiotemporal distributions of density for the first component (the results for the second component are the same as those for the first one). Two matter waves are set as 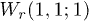 and
and 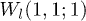 , the relative phase is zero (i.e.,
, the relative phase is zero (i.e., 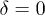 ). (a)
). (a) 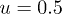 , (b) u = 1, (c)
, (b) u = 1, (c) 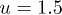 , and (d) u = 2.
, and (d) u = 2.
Download figure:
Standard imageFig. 2: (Color online) Trajectory shifts of solitons vs. the strength of the barrier for different u with 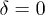 . Two matter waves are set as
. Two matter waves are set as 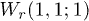 and
and 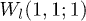 .
.
Download figure:
Standard imageCompared with a single-component BEC, the "breather" behavior in propagation of soliton-like matter waves shown in two-component BECs is a remarkable feature. We explain this as a dramatic effect caused by the presence of attractive interspecies interactions, i.e., 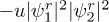 and
and 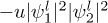 . For
. For 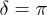 , the matter-wave interference for each component results in a central node structure and this implies that the interactions between two soliton-like waves are effectively repulsive. We stress that in the velocity-symmetry case, either for
, the matter-wave interference for each component results in a central node structure and this implies that the interactions between two soliton-like waves are effectively repulsive. We stress that in the velocity-symmetry case, either for 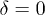 or for
or for 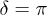 , the matter-wave evolutions for two components (i.e.,
, the matter-wave evolutions for two components (i.e., 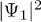 and
and 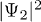 ) are completely synchronized and thus one cannot distinguish them in the space domain.
) are completely synchronized and thus one cannot distinguish them in the space domain.
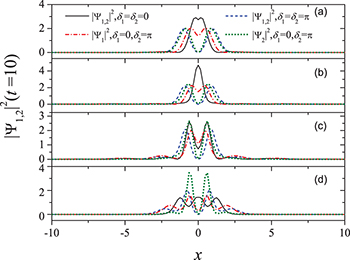
To distinguish the propagating matter waves of two components in the space domain, we consider a typical situation where 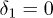 and
and 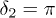 . The interference fringes for each component with different strengths of nonlinearity at t = 10 are shown in fig. 3 (the results for
. The interference fringes for each component with different strengths of nonlinearity at t = 10 are shown in fig. 3 (the results for 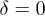 and
and 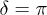 are also given for comparison). A clear difference between the density distributions of
are also given for comparison). A clear difference between the density distributions of  and
and 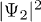 is easily found for the case of
is easily found for the case of 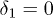 and
and 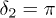 , especially in the strong nonlinear regime (e.g., see fig. 3(d)). In the velocity-symmetry case, as long as
, especially in the strong nonlinear regime (e.g., see fig. 3(d)). In the velocity-symmetry case, as long as 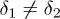 , we can distinguish the density distributions of two components in the space domain. For
, we can distinguish the density distributions of two components in the space domain. For 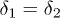 with u = 1 (see fig. 3(b)), a constructive interference leads to a density peak appearing at the center of mass, which indicates an in-phase (i.e.,
with u = 1 (see fig. 3(b)), a constructive interference leads to a density peak appearing at the center of mass, which indicates an in-phase (i.e., 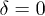 ) collision. Similarly, a destructive interference induces a density node appearing at x = 0 implies an out-of-phase (i.e.,
) collision. Similarly, a destructive interference induces a density node appearing at x = 0 implies an out-of-phase (i.e., 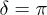 ) collision [4].
) collision [4].
Fig. 3: (Color online) Interference fringes of two soliton-like matter waves for each component at t = 10 with different relative phases. We have set 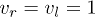 , and
, and 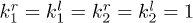 . (a)
. (a) 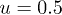 ; (b) u = 1; (c)
; (b) u = 1; (c) 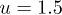 ; and (d) u = 2.
; and (d) u = 2.
Download figure:
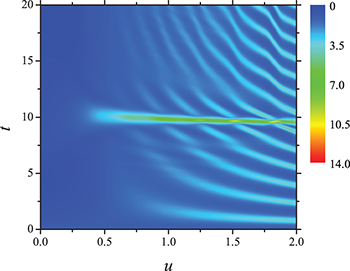
Standard imageIt must be mentioned that the deviations from the fringes of in-phase collision with other nonlinearity strengths (see fig. 3(a), fig. 3(c), and fig. 3(d)) are caused by the existence of the potential barrier. To show the effects of the barrier on the collisional dynamics and interference, we calculate the peak value of the density 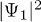 in every moment with different values of u and the results are illustrated in fig. 4. From the peak appearing near t = 10, we find that the time for two colliding waves meeting will be delayed in the weak nonlinearity regime and will be hastened in the strong nonlinearity regime. This can be understood by analyzing the interplay between the barrier potential and the incoherent interactions like the terms
in every moment with different values of u and the results are illustrated in fig. 4. From the peak appearing near t = 10, we find that the time for two colliding waves meeting will be delayed in the weak nonlinearity regime and will be hastened in the strong nonlinearity regime. This can be understood by analyzing the interplay between the barrier potential and the incoherent interactions like the terms 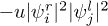 with i = j or
with i = j or  . For a weakly attractive interaction (i.e., u < 1), the barrier provides an effective repulsive interaction between two approaching waves, which is stronger than the attractive atomic interactions and leads to the waves meeting time delay compared with the meeting time obtained without the barrier. On the contrary, for a strongly attractive interaction (i.e., u > 1), the waves will meet ahead of the time estimated without the barrier because the effective repulsive interaction from barrier is weaker than the incoherent attractive interactions between atoms. In fig. 4, an approximately linear relationship between the magnitude of time delay and the nonlinearity u has been demonstrated in the weak nonlinearity regime.
. For a weakly attractive interaction (i.e., u < 1), the barrier provides an effective repulsive interaction between two approaching waves, which is stronger than the attractive atomic interactions and leads to the waves meeting time delay compared with the meeting time obtained without the barrier. On the contrary, for a strongly attractive interaction (i.e., u > 1), the waves will meet ahead of the time estimated without the barrier because the effective repulsive interaction from barrier is weaker than the incoherent attractive interactions between atoms. In fig. 4, an approximately linear relationship between the magnitude of time delay and the nonlinearity u has been demonstrated in the weak nonlinearity regime.
Fig. 4: (Color online) Distributions for the maximum of 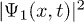 with different u. When t < 10 the maximum is found in the region
with different u. When t < 10 the maximum is found in the region ![$x\in(-\infty,0]$](https://content.cld.iop.org/journals/0295-5075/111/3/30005/revision1/epl17277ieqn45.gif) and when t > 10 the maximum is found in the region
and when t > 10 the maximum is found in the region 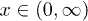 . The parameters are set as
. The parameters are set as 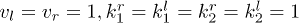 and
and 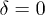 .
.
Download figure:
Standard imageIn the following, we turn to study the situation where two vector-soliton–like matter waves travel with unequal velocities. In this velocity-asymmetry case, a mean-field analog of the HOM interference with bright solitons in a single-component BEC has been revealed in ref. [27]. In our two-component BECs, two vector-soliton–like matter waves will be supposed to play the role of the photon pairs instead of the indistinguishable photons in the HOM experiment setting. The barrier also takes the role of a beam splitter. In this analogy, one can define two normalized integral quantities 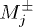 to characterize the total density fraction after colliding with the barrier on each side of space for the j-th component, i.e.,
to characterize the total density fraction after colliding with the barrier on each side of space for the j-th component, i.e.,
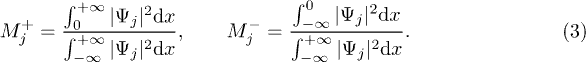
Indeed, each quantity including both reflection and transmission information, can be viewed as a left or a right half-space output in the numerical experiments. Similar to the single-component case, one can easily know that, in the symmetric case (i.e., 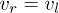 ), two vector-soliton–like incoming matter waves with same parameters will result in
), two vector-soliton–like incoming matter waves with same parameters will result in 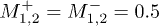 as illustrated in fig. 1. In the asymmetric case with
as illustrated in fig. 1. In the asymmetric case with  , e.g.,
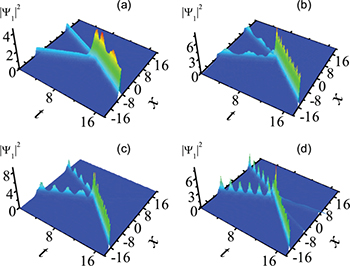
, e.g., 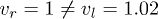 , we give the simulation results of density distributions for two colliding matter waves with different nonlinear interaction strengths in fig. 5. At first glance, we see that an in-phase collision of two soliton-like waves with a barrier can result in a merger (fusion of the wave pair), which show a dramatic deviation from the phenomenon illustrated in the velocity-symmetry case.
, we give the simulation results of density distributions for two colliding matter waves with different nonlinear interaction strengths in fig. 5. At first glance, we see that an in-phase collision of two soliton-like waves with a barrier can result in a merger (fusion of the wave pair), which show a dramatic deviation from the phenomenon illustrated in the velocity-symmetry case.
Fig. 5: (Color online) Spatiotemporal distributions of density for the first component (the results for the second component are the same as those for the first one). Two matter waves are set as 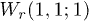 and
and 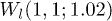 , the relative phase is zero (i.e.,
, the relative phase is zero (i.e., 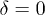 ). (a)
). (a)  , (b) u = 1, (c)
, (b) u = 1, (c) 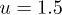 , and (d) u = 2.
, and (d) u = 2.
Download figure:
Standard imageFurthermore, the travelling direction of the composite wave is always in accordance with that of the incident wave with lower speed. In particular, a marked acceleration of the merged wave after collisions is easy to find and its velocity increases with increasing the nonlinear interaction strength u. It is clear that, the outgoing waves from splitting the incoming waves on the barrier are composed of either one (see figs. 5(a) and (b)) or three (see figs. 5(c) and (d)) soliton-like waves. This phenomenon is similar to the birefringence-induced splitting of an initial vector pulse or the formation of the "shadows" in an optical fiber [34,36].
The formation of a strongly localized matter wave after collisions is an intriguing result induced by the inelastic collisions between the waves and the barrier. To exhibit the inelastic process, we have calculated the energy variations of the system during the collisions as displayed in fig. 6 with 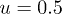 . It is found that the total energy including kinetic energy and potential energy (i.e., potential barrier and nonlinear interactions between particles) before and after the collisions is conserved in the symmetric case, which permits an elastic interaction. However, in the asymmetric case, the total energy after collision decreases. The energy loss implies that there is an exchange between translational energy and internal energy (due to the soliton-like waves merging or split) and thus the collisions are generally inelastic. Obviously, the effective lower potential energy after collisions is constructive to the formation of a strongly localized matter waves.
. It is found that the total energy including kinetic energy and potential energy (i.e., potential barrier and nonlinear interactions between particles) before and after the collisions is conserved in the symmetric case, which permits an elastic interaction. However, in the asymmetric case, the total energy after collision decreases. The energy loss implies that there is an exchange between translational energy and internal energy (due to the soliton-like waves merging or split) and thus the collisions are generally inelastic. Obviously, the effective lower potential energy after collisions is constructive to the formation of a strongly localized matter waves.
Fig. 6: (Color online) Energy variations during the process of matter-wave collisions for the first component with  . The variations for the second component are completely consistent with the first one. We set
. The variations for the second component are completely consistent with the first one. We set 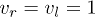 in the symmetric case while set
in the symmetric case while set 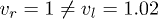 in the asymmetric case. Other parameters are
in the asymmetric case. Other parameters are 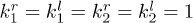 and
and 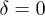 .
.
Download figure:
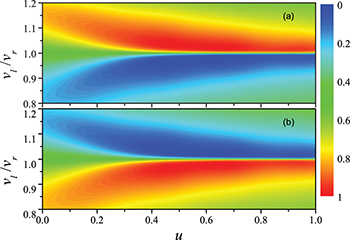
Standard imageNow we explore the roles of velocity asymmetry and nonlinear atomic interactions in the HOM interference. For a fixed 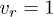 , we calculate
, we calculate 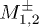 based on eq. (3) with varying vl and u, and the results are given in fig. 7. We see that the peaks occur at the region where
based on eq. (3) with varying vl and u, and the results are given in fig. 7. We see that the peaks occur at the region where 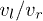 deviates from 1 only a few percent when u > 0.5. This implies that a slight asymmetry in two incident matter waves will lead to a significant asymmetry in spatial distributions for outgoing waves. Moreover, a maximal asymmetry in outputs appears near
deviates from 1 only a few percent when u > 0.5. This implies that a slight asymmetry in two incident matter waves will lead to a significant asymmetry in spatial distributions for outgoing waves. Moreover, a maximal asymmetry in outputs appears near 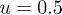 where corresponds to a splitter with nearly equal transmission and reflection. The asymmetry of the outputs decreases rapidly as
where corresponds to a splitter with nearly equal transmission and reflection. The asymmetry of the outputs decreases rapidly as  deviates more significantly from 1 and changes slowly with varying the nonlinearity strength u. In fact, the sensitivity of the asymmetric outgoing matter-wave density distributions on
deviates more significantly from 1 and changes slowly with varying the nonlinearity strength u. In fact, the sensitivity of the asymmetric outgoing matter-wave density distributions on 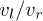 in the vicinity of 1 is induced by the phase difference between two incoming waves accumulated before interacting with the barrier. In our case, this phase difference can be estimated by
in the vicinity of 1 is induced by the phase difference between two incoming waves accumulated before interacting with the barrier. In our case, this phase difference can be estimated by 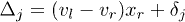 for the j-th component. From fig. 7, we obtain
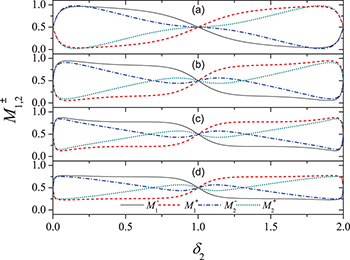
for the j-th component. From fig. 7, we obtain  . From this perspective, one can control the asymmetry of outgoing waves by setting deferent initial relative phases between two incoming waves with equal speed. To this end, we fix
. From this perspective, one can control the asymmetry of outgoing waves by setting deferent initial relative phases between two incoming waves with equal speed. To this end, we fix 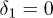 and only change
and only change 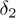 from 0 to
from 0 to 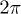 and calculate the quantities
and calculate the quantities 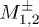 with different nonlinearity strengths. As shown in fig. 8, we find that the peaks symmetrically appear at the positions near
with different nonlinearity strengths. As shown in fig. 8, we find that the peaks symmetrically appear at the positions near 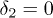 and
and 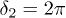 , which are in consistent with the above theoretical predictions for slight velocity difference. Comparing the outputs for two components, we find that the asymmetry for the first component is sensitive to the relative phase
, which are in consistent with the above theoretical predictions for slight velocity difference. Comparing the outputs for two components, we find that the asymmetry for the first component is sensitive to the relative phase  in the regions near 0, π, or
in the regions near 0, π, or 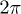 , while for the second component it is sensitive to
, while for the second component it is sensitive to  in the regions near 0 or
in the regions near 0 or 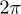 . Furthermore, both the maximal asymmetries and the corresponding relative phases are different for two components. This suggests one can identify the spatial distribution symmetries of two components by different strengths with the help of tuning initial relative phase between two incident waves of one component. It is clear that the symmetry in outgoing wave packets increases (i.e., the peak values reduce) as the nonlinear interactions increase.
. Furthermore, both the maximal asymmetries and the corresponding relative phases are different for two components. This suggests one can identify the spatial distribution symmetries of two components by different strengths with the help of tuning initial relative phase between two incident waves of one component. It is clear that the symmetry in outgoing wave packets increases (i.e., the peak values reduce) as the nonlinear interactions increase.
Fig. 7: (Color online) Variations of (a) 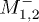 and (b)
and (b) 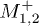 vs.
vs. 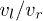 with different u. The parameters are chosen as
with different u. The parameters are chosen as  , and
, and 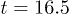 .
.
Download figure:
Standard imageFig. 8: (Color online) Profiles of 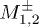 vs.
vs. 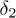 (in units of π) with
(in units of π) with 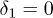 . Other parameters are same as those in fig. 7. (a)
. Other parameters are same as those in fig. 7. (a)  , (b) u = 1, (c)
, (b) u = 1, (c) 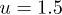 , (d) u = 2.
, (d) u = 2.
Download figure:
Standard imageConclusion
In summary, we have presented a general and detailed numerical analysis of the collisions between two vector-soliton–like matter waves at a narrow Gaussian potential barrier in two-component atomic BECs with attractive atomic interactions. In this coupled system the nonlinear interactions between condensate atoms can divide into two types: the intraspecies interactions and the interspecies interactions. It is shown that the roles of two types interactions in the matter-waves propagating dynamics are very different. The attractive intraspecies interactions corresponding to the nonlinear terms in the focusing NLS equations, are crucial to form soliton-like localized matter waves by compensating for wave packets dispersions. The attractive interspecies interactions are found to be inclined to broaden the wave packets. Together, the two complementary interactions permit the wave packet moving as a "breather" with both amplitude and width varying periodically with time. This phenomenon illustrates a distinctive difference of solitary waves propagation between single-component BEC and two-component BECs.
When two soliton-like matter waves collide at the barrier, three important features should be emphasized. First, similar to the case without barrier, the collision-induced trajectory shift given as a sudden change in position relative to the original trajectory is also demonstrated, which is mainly determined by the nonlinear interactions between coherent atoms in different wave packets and its magnitude is estimated to be proportional to the strength of nonlinearity in the weak nonlinear regime. Second, the existence of the barrier during the collisions will change the colliding waves meeting time due to the competition between the barrier potential and the nonlinear interactions between different wave packets. Third, in the velocity-symmetry case a symmetric incoming wave will lead to a symmetric outgoing wave for each component while in the velocity-asymmetry case a symmetric input will result in an asymmetric output owing to the inelastic collisions. In particular, the latter process gives a good analogy of the HOM interference experiment and this process can be easily controlled by adjusting the relative phase between two incoming waves. Our present studies elucidate the roles of mean-field interactions, potential barrier, relative velocity, and relative phase in vector-soliton–like matter-waves collisions. Additionally, the collision in the presence of the potential barrier may help to generate entanglement of semi-classical solitons [37,38]. In experiments, both 85Rb-133Cs mixtures [37] and different hyperfine states in 7Li [39] could be promising candidate two-component systems for the observation of our theoretical predictions due to the advanced experimental techniques available in the fields of atomic and optical physics [40].
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Grant No. 11305120, No. 11275145, No. 91021021, and No. 11005055), the Natural Science Fundamental Research Program of Shaanxi Province of China (Grant No. 2015JQ1017), and the Fundamental Research Funds for the Central Universities of China.