Abstract
We investigate the teleportation of a qubit between two observers Alice and Bob in an asymptotically flat Robertson-Walker expanding spacetime. We use scalar or fermionic field modes inside Alice's and Bob's ideal cavities and show the degradation of the teleportation quality, as measured by the fidelity, through a mechanism governed by spacetime expansion. This reduction is demonstrated to increase with the rapidity of the expansion and to be highly sensitive to the coupling of the field to spacetime curvature, becoming considerably stronger as it reduces from conformal to minimal. We explore a perturbative approach in the cosmological parameters to compute the Bogoliubov coefficients in order to evaluate and compare the fidelity degradation of fermionic and scalar fields.
Export citation and abstract BibTeX RIS
As quantum technologies progress and cutting-edge experiments incorporate relativistic regimes, studying the effects of gravity and motion on these technologies becomes increasingly more important. Consequently, relativistic aspects of quantum information theory in both flat and curved spacetimes have been extensively studied [1]. A good example is quantum metrology, which uses quantum properties of probes to measure precision observables such as time [2], field strengths [3], gravity waves [4], Unruh temperatures [5], effects of gravity on entanglement using Bose-Einstein condensates [6], Schwarzschild parameters of the Earth [7], etc. From the theoretical standpoint, the study of effective models such as quantum field theory on curved spacetime [8] has been revisited with an eye towards both estimating and understanding quantum metrology and quantum information protocols [9].
Quantum teleportation is a fundamental tool for the transmission of quantum information [10,11] where a sender (Alice) aims to transmit an unknown state to the receiver (Bob) without sending the system itself, which is thus never transported between the two sites during teleportation. However, a small amount of classical information must be telegraphed between the two sites, preventing quantum teleportation from being instantaneous which is in accordance with special relativity. A nice account of relativistic effects on quantum teleportation can be found in [12].
Besides the issues of creating and maintaining long-distance entanglement, it is a matter of paramount importance in quantum information protocols to understand the interplay between quantum nonlocality and relativistic locality, and space-like correlations and causality. In [13], the quantum fidelity of a teleported state between two moving cavities in relativistic motion (Alice at rest and Bob uniformly accelerated) was computed in order to study how fidelity is degraded by the Unruh effect. Moreover, the Unruh effect is used in [14] to investigate the teleportation of quantum states when one of the entangled qubits used in the process is under the influence of some external force, which leads to the sudden death of entanglement and teleportation fidelity loss. Scalar, fermionic and vector fields in accelerated cavities were discussed in [15].
In [16,17] it was suggested that information on the underlying spacetime can be recovered from the entanglement of scalar/fermionic field modes. It would be interesting to investigate such idea in the context of a quantum information task, for instance, in the analysis of the fidelity in quantum teleportation in an expanding spacetime. Moreover, entanglement plays a crucial role in quantum information protocols, and the study of its degradation/creation mechanisms in dynamical spacetimes is important [13,18,19].
In the present work we investigate the effect on quantum teleportation of entanglement frame dependence in a general relativistic setting, in the context of an expanding, asymptotically flat Robertson-Walker (RW) spacetime. For the sake of generality we explore both fermions and scalar field modes. For the latter we consider a non-minimal coupling to 4-dimensional spacetime since there may occur substantial differences between minimal and conformal coupling [9]. Assuming that the metric is flat in both the distant past and future, we consider for this purpose the following gedankenexperiment: at the distant Minkowskian past, two comoving observers Alice and Bob share a maximally entangled, EPR Bell state 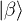 . It is a Bell state of qubits, encoded in terms of the modes of a real massive scalar field or of a fermionic field. Each observer uses an isolated, non-interacting ideal cavity capable of supporting such field modes to maintain the qubit in his/her possession. Furthermore, Alice holds an extra ideal cavity with a qubit superposition state that she wants to teleport to Bob within the standard protocol T0 of Bennett et al. (also called the BBCJPW protocol) [10], using the Bell state
. It is a Bell state of qubits, encoded in terms of the modes of a real massive scalar field or of a fermionic field. Each observer uses an isolated, non-interacting ideal cavity capable of supporting such field modes to maintain the qubit in his/her possession. Furthermore, Alice holds an extra ideal cavity with a qubit superposition state that she wants to teleport to Bob within the standard protocol T0 of Bennett et al. (also called the BBCJPW protocol) [10], using the Bell state 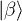 as a quantum channel. If the teleportation protocol is performed when Alice and Bob are in the distant past, then the corresponding fidelity of course is maximal. But instead, the experiment we describe consists of Alice waiting to perform the teleportation task only in the distant future, after spacetime expansion saturates (evidently, the roles of Alice and Bob may be exchanged, as they are both comoving observers).
as a quantum channel. If the teleportation protocol is performed when Alice and Bob are in the distant past, then the corresponding fidelity of course is maximal. But instead, the experiment we describe consists of Alice waiting to perform the teleportation task only in the distant future, after spacetime expansion saturates (evidently, the roles of Alice and Bob may be exchanged, as they are both comoving observers).
In our gedankenexperiment, we rely on the single-mode approximation (SMA) —namely, on the fact that the local physics in the cavity is well described by a single mode of the extended field. Such SMA was shown not to hold in general in the case of the study of field mode entanglement degradation for observers moving in relative uniform acceleration [20]. Apart from some peculiarities with fermion modes, their results beyond SMA are argued to be qualitatively equivalent to SMA. For the sake of simplicity, we shall therefore rely on the SMA approximation, although a generalization beyond SMA for teleportation in RW spacetimes would be interesting.
We will show that in this case the fidelity of teleportation reduces from the point of view of Bob as the degree of entanglement of the Bell state 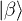 degrades due to spacetime expansion. We study how these reductions are influenced by the coupling of the scalar field to the scalar curvature of spacetime, and discuss how they are affected by the rapidity of the expansion. We will also extend the results to the case of the teleportation of fermions and explore how the fidelity is affected by the bosonic or fermionic character of the fields.
degrades due to spacetime expansion. We study how these reductions are influenced by the coupling of the scalar field to the scalar curvature of spacetime, and discuss how they are affected by the rapidity of the expansion. We will also extend the results to the case of the teleportation of fermions and explore how the fidelity is affected by the bosonic or fermionic character of the fields.
The period of spacetime expansion affects the degree of entanglement of the quantum channel  because it implies particle creation: under the above assumptions, Bob perceives Alice receding away from him in his local inertial frame as the experiment proceeds, and for him the vacuum state inside Alice's cavity becomes a particle-populated, thermal state in the distant future. We proceed to describe and quantify this creation process.
because it implies particle creation: under the above assumptions, Bob perceives Alice receding away from him in his local inertial frame as the experiment proceeds, and for him the vacuum state inside Alice's cavity becomes a particle-populated, thermal state in the distant future. We proceed to describe and quantify this creation process.
In conformal coordinates the metric reads
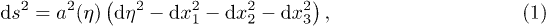
where a is the scale factor characterizing the expansion and η is the conformal time, related to Alice's proper time t by  . The dynamics over the spacetime described by eq. (1) of a real non-interacting scalar field ϕ with mass m coupled to gravity is given by the covariant form of the Klein-Gordon equation,
. The dynamics over the spacetime described by eq. (1) of a real non-interacting scalar field ϕ with mass m coupled to gravity is given by the covariant form of the Klein-Gordon equation,

where ξ is the coupling of the field to the Ricci scalar curvature R and □ is the covariant D'Alambertian. The cases  and
and  correspond to minimal and conformal coupling to gravity, respectively. Therefore, the field equation (2) in the conformal coordinates
correspond to minimal and conformal coupling to gravity, respectively. Therefore, the field equation (2) in the conformal coordinates 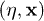 and in terms of an auxiliary field variable
and in terms of an auxiliary field variable  reduces to
reduces to
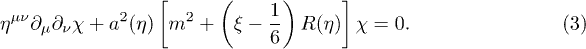
Let as assume a scale factor of the form 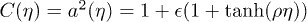 , where the rate of spacetime expansion is given by the parameter
, where the rate of spacetime expansion is given by the parameter 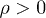 and the total amount of expansion by
and the total amount of expansion by  . Then
. Then 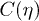 conveniently represents a spacetime that undergoes a period of smooth expansion and becomes flat in the distant past
conveniently represents a spacetime that undergoes a period of smooth expansion and becomes flat in the distant past 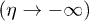 and in the far future
and in the far future 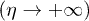 , namely
, namely 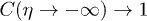 and
and 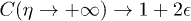 . In these two asymptotic regions, the in region
. In these two asymptotic regions, the in region 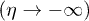 and the out region
and the out region  , there is a time-like Killing vector field
, there is a time-like Killing vector field 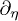 such that
such that 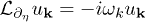 for some
for some 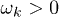 , where
, where 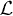 denotes the Lie derivative. Hence, we can define particle states in each of these regions in terms of positive frequency modes, as well as a vacuum state. Treating
denotes the Lie derivative. Hence, we can define particle states in each of these regions in terms of positive frequency modes, as well as a vacuum state. Treating 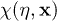 as a field operator, we can express
as a field operator, we can express 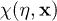 in the in region (respectively, out region) as a combination of positive frequency
in the in region (respectively, out region) as a combination of positive frequency 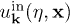 and negative frequency
and negative frequency 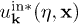 solutions (respectively,
solutions (respectively, 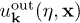 and
and 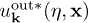 ) to eq. (3):
) to eq. (3):
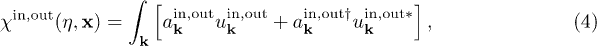
where 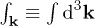 , and
, and  (respectively,
(respectively, 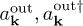 ) are annihilation/creation operators characterizing the in-vacuum
) are annihilation/creation operators characterizing the in-vacuum 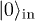 (respectively, out-vacuum
(respectively, out-vacuum 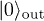 ) state of the field, subject to the usual commutation relations. From the values of C(η) at
) state of the field, subject to the usual commutation relations. From the values of C(η) at 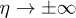 , where the Ricci scalar is
, where the Ricci scalar is 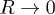 , the mode function solutions to eq. (3) are
, the mode function solutions to eq. (3) are
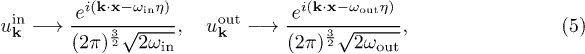
for 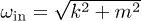 ,
, 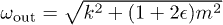 , and
, and 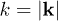 .
.
The relationship between in and out modes is given by a Bogoliubov transformation,
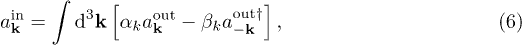
mixing only modes of the same momentum, where the (Bogoliubov) coefficients are determined by the scalar product of mode functions: 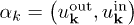 and
and 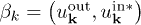 . The corresponding relation between the in and out vacua is
. The corresponding relation between the in and out vacua is
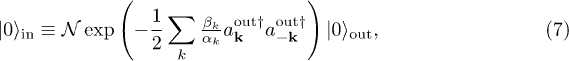
where 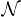 is a normalization factor. It shows that the in-vacuum is a two-mode squeezed out-vacuum state, which implies in particular that the out-region number operator
is a normalization factor. It shows that the in-vacuum is a two-mode squeezed out-vacuum state, which implies in particular that the out-region number operator 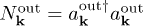 has a positive in-vacuum expectation value
has a positive in-vacuum expectation value 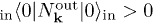 in the Heisenberg picture, which describes the dynamical creation of particles from the vacuum in Alice's cavity from Bob's point of view.
in the Heisenberg picture, which describes the dynamical creation of particles from the vacuum in Alice's cavity from Bob's point of view.
We thus see that, for Bob, an initial vacuum state inside Alice's cavity 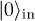 becomes populated with particles in the asymptotic future
becomes populated with particles in the asymptotic future  , which is just the right-hand side of (7) at
, which is just the right-hand side of (7) at  . After some algebra in eq. (7), we get
. After some algebra in eq. (7), we get
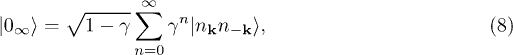
where 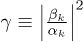 . Similarly, the one-particle excitation in the in-vacuum
. Similarly, the one-particle excitation in the in-vacuum 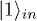 evolves as
evolves as 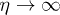 into the state
into the state 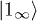 given in terms of out-region Fock states by
given in terms of out-region Fock states by

In what follows, we will need therefore to have the explicit value of Bogoliubov coefficients. To obtain it, let us begin by noticing that spatial translation invariance allows us to express the mode functions for the field equation in the form 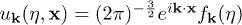 , in which
, in which 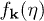 satisfies
satisfies
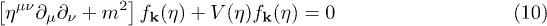
for 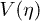 given by
given by
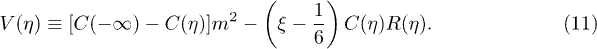
Following [8,21], observing that 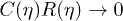 as
as  if
if  and
and 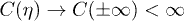 as
as 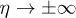 if
if 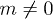 , we may treat
, we may treat 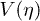 as small to solve eq. (10) by iteration to the lowest order in
as small to solve eq. (10) by iteration to the lowest order in 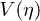 in terms of the momentum space propagator. Using (5) as initial condition, the solution
in terms of the momentum space propagator. Using (5) as initial condition, the solution 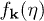 of (10) is given by the following convolution integral involving the retarded propagator:
of (10) is given by the following convolution integral involving the retarded propagator:
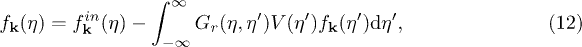
which satisfies ![$\left[\eta^{\mu\nu}\partial_{\mu}\partial_{\nu} + m^2\right]G_{r}(\eta,\eta') = \delta(\eta - \eta')$](https://content.cld.iop.org/journals/0295-5075/111/6/60001/revision1/epl17385ieqn65.gif) and in momentum space it reads
and in momentum space it reads
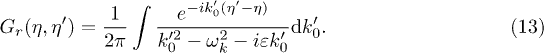
The momentum integral can be performed by closing the integration contour in the upper-half complex momentum plane. However, for the calculation of the Bogoliubov coefficients, it suffices to notice that in the limit 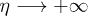 ,
, 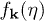 can be written in terms of the in-mode functions as
can be written in terms of the in-mode functions as ![$f_{\mathbf{k}}(\eta) \longrightarrow (2\omega)^{-\frac{1}{2}}[\alpha_{k}e^{-i\omega\eta} + \beta_{k}e^{i\omega\eta}]$](https://content.cld.iop.org/journals/0295-5075/111/6/60001/revision1/epl17385ieqn68.gif) , where
, where 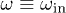 . Taking this into (12) yields the following expressions for the Bogoliubov coefficients:
. Taking this into (12) yields the following expressions for the Bogoliubov coefficients:
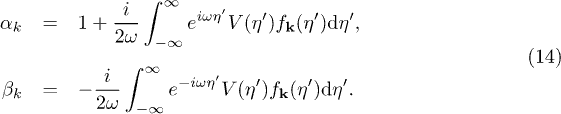
Assuming the conditions that justify a perturbative solution, eq. (14) allows us to calculate 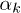 and
and 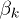 to lowest order in
to lowest order in  . To leading order
. To leading order  , which together with eq. (11) gives
, which together with eq. (11) gives

The integrals in (15) can be easily evaluated in the complex plane by replacing the real variable η by the complex variable z and integrating around a closed counterclockwise rectangular contour Σ with vertices at 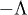 , Λ,
, Λ, 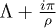 ,
, 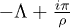 . In the upper horizontal path we use that
. In the upper horizontal path we use that 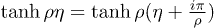 . The two vertical paths parallel to the imaginary axis vanish exponentially as
. The two vertical paths parallel to the imaginary axis vanish exponentially as 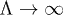 . For the first term in eq. (15), we have
. For the first term in eq. (15), we have
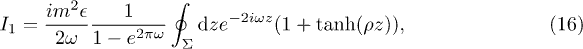
whose integrand has a pole at 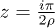 . Using Cauchy's integral formula we find
. Using Cauchy's integral formula we find ![$I_{1} =m^2\epsilon \pi [ 2\omega\rho \sinh(\pi\omega{\rho}^{-1})]^{-1}$](https://content.cld.iop.org/journals/0295-5075/111/6/60001/revision1/epl17385ieqn80.gif) .
.
The second term in eq. (15) can be evaluated in a similar way. The resulting expression for  is
is
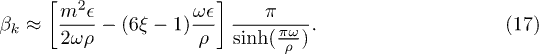
The calculation of the Bogoliubov coefficient  is analogous and to this order
is analogous and to this order 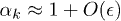 .
.
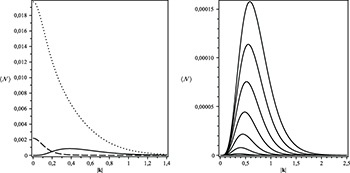
Notice that this calculation also shows how the particle number seen by Bob inside Alice's cavity relates to the coupling of the field to the scalar curvature. The spectral behaviour of particle number for different values of ξ is summarized in fig. 1. In particular, for 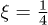 the generation due to spacetime expansion of bosonic particles reproduces the behavior of fermions [16].
the generation due to spacetime expansion of bosonic particles reproduces the behavior of fermions [16].
Fig. 1: Particle number as a function of k for different values of the 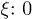 (dotted line), 1/6 (dashed line) and 1/4 (solid line) with
(dotted line), 1/6 (dashed line) and 1/4 (solid line) with 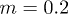 ,
, 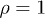 , and
, and 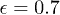 (left) and for different expansion parameter
(left) and for different expansion parameter 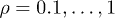 with
with 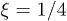 (right), where we have fixed
(right), where we have fixed 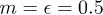 .
.
Download figure:
Standard imageSuppose that Alice's and Bob's cavities support the orthogonal modes 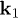 ,
, 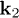 of frequency
of frequency 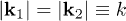 of ϕ, labeled, respectively, as Ai and Bi,
of ϕ, labeled, respectively, as Ai and Bi, 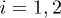 . Assume that the Bell state
. Assume that the Bell state 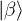 shared by Alice and Bob in the distant past is the maximally entangled, EPR Bell state
shared by Alice and Bob in the distant past is the maximally entangled, EPR Bell state
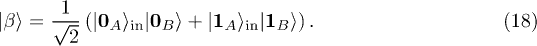
The states 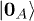 and
and 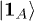 are defined in terms of the dual-rail basis as suggested in [13],
are defined in terms of the dual-rail basis as suggested in [13], 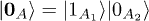 ,
,  , with similar expression for Bob's cavity (in Bob's local frame, the in and out modes are the same and therefore the subscript "in" will be omitted). Then, it follows from the previous considerations that in the distant future, after spacetime expansion saturates, the state in Alice and Bob's possession will no longer be
, with similar expression for Bob's cavity (in Bob's local frame, the in and out modes are the same and therefore the subscript "in" will be omitted). Then, it follows from the previous considerations that in the distant future, after spacetime expansion saturates, the state in Alice and Bob's possession will no longer be 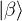 ; instead, it will be the mixed state
; instead, it will be the mixed state

which we obtain by tracing the negative momenta 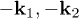 degrees of freedom out of Bob's party in
degrees of freedom out of Bob's party in 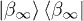 , where
, where
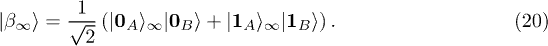
Here, we defined 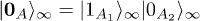 and
and 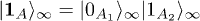 , following the notation introduced in eqs. (8), (9).
, following the notation introduced in eqs. (8), (9).
The mixed state 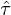 is still an entangled state and may be used to perform the teleportation of a qubit superposition state from Alice to Bob. However, it is no longer a maximally entangled state. In fact, a direct computation shows that the logarithmic negativity of
is still an entangled state and may be used to perform the teleportation of a qubit superposition state from Alice to Bob. However, it is no longer a maximally entangled state. In fact, a direct computation shows that the logarithmic negativity of 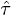 is given in terms of γ by
is given in terms of γ by
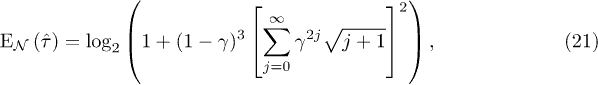
which attains the upper bound 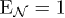 only in the limit
only in the limit 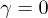 when there is no particle creation inside Alice's cavity due to spacetime expansion.
when there is no particle creation inside Alice's cavity due to spacetime expansion.
This reduction of the degree of entanglement of the quantum channel results in degradation of the fidelity of teleportation. In order to compute the fidelity, assume that Alice has an additional cavity containing the qubit superposition state 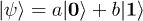 . This state is unknown to Bob. The full input state is
. This state is unknown to Bob. The full input state is 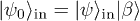 . If Alice made a Bell measurement on her two qubits in the distant past with the result
. If Alice made a Bell measurement on her two qubits in the distant past with the result  ,
, 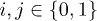 , then after Alice's measurement the full state would be projected into
, then after Alice's measurement the full state would be projected into

where the final state received by Bob would be
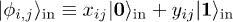
with four possible conditional state amplitudes given by 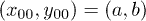 ,
, 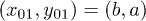 ,
, 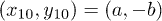 ,
, 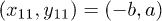 . However, when Alice makes the Bell measurement in the distant future, the final state received by Bob would be obtained by tracing the
. However, when Alice makes the Bell measurement in the distant future, the final state received by Bob would be obtained by tracing the 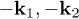 degrees of freedom out of
degrees of freedom out of
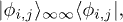
where 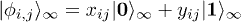 . Explicitly, this state is
. Explicitly, this state is
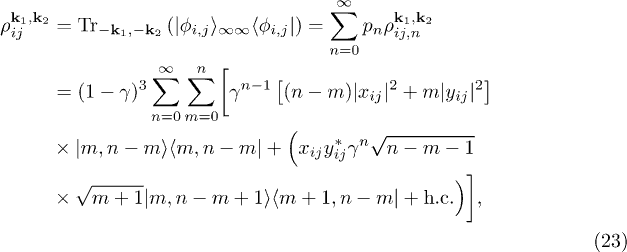
where  ,
,  , and
, and  .
.
The teleportation will be complete only when Bob receives from Alice the classical information  concerning the result of her measurement and applies a unitary transformation to verify the protocol in his local frame. Notice that this will be feasible as long as Alice and Bob remain causally connected as
concerning the result of her measurement and applies a unitary transformation to verify the protocol in his local frame. Notice that this will be feasible as long as Alice and Bob remain causally connected as 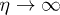 (smooth expansion)1
. From eq. (23), we obtain the fidelity corresponding to the teleportation,
(smooth expansion)1
. From eq. (23), we obtain the fidelity corresponding to the teleportation,
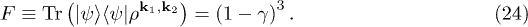
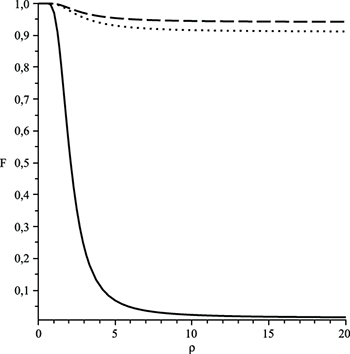
This result, together with the results found for the Bogoliubov coefficients, allows us to determine the influence of spacetime expansion on the protocol. It suggests that even a small disturbance in conformal symmetry results in degradation of the quality of the teleportation. In fact, it is only under conformal symmetry that there is no particle creation due to spacetime expansion and no response on the logarithmic negativity of the quantum teleportation channel and on the fidelity F. A numerical study of (24) shows that the fidelity of teleportation always degrades due to conformal symmetry breaking (non-zero mass or/and non-conformal coupling).
Moreover, for  , as the coefficient ξ increases from minimal to conformal, the fidelity increases. Concerning the role played by the parameters of the expansion, we find that the rapidity ρ of the expansion leads to a reduction of the fidelity, but only up to a threshold. If the expansion is too fast (large ρ), the fidelity and logarithmic negativity are not affected. Our analysis is summarized in fig. 2. Because the creation of high-mass and high
, as the coefficient ξ increases from minimal to conformal, the fidelity increases. Concerning the role played by the parameters of the expansion, we find that the rapidity ρ of the expansion leads to a reduction of the fidelity, but only up to a threshold. If the expansion is too fast (large ρ), the fidelity and logarithmic negativity are not affected. Our analysis is summarized in fig. 2. Because the creation of high-mass and high  modes particles demands a larger amount of energy from spacetime expansion, only low
modes particles demands a larger amount of energy from spacetime expansion, only low 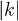 modes significantly contribute to fidelity degradation.
modes significantly contribute to fidelity degradation.
Fig. 2: Fidelity as a function of the expansion parameter ρ for the bosonic field case with minimal coupling (solid line) and conformal coupling (dotted line). The dashed line shows the fidelity for the fermionic case. We have fixed 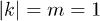 and
and 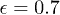 . The logarithmic negativity has a similar behavior.
. The logarithmic negativity has a similar behavior.
Download figure:
Standard imageLet us extend our considerations to the teleportation of fermionic modes to assess the effect of the Grassman character of the field on the teleportation fidelity. For this purpose consider a Dirac spinless field of mass m. In this case, it can be shown [22] that the relation between the in- and out-region vacua is
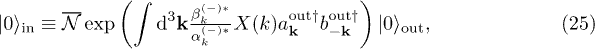
where 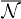 is a normalization constant,
is a normalization constant, 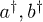 denote creation operators for particles and antiparticles, respectively, and X(k) is the polarization tensor given by
denote creation operators for particles and antiparticles, respectively, and X(k) is the polarization tensor given by
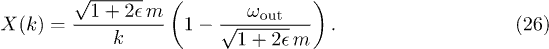
The Bogoliubov coefficients can also be found in a perturbative approach. The result is identical to the scalar case, save that 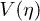 is substituted with
is substituted with
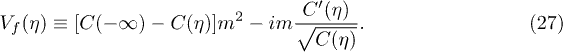
Following the notation used in [16,22] we redefine  and
and 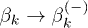 . The resulting expression for
. The resulting expression for 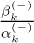 is
is
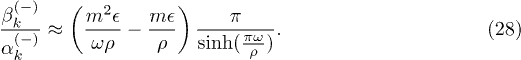
This result coincides to leading order in  in which
in which 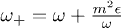 and
and 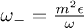 , with
, with 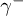 obtained in [16]. After some algebra in (25), we verify that
obtained in [16]. After some algebra in (25), we verify that 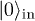 evolves in the asymptotic future into the following state in terms of particle and antiparticle modes:
evolves in the asymptotic future into the following state in terms of particle and antiparticle modes:
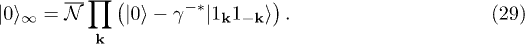
Notice that due to the Pauli exclusion principle the number of fermionic excitations is limited to {1, 0}. Similarly, the 1-particle excitation state in the in region evolves into

The experiment can be considered along the same lines as for the scalar field case. A dual rail basis state can be interpreted in terms of particle excitations in one of two possible spatial modes in Alice's or Bob's cavity. Assuming they shared a Bell state of the same form as in eq. (18) in the distant past, the entangled state  available to perform the teleportation at
available to perform the teleportation at  would result from tracing out the antiparticle degrees of freedom out of Alice's party. It would have the same form shown in eqs. (19), (20) but with the expressions (29) and (30) for the evolved Fock states. The resulting logarithmic negativity and fidelity of teleportation are found to be
would result from tracing out the antiparticle degrees of freedom out of Alice's party. It would have the same form shown in eqs. (19), (20) but with the expressions (29) and (30) for the evolved Fock states. The resulting logarithmic negativity and fidelity of teleportation are found to be
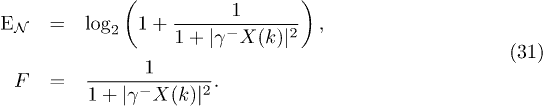
The numerical analysis of the expression shows that the reduction of the fidelity in the present case is qualitatively similar to the conformally coupled bosonic case. This is a consequence of the already observed fact that the generation of bosonic particles for 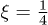 is equivalent to the generation of fermionic particles, which can also be traced back to the fact that the Dirac equation in curved spacetime can be written as a Klein-Gordon–type equation with a non-minimal coupling to gravity and covariant derivatives.
is equivalent to the generation of fermionic particles, which can also be traced back to the fact that the Dirac equation in curved spacetime can be written as a Klein-Gordon–type equation with a non-minimal coupling to gravity and covariant derivatives.
Acknowledgments
HA and MS acknowledge financial support from CNPq. PM acknowledges support from STFC under the consolidated Grants ST/J000426/1 and ST/L000407/1. His research is also supported in part by the Marie Curie network GATIS (gatis.desy.eu) of the European Union's Seventh Framework Programme FP7/2007-2013/ under REA Grant Agreement No. 317089.
Footnotes
- 1
It is noteworthy to mention that if Alice makes the measurement in the distant past but Bob waits until the distant future before receiving Alice's message and applying the relevant unitary, then she does not need to remain in causal contact; in this case, all is needed is that he gets the measurement's result before falling out of causal contact. The results one would obtain for the fidelity under this setup are however the same.