Export citation and abstract BibTeX RIS
In a recent letter, Sun et al. [1] have studied a self-dual quasiperiodic tight-binding model, obtained by extending the well-known Aubry-André (AA) model with a second-harmonic potential, as well as with next-nearest neighbor hoppings. Unexpectedly, in spite of the self-duality the authors show, by numerical calculations for the golden-mean irrationality, the existence of mobility edges in the spectrum, and conclude that "generally all of the self-dual QP models including far neighbors provide the mobility edges". This is particularly surprising, not only because it is in contrast with the AA model, but even more because it is in apparent contrast with the results of ref. [2], whose authors, in 1991, studied exactly the same model, and gave numerical evidence, from studies of a bronze-mean irrationality, for an energy-independent metal-insulator transition, and consequently no mobility edges. The main point of this Comment is to illustrate that the apparent contradiction between the results of refs. [1] and [2] is rooted in a subtle dependence on the properties of the chosen irrational number, and how it connects to the heuristic generalization of the Thouless formula given in ref. [2]. We also point out some apparently incorrect statements in ref. [1].
First, we must emphasize that, although the authors of ref. [1] repeatedly in their letter propose their model as "a new type of self-dual quasiperiodic model", ref. [2] (co-authored by the present author) proposed exactly the same model 25 years ago. Equations (2), (3) of ref. [1] are equivalent to eqs. (7), (8) of ref. [2], and the self-duality conditions of ref. [1] are the same as eq. (9) of ref. [2]. Curiously enough, even the specific choice of the ratio between next-nearest- and nearest-neighbor couplings (which for self-duality must be the same as the ratio between the second-harmonic and fundamental potential terms),  with the notation of ref. [1], is the same as in ref. [2]. It must also be mentioned that the energy dependence of the localization length in the localized regime of the model, also presented as a "new" result in ref. [1], was already obtained in ref. [2], too (see sect. III and fig. 3 in ref. [2]).
with the notation of ref. [1], is the same as in ref. [2]. It must also be mentioned that the energy dependence of the localization length in the localized regime of the model, also presented as a "new" result in ref. [1], was already obtained in ref. [2], too (see sect. III and fig. 3 in ref. [2]).
Thus, if results in ref. [1] should be of general validity, they must be consistent with results of ref. [2]. The only essential difference between the parameter values used in the numerical calculations of refs. [1] and [2] is the choice of irrationality: while ref. [1] used the golden mean 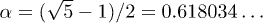 , ref. [2] had chosen the bronze mean
, ref. [2] had chosen the bronze mean  . (The general definition of the "precious means" is
. (The general definition of the "precious means" is ![$\alpha(\mu)=[(\mu^2+4)^{1/2}-\mu]/2$](https://content.cld.iop.org/journals/0295-5075/112/1/17002/revision1/epl17419ieqn4.gif) , see, e.g., eqs. (10)–(12) of ref. [2].) Still, the results are strikingly different. Figure 2 in ref. [2] shows that, with very little doubt, all eigenstates of the infinite chain are extended for
, see, e.g., eqs. (10)–(12) of ref. [2].) Still, the results are strikingly different. Figure 2 in ref. [2] shows that, with very little doubt, all eigenstates of the infinite chain are extended for 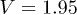 and localized for
and localized for 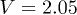 , and there are no mobility edges in the spectrum (here, the potential strength V corresponds to λ of ref. [1]). By contrast, figs. 1, 2 and 4 in ref. [1] show that, equally convincingly, there is a large interval of potential strenghts
, and there are no mobility edges in the spectrum (here, the potential strength V corresponds to λ of ref. [1]). By contrast, figs. 1, 2 and 4 in ref. [1] show that, equally convincingly, there is a large interval of potential strenghts  with one or several mobility edge(s) in the spectrum (with the exception of the fixed point of the duality transformation
with one or several mobility edge(s) in the spectrum (with the exception of the fixed point of the duality transformation  where all states are critical, as observed also in ref. [2]). Here, by duality,
where all states are critical, as observed also in ref. [2]). Here, by duality, 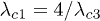 , and judging from figs. 1 and 4 in ref. [1],
, and judging from figs. 1 and 4 in ref. [1],  and
and  . The authors of ref. [1] also claim that they "observed qualitatively the same localization-delocalization transition" both for the silver mean and bronze mean, where the latter would obviously contradict the results of ref. [2].
. The authors of ref. [1] also claim that they "observed qualitatively the same localization-delocalization transition" both for the silver mean and bronze mean, where the latter would obviously contradict the results of ref. [2].
Apparently, the only way in which the novel results in ref. [1] can be reconciled with the old results of ref. [2] must be that the qualitative nature of the localization-delocalization transition essentially depends on the choice of irrationality, where (at least for the particular coupling ratio 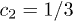 ) the golden mean yields mobility edges while the bronze mean yields an energy-independent metal-insulator transition at
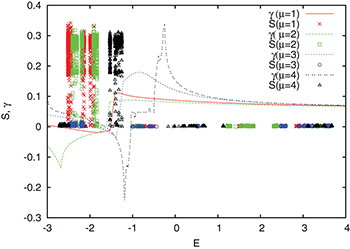
) the golden mean yields mobility edges while the bronze mean yields an energy-independent metal-insulator transition at 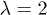 . That this is indeed the case is illustrated in fig. 1, where we, analogously to fig. 2 in ref. [2], have plotted the standard deviation S for all eigenstates
. That this is indeed the case is illustrated in fig. 1, where we, analogously to fig. 2 in ref. [2], have plotted the standard deviation S for all eigenstates 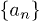 vs. eigenenergy at
vs. eigenenergy at  , for the first four precious means with different symbols. As usual, S is defined from the second moment,
, for the first four precious means with different symbols. As usual, S is defined from the second moment, ![$S^2=\frac{1}{N^2}[\sum n^2 |a_n|^2-(\sum n |a_n|^2) ^2]$](https://content.cld.iop.org/journals/0295-5075/112/1/17002/revision1/epl17419ieqn22.gif) , and, for large N, S typically takes values between 0.18 and 0.29 for extended states in a lattice with fixed boundary conditions, while
, and, for large N, S typically takes values between 0.18 and 0.29 for extended states in a lattice with fixed boundary conditions, while 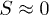 for localized states [2]. As can be seen, even though
for localized states [2]. As can be seen, even though 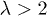 the lowest-energy bands are indeed extended for the golden and silver means, in agreement with ref. [1] using the inverse participation ratio (IPR), while for the bronze mean all states are localized in agreement with [2]. For the fourth precious mean
the lowest-energy bands are indeed extended for the golden and silver means, in agreement with ref. [1] using the inverse participation ratio (IPR), while for the bronze mean all states are localized in agreement with [2]. For the fourth precious mean 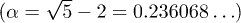 , there are in fact two mobility edges, with localized states at the lowest energies as well as for all positive energies, and a regime of extended states for
, there are in fact two mobility edges, with localized states at the lowest energies as well as for all positive energies, and a regime of extended states for 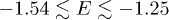 .
.
Fig. 1: (Color online) Symbols: standard deviation S vs. eigenenergy E for eigenstates of eq. (2) in ref. [1] with 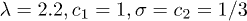 , and α given by precious means with different μ according to the legend. Fixed boundary conditions were used for chains of N = 4095 sites. Lines: the evaluation of the expression (27) in ref. [2] for the characteristic exponent
, and α given by precious means with different μ according to the legend. Fixed boundary conditions were used for chains of N = 4095 sites. Lines: the evaluation of the expression (27) in ref. [2] for the characteristic exponent 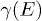 for the corresponding parameter values, for
for the corresponding parameter values, for  (red solid line),
(red solid line),  (green dashed line),
(green dashed line), 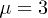 (blue dotted line), and
(blue dotted line), and 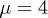 (black double-dotted line), respectively.
(black double-dotted line), respectively.
Download figure:
Standard imageSome understanding for the origin of the qualitatively different behaviors for different incommensurabilities can be obtained from the heuristic generalization of the Thouless formula discussed in ref. [2]. In the case of the standard AA model, the Thouless formula combined with duality yields the celebrated expression for the energy-independent characteristic exponent (inverse localization length) 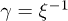 of eigenstates in the localization regime,
of eigenstates in the localization regime, 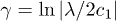 with the notation of ref. [1]. Using analogous (non-rigorous) arguments for the self-dual model with next-nearest-neighbor interactions was shown to yield an additional, energy-dependent correction term to the AA expression, which could be evaluated numerically from the iteration of a four-dimensional linear map (see eqs. (24), (26) and (27) in ref. [2]). As noted in ref. [2], this correction term could be either positive or negative, and thus the localization length could, depending on the eigenenergy, be either smaller or larger than the corresponding AA length. However, in fact the correction term could also for some energies E be negative with a magnitude larger than
with the notation of ref. [1]. Using analogous (non-rigorous) arguments for the self-dual model with next-nearest-neighbor interactions was shown to yield an additional, energy-dependent correction term to the AA expression, which could be evaluated numerically from the iteration of a four-dimensional linear map (see eqs. (24), (26) and (27) in ref. [2]). As noted in ref. [2], this correction term could be either positive or negative, and thus the localization length could, depending on the eigenenergy, be either smaller or larger than the corresponding AA length. However, in fact the correction term could also for some energies E be negative with a magnitude larger than  , in which case eq. (27) in ref. [2] would give a negative value for the characteristic exponent. This would indicate that the assumptions of having
, in which case eq. (27) in ref. [2] would give a negative value for the characteristic exponent. This would indicate that the assumptions of having 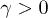 for
for  and
and  for
for  , used to obtain eq. (27) in ref. [2], would break down for these energies. Instead, for such energies one should apply the more general eq. (26) in ref. [2], which then by duality gives a finite, positive localization length at
, used to obtain eq. (27) in ref. [2], would break down for these energies. Instead, for such energies one should apply the more general eq. (26) in ref. [2], which then by duality gives a finite, positive localization length at  , for an eigenstate at energy
, for an eigenstate at energy 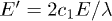 , if the state at energy E at
, if the state at energy E at 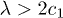 is assumed to be extended with
is assumed to be extended with 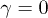 .
.
We illustrate this by plotting the expression 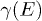 , obtained from eq. (27) in ref. [2] for
, obtained from eq. (27) in ref. [2] for 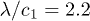 by numerical iterations of eq. (24) in ref. [2] until convergence, with different line types in fig. 1 for the four first precious means. Note that although the numerical iteration gives a well-defined value
by numerical iterations of eq. (24) in ref. [2] until convergence, with different line types in fig. 1 for the four first precious means. Note that although the numerical iteration gives a well-defined value 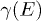 for any E, the interpretation as an inverse localization length is evidently only valid for energies inside the spectrum (which for
for any E, the interpretation as an inverse localization length is evidently only valid for energies inside the spectrum (which for  is expected to have positive measure for
is expected to have positive measure for  , like the standard AA model). It is clear from fig. 1, that the regimes of extended states for
, like the standard AA model). It is clear from fig. 1, that the regimes of extended states for  correspond exactly to those energies in the spectrum where the numerical evaluation of
correspond exactly to those energies in the spectrum where the numerical evaluation of  becomes negative. Moreover, we see that also for
becomes negative. Moreover, we see that also for 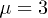 there is a narrow interval
there is a narrow interval 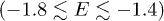 where
where 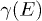 becomes negative; however, this interval lies entirely inside a major gap
becomes negative; however, this interval lies entirely inside a major gap  , which thus explains why there are no extended states, and consequently no mobility edges, in the spectrum for the bronze mean.
, which thus explains why there are no extended states, and consequently no mobility edges, in the spectrum for the bronze mean.
In conclusion, we have resolved the apparent contradiction between the earlier results [2] claiming an energy-independent metal-insulator transition, and the new results [1] claiming the general existence of mobility edges, for the self-dual model with next-nearest-neighbor interactions. Using a generalized version of Thouless formula from ref. [2], an energy-independent metal-insulator transition is seen to appear only for such irrationals where there is no overlap between the energy spectrum and the regime where the formula gives negative values for the characteristic exponent. We hope that pointing out this subtle dependence on the properties of the irrational number will stimulate further, more rigorous work on the topic.