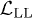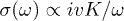Abstract
We study the edge transport in two-dimensional topological insulators which is carried by interacting helical fermions. This transport is ballistic when it is protected by time-reversal symmetry. Recently it was pointed out (Altshuler B. L. et al., Phys. Rev. Lett., 111 (2013) 086401) that coupling of non-interacting helical electrons to an array of randomly anisotropic magnetic (Kondo) impurities can lead to a spontaneous breaking of the symmetry and, thus, can remove this protection. By using a combination of the functional and the Abelian bosonization approaches, we show that the suppression of the ballistic transport turns out to be robust in a broad range of the interaction strength. We have evaluated the renormalization of the localization length and have found that, for strong interaction, it is substantial. We have identified various regimes of the dc transport and discussed its temperature and sample size dependences in each of the regimes.
Export citation and abstract BibTeX RIS
Introduction
Electron transport in time-reversal invariant topological insulators (TI) has become a hot topic of research during several past years, see refs. [1–4] for reviews. The bulk electron states in the TIs are gapped, nevertheless, dc transport is possible since it is provided by low-dimensional helical edge modes. Helicity means the lock-in relation between electron spin and momentum: helical electrons propagating in opposite directions have opposite spins [5,6]. An elastic backscattering of a helical electron must be accompanied by a spin-flip. Therefore, the helical electrons are immune to effects of potential disorder such as localization.
Recent experimental studies of the charge transport through 1D channels at the helical edges of 2D TIs [7–10] made of quantum wells [11,12] demonstrated that the transport is indeed close to be ballistic as long as the samples are small [7,13]. However, longer edges exhibit lower conductance [7,8,14] which is evidence for backscattering. Moreover, the absence of clear temperature dependence of the sub-ballistic conductance in a broad temperature interval [15] suggests that this backscattering is probably elastic.
Robustness of the ballistic transport in the TIs was discussed in several theoretical papers. Spin-flips needed for the backscattering could be, for example, due to spin-(1/2) Kondo impurities. However, the Kondo screening of the spin would recover the ballistic transport at low temperatures [16,17]. The inelastic processes caused by interactions in the presence of disorder are predicted to result in temperature-dependent contributions to the dc conductance and conductance fluctuations [18–22]. Such corrections are also frozen out at cooling due to the lack of the phase space. Thus, the explanation of the dc transport in the TIs, which i) is non-ballistic at low temperatures, and ii) can be temperature independent, remains a theoretical challenge.
The first step toward the understanding of the non-ballistic temperature-independent transport through 1D helical edges was taken in ref. [23] where the idea of spontaneous breaking of time-reversal symmetry was proposed. It was demonstrated that helical 1D electrons, which do not interact with each other, are localized at zero temperature if they are coupled to an array of the Kondo impurities. This coupling can be described by the Hamiltonian
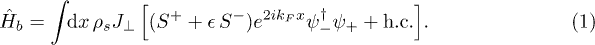
Here  describes spin-up right-moving (spin-down left-moving) in the x-direction helical fermions
describes spin-up right-moving (spin-down left-moving) in the x-direction helical fermions 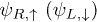 ; kF is the Fermi momentum; ρs is the impurity density;
; kF is the Fermi momentum; ρs is the impurity density;  is the coupling constant between the Kondo and the fermion spins;
is the coupling constant between the Kondo and the fermion spins;  is the parameter of the anisotropy in the XY-plane (plane of TI);
is the parameter of the anisotropy in the XY-plane (plane of TI); 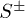 are the Kondo spin operators.
are the Kondo spin operators.
For isotropic couplings,  , the indirect interaction between spins induces a slowly varying in space and time spin polarization. Homogeneous time-independent polarization would create a gap,
, the indirect interaction between spins induces a slowly varying in space and time spin polarization. Homogeneous time-independent polarization would create a gap,  , in the spectrum of fermions (
, in the spectrum of fermions ( is the impurity spin). Fluctuations of the polarization result in heavy but gapless "polaronic" complexes of helical electrons dressed by slow spinons. These complexes are charged and can support ballistic transport with a strongly reduced Drude weight. A random anisotropy,
is the impurity spin). Fluctuations of the polarization result in heavy but gapless "polaronic" complexes of helical electrons dressed by slow spinons. These complexes are charged and can support ballistic transport with a strongly reduced Drude weight. A random anisotropy, 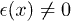 , quenches the local spin polarization and causes spontaneous symmetry breaking. The polaronic complexes lose their protection from the backscattering and undergo the Anderson localization with localization length
, quenches the local spin polarization and causes spontaneous symmetry breaking. The polaronic complexes lose their protection from the backscattering and undergo the Anderson localization with localization length  .
.
In this letter, we explore the charge localization and transport in the system of interacting helical electrons, helical Luttinger liquid (HLL), coupled to the array of the Kondo impurities. Motivated by recent experiments, we study the dc transport in finite samples in different temperature regimes; this topic has not been addressed in ref. [23]. In particular, we identify those regimes where the conductance could be below its ballistic value remaining (almost) temperature independent, cf. ref. [15].
Interactions in the HLL are characterized by the Luttinger parameter 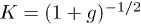 (g is the dimensionless interaction strength). We prove that the moderate attraction, 1 < K < 2, and (almost) arbitrary repulsion, K < 1, do not change the qualitative picture of the non-interacting system: the effective theory, which describes localization in the HLL coupled to the Kondo array, remains valid, though the gap, Δ, and the localization radius,
(g is the dimensionless interaction strength). We prove that the moderate attraction, 1 < K < 2, and (almost) arbitrary repulsion, K < 1, do not change the qualitative picture of the non-interacting system: the effective theory, which describes localization in the HLL coupled to the Kondo array, remains valid, though the gap, Δ, and the localization radius,  , are substantially renormalized:
, are substantially renormalized:

Here EB is the UV energy cutoff which is of the order of the bulk gap in the TI.
The energy scales which govern different temperature regimes of the dc transport are sketched in fig. 1. They are the temperature of the many-body localization transition [24], TMBL, and the depinning energy, Epin, defined below, see eq. (16). We will assume that  (see footnote 1
); see the discussion after eq. (16).
(see footnote 1
); see the discussion after eq. (16).
Fig. 1: (Color online) Sketch of the temperature dependence of the dc conductivity in different regimes, see explanations in the section "DC transport".
Download figure:
Standard imageIf 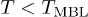 all excitations are localized and ballistic transport is suppressed. If
all excitations are localized and ballistic transport is suppressed. If  , the dc conductivity is finite albeit low and is of a quantum nature. The transport becomes thermally activated as
, the dc conductivity is finite albeit low and is of a quantum nature. The transport becomes thermally activated as  and turns into a semiclassical one in the interval
and turns into a semiclassical one in the interval  . Power-law dependences of
. Power-law dependences of  at
at  result from the interaction-dependent renormalization of
result from the interaction-dependent renormalization of  , see eqs. (17), (18).
, see eqs. (17), (18).
Model and calculations
The Hamiltonian of the HLL coupled to the array of the Kondo impurities is  , where the first two terms describe the free fermions and the interaction between them, respectively:
, where the first two terms describe the free fermions and the interaction between them, respectively:
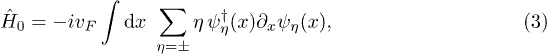
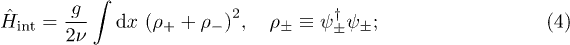
here vF is the Fermi velocity and ν is the density of states in the HLL. The backscattering term  (caused by the coupling of the electrons to the Kondo impurities) is defined in eq. (1). We neglect the forward-scattering term
(caused by the coupling of the electrons to the Kondo impurities) is defined in eq. (1). We neglect the forward-scattering term  since a unitary transformation of the Hamiltonian allows one to map the model with the parameters
since a unitary transformation of the Hamiltonian allows one to map the model with the parameters  to its counterpart with the effective Luttinger parameter
to its counterpart with the effective Luttinger parameter  and
and  [25,26]. Thus,
[25,26]. Thus,  takes into account both the direct electron-electron interaction and the interaction mediated by the z-coupling to the Kondo impurities.
takes into account both the direct electron-electron interaction and the interaction mediated by the z-coupling to the Kondo impurities.
The tendency to the spin ordering [23] allows us to develop a path integral formulation of the problem using the parametrization of each spin by its azimuthal angle, α, and projection on the z-axis,  ; τ denotes the imaginary time. It is convenient to use the spins rotation:
; τ denotes the imaginary time. It is convenient to use the spins rotation:  which leads to the redefinition of the anisotropy parameter:
which leads to the redefinition of the anisotropy parameter:  . For a high density of the Kondo array with a weak irregularity in positions of the spin impurities, the model can be simplified by treating ρs and
. For a high density of the Kondo array with a weak irregularity in positions of the spin impurities, the model can be simplified by treating ρs and  as random variables: real
as random variables: real  and complex
and complex  . Fluctuations of ρs do not affect the dc transport in the HLL, cf. ref. [23], thus, one can use the averaged density. On the contrary, randomness of
. Fluctuations of ρs do not affect the dc transport in the HLL, cf. ref. [23], thus, one can use the averaged density. On the contrary, randomness of  plays the crucial role. Without loss of generality,
plays the crucial role. Without loss of generality,  can be treated as a Gaussian random function with zero mean value and short-range correlations
can be treated as a Gaussian random function with zero mean value and short-range correlations

As a result, the Lagrangian density for the HLL coupled to the Kondo array can be presented as

here  ;
;  are the chiral derivatives;
are the chiral derivatives;  is the fermionic spinor field. Further calculations are based on the scale separation: the fermionic variables are much faster than the spin ones. Therefore, as will be verified below,
is the fermionic spinor field. Further calculations are based on the scale separation: the fermionic variables are much faster than the spin ones. Therefore, as will be verified below,
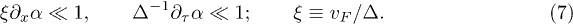
To describe the composite fermion-spinon excitations, we perform a gauge transformation of the fermionic fields  ; the Lagrangian acquires the form
; the Lagrangian acquires the form
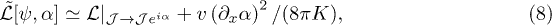
where  is the renormalized velocity, and subleading terms
is the renormalized velocity, and subleading terms  are neglected in
are neglected in  due to eq. (7).
due to eq. (7).
We start the analysis of the electron interaction effects with the zero anisotropy case,  . The classical configuration of the spin variables is
. The classical configuration of the spin variables is  ,
,  . Our goal is to derive an effective theory describing fluctuations around the classical solution. For g = 0, this is achieved by integrating out all massive modes: firstly, the fermions with the gap
. Our goal is to derive an effective theory describing fluctuations around the classical solution. For g = 0, this is achieved by integrating out all massive modes: firstly, the fermions with the gap  , and, secondly, the variable nz (in the quadratic approximation). The interaction can be taken into account with the help of the functional bosonization, which involves the Hubbard-Stratonovich decoupling of the interaction term and the gauge transformation of the fermionic fields [27,28]. Following these standard steps, one can show that the main non-perturbative effect of the weak interaction is the renormalization of the backscattering amplitude, which acquires an effective energy dependence,
, and, secondly, the variable nz (in the quadratic approximation). The interaction can be taken into account with the help of the functional bosonization, which involves the Hubbard-Stratonovich decoupling of the interaction term and the gauge transformation of the fermionic fields [27,28]. Following these standard steps, one can show that the main non-perturbative effect of the weak interaction is the renormalization of the backscattering amplitude, which acquires an effective energy dependence,  . Similarly to the bare relation
. Similarly to the bare relation  , we introduce the renormalized gap at each step of the renormalization procedure:
, we introduce the renormalized gap at each step of the renormalization procedure:

Equation (9) has been obtained after neglecting small and slow spatial fluctuations in  and
and  and it is valid only provided that
and it is valid only provided that  . The renormalization stops when
. The renormalization stops when  becomes smaller than Δ since the fermions become massive. Accordingly, the effective fermionic gap
becomes smaller than Δ since the fermions become massive. Accordingly, the effective fermionic gap  can be determined from the self-consistency equation:
can be determined from the self-consistency equation:  , which leads to the result given in eq. (2) for attractive, 1 < K < 2, or weakly repulsive,
, which leads to the result given in eq. (2) for attractive, 1 < K < 2, or weakly repulsive,  interactions. However, this straightforward way of calculations needs justification because multiparticle scatterings are generated. It is difficult to analyze their relevance within the functional bosonization approach. To justify the self-consistent derivation of
interactions. However, this straightforward way of calculations needs justification because multiparticle scatterings are generated. It is difficult to analyze their relevance within the functional bosonization approach. To justify the self-consistent derivation of  and to analyze the case of stronger repulsion, we use an alternative approach realized by bosonizing fermions:
and to analyze the case of stronger repulsion, we use an alternative approach realized by bosonizing fermions:
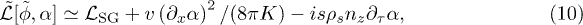
where at 
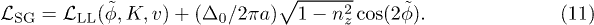
Here ![${\cal L}_{\text{LL}}(\tilde{\phi},K,v)\equiv[(\partial_\tau \tilde{\phi})^2 + (v\partial_x \tilde{\phi})^2]/(2\pi Kv)$](https://content.cld.iop.org/journals/0295-5075/112/5/57003/revision1/epl17568ieqn59.gif) ;
;  is the smallest spatial scale;
is the smallest spatial scale;  is a composite phase:
is a composite phase:  , with ϕ being the usual bosonic phase, its gradient is related to the fermionic density:
, with ϕ being the usual bosonic phase, its gradient is related to the fermionic density:  [29].
[29].
Similarly to eq. (8), sub-leading gradients of α are neglected in eq. (10). This can be justified since 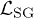 corresponds to the quantum sine-Gordon model where the relevant vertex
corresponds to the quantum sine-Gordon model where the relevant vertex  generates the bosonic mass at K < 2 resulting in the scale separation between bosonic and spin degrees of freedom. If K > 2, this vertex becomes irrelevant because a strong attraction of the helical fermions leads to superconducting correlations which suppress the backscattering by the Kondo impurities. The effective gap Δ in the spectrum of bosons can be determined by using the Feynman variational method [29]. After neglecting fluctuations of nz, the gap equation reads
generates the bosonic mass at K < 2 resulting in the scale separation between bosonic and spin degrees of freedom. If K > 2, this vertex becomes irrelevant because a strong attraction of the helical fermions leads to superconducting correlations which suppress the backscattering by the Kondo impurities. The effective gap Δ in the spectrum of bosons can be determined by using the Feynman variational method [29]. After neglecting fluctuations of nz, the gap equation reads

Equation (12) is valid at  for K < 2, i.e., for arbitrary strong repulsion and for weak and moderate attraction2
. The multiparticle backscattering, which is described by (less relevant) higher vertices
for K < 2, i.e., for arbitrary strong repulsion and for weak and moderate attraction2
. The multiparticle backscattering, which is described by (less relevant) higher vertices ![$\sim D^{(n)}\cos\,[2n{\tilde \phi}]$](https://content.cld.iop.org/journals/0295-5075/112/5/57003/revision1/epl17568ieqn67.gif) in
in  ,
,  , can be included into the gap equation. Such vertices yield corrections to the RHS of eq. (12) of order
, can be included into the gap equation. Such vertices yield corrections to the RHS of eq. (12) of order  . We assume that
. We assume that  . To ensure that all higher vertices generate only sub-leading corrections to the gap equation, we request
. To ensure that all higher vertices generate only sub-leading corrections to the gap equation, we request  and solve this inequality at
and solve this inequality at  , where (with logarithmic accuracy)
, where (with logarithmic accuracy)  and
and  , see eq. (12). This results in the condition
, see eq. (12). This results in the condition  which allows us to neglect the multiparticle backscattering.
which allows us to neglect the multiparticle backscattering.
For weak and moderate interactions,  , the bosonic gap Δ and the fermionic one
, the bosonic gap Δ and the fermionic one  coincide. This equivalence can be extended to the case of the strong repulsion where sub-leading terms in eq. (9) become important3
. After justifying the self-consistent derivation of the gap we insert into eq. (8) renormalized quantities (the effective gap Δ, the effective velocity v, and the factor
coincide. This equivalence can be extended to the case of the strong repulsion where sub-leading terms in eq. (9) become important3
. After justifying the self-consistent derivation of the gap we insert into eq. (8) renormalized quantities (the effective gap Δ, the effective velocity v, and the factor  in the gradient term) instead of their bare values. Simultaneously, we neglect g in the first term of
in the gradient term) instead of their bare values. Simultaneously, we neglect g in the first term of 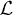 and restore the anisotropy. We use the gap Δ in further calculations since it allows us to describe the strong repulsion.
and restore the anisotropy. We use the gap Δ in further calculations since it allows us to describe the strong repulsion.
Integrating out the massive variables, we obtain
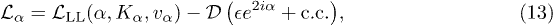

where  . At K = 1, eqs. (13), (14) are equivalent to the results of ref. [23]. The fermion-spinon excitations (see Introduction) are slow in the absence of the interactions,
. At K = 1, eqs. (13), (14) are equivalent to the results of ref. [23]. The fermion-spinon excitations (see Introduction) are slow in the absence of the interactions,  . As K decreases, the ratio
. As K decreases, the ratio  increases remaining small as long as
increases remaining small as long as  . Inequality
. Inequality  reflects the scale separation between the interacting (fast) helical fermions and the (slow) composite quasiparticles. Equation (13) is valid at K < 2, therefore
reflects the scale separation between the interacting (fast) helical fermions and the (slow) composite quasiparticles. Equation (13) is valid at K < 2, therefore 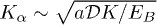 is small with and without interactions.
is small with and without interactions.
DC transport
A regular anisotropy,  , would pin the phase,
, would pin the phase,  . The pining is similar to the effect of a magnetic field applied in the XY-plane: it breaks time-reversal symmetry and opens a global gap in the spectrum of the composite quasiparticles trivially blocking the ballistic dc transport.
. The pining is similar to the effect of a magnetic field applied in the XY-plane: it breaks time-reversal symmetry and opens a global gap in the spectrum of the composite quasiparticles trivially blocking the ballistic dc transport.
Random fluctuations of  , eq. (5), prevent the opening of the global gap but are able to localize the composite quasiparticles at
, eq. (5), prevent the opening of the global gap but are able to localize the composite quasiparticles at  . Indeed, eq. (13) describes a disordered Sine-Gordon model where quasiparticles are localized [30]. Since
. Indeed, eq. (13) describes a disordered Sine-Gordon model where quasiparticles are localized [30]. Since  , the localization length can be evaluated by the usual optimization procedure [29]:
, the localization length can be evaluated by the usual optimization procedure [29]:  is defined as a spatial scale on which the typical energy governed by the last term in eq. (13) (i.e., the potential energy of the disorder) becomes equal to the energy governed by the term
is defined as a spatial scale on which the typical energy governed by the last term in eq. (13) (i.e., the potential energy of the disorder) becomes equal to the energy governed by the term  in
in  (i.e., Epin). This yields
(i.e., Epin). This yields

Let us discuss different temperature regimes of the dc transport. The localization strongly affects the dc transport in not too short samples, 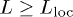 , at
, at  : the conductance is resistive (finite but smaller than the ballistic one) and temperature-independent in transient samples with
: the conductance is resistive (finite but smaller than the ballistic one) and temperature-independent in transient samples with  , and the conductance vanishes in long samples,
, and the conductance vanishes in long samples,  .
.
Sizable dc transport in long samples  appears only at higher temperatures: if
appears only at higher temperatures: if  , the fermions are still gapped but many-body states become delocalized and are able to support weak dc quantum transport similar to transport in glassy systems. As
, the fermions are still gapped but many-body states become delocalized and are able to support weak dc quantum transport similar to transport in glassy systems. As  , the transport becomes classical. The straightforward estimate yields [29]
, the transport becomes classical. The straightforward estimate yields [29]
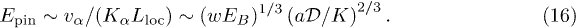
The classical depinning energy is supposed to exceed the quantum energy scale, 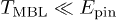 (see footnote 4
). Semiclassical contribution of the composite quasiparticles to the conductivity is estimated as
(see footnote 4
). Semiclassical contribution of the composite quasiparticles to the conductivity is estimated as 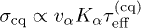 (see footnote 5
), where
(see footnote 5
), where  is a temperature-dependent effective transport time. The value of
is a temperature-dependent effective transport time. The value of  can be estimated as follows: if
can be estimated as follows: if  , semiclassical
, semiclassical  is
is  . This is the scale on which terms
. This is the scale on which terms 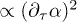 and
and  in
in  , eq. (13), become equal. If
, eq. (13), become equal. If  , the dc conductivity of a disordered Luttinger liquid and, correspondingly,
, the dc conductivity of a disordered Luttinger liquid and, correspondingly,  have the temperature dependence
have the temperature dependence  , see sect. 9.2 in the book [29]. Hence,
, see sect. 9.2 in the book [29]. Hence,  at
at 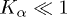 . The temperature must be scaled by Epin to reproduce the value of
. The temperature must be scaled by Epin to reproduce the value of  at
at  . Combining all together and using eq. (14), we find
. Combining all together and using eq. (14), we find 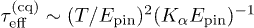 and
and

Equation (17) is valid provided that  . The factor
. The factor  reflects the suppressed Drude weight. Its smallness results in the following important property: the small but finite conductance of the transient samples,
reflects the suppressed Drude weight. Its smallness results in the following important property: the small but finite conductance of the transient samples, 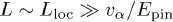 , is almost temperature independent in the interval
, is almost temperature independent in the interval  . To show this, let us estimate the temperature-dependent correction to the conductance governed by the semiclassical conductivity:
. To show this, let us estimate the temperature-dependent correction to the conductance governed by the semiclassical conductivity:  . Using eqs. (15), (16), we obtain
. Using eqs. (15), (16), we obtain  for
for  and
and  . Thus, the temperature-dependent contribution
. Thus, the temperature-dependent contribution  is negligibly small and does not change the total conductance at
is negligibly small and does not change the total conductance at  .
.
Equation (12) is valid at  . Nevertheless, we can draw some qualitative conclusions for
. Nevertheless, we can draw some qualitative conclusions for  , where the dc conductivity is dominated by thermally activated fermions and is estimated as (see footnote 5)
, where the dc conductivity is dominated by thermally activated fermions and is estimated as (see footnote 5)

here 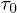 is governed by the disorder of the Kondo lattice, i.e., by the randomness in ρs. The theory for
is governed by the disorder of the Kondo lattice, i.e., by the randomness in ρs. The theory for 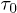 is beyond the scope of the present letter. If
is beyond the scope of the present letter. If  , the gap becomes temperature dependent and shrinks. As a result, our theory looses its validity and the dc transport should reflect different physics.
, the gap becomes temperature dependent and shrinks. As a result, our theory looses its validity and the dc transport should reflect different physics.
Validity
Our consideration is based on several assumptions: The Kondo array is dense, the bare coupling constant is small and the XY-anisotropy is weak,
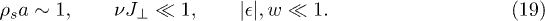
Combining eqs. (2), (19), one can check the inequality  and justify eq. (7).
and justify eq. (7).
We have neglected the Kondo effect which is permissible only provided that Δ exceeds the Kondo temperature of a single Kondo impurity embedded into the HLL, TK. Standard estimates reveal two regimes:  is exponentially small at
is exponentially small at  but becomes larger due to the renormalization of
but becomes larger due to the renormalization of  in the interacting case,
in the interacting case,  at
at 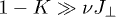 [16]. Comparing TK with Δ from eq. (2), we find that TK is the smallest scale. Thus, for a dense Kondo array, the Kondo screening can be neglected.
[16]. Comparing TK with Δ from eq. (2), we find that TK is the smallest scale. Thus, for a dense Kondo array, the Kondo screening can be neglected.
Taking into account restrictions on K discussed after eq. (12), we determine the condition

which shows that the presented theory is valid in the broad range of interaction strength.
Conclusions and open questions
We have demonstrated that the localization of the 1D helical electrons coupled to the random array of the Kondo impurities is a robust phenomenon which takes place in the broad range of the electron interaction strengths, eq. (20). This confirms a qualitative conjecture of ref. [23]. We have found and quantitatively described strong (non-perturbative) renormalizations of physical parameters, eq. (2).
The second part of the paper addresses possible manifestations of localization in the dc transport at low temperatures T ≪ Δ (Δ is the gap in the electron spectrum caused by local spin ordering). Analysis of this important question may shed light on puzzling experimental results. The current at the low temperature is carried by slow composite spinon-fermion excitations. A random anisotropy of the electron-spin coupling pins spin ordering and localizes low-energy excitations. The localization length  is given by eq. (15). The resulting insulating state persists in a finite temperature interval
is given by eq. (15). The resulting insulating state persists in a finite temperature interval  , where TMBL is the temperature of a many-body localization transition [24]. TMBL is expected to be small compared to the classical depinning energy
, where TMBL is the temperature of a many-body localization transition [24]. TMBL is expected to be small compared to the classical depinning energy 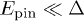 , eq. (16). This physical picture leads to the following predictions: If
, eq. (16). This physical picture leads to the following predictions: If  , the deviation of the conductance from the universal ballistic value should be small as
, the deviation of the conductance from the universal ballistic value should be small as  . Transport in the samples with
. Transport in the samples with  is characterized by the resistive temperature-independent conductance at
is characterized by the resistive temperature-independent conductance at 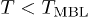 and by temperature-dependent corrections to the conductance which are expected to be much smaller than
and by temperature-dependent corrections to the conductance which are expected to be much smaller than  in the entire interval
in the entire interval 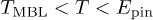 , see analysis after eq. (17). Hence, the conductance of the intermediate samples can remain suppressed and almost temperature independent up to
, see analysis after eq. (17). Hence, the conductance of the intermediate samples can remain suppressed and almost temperature independent up to  . Longer samples,
. Longer samples,  , are almost perfect insulators as long as
, are almost perfect insulators as long as  . More rigorous theory for a temperature interval
. More rigorous theory for a temperature interval  is yet to be developed for both long and short samples. At higher temperatures,
is yet to be developed for both long and short samples. At higher temperatures, 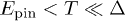 , the dc transport becomes semiclassical with
, the dc transport becomes semiclassical with  , eq. (17), and reduced Drude weight
, eq. (17), and reduced Drude weight  , see eq. (14) (and eq. (3) in ref. [23]).
, see eq. (14) (and eq. (3) in ref. [23]).
To develop the analytical theory, we had to restrict our choice of parameters to those given in eq. (19). In particular, we have assumed a small anisotropy. This choice results in low TMBL and large  . However, a strong XY-anisotropy looks more natural for the edge transport and it could yield stronger localization with larger TMBL and smaller
. However, a strong XY-anisotropy looks more natural for the edge transport and it could yield stronger localization with larger TMBL and smaller 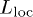 . Therefore, we believe that the considered mechanism of suppressing the ballistic transport can be relevant for realistic samples. In particular, the temperature-independent transport observed in ref. [15] might be associated with the described above resistive regime of relatively short samples at
. Therefore, we believe that the considered mechanism of suppressing the ballistic transport can be relevant for realistic samples. In particular, the temperature-independent transport observed in ref. [15] might be associated with the described above resistive regime of relatively short samples at  . Such a scenario deserves a further study.
. Such a scenario deserves a further study.
Acknowledgments
We gratefully acknowledge hospitality of the Abdus Salam ICTP where the part of this project was done. VIYu also acknowledges the hospitality of the Ludwig Maximilians University, Munich, and the partial support of RFBR grant 15-02-05657. OMYe acknowledges support from the DFG through SFB TR-12, and the Cluster of Excellence, Nanosystems Initiative Munich. We are grateful to I. Aleiner, A. Nersesyan, A. Tsvelik, and I. Yurkevich for useful discussions.
Footnotes
- 1
This hierarchy of energies allows us to neglect the influence of phonons on many-body localization transition: Estimating
 , we conclude that TMBL belongs to the sub-kelvin range where the number of phonons is negligible.
, we conclude that TMBL belongs to the sub-kelvin range where the number of phonons is negligible. - 2
- 3
The equivalence of the fermionic and the bosonic gaps can be seen from the following qualitative reasoning: plasmons are collective excitations above the ground state which is the filled Fermi sea of Dirac fermions. The bosonization procedure requires the normal ordering of the Hamiltonian. Therefore, the free energy of the system must vanish at low temperatures:
 . Technically, it is achieved after subtracting the free energy of the Dirac fermions (the ground-state energy) from the free energy of the bosonized system:
. Technically, it is achieved after subtracting the free energy of the Dirac fermions (the ground-state energy) from the free energy of the bosonized system:  . The path integral formulation governs the simple expression for the partition function of the quadratic bosonic theory
. The path integral formulation governs the simple expression for the partition function of the quadratic bosonic theory ![$Z_{\text{bos}}=\int{\cal D}\{\tilde{\phi}\}\exp(-1/2 [\tilde{\phi}G^{-1}\tilde{\phi}])=\text{det}(G)$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) with the free energy
with the free energy  ; here G is the boson propagator. After inserting the mass term
; here G is the boson propagator. After inserting the mass term  into the Lagrangian
into the Lagrangian  , we obtain the following expression in the frequency-momentum representation:
, we obtain the following expression in the frequency-momentum representation:  . If
. If  , one can easily check that
, one can easily check that  exactly compensates
exactly compensates  at
at  , such that
, such that  . If
. If  ,
,  is changed because of a nonphysical (fake) contribution of the bosons below the gap. This change is cancelled out if the same gap Δ is opened in the spectrum of the Dirac fermions. Thus, the fundamental property
is changed because of a nonphysical (fake) contribution of the bosons below the gap. This change is cancelled out if the same gap Δ is opened in the spectrum of the Dirac fermions. Thus, the fundamental property  requires the equivalence of the bosonic and the fermionic gaps. More details of this thermodynamic consideration will be published elsewhere.
requires the equivalence of the bosonic and the fermionic gaps. More details of this thermodynamic consideration will be published elsewhere. - 4
A rigorous theory for TMBL at
 is missing.
is missing. - 5
The conductivity of a clean Luttinger liquid with the Lagrangian
 reads as
reads as  [29]. The estimate for
[29]. The estimate for  is obtained from
is obtained from  after substituting
after substituting  (respectively, vF) for vK and
(respectively, vF) for vK and for ω at
for ω at  .
.







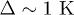


![$Z_{\text{bos}}=\int{\cal D}\{\tilde{\phi}\}\exp(-1/2 [\tilde{\phi}G^{-1}\tilde{\phi}])=\text{det}(G)$](https://content.cld.iop.org/journals/0295-5075/112/5/57003/revision1/epl17568ieqn81.gif)