Abstract
We focus on the damping of the lowest-lying gapped modes with integer angular-momentum quantum number  in carbon nanotubes (CNTs). These modes, called C modes simply, can be predicted within the framework of the continuum elasticity theory with the curvature term. Based on the phonon-phonon interactions due to the anharmonic effect, we obtain the three-phonon coupling coefficients of different damping processes of C modes. Applying perturbation theory, we calculate relaxation rates
in carbon nanotubes (CNTs). These modes, called C modes simply, can be predicted within the framework of the continuum elasticity theory with the curvature term. Based on the phonon-phonon interactions due to the anharmonic effect, we obtain the three-phonon coupling coefficients of different damping processes of C modes. Applying perturbation theory, we calculate relaxation rates  and upper bounds of quality factors for the long-wavelength C modes. In addition, we display the wave vector dependence of
and upper bounds of quality factors for the long-wavelength C modes. In addition, we display the wave vector dependence of  and show the importance of the C mode damping to thermal conductivity.
and show the importance of the C mode damping to thermal conductivity.
Export citation and abstract BibTeX RIS
Introduction
There are several aspects driving the rapidly growing interest into carbon nanotubes (CNTs). On the one hand, their unique properties have been explored frequently in recent years, such as resonant Raman or photoluminescence excitation spectra [1–3], electrical [4], thermal [5–8], and water [9,10] transports, etc. On the other hand, there are also various interesting phenomena observed, such as unusually high-thermal conductivity [11,12], nano-electromechanical effects in suspended CNTs [13–15], and quantum size effects of specific heat [16]. In order to understand such properties and effects, it is crucial to analyze phonon modes and their damping.
Various works have theoretically predicted the phonon spectra through the thin-shell hollow cylinder model [17–21] or the force-constant model [22–24]. In addition, just as usual bulk materials, this kind of quasi–one-dimensional materials can also be considered as continuum elastic medium. Therefore, the phonon modes of CNTs can be well described by the continuum elasticity theory [25–29]. Apart from four acoustic phonon branches (including a longitudinal, a twist, and two degenerate flexural modes), we can also predict two degenerate lowest-lying curvature modes with angular-momentum quantum number  (C modes) via adopting this continuum model with an additional curvature term [18].
(C modes) via adopting this continuum model with an additional curvature term [18].
This work concentrates on the calculation of C mode damping which is quantified by the relaxation rate  , i.e., the inverse relaxation time. The intrinsic damping mechanisms include thermoelastic damping [30–32], phonon-phonon interactions [33–35], defect or impurity scattering [36–39], and electron-phonon interactions [40]. In particular, the damping is mainly caused by phonon-phonon interactions in CNTs, and the important calculations have been presented in refs. [41] and [42]. Moreover, an elegant and persuasive idea indicates that the phonon-phonon interactions can be obtained directly from the continuum elasticity theory mentioned above [43]. Applying this theory with curvature effect, we estimate the quality factor
, i.e., the inverse relaxation time. The intrinsic damping mechanisms include thermoelastic damping [30–32], phonon-phonon interactions [33–35], defect or impurity scattering [36–39], and electron-phonon interactions [40]. In particular, the damping is mainly caused by phonon-phonon interactions in CNTs, and the important calculations have been presented in refs. [41] and [42]. Moreover, an elegant and persuasive idea indicates that the phonon-phonon interactions can be obtained directly from the continuum elasticity theory mentioned above [43]. Applying this theory with curvature effect, we estimate the quality factor 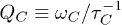 for the C modes with normal frequency
for the C modes with normal frequency  , we show the variation of QC with internal size, and manifest the importance of these relaxation processes to heat conduction. These calculations and analyses have not been done yet in previous works. Recently, some experiments detect the mechanical oscillations excited in suspended CNTs [44,45], and our results will be useful for future experiments.
, we show the variation of QC with internal size, and manifest the importance of these relaxation processes to heat conduction. These calculations and analyses have not been done yet in previous works. Recently, some experiments detect the mechanical oscillations excited in suspended CNTs [44,45], and our results will be useful for future experiments.
Model
To build a coordinate frame, three unit vectors 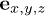 are set as the circumferential, axial and normal directions, respectively, in the cylinder surface of CNTs. The position vector
are set as the circumferential, axial and normal directions, respectively, in the cylinder surface of CNTs. The position vector 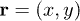 denotes the coordinate of the two-dimensional cylinder surface with two components along
denotes the coordinate of the two-dimensional cylinder surface with two components along 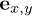 , respectively. To describe the deformation field in the cylinder surface, we also define the displacement vector
, respectively. To describe the deformation field in the cylinder surface, we also define the displacement vector 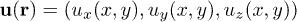 with three components along
with three components along 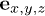 , respectively.
, respectively.
Considering the continuity and isotropy of the surfaces constructing CNTs, the Hamiltonian for decribing the motion of the deformation field can be written as 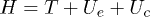 . These three terms denote kinetic energy, elastic energy based on elasticity theory [43], and curvature energy for the phonon branches with
. These three terms denote kinetic energy, elastic energy based on elasticity theory [43], and curvature energy for the phonon branches with  [26], respectively. They are expressed respectively as
[26], respectively. They are expressed respectively as

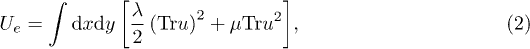

where λ and μ are the Lamé constants (the bulk modulus  ), and the coefficient Ξ describes the surface curvature deviation of CNTs. Their values are
), and the coefficient Ξ describes the surface curvature deviation of CNTs. Their values are  ,
, 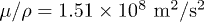 , and
, and 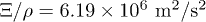 [26,46], in agreement with the empirical force-constant model [47]. In eq. (1),
[26,46], in agreement with the empirical force-constant model [47]. In eq. (1), 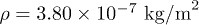 is the mass density of graphenes, and pi is the canonical momentum conjugate to the field variable ui. In eq. (2), according to the elastic model, the strain tensor u consists of linear and nonlinear parts [25], i.e.,
is the mass density of graphenes, and pi is the canonical momentum conjugate to the field variable ui. In eq. (2), according to the elastic model, the strain tensor u consists of linear and nonlinear parts [25], i.e., 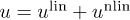 . Its components uij are expressed as
. Its components uij are expressed as

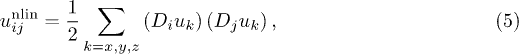
where the covariant derivatives are used for the cylindrical surface structure [25,43]. Furthermore, in eq. (3), R and 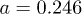 nm denote the tube radius and the ordinary length of a single lattice in CNTs, respectively.
nm denote the tube radius and the ordinary length of a single lattice in CNTs, respectively.
Substituting eqs. (4) and (5) into eq. (2), we obtain the harmonic Hamiltonian as

In addition, the three-phonon coupling Hamiltonian is given by
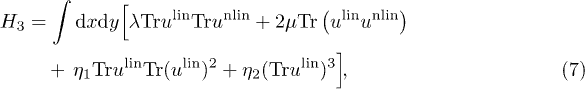
where the first two terms are obtained by substituting eqs. (4) and (5) into eq. (2), and are the coupling terms of linear and nonlinear strain tensors. The higher-order nonlinear terms can also be obtained and involve four-phonon coupling. However, in this paper, these high-order interactions are not considered since the leading processes of the C mode are three-phonon interactions. Besides, a complete cubic-order Hamiltonian should include the additional coupling of three linear parts, namely the last two terms with two new coupling coefficients 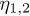 in eq. (7). As shown below, it is the nonlinearity in eq. (2) that dominates in the C mode damping, and
in eq. (7). As shown below, it is the nonlinearity in eq. (2) that dominates in the C mode damping, and 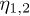 are not required to be estimated for the calculations.
are not required to be estimated for the calculations.
From eq. (6), we can obtain several low-lying modes in the long-wavelength regime. The displacement field 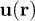 is expressed as Fourier transformation of the momentum representations
is expressed as Fourier transformation of the momentum representations 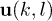 with the wave vector k along
with the wave vector k along 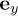 and the angle momentum l along
and the angle momentum l along 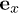 , i.e.,
, i.e., 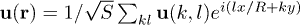 , where
, where 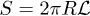 is the cylindrical surface area with tube length
is the cylindrical surface area with tube length  . Inserting it into eq. (6), we can obtain the equation of motion as
. Inserting it into eq. (6), we can obtain the equation of motion as
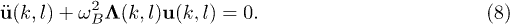
In this equation, 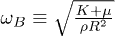 and the matrix
and the matrix  is parameterized with elastic constants as
is parameterized with elastic constants as
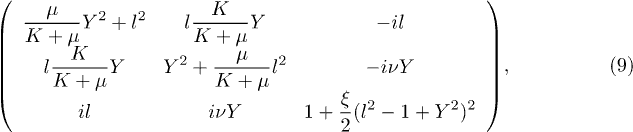
with two dimensionless parameters  and
and 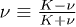 , and a dimensionless variable
, and a dimensionless variable 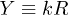 . For a given l, three eigenvalues of
. For a given l, three eigenvalues of 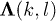 correspond to three normal-mode frequencies
correspond to three normal-mode frequencies 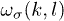 with three polarizations σ, respectively. Each of them corresponds to a specific phonon mode, and is characterized by a unit polarization vector
with three polarizations σ, respectively. Each of them corresponds to a specific phonon mode, and is characterized by a unit polarization vector 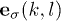 . Obviously,
. Obviously, 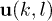 can be expanded a sum running over all polarizations,
can be expanded a sum running over all polarizations,
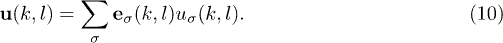
The displacement field is quantized via expressing the normal-mode components 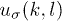 in terms of the boson creation and annihilation operators, namely,
in terms of the boson creation and annihilation operators, namely, 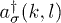 and
and 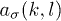 ,
,
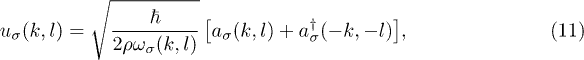
with the communication relation ![$[a_{\sigma}(k,l),a^{\dagger}_{\sigma'}(k',l')]= \delta(k-k') \delta_{\sigma\sigma'}\delta_{ll'}$](https://content.cld.iop.org/journals/0295-5075/113/1/16002/revision1/epl17616ieqn43.gif) . Using this result, the harmonic Hamiltonian (6) is expressed in the quantized form
. Using this result, the harmonic Hamiltonian (6) is expressed in the quantized form
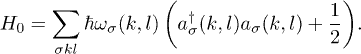
C modes and their couplings
From this model, we obtain the l = 0 modes (including the longitudinal 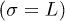 , twist
, twist 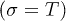 and breathing modes
and breathing modes 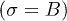 ), the lowest-lying
), the lowest-lying 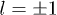 modes
modes 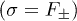 , and the lowest-lying
, and the lowest-lying  modes
modes 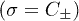 . The general exact results of eq. (9) are complicated. But as for
. The general exact results of eq. (9) are complicated. But as for 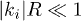 , the high-order terms of kiR are omitted, and the results leave simple forms. Particularly, the C modes are degenerate and their dispersion relation is
, the high-order terms of kiR are omitted, and the results leave simple forms. Particularly, the C modes are degenerate and their dispersion relation is
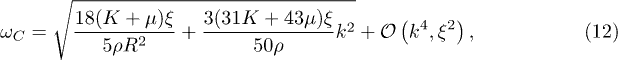
with polarization vector 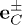 as follows:
as follows:
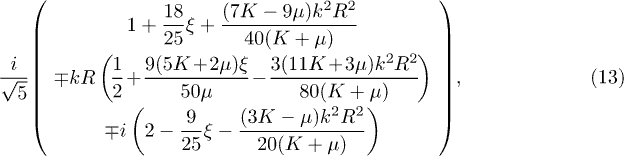
where high-order terms of k and ξ are cut off due to  and the smallness of ξ (about
and the smallness of ξ (about 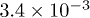 at
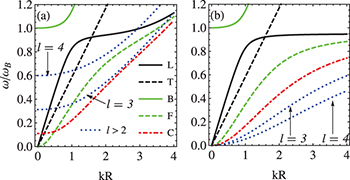
at 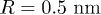 ). Apart from C mode, dispersion relations of other modes can be obtained from this model (see fig. 1), which are similar to the results in ref. [26]. The comparison between (a) and (b) in fig. 1 indicates that the curvature term has an obvious effect on various modes and gives gaps to the l > 1 modes.
). Apart from C mode, dispersion relations of other modes can be obtained from this model (see fig. 1), which are similar to the results in ref. [26]. The comparison between (a) and (b) in fig. 1 indicates that the curvature term has an obvious effect on various modes and gives gaps to the l > 1 modes.
Fig. 1: (Color online) Dispersion relations of a variety of phonon modes for  , including three l = 0 modes and four lowest-lying modes with
, including three l = 0 modes and four lowest-lying modes with 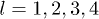 . (a) With curvature term; (b) without curvature term.
. (a) With curvature term; (b) without curvature term.
Download figure:
Standard imageIf expressing eq. (7) in terms of eq. (10), we find that
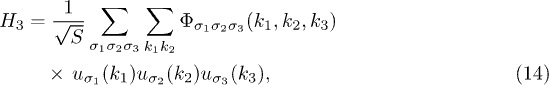
where l is ignored for simplicity, and 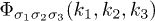 is the three-phonon coupling coefficient. Besides, the summation over wave vectors
is the three-phonon coupling coefficient. Besides, the summation over wave vectors 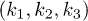 leaves
leaves  on account of momentum conservation
on account of momentum conservation 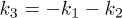 . Due to the degeneration, we only discuss the
. Due to the degeneration, we only discuss the 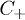 mode damping, and the signs are ignored below. In the long-wavelength regime, both decay
mode damping, and the signs are ignored below. In the long-wavelength regime, both decay 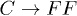 and combination
and combination  allow for the momentum and energy conservations. Since the longitudinal polarization direction (y-component in eq. (13)) of C modes is small, their coupling with longitudinal modes is ignorable. Thus, the process
allow for the momentum and energy conservations. Since the longitudinal polarization direction (y-component in eq. (13)) of C modes is small, their coupling with longitudinal modes is ignorable. Thus, the process 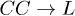 is unimportant. Based on the dispersion relations in
is unimportant. Based on the dispersion relations in 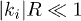 (see fig. 1(a)), the process
(see fig. 1(a)), the process 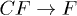 is not allowed, and the frequencies of the l > 2 modes are so high that the C mode cannot merge the
is not allowed, and the frequencies of the l > 2 modes are so high that the C mode cannot merge the 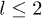 modes into them. Besides, the
modes into them. Besides, the 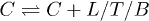 channels are absent because they are kinematically forbidden. In conclusion, the channels
channels are absent because they are kinematically forbidden. In conclusion, the channels 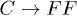 and
and 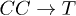 are the dominant damping mechanisms for a long-wavelength C phonon.
are the dominant damping mechanisms for a long-wavelength C phonon.
To derive the coupling coefficient 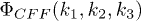 for the decay
for the decay 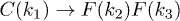 , we obtain the linear part of the strain tensor for C modes via inserting eqs. (10) and (13) into eq. (4),
, we obtain the linear part of the strain tensor for C modes via inserting eqs. (10) and (13) into eq. (4),
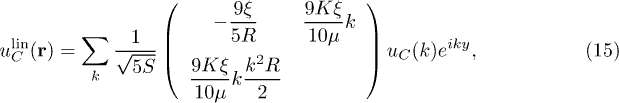
while, by combining eq. (5) with the C mode polarization (13) and the F mode polarization in ref. [43], the nonlinear part mixing C and F modes is
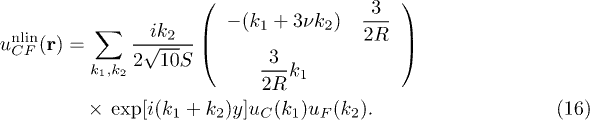
Substituting eqs. (15), (16) and the necessary strain tensors involved F mode in ref. [43] (including the linear part of F mode and the nonlinear part with mixing two F modes) into eq. (7), the leading order of the decay coefficient is obtained via comparing with eq. (14),

In the same way, we obtain the coupling coefficient for the process  :
:
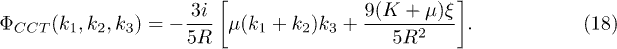
Apart from these linear and nonlinear coupling terms, the additional third-order terms for process 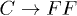 , i.e., the η-coefficient terms in eq. (7), are expressed to leading order as
, i.e., the η-coefficient terms in eq. (7), are expressed to leading order as
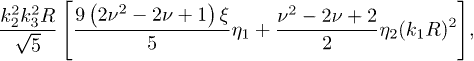
and for the process 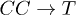 as
as
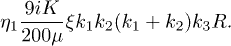
Compared with eqs. (17), (18), both of them are higher order and negligible due to 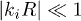 and
and 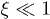 . Therefore, it is unnecessary to estimate
. Therefore, it is unnecessary to estimate 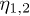 for the calculations.
for the calculations.
Results and discussion
According to Fermi's golden rule [33,48], the single-mode relaxation time for excited phonons with mode K is given by
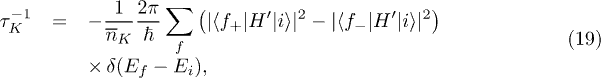
where 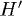 denotes a perturbation Hamiltonian, and
denotes a perturbation Hamiltonian, and  and
and 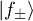 are the initial and final states having NK and
are the initial and final states having NK and 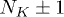 phonons of mode K, respectively. Ei and Ef are the energies of states
phonons of mode K, respectively. Ei and Ef are the energies of states 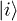 and
and 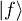 , respectively. Besides,
, respectively. Besides, 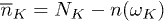 , and
, and ![$n(\Omega)=[\exp{(\hbar \Omega / k_B T)}-1]^{-1}$](https://content.cld.iop.org/journals/0295-5075/113/1/16002/revision1/epl17616ieqn87.gif) is the thermal equilibrium number of phonons with frequency Ω at temperature T. Using the perturbation Hamiltonian (14) in the quantized field form (11), the relaxation rate of the phonon mode (k, σ) that undergoes three-phonon interactions becomes
is the thermal equilibrium number of phonons with frequency Ω at temperature T. Using the perturbation Hamiltonian (14) in the quantized field form (11), the relaxation rate of the phonon mode (k, σ) that undergoes three-phonon interactions becomes
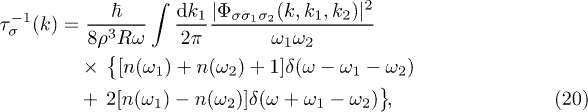
with 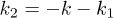 ,
, 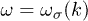 ,
, 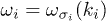 [43]. Its first and second terms indicate the contributions from the decay and merging processes, respectively.
[43]. Its first and second terms indicate the contributions from the decay and merging processes, respectively.
At ultra-low T, only the decay channel 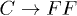 is the leading damping for C modes. Eventually, we obtain this decay rate via eq. (20) with the coupling coefficient (17),
is the leading damping for C modes. Eventually, we obtain this decay rate via eq. (20) with the coupling coefficient (17),
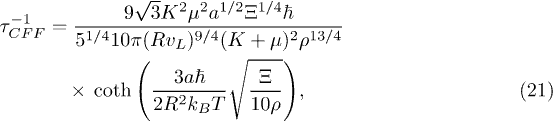
with longitudinal sound velocity 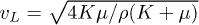 . Keeping the leading order in
. Keeping the leading order in 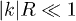 ,
, 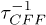 is independent of k, and the quality factor is
is independent of k, and the quality factor is

with the zero-temperature factor
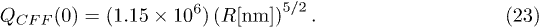
For a typical size  , this yields
, this yields 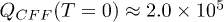 . Taking
. Taking 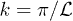 with
with 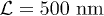 , we display zero-temperature
, we display zero-temperature 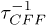 and QCFF vs. the tube radius for the decay
and QCFF vs. the tube radius for the decay 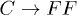 in fig. 2, as well as
in fig. 2, as well as  and QLFF for the decay
and QLFF for the decay 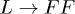 . As shown, the decay effect is easier for thinner CNTs, but the C mode is stronger in thicker CNTs due to the monotonic increase of QCFF. In the range of radii considered, although the C mode decay is easier than the L mode, it is stronger for the C mode than for the L mode under the comparison of their Q-factors.
. As shown, the decay effect is easier for thinner CNTs, but the C mode is stronger in thicker CNTs due to the monotonic increase of QCFF. In the range of radii considered, although the C mode decay is easier than the L mode, it is stronger for the C mode than for the L mode under the comparison of their Q-factors.
Fig. 2: (Color online) The tube radius dependences of the decay rate 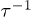 and quality factor Q, which are indicated by left and right vertical axes, respectively, for both processes
and quality factor Q, which are indicated by left and right vertical axes, respectively, for both processes 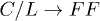 at T = 0 and
at T = 0 and  with
with  .
.
Download figure:
Standard imageAs temperature rises, the merging process 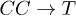 becomes another considerable contribution to the C mode damping. Applying eq. (20) with coupling coefficient (18) instead, we then obtain the relaxation rate as
becomes another considerable contribution to the C mode damping. Applying eq. (20) with coupling coefficient (18) instead, we then obtain the relaxation rate as
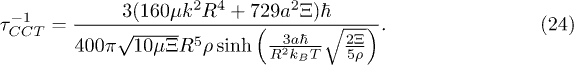
The parameter Ξ in eqs. (21) and (24) manifests that the curvature character of CNTs influences directly the C mode damping. According to dispersion relations without the curvature (see fig. 1(b)), the decay 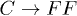 hardly happens since the energy of a C phonon is always lower than that of a F phonon. In contrast, the merging rate of channel
hardly happens since the energy of a C phonon is always lower than that of a F phonon. In contrast, the merging rate of channel 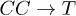 becomes extremely high without considering the curvature (see fig. 3). Hence, it is necessary to take into account the curvature term (3) for our calculation.
becomes extremely high without considering the curvature (see fig. 3). Hence, it is necessary to take into account the curvature term (3) for our calculation.
Fig. 3: (Color online) The damping rate of process  calculated with and without the curvature effect at
calculated with and without the curvature effect at 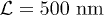 and
and  .
.
Download figure:
Standard imageThe total relaxation rate  for C modes yields
for C modes yields

while the total quality factor is then QC. For 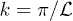 with
with 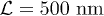 , the R-dependence of the finite-temperature QC is shown in fig. 4. As depicted, this dependence behaviour hardly changes from 0 to 1 K, but the curve becomes flat as T continues rising. Besides, QC of thicker tubes is more sensitive to temperature. Moreover, since QC at 5 K is even larger than the zero-temperature QLFF (see fig. 2), the C mode is stronger than the L mode at
, the R-dependence of the finite-temperature QC is shown in fig. 4. As depicted, this dependence behaviour hardly changes from 0 to 1 K, but the curve becomes flat as T continues rising. Besides, QC of thicker tubes is more sensitive to temperature. Moreover, since QC at 5 K is even larger than the zero-temperature QLFF (see fig. 2), the C mode is stronger than the L mode at 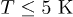 .
.
Fig. 4: (Color online) The tube radius dependence of QC with  at
at 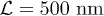 and various temperatures.
and various temperatures.
Download figure:
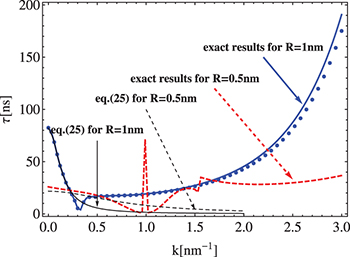
Standard imageTo analyze the wave vector dependence, we adopt the exact 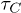 from the exact eigen solutions of eq. (9). At
from the exact eigen solutions of eq. (9). At 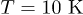 , the
, the 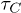 -dependence on the wave vector is displayed in fig. 5, and agrees well with the analytical formula (25) in the low-k regime. Furthermore, we also consider the η-coefficient terms of eq. (7), and find them ignorable even though the
-dependence on the wave vector is displayed in fig. 5, and agrees well with the analytical formula (25) in the low-k regime. Furthermore, we also consider the η-coefficient terms of eq. (7), and find them ignorable even though the 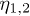 are as large as the elastic parameters in the range of k considered for
are as large as the elastic parameters in the range of k considered for 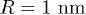 . In other words, the relaxation time is basically determined by parameters K, μ and Ξ at
. In other words, the relaxation time is basically determined by parameters K, μ and Ξ at  in the low-k regime.
in the low-k regime.
Fig. 5: (Color online) The relaxation time 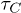 as a function of the wave vector at
as a function of the wave vector at 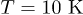 . The thick solid and dotted lines denote the exact
. The thick solid and dotted lines denote the exact  for
for  at
at 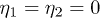 and
and  , respectively. Besides, the results for
, respectively. Besides, the results for  are also shown.
are also shown.
Download figure:
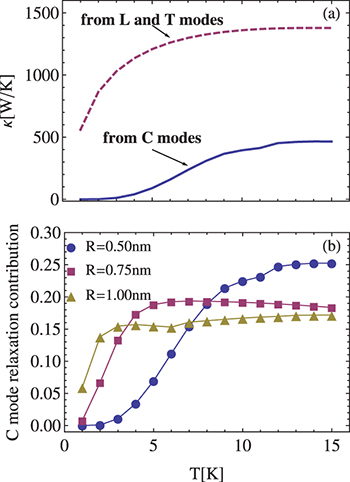
Standard imageThe thermal conductivity κ at given T is expressed as the sum of various phonon modes [49,50], 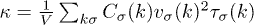 , where V denotes the volume of CNT, and
, where V denotes the volume of CNT, and 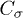 and
and 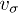 indicate the specific heat and the magnitude of phonon group velocity for specific polarization σ, respectively. On the basis of the k-dependence of the relaxation time
indicate the specific heat and the magnitude of phonon group velocity for specific polarization σ, respectively. On the basis of the k-dependence of the relaxation time 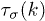 , the T-dependence of thermal conductivity from various polarizations is shown in fig. 6(a) for
, the T-dependence of thermal conductivity from various polarizations is shown in fig. 6(a) for  . Including C modes, the normalized contributions of this gapped-mode relaxation are depicted in fig. 6(b) for various R. At
. Including C modes, the normalized contributions of this gapped-mode relaxation are depicted in fig. 6(b) for various R. At 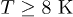 , the relative contributions from the C mode damping tend to increase with R reduction. In the case of
, the relative contributions from the C mode damping tend to increase with R reduction. In the case of 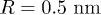 and
and 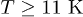 , this contribution rate is up to about 0.25 and therefore, C mode contributions are considerable to the total thermal conductivity in this situation.
, this contribution rate is up to about 0.25 and therefore, C mode contributions are considerable to the total thermal conductivity in this situation.
Fig. 6: (Color online) (a) Thermal conductivity from different polarizations vs. temperature for  ; (b) normalized contributions of C mode relaxation to the total thermal conductivity vs. temperature for
; (b) normalized contributions of C mode relaxation to the total thermal conductivity vs. temperature for 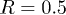 , 0.75, 1 nm.
, 0.75, 1 nm.
Download figure:
Standard imageConclusions
While phonon-phonon scattering rates derived from interatomic potentials are more accurate and reveal the differences for various chiralities [51], the continuum elasticity model provides a simplified and analytical framework to describe reasonably the phonon modes with long wavelength in CNTs [26,52]. Moreover, the latter has been used to predict effectively phonon-phonon scattering rates for modes with  [43,53]. In this paper, we first calculate the relaxation rate
[43,53]. In this paper, we first calculate the relaxation rate 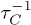 of the lowest-lying
of the lowest-lying 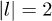 phonons (C modes) based on this model with the curvature-energy term [26].
phonons (C modes) based on this model with the curvature-energy term [26].
The simple and approximate form of 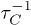 is obtained by only keeping low order of kR terms, and used to calculate the upper bounds for the quality factor QC in the
is obtained by only keeping low order of kR terms, and used to calculate the upper bounds for the quality factor QC in the  regime. Our results suggest that the C mode is stronger than the L mode at
regime. Our results suggest that the C mode is stronger than the L mode at 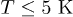 , and QC rises with tube radius increasing at ultra-low temperature. On the other hand, our calculations for thermal conductivity use the exact
, and QC rises with tube radius increasing at ultra-low temperature. On the other hand, our calculations for thermal conductivity use the exact 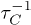 because of involving a relatively large wave vector. As a result, the relative thermal conductivity contributions from the C mode damping are up to 25% at
because of involving a relatively large wave vector. As a result, the relative thermal conductivity contributions from the C mode damping are up to 25% at 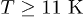 and
and  , which reveals the importance of these contributions to heat conduction in CNTs. We believe that our results are important for predicting the quality factor and thermal conductivity and will be helpful for further experimental and theoretical studies.
, which reveals the importance of these contributions to heat conduction in CNTs. We believe that our results are important for predicting the quality factor and thermal conductivity and will be helpful for further experimental and theoretical studies.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant Nos. 11535004, 11375086, 11120101005, 11175085, and 11235001), by the 973 National Major State Basic Research and Development of China, Grant No. 2013CB834400 and by the Science and Technology Development Fund of Macau under Grant No. 068/2011/A.