Abstract
Two new analytical results are given which are of great help to understand superlattices with coupled modes. The first is an explicit relation for the transfer matrices in terms of Schur functions and Chebyshev polynomials. The second is a condition which generalizes the old well-known Floquet-Bloch trace condition to determine the spectrum. These improvements allow a fast computation of scattering amplitudes without obscuring the calculation with complicated numerical methods. As the energy grows, the eigenvalues degeneracy determines two types of transmission gaps. It is shown that these results could make it possible to design in greater detail the energy spectrum, for the very interesting case including modes coupling and degeneracy. They keep the understanding on the same footing as that of the traditional basic uncoupled problem considered at the beginning of the study of superlattices, like the Kroning-Penning model, or by Floquet-Bloch's theorem, or later by Esaki for heterostructures.
Export citation and abstract BibTeX RIS
Introduction
Since the experimental beginnings of superlattices some decades ago [1], there has been large interest in more complicated devices like those where longitudinal as well as transversal or lateral potentials [2] are designed at will. The confinement at small scales in two directions leads to important effects in the electronic spectra. Translational invariance in both directions is broken, making the physical phenomena richer among other aspects through the coupling of longitudinal normal modes. However, the study of superlattices with two-dimensional potentials has not been conducted with sufficient detail, since advances have been achieved principally for quasi–one-dimensional problems, for which the transversal directions effects have been simplified or uncoupled.
In this letter, superlattices or multilayers with coupled channels are described by sectionally constant potentials in the longitudinal direction and arbitrary lateral dependence, to allow the explicit analytic calculation of the scattering amplitudes. Three characteristic features are considered in detail: number of cells, number of partitions in each cell, and number of coupled normal modes or channels. Using the scattering matrix method, the relevant functions are expressed in terms of Chebyshev polynomials, leading to a transparent analytical and fast numerical tool. It is shown that quantum tunneling and interference phenomena in superlattices with interacting energy modes present features not reported before, along with sharp resonances and threshold effects. In particular, under analytically easily formulated conditions, superlattices with coupled modes lead to either zero transmission for a single mode, or simultaneous exact zero transmission in two or more distinct modes. This behaviour depends on the kind of "colliding" or degenerating eigenvalues, whether they are or not coupled. This last result could make it possible to determine experimentally the coupling strength between modes in a superlattice. The energy spectra are efficiently calculated in a transparent way using simplified symmetric functions.
The (unitary) scattering matrix S is introduced by  , where
, where  and
and  are the incoming and outgoing wave vectors on the left- and right-hand sides of the superlattice. The S-matrix is here given as
are the incoming and outgoing wave vectors on the left- and right-hand sides of the superlattice. The S-matrix is here given as

where the reflection and transmission amplitudes r, t and  , corresponding to the incidence from the left- and right-hand side, respectively, are to be found. The two-terminal conductance [3] is given by Landauer's formula as
, corresponding to the incidence from the left- and right-hand side, respectively, are to be found. The two-terminal conductance [3] is given by Landauer's formula as
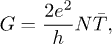
in terms of the average transmission probability  and the number N of transverse channels in the conductor leads.
and the number N of transverse channels in the conductor leads.
For electronic transport in superlattices, formed by sequences of n equal cells and effective mass m, Schrödinger's equation in each cell is given in terms of a two-dimensional external potential  . It is assumed that the superlattice has transversal width w in the y-direction and that electron transport occurs in the longitudinal x-direction. For clarity, the potential is considered as infinite for y outside the interval
. It is assumed that the superlattice has transversal width w in the y-direction and that electron transport occurs in the longitudinal x-direction. For clarity, the potential is considered as infinite for y outside the interval  . It is not possible to uncouple the y-dependence, as is usual in infinite crystals, since there is no translational invariance.
. It is not possible to uncouple the y-dependence, as is usual in infinite crystals, since there is no translational invariance.
Schur functions and the transfer matrix
A direct way to solve the problem is to expand the wave function in N transversal normal modes or channels as  , with
, with  , so that
, so that  . This simple procedure leads to a system of N differential equations
. This simple procedure leads to a system of N differential equations

where  ,
,  , is a symmetric
, is a symmetric  matrix, 1 is the
matrix, 1 is the  identity matrix,
identity matrix,  , and coupling matrix elements
, and coupling matrix elements
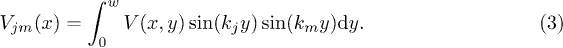
The next step is to divide each cell into a set of I distinct layers with constant matrices  for
for ![$\xi_i\in [x_i,x_{i+1}],\quad i=0,1,\dots,I-1$](https://content.cld.iop.org/journals/0295-5075/114/1/17002/revision1/epl17774ieqn17.gif) . Thus, the longitudinal potential matrix elements are approximated by sectionally constant functions with discontinuities at
. Thus, the longitudinal potential matrix elements are approximated by sectionally constant functions with discontinuities at  for
for  , where x0 and xI denote the boundary points of the cell. Continuity of the wave function and its derivative is imposed at all interfaces between layers.
, where x0 and xI denote the boundary points of the cell. Continuity of the wave function and its derivative is imposed at all interfaces between layers.
Defining  with
with  , it follows that
, it follows that
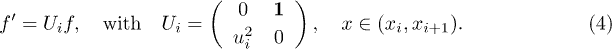
The solution of this system is

with  and where
and where
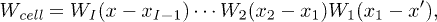
and  . After expanding in power series,
. After expanding in power series,
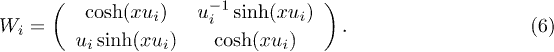
The transfer matrices Wi and  are symplectic. The remaining calculation can be made using the well-known [4] Sylvester formula for matrix functions, which includes the important possibility of degenerated spectra. The transfer matrix W of an arrangement of n adjacent equal cells is the n-th power of the cell matrix
are symplectic. The remaining calculation can be made using the well-known [4] Sylvester formula for matrix functions, which includes the important possibility of degenerated spectra. The transfer matrix W of an arrangement of n adjacent equal cells is the n-th power of the cell matrix  .
.
The application of the Floquet theorem idea [5] to superlattices for eigenvectors leads with eq. (5) to
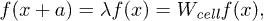
for  , so that the multiplier λ is an eigenvalue of
, so that the multiplier λ is an eigenvalue of  ; i.e., it must satisfy the characteristic equation
; i.e., it must satisfy the characteristic equation

Therefore, to obtain bounded wave vectors  for large superlattices, it is necessary that
for large superlattices, it is necessary that  .
.
The Cayley-Hamilton theorem states that the characteristic polynomial  of
of  is nullified by its eigenvalues as well as by
is nullified by its eigenvalues as well as by  itself. To obtain a relation for the n-th power of
itself. To obtain a relation for the n-th power of  , the usual procedure (see, for example, [6]) is to start with the characteristic equation for
, the usual procedure (see, for example, [6]) is to start with the characteristic equation for  , which leads to the recurrence formula
, which leads to the recurrence formula

with  . Here, em stands for the elementary homogeneous symmetric functions of the eigenvalues
. Here, em stands for the elementary homogeneous symmetric functions of the eigenvalues  . Introducing a generating function, it follows that all powers of
. Introducing a generating function, it follows that all powers of  can be obtained recursively in terms of the first
can be obtained recursively in terms of the first  -th powers of
-th powers of  as
as
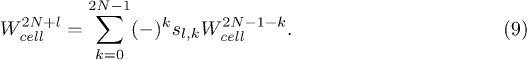
The coefficients sl,k can be explicitly obtained, and are given by the polynomials of degree  ,
,
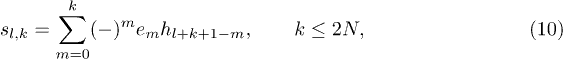
which are the Schur functions [6] for the partition  of the integer
of the integer  as the sum of the integer l + 1 plus k times the unit. The hi are the complete homogeneous symmetric functions of the eigenvalues.
as the sum of the integer l + 1 plus k times the unit. The hi are the complete homogeneous symmetric functions of the eigenvalues.
Having the characteristic polynomial real coefficients, if λ is an eigenvalue, then  is also an eigenvalue, in general distinct. Further, if λ is an eigenvalue, then
is also an eigenvalue, in general distinct. Further, if λ is an eigenvalue, then  is an eigenvalue, too, since the matrix
is an eigenvalue, too, since the matrix  is symplectic,
is symplectic,  and
and  . This leads to the simplification
. This leads to the simplification  , so that only half of the coefficients of the characteristic polynomial need to be computed. Notice that for
, so that only half of the coefficients of the characteristic polynomial need to be computed. Notice that for  , it follows that
, it follows that  and
and  coincide. The polynomial can be written as
coincide. The polynomial can be written as  , where
, where  and a reduced characteristic polynomial
and a reduced characteristic polynomial  , which is a polynomial of N-th degree in μ, halving the computations. The eigenvalues of the reduced characteristic equation,
, which is a polynomial of N-th degree in μ, halving the computations. The eigenvalues of the reduced characteristic equation,  , shall be called here the partial traces, since their sum is the full trace. Introducing
, shall be called here the partial traces, since their sum is the full trace. Introducing  , with
, with  for
for  , the
, the  are complex numbers in general. Considering now the Waring-Louck [7] expression, we have
are complex numbers in general. Considering now the Waring-Louck [7] expression, we have
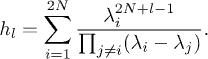
Ordering the eigenvalues as  , hl can be written after some rearrangements as
, hl can be written after some rearrangements as
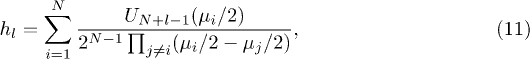
where  is the Chebyshev polynomial of the second kind of the
is the Chebyshev polynomial of the second kind of the  -th degree. The eigenvalues appear only through the partial traces. The functions hl are a kind of Chebyshev polynomials in N variables. This is the generalization of the old result for a single channel leading to the Chebyshev polynomials of the second kind in one variable. Other functions of the eigenvalues can be similarly rewritten. Of importance here is the discriminant of the characteristic polynomial
-th degree. The eigenvalues appear only through the partial traces. The functions hl are a kind of Chebyshev polynomials in N variables. This is the generalization of the old result for a single channel leading to the Chebyshev polynomials of the second kind in one variable. Other functions of the eigenvalues can be similarly rewritten. Of importance here is the discriminant of the characteristic polynomial
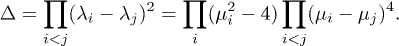
This expression vanishes for degenerated eigenvalues and is of great help to understand the spectrum. From the point of view of the theory of Lie algebras and groups, the important quantity is their rank, which determines how many independent algebra generators are involved.
Energy spectra and Riemann surfaces
The transfer matrix eigenvalues are algebraic functions of the traces of its powers. But since the traces are known analytic functions of the energy, by the implicit function theorem, the energy can be seen as a complex function  of the eigenvalues. Since for sufficiently large energy the Schrödinger equation uncouples, generically, the transfer matrix eigenvalues are asymptotically complex with unit moduli. Topologically, depicted on the surface of a unit cylinder with the energy as axis, the eigenvalues
of the eigenvalues. Since for sufficiently large energy the Schrödinger equation uncouples, generically, the transfer matrix eigenvalues are asymptotically complex with unit moduli. Topologically, depicted on the surface of a unit cylinder with the energy as axis, the eigenvalues  with unit moduli and their inverses will give N pairs of curve segments evolving in opposite senses and intersecting each other at angles 0 and π corresponding to degenerated eigenvalues
with unit moduli and their inverses will give N pairs of curve segments evolving in opposite senses and intersecting each other at angles 0 and π corresponding to degenerated eigenvalues  . For at least two channels, beyond these crossings between inverse eigenvalues, there will also be crossings between curves of distinct eigenvalues,
. For at least two channels, beyond these crossings between inverse eigenvalues, there will also be crossings between curves of distinct eigenvalues,  and
and  for
for  , degenerating at other angles. This is a distinct type of degeneration. For non-zero coupling the curves leave the unit cylinder by increasing or decreasing the radii of the eigenvalues, following some branch of the energy Riemann surface. For zero coupling, after colliding, the eigenvalues remain on the unit cylinder. The eigenvalues collisions can take place in allowed spectral regions, with non-zero transmission, but also in forbiden regions for eigenvalues with non-unit moduli outside or inside the unit cylinder. In the last case, they would not be observed directly.
, degenerating at other angles. This is a distinct type of degeneration. For non-zero coupling the curves leave the unit cylinder by increasing or decreasing the radii of the eigenvalues, following some branch of the energy Riemann surface. For zero coupling, after colliding, the eigenvalues remain on the unit cylinder. The eigenvalues collisions can take place in allowed spectral regions, with non-zero transmission, but also in forbiden regions for eigenvalues with non-unit moduli outside or inside the unit cylinder. In the last case, they would not be observed directly.
The one-channel case
For a periodic lattice and a single channel some of the above facts had been recognized since the times of Bloch, Kronig-Penney and Kramers [8]. For a single channel the reduced characteristic equation is  and leads to the old Kronig-Penney condition
and leads to the old Kronig-Penney condition  for non-zero transmission as used by Esaki [1]. Using
for non-zero transmission as used by Esaki [1]. Using  , the well-known text-book result [9] follows
, the well-known text-book result [9] follows  .
.
Consider now a cell formed by only two layers with potentials V0 and V1, of lengths a and b. To the left in fig. 1 the energy is shown in the vertical direction as a function of λ in the horizontal complex plane for  ,
,  , and
, and  and
and  , as a reference a unit cylinder is also depicted. The two evolving curves correspond to the two roots
, as a reference a unit cylinder is also depicted. The two evolving curves correspond to the two roots  and their projection on the horizontal plane are a unit circle with two small straight real segments, which correspond to the vertical ellipses. To the right, the top figure shows the real part of the complex trace as a function of the eigenvalues, the cubic
and their projection on the horizontal plane are a unit circle with two small straight real segments, which correspond to the vertical ellipses. To the right, the top figure shows the real part of the complex trace as a function of the eigenvalues, the cubic  , for
, for  ,
,  and
and  , intersecting the unit cylinder. The bottom right figure displays a detail with two ellipses joined to two parabolic segments embedded in the Riemann surface. The ellipses correspond to real λ and the parabolic segments to
, intersecting the unit cylinder. The bottom right figure displays a detail with two ellipses joined to two parabolic segments embedded in the Riemann surface. The ellipses correspond to real λ and the parabolic segments to  . The trace of the whole transfer matrix (see blue curve) determines the energy values for which the transmission coefficient is unit, as shown in fig. 2 for 30 layers with
. The trace of the whole transfer matrix (see blue curve) determines the energy values for which the transmission coefficient is unit, as shown in fig. 2 for 30 layers with  ,
,  ,
,  . The eigenvalues are degenerated for
. The eigenvalues are degenerated for  and there is no transmission for those regions for which
and there is no transmission for those regions for which  (see red curve). The figure on the right gives in black the forbidden spectrum for
(see red curve). The figure on the right gives in black the forbidden spectrum for  and energies
and energies  (vertical coordinate).
(vertical coordinate).
Fig. 1: (Colour online) The energy as a function of the eigenvalues for one channel and a detail of its Riemann surface.
Download figure:
Standard imageFig. 2: (Colour online) Left: the one-channel transmission coefficient and absolute value of half the traces. Right: the spectrum.
Download figure:
Standard imageTwo coupled channels
For coupled channels the problem is richer, not only because there are more partial traces, but also due to the presence of sharp resonances and cusps, among other irregularities [10], in the transmission coefficients. The channels will open according to the energy thresholds. Starting below the first energy threshold, the first partial trace to become smaller than two will determine the first branch of the Riemann surface. The subsequent decreasing partial traces will determine the next branches. The diverging Chebyshev polynomials of the traces larger than two are associated to forbidden energy bands. Following the eigenvalues behaviour mentioned above, as the energy increases, all partial traces shall oscillate around the strip ±2 giving rise to N curves with alternating forbidden and allowed energy regions. These curves determine the regions where transmission in a given channel is zero, perfect or only partial. Thus, the new trace conditions are  for non-zero transmission. For
for non-zero transmission. For  , the eigenvalues are degenerated. Further, two or more partial traces could coincide at certain energies, due to degenerated eigenvalues but with
, the eigenvalues are degenerated. Further, two or more partial traces could coincide at certain energies, due to degenerated eigenvalues but with  . Between two consecutive degenerated eigenvalues of this new kind, their moduli would be not equal to one, leading to vanishing transmission coefficients over an energy interval. This fact could be of experimental interest, as far as, for example, the length of the interval would depend on the coupling strength.
. Between two consecutive degenerated eigenvalues of this new kind, their moduli would be not equal to one, leading to vanishing transmission coefficients over an energy interval. This fact could be of experimental interest, as far as, for example, the length of the interval would depend on the coupling strength.
For two channels the reduced equation is  with
with  and
and  . Calling
. Calling  the solutions, the discriminant here is
the solutions, the discriminant here is  and vanishes for degenerated eigenvalues of distinct channels,
and vanishes for degenerated eigenvalues of distinct channels,  , so that
, so that  . When the discriminant is negative, the partial traces shall be complex, so that the transfer matrix eigenvalues will have moduli distinct of unit and, therefore, both transmission coefficents will be zero over the corresponding energy region.
. When the discriminant is negative, the partial traces shall be complex, so that the transfer matrix eigenvalues will have moduli distinct of unit and, therefore, both transmission coefficents will be zero over the corresponding energy region.
The generalized Kronig-Penney condition is  for non-zero transmission and
for non-zero transmission and  for zero transmission for sufficiently large superlattices. Now
for zero transmission for sufficiently large superlattices. Now
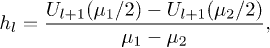
and the generalization of the one-channel formula is
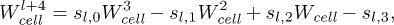
where now  ,
,  ,
,  .
.
As an example consider a superlattice of width w with cells formed by two sections (see fig. 3). The first section has length d1 with a part of width w1 < w at zero potential and a remaining part with a potential barrier of height V0 and width  . The second section has length d2 and zero potential. The potential matrix elements are
. The second section has length d2 and zero potential. The potential matrix elements are  ,
,  ,
, ![$V_{12} = V_0 [\sin(3\pi w_1/w) - 3\sin(\pi w_1/w)]/3\pi$](https://content.cld.iop.org/journals/0295-5075/114/1/17002/revision1/epl17774ieqn108.gif) . There is zero coupling for w1 zero (full wide barrier) or equal to w (no barrier). In fig. 4, to the left, the energy is shown as function of the eigenvalues for
. There is zero coupling for w1 zero (full wide barrier) or equal to w (no barrier). In fig. 4, to the left, the energy is shown as function of the eigenvalues for  ,
,  ,
,  ,
,  and
and  . At the top right the projection of the energy on the eigenvalues plane is given for
. At the top right the projection of the energy on the eigenvalues plane is given for  and 35 Å, respectively. The circles correspond to allowed transmission, whereas the curves outside the unit circles correspond to forbidden regions. The bottom figure to the right shows a section of the Riemann surface containing a joining of surface pieces arising from both eigenvalues.
and 35 Å, respectively. The circles correspond to allowed transmission, whereas the curves outside the unit circles correspond to forbidden regions. The bottom figure to the right shows a section of the Riemann surface containing a joining of surface pieces arising from both eigenvalues.
Fig. 3: (Colour online) A superlattice of total transversal width w and cells with barriers of height V0, width w1 and length d1.
Download figure:
Standard imageFig. 4: (Colour online) The energy for two coupled channels.
Download figure:
Standard imageFigure 5 shows the coefficients T11,  (black continuous and dotted curves) and
(black continuous and dotted curves) and  (thicker curves) for two coupled channels, one-hundred layers with
(thicker curves) for two coupled channels, one-hundred layers with  ,
,  ,
,  ,
,  and
and  . There is no transmission simultaneously for both channels for avoided crossings of the partial traces. In fig. 6 the coefficients T11,
. There is no transmission simultaneously for both channels for avoided crossings of the partial traces. In fig. 6 the coefficients T11,  (black continuous and dotted curves) and
(black continuous and dotted curves) and  (thicker curves) for two coupled channels, are again shown but now, to study the effect of the material parameters on channels coupling, four distinct values of the barriers widths are given: on the top, left, for
(thicker curves) for two coupled channels, are again shown but now, to study the effect of the material parameters on channels coupling, four distinct values of the barriers widths are given: on the top, left, for  ; on the top, right,
; on the top, right,  ; on the bottom, left, for
; on the bottom, left, for  and on the bottom, right, for
and on the bottom, right, for  . A strong dependence on the material parameters is observed and which still needs to be studied thoroughly.
. A strong dependence on the material parameters is observed and which still needs to be studied thoroughly.
Fig. 5: (Colour online) The coefficients T11,  (black continuous and dotted curves) and
(black continuous and dotted curves) and  .
.
Download figure:
Standard imageFig. 6: (Colour online) The coefficients T11,  (black continuous and dotted curves) and
(black continuous and dotted curves) and  , for the same values as in fig. 5, but for
, for the same values as in fig. 5, but for  and 90 Å, from left to right and from top to bottom.
and 90 Å, from left to right and from top to bottom.
Download figure:
Standard imageA more detailed analysis of the spectrum and explicit analytic relations for three and four channels, as well as calculations for superlattices under constant electromagnetic fields, shall be given somewhere else. The obtained results are related to the stability studies of Lyapunov, Krein and others [11]. It seems that similar methods developed for superlattices are also applicable for graphene superlattices [12].











