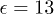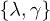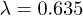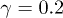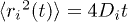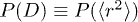Abstract
The dynamical responses of Coulomb-interacting particles in two-dimensional nanoclusters are analyzed at different temperatures characterizing their solid- and liquid-like behavior. Depending on the trap symmetry, spatial correlations undergo slow, stretched exponential relaxations at long times, arising from spatially correlated motion in string-like paths. Such results stem from the combined effects of confinement and long-range repulsion, making the systems inherently heterogeneous. While particles in a "solid" flow produce dynamic heterogeneities, motion in "liquid" yields an unusually long tail in the distribution of particle displacements. A phenomenological model captures much of the subtleties of our numerical simulations.
Export citation and abstract BibTeX RIS
Dynamics of particles in a complex medium is interesting both from fundamental [1,2] and technological [3–5] viewpoints. For example, heterogeneous dynamics [6,7] in glasses show an exponential tail [8] in the distribution of the particle displacements, and belong to the emerging class of "Fickian yet non-Gaussian" motion. A more exotic decay with a "stretched Gaussian" tail (![$\sim \exp\left[-(x/x_0)^{\beta}\right]$](https://content.cld.iop.org/journals/0295-5075/114/4/46001/revision1/epl17843ieqn1.gif) ,
,  ) has been recently found for nanoparticles confined in periodic arrays of nanoposts [2,9]. While the role of hydrodynamic drag [1] and the "core" size of interactions [10] on such slow relaxation are issues of active debate, the local heterogeneity, inherent in many systems, is also a prime suspect. Exploring these inhomogeneities is central to our study.
) has been recently found for nanoparticles confined in periodic arrays of nanoposts [2,9]. While the role of hydrodynamic drag [1] and the "core" size of interactions [10] on such slow relaxation are issues of active debate, the local heterogeneity, inherent in many systems, is also a prime suspect. Exploring these inhomogeneities is central to our study.
One way to induce a heterogeneous response is by confining the system. Motion of trapped particles changes non-trivially not only near the boundary [11], but also deep inside the system, in particular, if the inter-particle interactions are long-ranged. Rich interplay of interactions and the trap geometry on the dynamics of particles at finite temperature  , have been observed in the presence of long-range interactions like for dipolar colloids [12], dusty plasma [13] and Yukawa liquids [14]. With increasing experimental control, clusters of few electrons interacting via Coulomb forces, are fabricated having sizes comparable with the range of interactions [15]. While random impurities describe disorder in bulk systems, a finite system experiences disorder from the irregularities on its "soft" boundary created by electrostatic and magnetic means [16,17]. Such conjecture on the origin of disorder finds support from the measurement of mesoscopic fluctuations [18–20] in chaotic dots. The solid phase of Coulomb clusters at low T is called Wigner Molecule (WM), because it mimics the Wigner crystal [21]. A WM in a circular or irregular trap (defined as CWM and IWM, respectively) melts into a liquid upon increasing temperature [22–25]. The question we ask is: How do a finite number of Coulomb particles reflect the signature of the irregularity in the confining potential and also help in characterizing the thermal melting? Here, we address this question by probing the subtleties of dynamical responses in terms of the Van Hove correlation function (VHCF) [11] for two-dimensional (2D) IWM and CWM, using Molecular-Dynamics (MD) [26] simulations. The VHCF has been routinely used in unfolding the intricacies of spatio-temporal correlations at different length and time scales, yielding crucial information on static and dynamic properties [8,27].
, have been observed in the presence of long-range interactions like for dipolar colloids [12], dusty plasma [13] and Yukawa liquids [14]. With increasing experimental control, clusters of few electrons interacting via Coulomb forces, are fabricated having sizes comparable with the range of interactions [15]. While random impurities describe disorder in bulk systems, a finite system experiences disorder from the irregularities on its "soft" boundary created by electrostatic and magnetic means [16,17]. Such conjecture on the origin of disorder finds support from the measurement of mesoscopic fluctuations [18–20] in chaotic dots. The solid phase of Coulomb clusters at low T is called Wigner Molecule (WM), because it mimics the Wigner crystal [21]. A WM in a circular or irregular trap (defined as CWM and IWM, respectively) melts into a liquid upon increasing temperature [22–25]. The question we ask is: How do a finite number of Coulomb particles reflect the signature of the irregularity in the confining potential and also help in characterizing the thermal melting? Here, we address this question by probing the subtleties of dynamical responses in terms of the Van Hove correlation function (VHCF) [11] for two-dimensional (2D) IWM and CWM, using Molecular-Dynamics (MD) [26] simulations. The VHCF has been routinely used in unfolding the intricacies of spatio-temporal correlations at different length and time scales, yielding crucial information on static and dynamic properties [8,27].
We show that the probability distributions of the displacement of particles, given by the self-part of the VHCF, exhibit a pronounced departure from the standard Gaussian behavior [11]. At low T, this shows a nearly exponential behavior at intermediate times, whereas its long-time profile features multiple peaks. At higher T, the differences between the two traps become more pronounced: While the distribution of the displacement of particles in CWM shows stretched Gaussian relaxation near melting, the IWM shows a stretched exponential trend up to a rather large T. Such distinct dynamical responses are consistent with the mean square displacement of the particles, the spatial displacement pattern and the distinct part of the VHCF. We extend the phenomenological model proposed to explain the non-Gaussian behavior [28] to understand the subtleties of the complex motion in our system.
We model a WM using the Hamiltonian: 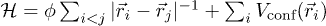 . The first term represents Coulomb repulsion between particles of charge q in the medium with dielectric constant
. The first term represents Coulomb repulsion between particles of charge q in the medium with dielectric constant  , and
, and 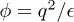 . We consider long-range (unscreened) Coulomb repulsion because the interaction is poorly screened in finite clusters with a small number of particles. Here,
. We consider long-range (unscreened) Coulomb repulsion because the interaction is poorly screened in finite clusters with a small number of particles. Here, 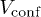 is the confinement potential. We compare results from two traps: a) irregular trap,
is the confinement potential. We compare results from two traps: a) irregular trap, 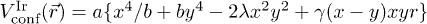 [25,29], and b) circular trap,
[25,29], and b) circular trap,  , where
, where 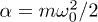 . We rescale the length
. We rescale the length  and energy
and energy 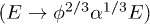 , that transform [22] the CWM Hamiltonian to
, that transform [22] the CWM Hamiltonian to 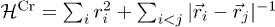 . The time scale is renormalized by
. The time scale is renormalized by  (see footnote 1
). The overall factors a and α are chosen to keep the mean density in the two traps same for a fixed total number of particles, N = 150. Our model of irregular confinement generates dynamics ranging from periodic to chaotic single-particle motion by tuning λ [29]. Such motion along with broken spatial symmetries are taken as footprints of disorder. The irregularity parameters
(see footnote 1
). The overall factors a and α are chosen to keep the mean density in the two traps same for a fixed total number of particles, N = 150. Our model of irregular confinement generates dynamics ranging from periodic to chaotic single-particle motion by tuning λ [29]. Such motion along with broken spatial symmetries are taken as footprints of disorder. The irregularity parameters 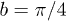 ,
, ![$\lambda \in [0.565, 0.635]$](https://content.cld.iop.org/journals/0295-5075/114/4/46001/revision1/epl17843ieqn19.gif) (which controls chaoticity), and
(which controls chaoticity), and ![$\gamma \in [0.10,0.20]$](https://content.cld.iop.org/journals/0295-5075/114/4/46001/revision1/epl17843ieqn20.gif) (which breaks reflection symmetry) [31] are adjusted to access the standard features of disordered systems [32]. Distances are measured in the unit of r0, the mean inter-particle spacing between neighboring particles at the lowest T. The statistics of results from
(which breaks reflection symmetry) [31] are adjusted to access the standard features of disordered systems [32]. Distances are measured in the unit of r0, the mean inter-particle spacing between neighboring particles at the lowest T. The statistics of results from  are improved by "disorder averaging" [32] over ten configurations, each identified by a specific
are improved by "disorder averaging" [32] over ten configurations, each identified by a specific  . Results from CWM are averaged on ten independent MD simulations.
. Results from CWM are averaged on ten independent MD simulations.
Our calculations are set up in NVT-ensemble using velocity rescaling [26]. The circular confinement conserves the angular momentum to zero (rigid rotation is subtracted from CWM results), and IWM naturally violates it. After equilibration, we study various dynamical quantities, as follows, in order to recognize the intricate response of our system. The density correlation function (obtained from VHCF) [11] is defined as ![$G(r,t)= \langle \sum^{N}_{i,j=1}\delta \left[ r - |\vec{r}_i(t) - \vec{r}_j(0)|\right] \rangle$](https://content.cld.iop.org/journals/0295-5075/114/4/46001/revision1/epl17843ieqn34.gif) , where i and j are particle indices. Here
, where i and j are particle indices. Here 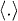 denotes the average over time origins. The self-part
denotes the average over time origins. The self-part  of the VHCF,
of the VHCF, 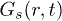 , gives the probability that a particle has traversed a distance r in a time interval t. Its distinct part
, gives the probability that a particle has traversed a distance r in a time interval t. Its distinct part  of VHCF,
of VHCF, 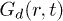 , represents the probability of finding at t a different particle at a distance r from an initial particle. The mean-square displacement (MSD) is defined as
, represents the probability of finding at t a different particle at a distance r from an initial particle. The mean-square displacement (MSD) is defined as ![${\langle \Delta r^2 (t) \rangle = N^{-1} \sum_i \langle\left[ \Delta \vec{r}_i(t) \right]^2\rangle}$](https://content.cld.iop.org/journals/0295-5075/114/4/46001/revision1/epl17843ieqn40.gif) , where
, where 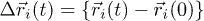 .
.
A thermal crossover from a "solid" to "liquid" in WM asserts [22,25] a "solid" at  and "liquid" at
and "liquid" at 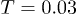 for the chosen parameters. Here we consider the temperature range
for the chosen parameters. Here we consider the temperature range 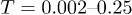 which encompasses the equilibrium crossover. In order to study the spatio-temporal correlations in our system, we first investigate the time dependence of
which encompasses the equilibrium crossover. In order to study the spatio-temporal correlations in our system, we first investigate the time dependence of 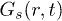 [27], represented in a semi-logarithmic plot in fig. 1. Thus, at any given time t, a Gaussian r-dependence of
[27], represented in a semi-logarithmic plot in fig. 1. Thus, at any given time t, a Gaussian r-dependence of 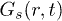 appears as an inverted parabola in this plot. Depicting the low
appears as an inverted parabola in this plot. Depicting the low 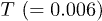 results of
results of 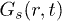 , fig. 1(a) illustrates that the dynamics in IWM can be broadly classified into three temporal regimes2
: i) Ballistic motion occurs for short time
, fig. 1(a) illustrates that the dynamics in IWM can be broadly classified into three temporal regimes2
: i) Ballistic motion occurs for short time 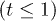 yielding Gaussian
yielding Gaussian  . Particles feel each other's presence only for t > 1 implying that our unit time represents the time scale of interaction. ii) Particles get "arrested" in the cage formed by neighbors during the intermediate times
. Particles feel each other's presence only for t > 1 implying that our unit time represents the time scale of interaction. ii) Particles get "arrested" in the cage formed by neighbors during the intermediate times 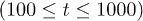 , reflected in the bunched up traces of
, reflected in the bunched up traces of 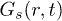 in the inset of fig. 1(a). iii) The dynamics for large time
in the inset of fig. 1(a). iii) The dynamics for large time 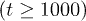 develops multiple peaks in
develops multiple peaks in  . The motion in the CWM (fig. 1(b)) is broadly similar to IWM insofar as the temporal regimes are concerned, albeit the caging regime is narrow
. The motion in the CWM (fig. 1(b)) is broadly similar to IWM insofar as the temporal regimes are concerned, albeit the caging regime is narrow 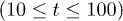 and untenable, causing weaker agglomeration of
and untenable, causing weaker agglomeration of 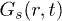 (inset, fig. 1(b)).
(inset, fig. 1(b)).
Fig. 1: (Color online) Upper panels: the spatial decay of 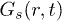 (normalized by
(normalized by 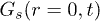 ), in a semi-logarithmic plot, for several t in the "solid"
), in a semi-logarithmic plot, for several t in the "solid" 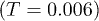 : (a) IWM, (b) CWM.
: (a) IWM, (b) CWM. 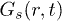 is Gaussian up to
is Gaussian up to  and displays different non-Gaussian trends for
and displays different non-Gaussian trends for  , including multi-peak structures for
, including multi-peak structures for  . The traces of
. The traces of  for
for 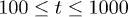 bunch up (weaker in CWM) as shown in the insets demonstrating caging. Lower panels: the decay of
bunch up (weaker in CWM) as shown in the insets demonstrating caging. Lower panels: the decay of  in the "liquid"
in the "liquid" 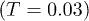 also shows deviations from the Gaussian behavior (except for small t): (c) IWM, (d) CWM.
also shows deviations from the Gaussian behavior (except for small t): (c) IWM, (d) CWM.
Download figure:
Standard imageFig. 2: (Color online) The nature of the spatial evolution of 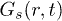 for CWM and IWM is analyzed in (a) and (b), respectively, by studying the exponents
for CWM and IWM is analyzed in (a) and (b), respectively, by studying the exponents 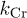 and
and 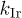 (see text). A continuous decay of
(see text). A continuous decay of 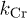 and
and 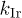 from 2 to nearly 1 occurs at the lowest T (insets (a2) and (b1)). The circular trap yields
from 2 to nearly 1 occurs at the lowest T (insets (a2) and (b1)). The circular trap yields 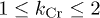 for all T, whereas
for all T, whereas 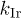 degrades to values smaller than unity. Inset (a1) of panel (a): illustration of the fitting of
degrades to values smaller than unity. Inset (a1) of panel (a): illustration of the fitting of  curve with two functional dependences:
curve with two functional dependences: 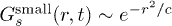 for
for 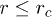 , and
, and 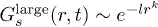 for r > rc. rc denotes the optimal distance for which the total
for r > rc. rc denotes the optimal distance for which the total 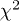 is minimum.
is minimum.
Download figure:
Standard imageAt high temperatures, in a normal liquid, particles undergo diffusive motion resulting in a Gaussian  . We find that for both
. We find that for both 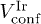 and
and 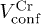 ,
, 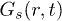 deviates from Gaussian even beyond the thermal crossover point
deviates from Gaussian even beyond the thermal crossover point 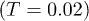 . The deviation is more pronounced in
. The deviation is more pronounced in 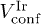 , where it undergoes a progressively slower decline. Such differences in the behavior of
, where it undergoes a progressively slower decline. Such differences in the behavior of 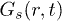 persist in the two confinements (fig. 1(c), (d)) at temperatures beyond "melting".
persist in the two confinements (fig. 1(c), (d)) at temperatures beyond "melting".
Next, we quantify the r-dependence of 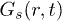 , for a given t, by fitting it to two functional dependences:
, for a given t, by fitting it to two functional dependences: 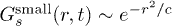 for
for 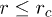 , and
, and 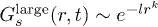 for r > rc. This is implemented in the parameter sub-space of
for r > rc. This is implemented in the parameter sub-space of  , in which the r-dependence of
, in which the r-dependence of 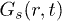 has a monotonic evolution (this turns out to be
has a monotonic evolution (this turns out to be 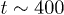 for
for 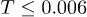 and the entire t range for T > 0.006). For each region (r smaller or larger than rc), our fitting procedure yields a value for
and the entire t range for T > 0.006). For each region (r smaller or larger than rc), our fitting procedure yields a value for 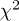 , measuring the goodness of the fit in that region. The final accepted value of rc is the one that minimizes the total
, measuring the goodness of the fit in that region. The final accepted value of rc is the one that minimizes the total 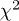 of the fit on the entire r-axis. The same prescription also obtains the other optimal fit parameters, e.g., c, l, k, etc. The inset (a1) of fig. 2(a) illustrates the procedure described above.
of the fit on the entire r-axis. The same prescription also obtains the other optimal fit parameters, e.g., c, l, k, etc. The inset (a1) of fig. 2(a) illustrates the procedure described above.
Figure 2((a) CWM; (b) IWM) presents the time evolution of the parameter k that quantifies the nature of the decay of  . Gaussian behavior corresponds to k = 2. Henceforth, we denote the corresponding k for irregular and circular traps as
. Gaussian behavior corresponds to k = 2. Henceforth, we denote the corresponding k for irregular and circular traps as 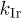 and
and 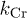 , respectively. For low
, respectively. For low 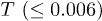 , both
, both  and
and 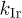 degrade close to unity (insets (a2) and (b1)) establishing a near-exponential decay [8] in the "solid" for large times. With increasing T, the long-time limit of
degrade close to unity (insets (a2) and (b1)) establishing a near-exponential decay [8] in the "solid" for large times. With increasing T, the long-time limit of 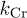 rises; however, it broadly remains within
rises; however, it broadly remains within 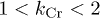 (main panel of fig. 2(a)) confirming a stretched Gaussian trend, as observed in recent experiments [2,9]. In striking contrast,
(main panel of fig. 2(a)) confirming a stretched Gaussian trend, as observed in recent experiments [2,9]. In striking contrast,  decreases with t causing a stretched exponential (i.e.,
decreases with t causing a stretched exponential (i.e., 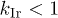 ) spatial decay (fig. 2(b)). Interestingly,
) spatial decay (fig. 2(b)). Interestingly,  reaches its minimum for
reaches its minimum for 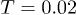 , a temperature that marks the crossover between "solid" and "liquid" [25,33]. Beyond this crossover temperature, the traces of
, a temperature that marks the crossover between "solid" and "liquid" [25,33]. Beyond this crossover temperature, the traces of 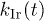 start rising after an initial decrease up to
start rising after an initial decrease up to 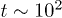 . The irregular system begins to resemble a conventional liquid (i.e.,
. The irregular system begins to resemble a conventional liquid (i.e., 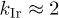 for large t) only for
for large t) only for 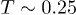 . In contrast, the circular confinement yields
. In contrast, the circular confinement yields  at large t for
at large t for 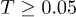 only. We emphasize that our result of k = 2 implies that the whole
only. We emphasize that our result of k = 2 implies that the whole 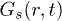 curve has a single Gaussian fall. Thus, the nature of VHCF identifies and distinguishes a solid-liquid crossover in different trap geometries. While a multiple-Gaussian [34] fall (all centred at r = 0) with different widths in different ranges of r can also have k = 2, our results do not correspond to such behavior.
curve has a single Gaussian fall. Thus, the nature of VHCF identifies and distinguishes a solid-liquid crossover in different trap geometries. While a multiple-Gaussian [34] fall (all centred at r = 0) with different widths in different ranges of r can also have k = 2, our results do not correspond to such behavior.
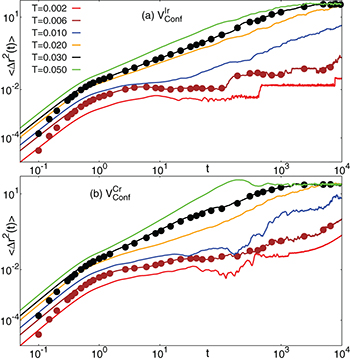
The classification of temporal regimes at low T is also realized in MSD  as shown in fig. 3((a) IWM; (b) CWM) in a double-logarithmic plot. At all temperatures, for both the confinements, we see for
as shown in fig. 3((a) IWM; (b) CWM) in a double-logarithmic plot. At all temperatures, for both the confinements, we see for 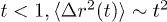 . Thus, it represents the ballistic regime. After this initial temporal regime, the low-T evolution of MSD is surprisingly flat for IWM from strong caging, whereas, CWM shows a weak Brownian behavior. Such a wide plateau in MSD (spread over several decades) for an IWM, as well as its occasional jumps, are reminiscent of glassy dynamics [35]. The plateau at intermediate t shrinks gradually with T causing a smooth crossover between ballistic and Fickian motion. The "jumps" also fade away with T. In contrast, neither a clear plateau, nor such jumps are discernible in CWM even at low T. At long time, MSD saturates when displacements approach the system size. MSD is also estimated from the VHCF as
. Thus, it represents the ballistic regime. After this initial temporal regime, the low-T evolution of MSD is surprisingly flat for IWM from strong caging, whereas, CWM shows a weak Brownian behavior. Such a wide plateau in MSD (spread over several decades) for an IWM, as well as its occasional jumps, are reminiscent of glassy dynamics [35]. The plateau at intermediate t shrinks gradually with T causing a smooth crossover between ballistic and Fickian motion. The "jumps" also fade away with T. In contrast, neither a clear plateau, nor such jumps are discernible in CWM even at low T. At long time, MSD saturates when displacements approach the system size. MSD is also estimated from the VHCF as 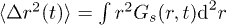 , and its evaluation is shown as dots in fig. 3(a), (b), confirming the Fickian regime for
, and its evaluation is shown as dots in fig. 3(a), (b), confirming the Fickian regime for 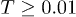 . Interestingly, these regimes are rife with non-Gaussian motion, cf. fig. 3(a), (b). Thus, our results corroborate the notion of "Fickian yet non-Gaussian" dynamics [1,36] at long times. Overall signatures of MSD indicate that IWM resembles a supercooled system [35] more than CWM does.
. Interestingly, these regimes are rife with non-Gaussian motion, cf. fig. 3(a), (b). Thus, our results corroborate the notion of "Fickian yet non-Gaussian" dynamics [1,36] at long times. Overall signatures of MSD indicate that IWM resembles a supercooled system [35] more than CWM does.
Fig. 3: (Color online) The time dependence of the mean-square displacement (MSD) at different temperatures is shown for (a) irregular and (b) circular traps. The dots represent MSD by integrating 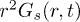 (see text), and are shown only for
(see text), and are shown only for 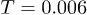 and 0.03. The near-perfect match between the solid traces and corresponding dots, however, persists for all T.
and 0.03. The near-perfect match between the solid traces and corresponding dots, however, persists for all T.
Download figure:
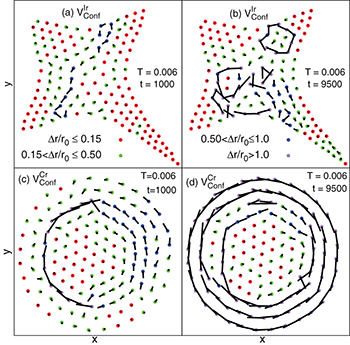
Standard imageDoes the spatial reorganization of the moving particles gel with the above unfolding of  ? In order to develop a deeper understanding, we analyze the particle displacements,
? In order to develop a deeper understanding, we analyze the particle displacements, 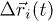 in fig. 4. In the figure, thick dots represent the initial position of the particles and the connecting line signifies the displacement of the same particle at the specified time t. Different colors represent particles with different ranges of magnitude of the displacement,
in fig. 4. In the figure, thick dots represent the initial position of the particles and the connecting line signifies the displacement of the same particle at the specified time t. Different colors represent particles with different ranges of magnitude of the displacement, 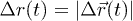 . In fig. 4, we see that most particles only rattle around their equilibrium positions for
. In fig. 4, we see that most particles only rattle around their equilibrium positions for  . Motion that begins by breaking a cage causes avalanches of such events correlated in space, leading to a string-like path of delocalization [37,38]. Avalanche of such cage breaking events, whenever occurring, sets up in a very short time interval. Figure 4(a) presents
. Motion that begins by breaking a cage causes avalanches of such events correlated in space, leading to a string-like path of delocalization [37,38]. Avalanche of such cage breaking events, whenever occurring, sets up in a very short time interval. Figure 4(a) presents 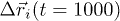 for an IWM at
for an IWM at 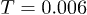 , showing string-like alignment of neighboring particles yielding a slow relaxation producing a long tail in
, showing string-like alignment of neighboring particles yielding a slow relaxation producing a long tail in 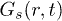 . Once the collective motion subsumes most of the system, particles undergo relatively small displacements, but an overall drift, producing secondary peaks. With further increase in t, the string-like path degenerates into sub-clusters, each performing independent collective motion (fig. 4(b)), and contribute to the multi-peak
. Once the collective motion subsumes most of the system, particles undergo relatively small displacements, but an overall drift, producing secondary peaks. With further increase in t, the string-like path degenerates into sub-clusters, each performing independent collective motion (fig. 4(b)), and contribute to the multi-peak  of fig. 1.
of fig. 1.
Fig. 4: (Color online) Displacement  plots for
plots for  are shown ((a), (b): IWM; (c) (d): CWM) for t = 1000 and t = 9500, illustrating the motional coherence. The thick dots represent the initial position and the connecting lines signify the displacements of the same particle at t. Red, green, blue, and purple dots represent particles with increasing
are shown ((a), (b): IWM; (c) (d): CWM) for t = 1000 and t = 9500, illustrating the motional coherence. The thick dots represent the initial position and the connecting lines signify the displacements of the same particle at t. Red, green, blue, and purple dots represent particles with increasing  . The mobile particles reside in the central region for
. The mobile particles reside in the central region for  , leaving the nearly immobile ones in the narrow limbs near corners. In contrast, the mobile particles in CWM circle around the periphery, while the slow ones flock towards the origin.
, leaving the nearly immobile ones in the narrow limbs near corners. In contrast, the mobile particles in CWM circle around the periphery, while the slow ones flock towards the origin.
Download figure:
Standard imageThe differences between the two traps stand out in the nature of motional coherence. The strings at low T in a CWM (fig. 4(c), (d)) become approximately circular respecting azimuthal symmetry. This symmetry is well maintained at intermediate and long times, particularly near the boundary. Intriguingly, the mobile particles travel by several "lattice spacings" riding on the coherence even in the "solid" phase3! Signatures of such spatially correlated motion of particles, have been realized in thermal melting of circular plasma crystals [13], and also in a flocking transition of driven granular classical matter in confinements [39].
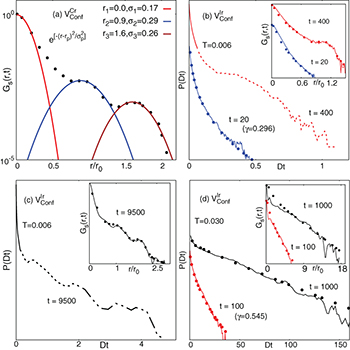
A phenomenological proposition to access the non-Gaussian behavior of 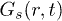 is to express it as a convolution of Gaussian particle displacements and their distribution of diffusivities P(D) [28,40]. We generalize this idea to accommodate its multi-peak nature at low T and large t:
is to express it as a convolution of Gaussian particle displacements and their distribution of diffusivities P(D) [28,40]. We generalize this idea to accommodate its multi-peak nature at low T and large t:
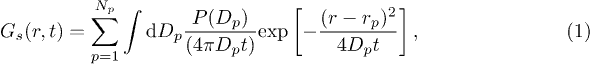
assuming  has Np peaks. Naturally, a monotonic decay results for p = 1. A departure from the Gaussian behavior is thus crucially attributed by P(D) which is now a superposition of the individual distributions
has Np peaks. Naturally, a monotonic decay results for p = 1. A departure from the Gaussian behavior is thus crucially attributed by P(D) which is now a superposition of the individual distributions 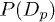 for each p. We access
for each p. We access 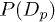 by first obtaining rp and the corresponding peak width by fitting the individual peaks of
by first obtaining rp and the corresponding peak width by fitting the individual peaks of 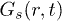 (fig. 5(a)). We then determine
(fig. 5(a)). We then determine  from the statistics of individual particles whose
from the statistics of individual particles whose 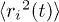 lies within the peak width at a given rp (see footnote 4). The resulting P(D) shows a long tail indicating striking inhomogeneities at all different temperatures. Such broad distribution is a footprint of dynamic heterogeneity [35], i.e., multiple time scale relaxations in a single system. P(D) shows exponential, and stretched exponential tails for up to intermediate times at low
lies within the peak width at a given rp (see footnote 4). The resulting P(D) shows a long tail indicating striking inhomogeneities at all different temperatures. Such broad distribution is a footprint of dynamic heterogeneity [35], i.e., multiple time scale relaxations in a single system. P(D) shows exponential, and stretched exponential tails for up to intermediate times at low 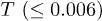 and becomes unusually broad with near-flat sections at large t. The long tail (mostly stretched exponential) in P(D) persists even at high
and becomes unusually broad with near-flat sections at large t. The long tail (mostly stretched exponential) in P(D) persists even at high 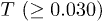 . The different nature of P(D) in separate ranges of D at long t and low T, is consistent with the physical picture presented in fig. 3. Interestingly, the
. The different nature of P(D) in separate ranges of D at long t and low T, is consistent with the physical picture presented in fig. 3. Interestingly, the 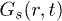 obtained from eq. (1) using the aforementioned extraction of P(D) matches almost perfectly (insets of fig. 5(b)–(d)) with direct simulations. While in fig. 5(b)–(d) data are shown only for irregular confinement, a broad matching holds even for circular confinement.
obtained from eq. (1) using the aforementioned extraction of P(D) matches almost perfectly (insets of fig. 5(b)–(d)) with direct simulations. While in fig. 5(b)–(d) data are shown only for irregular confinement, a broad matching holds even for circular confinement.
Fig. 5: (Color online) Panel (a) shows the Gaussian fit of all three peaks of a representative 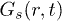 . The distributions of diffusivity, P(D), are shown for irregular confinements (b)–(d), in a semi-logarithmic plot. This distribution with monotonic D-dependence often satisfies
. The distributions of diffusivity, P(D), are shown for irregular confinements (b)–(d), in a semi-logarithmic plot. This distribution with monotonic D-dependence often satisfies 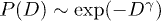 , and the corresponding γ's are shown in parentheses (panels (b), (d)). Panel (c) shows P(D) for
, and the corresponding γ's are shown in parentheses (panels (b), (d)). Panel (c) shows P(D) for 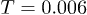 at t = 9500 (yielding multi-peak
at t = 9500 (yielding multi-peak 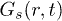 ). It shows rich structures beyond a sharp initial fall. The insets show favourable comparison of
). It shows rich structures beyond a sharp initial fall. The insets show favourable comparison of 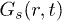 obtained from MD simulations (solid lines) with its evaluation using eq. (1), represented by thick dots. The rich structure of P(D) and its long tail indicate profound heterogeneous diffusion.
obtained from MD simulations (solid lines) with its evaluation using eq. (1), represented by thick dots. The rich structure of P(D) and its long tail indicate profound heterogeneous diffusion.
Download figure:
Standard imageThe multiple relaxations are also probed by 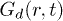 , the distinct part of VHCF. In the small-time limit
, the distinct part of VHCF. In the small-time limit 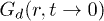 represents pair correlation function, g(r) [11,25], and thus consists of sharp peaks, like crystals, at low T. Figure 6(a) shows depleted peaks of
represents pair correlation function, g(r) [11,25], and thus consists of sharp peaks, like crystals, at low T. Figure 6(a) shows depleted peaks of 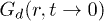 for IWM indicating a lack of positional order even at low
for IWM indicating a lack of positional order even at low 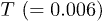 [25], while a CWM displays sharper peaks (fig. 6(b)) due to the azimuthal ordering in the symmetry direction. It is interesting to note the distinct role of the "fast" and "slow" particles towards the time evolution of
[25], while a CWM displays sharper peaks (fig. 6(b)) due to the azimuthal ordering in the symmetry direction. It is interesting to note the distinct role of the "fast" and "slow" particles towards the time evolution of 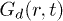 . A particle is qualified as "fast" ("slow") if its mobility lies within the top (bottom) 7% (10%) – the mobility of the i-th particle being defined as
. A particle is qualified as "fast" ("slow") if its mobility lies within the top (bottom) 7% (10%) – the mobility of the i-th particle being defined as 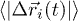 . The long-time accumulation of
. The long-time accumulation of 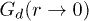 (fig. 6(a), (b)) arises from the fast particles occupying the locations from where another particle moved out – thereby developing the spatially correlated motion. In contrast, the slow particles trace out the sharp peaks of
(fig. 6(a), (b)) arises from the fast particles occupying the locations from where another particle moved out – thereby developing the spatially correlated motion. In contrast, the slow particles trace out the sharp peaks of  . The inset of fig. 6(b) illustrates such distinct behavior for
. The inset of fig. 6(b) illustrates such distinct behavior for  . A similar picture emerges from the self-part, too – while the slow particles produce the small-r (Gaussian) behavior, the fast particles contribute to the long tail, see the inset of fig. 5(a). Figure 6(c), (d) shows
. A similar picture emerges from the self-part, too – while the slow particles produce the small-r (Gaussian) behavior, the fast particles contribute to the long tail, see the inset of fig. 5(a). Figure 6(c), (d) shows 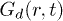 at
at 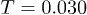 for the IWM and CWM, respectively. As expected in a liquid, the large-r peaks are already washed out at smallest t. Its relaxation with time smoothens out even the weak modulations leaving only the strong peak at r = 0. The long-time filling of the gap at
for the IWM and CWM, respectively. As expected in a liquid, the large-r peaks are already washed out at smallest t. Its relaxation with time smoothens out even the weak modulations leaving only the strong peak at r = 0. The long-time filling of the gap at 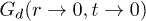 seems stronger in the irregular trap than in circular confinement at
seems stronger in the irregular trap than in circular confinement at 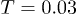 , unlike for low
, unlike for low 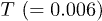 where such filling is similar, irrespectively of the geometry. This is indicative of the fact that the spatially correlated motion causing such filling has more pronounced effects on the irregular trap, which, in turn, leads to ultra-slow relaxation in them.
where such filling is similar, irrespectively of the geometry. This is indicative of the fact that the spatially correlated motion causing such filling has more pronounced effects on the irregular trap, which, in turn, leads to ultra-slow relaxation in them.
Fig. 6: (Color online) Distinct part of VHCF, 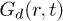 , for several t in the "solid", depicting the temporal relaxation in (a) IWM and (b) CWM. The "correlation hole" in
, for several t in the "solid", depicting the temporal relaxation in (a) IWM and (b) CWM. The "correlation hole" in 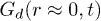 fills up with time producing a peak at large t. The inset of (a) identifies the contribution of slow (brown) and fast (blue) particles in
fills up with time producing a peak at large t. The inset of (a) identifies the contribution of slow (brown) and fast (blue) particles in  . The fast particles contribute to
. The fast particles contribute to 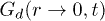 , while the slow ones trace the frozen "solid" (inset (b)). Panels (c) and (d) show
, while the slow ones trace the frozen "solid" (inset (b)). Panels (c) and (d) show 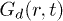 with r for several t in the "liquid" for IWM and CWM, respectively. The "correlation hole" in
with r for several t in the "liquid" for IWM and CWM, respectively. The "correlation hole" in  fills up very quickly for both confinements in the high-T phase.
fills up very quickly for both confinements in the high-T phase.
Download figure:
Standard imageIn conclusion, we show that the interplay of interactions and trap geometry leads to dynamic heterogeneity, producing unconventional dynamical behavior, like an ultra-slow spatial relaxation in Wigner molecules. We ensure that our qualitative results survive for  , and we expect these to persist for other disordered traps [15]. VHCF and its variants are directly probed in experiments [34]. While the exponential tail in
, and we expect these to persist for other disordered traps [15]. VHCF and its variants are directly probed in experiments [34]. While the exponential tail in 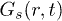 is common in experiments and simulations on colloids [36], gels [34], glasses [7,8,41,42], and bio-molecule suspensions [43], our finding of its stretched exponential decay opens a new direction, to the best of our knowledge. Our results will motivate further experiments probing the role of local heterogeneity on complex motion providing guidance in designing nanotechnology devices exploiting the geometry of the confinement.
is common in experiments and simulations on colloids [36], gels [34], glasses [7,8,41,42], and bio-molecule suspensions [43], our finding of its stretched exponential decay opens a new direction, to the best of our knowledge. Our results will motivate further experiments probing the role of local heterogeneity on complex motion providing guidance in designing nanotechnology devices exploiting the geometry of the confinement.
Acknowledgments
We thank Deepak Dhar and Chandan Dasgupta for valuable discussions. BA acknowledges his doctoral fellowship from the University Grant Commission (UGC), India.
Footnotes
- 1
Our scaled energy and time unit take the values 1.7 meV and 376 fs, for electrons in circular quantum dot using bare parameters for GaAs heterostructures (
 ,
,  , the mass of an electron,
, the mass of an electron,  ,
,  ) [30].
) [30]. - 2
- 3
The coalescing azimuthal motion in the CWM at large t is different from a rigid rotation, which is easily tracked in the periodic modulation of the mean-square displacement, and subtracted from all our results.
- 4
We obtain P(D) using MSD,
 for all particles i. Also
for all particles i. Also  for a fixed t and the equivalence was used for convenience.
for a fixed t and the equivalence was used for convenience.