Abstract
We consider a theoretical model describing the "anomalous heating" of charged grains due to their stochastic motion in the volume of a spatially inhomogeneous plasma. On the basis of this model for the first time we propose the analytical relations for conditions of the heating of grains due to the gradient of their charge in the electric field of a trap. The obtained relations were tested by numerical simulations of the problem for one and two charged particles.
Export citation and abstract BibTeX RIS
Studies of mechanisms of the energy exchange in systems of interacting particles are of significant interest in various areas of science and engineering (plasma physics, medicine, biology, polymer physics, etc.) [1–8]. A dusty plasma is an ionized gas containing charged grains (dust) of micron sizes. This plasma is widespread in nature and is produced in a number of technological processes [1–3]. The majority of laboratory studies of dusty plasma is carried out in gas discharges of various types [9–13].
In a weakly ionized plasma the massive dust particles efficiently dissipate their kinetic energy through collisions with gas neutrals (atoms/molecules). It is often assumed that as a result of the energy exchange between the dust and neutral components, they are in equilibrium. Nevertheless, experiments show that the stochastic kinetic energy of dust in a laboratory plasma can be considerably higher than the temperature of surrounding gas, 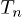 , and can reach the values
, and can reach the values  . This phenomenon is usually called "anomalous heating". The mechanisms of this "heating" are commonly associated with various temporal and spatial fluctuations of dust charges [14–19]. However, the existing theoretical models do not always allow one to explain the gain of high kinetic energies for typical experimental conditions [20–23].
. This phenomenon is usually called "anomalous heating". The mechanisms of this "heating" are commonly associated with various temporal and spatial fluctuations of dust charges [14–19]. However, the existing theoretical models do not always allow one to explain the gain of high kinetic energies for typical experimental conditions [20–23].
The charge of a dust particle is not a fixed quantity, it is determined by the local plasma parameters near this particle (for example, by the electron and/or ion number densities and their velocities) [1,2]. Two main factors that can lead to random dust charge fluctuations, that, in turn, can be the reason for the formation of irregular stochastic motion of dust, exist. The first of them is associated with the random nature of the ion/electron currents charging the dust particles [14,15]. The second is determined by the stochastic motion of dust in the volume of a spatially inhomogeneous plasma [24–26].
Since the dust charge is a function of the surrounding plasma parameters, a change in these parameters can lead to changes in the grain charge and the development of various instabilities in the dusty plasma [16–18,26–28]. The formation of regular self-oscillations (large-scale rotations and oscillations of separate particles) in the field of nonelectrostatic forces orthogonal to the grain charge gradient was considered in [16–18]. Besides the development of regular self-oscillations, in the numerical simulations of the problem the "anomalous heating" of the particles (the nature of which has had till now no satisfactory explanation) was also observed. Notice that all types of grain motions mentioned above are observed in laboratory experiments with gas-discharge plasma [17,18,26–30].
Stochastic fluctuations in the dust charge, which are determined by the random motion of grains in a spatially inhomogeneous plasma (due to their thermal or other types of fluctuations) in the presence of a dust charge gradient in the direction of the gravity force, are one of the possible mechanisms for the development of irregular oscillations of grains [26,28]. However, the first of the proposed models [26] describes the mechanism for the excitation of dust oscillations due to the collective fluctuations of interparticle forces in the dust cloud; the second model [28] is based on the assumption of free dust diffusion that is unsuitable for limited (finite) trajectories of dust particles often observed in laboratory plasma [1–3]. Thus, the above-mentioned models do not allow to describe the "heating" of an isolated dust particle due to its charge gradient in the field of a trap.
In this paper we present the mechanism describing the "anomalous heating" of charged grains due to their stochastic motion in the volume of a spatially inhomogeneous plasma. The proposed theoretical model was considered for one and two particles with the gradient of their charge for typical conditions of laboratory experiments in gas-discharge plasma. Analysis of such small-sized systems admits a simple analytical solution of the problem and provides a qualitative picture of the energy exchange in extended systems.
Let us consider the system of two linearized equations of motion that describe the displacements (ξ1 and ξ2) of one or two interacting identical particles with mass M from their equilibrium positions in the field of external forces under the action of a random force  ,
,


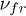 is the friction coefficient of the grains due to their collisions with gas neutrals, and the coefficients
is the friction coefficient of the grains due to their collisions with gas neutrals, and the coefficients 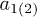 ,
, 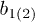 depend on the physics of a solved problem. In this case, the correlators of force
depend on the physics of a solved problem. In this case, the correlators of force  obey the equations:
obey the equations: 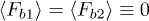 ,
,  ,
, 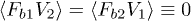 ,
, 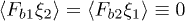 ,
,  ,
,  , where
, where 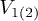 are the velocities per degree of freedom. Hereinafter the brackets
are the velocities per degree of freedom. Hereinafter the brackets 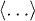 denote the time averaging (for
denote the time averaging (for 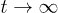 ).
).The various classes of physical problems (such as the problem of stable positions of one or two particles in the external electric field [31–34], and some problems of stable positions of charged particles in an extended dust cloud [16–18]) can be described by equations similar to eqs. (1a), (1b).
A solution of eqs. (1a), (1b) is always unstable for 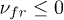 or
or 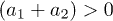 [24]. Let us investigate the stability of solutions for the system (1a), (1b) with arbitrary coefficients
[24]. Let us investigate the stability of solutions for the system (1a), (1b) with arbitrary coefficients 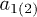 and
and 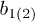 for
for 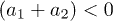 and
and 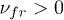 in two cases: i) when
in two cases: i) when ![$s = [(a_{1}-a_{2})^{2}/4 + b_{1}b_{2}]^{1/2}$](https://content.cld.iop.org/journals/0295-5075/115/1/10007/revision1/epl17987ieqn25.gif) is real, and ii) when s is imaginary. In the first case i), the condition for the development of a dissipative instability [7] in the system (1a), (1b) can be represented as
is real, and ii) when s is imaginary. In the first case i), the condition for the development of a dissipative instability [7] in the system (1a), (1b) can be represented as

In the ii) case, the criterion for the development of a dispersive instability [7] in the system can be written as
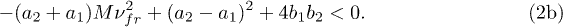
Let us consider the conditions when the energy of the chaotic motion of grains (their kinetic temperature) 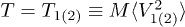 can be above their predetermined temperature
can be above their predetermined temperature 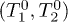 , i.e., the possibility of a gain of additional energy
, i.e., the possibility of a gain of additional energy 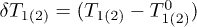 by the dust particles due to the forces acting in the system. Distinction of kinetic temperatures
by the dust particles due to the forces acting in the system. Distinction of kinetic temperatures 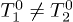 for different degrees of freedom or for different particles can be caused by various mechanisms of the gain of kinetic energy for dust in plasma (for example, fluctuations of dust charges caused by discrete currents of charging [24]). In the absence of sources of additional energy the value of
for different degrees of freedom or for different particles can be caused by various mechanisms of the gain of kinetic energy for dust in plasma (for example, fluctuations of dust charges caused by discrete currents of charging [24]). In the absence of sources of additional energy the value of 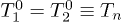 .
.
In the case of finite trajectories: 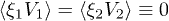 ,
, 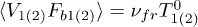 , and we can write the equations for the correlators of grain velocities and displacements
, and we can write the equations for the correlators of grain velocities and displacements



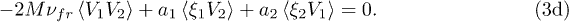
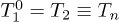 , the solution of eqs. (3a)–(3d) is the relation describing the gain of additional energy
, the solution of eqs. (3a)–(3d) is the relation describing the gain of additional energy 
which is similar to the relation proposed for the case of nonreciprocal interaction of two particles [24,25] and/or for the case of a single grain with charge gradient [24] in a linear electric field. The energy redistribution (between degrees of freedom or between two different grains) in the system being studied can be easily found by taking into account that:  . Notice that in the case of
. Notice that in the case of 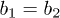 :
: 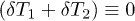 . In systems with the significant dissipation (for
. In systems with the significant dissipation (for  ), the increment in kinetic energy
), the increment in kinetic energy  0, while the ratio
0, while the ratio 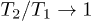 .
.
Thus, the gain of additional energy 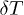 is determined by the stochastic motion of dust in the volume of a spatially inhomogeneous plasma. Since the work of the forces along a closed loop in such systems is
is determined by the stochastic motion of dust in the volume of a spatially inhomogeneous plasma. Since the work of the forces along a closed loop in such systems is 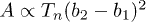 , the additional increment in kinetic energy is
, the additional increment in kinetic energy is 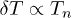 .
.
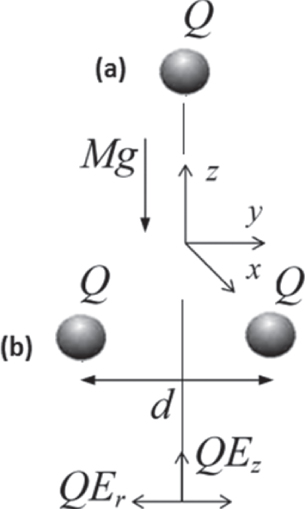
Below we will consider the solution of a problem for one and two identical particles with charge 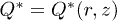 in the field of gravity Mg compensated by the electric field
in the field of gravity Mg compensated by the electric field 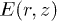 of cylindrical trap with radial component
of cylindrical trap with radial component 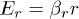 and vertical component
and vertical component 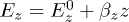 , see fig. 1. Here
, see fig. 1. Here 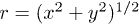 is the radial coordinate, z is the coordinate along an axis parallel to gravity,
is the radial coordinate, z is the coordinate along an axis parallel to gravity, 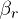 and
and 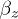 are the values of gradients of electric field, and
are the values of gradients of electric field, and 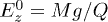 is defined by balance of the forces acting in the system; here Q is the charge in a balance point.
is defined by balance of the forces acting in the system; here Q is the charge in a balance point.
Fig. 1: Positions of one (a) and two (b) charged grains in the electric field of a cylindrically symmetric trap.
Download figure:
Standard imageFig. 2: The ratio of 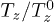 vs.
vs. 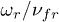 in the one-particle systems with
in the one-particle systems with 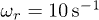 ,
,  for
for  and: (1; ) αr/Q = 0.05 cm−1,
and: (1; ) αr/Q = 0.05 cm−1, 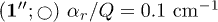 ; for
; for 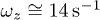 and: (2; ) αr/Q = 0.05 cm−1,
and: (2; ) αr/Q = 0.05 cm−1,  ; for
; for 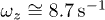 and: (3; ) αr/Q = 0.05 cm−1,
and: (3; ) αr/Q = 0.05 cm−1,  . Continuous lines are the analytical curves. Symbols are the results of numerical simulations.
. Continuous lines are the analytical curves. Symbols are the results of numerical simulations.
Download figure:
Standard imageThe system of motion equations for one particle with charge 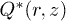 and its gradient
and its gradient 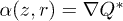 in the linear electric field
in the linear electric field 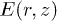 can be written in the form (1a), (1b) where the values of
can be written in the form (1a), (1b) where the values of 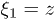 ,
, 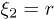 , and z, r are the displacements of the particle from its equilibrium position,
, and z, r are the displacements of the particle from its equilibrium position, 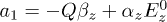 ,
, 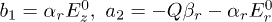 ,
, 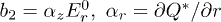 ,
, 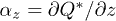 ,
, 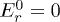 and
and 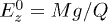 . In this case the value of
. In this case the value of 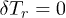 , and the solution of (1a), (1b) that describes the gain of additional energy can be presented as
, and the solution of (1a), (1b) that describes the gain of additional energy can be presented as

Dependences of 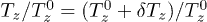 on the ratio of
on the ratio of 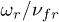 for one charged grain in the systems with
for one charged grain in the systems with  ,
, 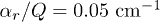 and
and 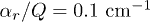 for various parameters of electric trap
for various parameters of electric trap 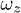 are shown in fig. 2; here
are shown in fig. 2; here 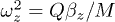 ,
, 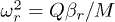 . Detailed study of an influence of plasma densities on the gradients of grain charges was presented in ref. [18] where it has been shown that in the laboratory plasma of capacitive RF discharges the value of the relative gradients of dust charges can reach
. Detailed study of an influence of plasma densities on the gradients of grain charges was presented in ref. [18] where it has been shown that in the laboratory plasma of capacitive RF discharges the value of the relative gradients of dust charges can reach 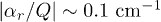 ,
, 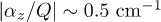 .
.
It is easy to see (fig. 2), that the gain of additional energy by the grains due to the gradients of their charges is comparable in magnitude to the dust heating caused by discrete currents of charging [14,15,24,35]. Because the latter mechanism (associated with the random nature of the ion/electron currents charging of dust is inherent for all types of plasma, it can be assumed that the efficiency of the anomalous heating of grains due to the dust charge gradients may turn out to be considerably higher because the gain of additional energy (5) will be defined by the value of 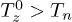 .
.
Here we note that for the case 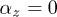 with
with 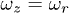 the energy
the energy 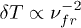 (5), and it can be assumed that
(5), and it can be assumed that  can increase indefinitely with the friction forces decrease (for
can increase indefinitely with the friction forces decrease (for 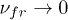 ). However, in real physical systems (such as, for example, a dusty plasma), a dynamic equilibrium is often established between the incoming and scattering energies. The increase in the kinetic energy of particles in such systems can be restricted owing to the existence of certain boundary conditions or peculiarities of the spatial distribution of parameters of the medium, which ensure a progressive growth of the dissipative losses, and due to various dispersion effects, which phenomenologically play a dissipative role [7,16]. In addition, various nonlinear effects can manifest themselves during the anomalous heating of particles [7,16–18,34].
). However, in real physical systems (such as, for example, a dusty plasma), a dynamic equilibrium is often established between the incoming and scattering energies. The increase in the kinetic energy of particles in such systems can be restricted owing to the existence of certain boundary conditions or peculiarities of the spatial distribution of parameters of the medium, which ensure a progressive growth of the dissipative losses, and due to various dispersion effects, which phenomenologically play a dissipative role [7,16]. In addition, various nonlinear effects can manifest themselves during the anomalous heating of particles [7,16–18,34].
We consider the system of two identical particles located at a distance d that are interacting with the force 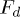 , see fig. 1(b). For this case the motion equations may be presented as
, see fig. 1(b). For this case the motion equations may be presented as
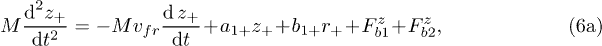


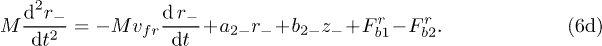
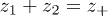 ;
;  ;
; 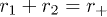 ;
;  (where
(where 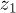 ,
, 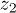 ,
, 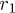 ,
,  are the displacements of particles 1 and 2 from their equilibrium positions) and
are the displacements of particles 1 and 2 from their equilibrium positions) and  ,
, 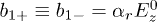 ,
, 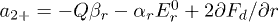 ,
, 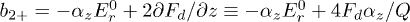 ,
, 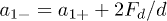 ,
, 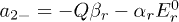 ,
,  , where
, where 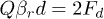 ,
, 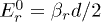 and
and  .
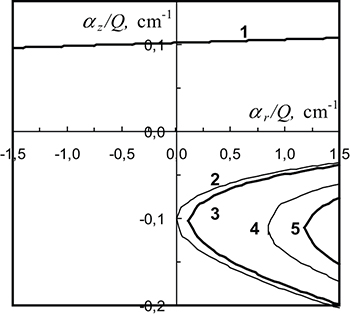
.Fig. 3: Illustration of the regions of steady solutions of the problem for two grains vs.  and
and 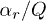 for
for 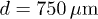 ,
,  and
and 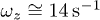 . The region of formation of dissipative instability (7b) is located above the curve 1). Regions of dispersive instability (7c) are bounded by the curves 2)–5) (an internal area) for various
. The region of formation of dissipative instability (7b) is located above the curve 1). Regions of dispersive instability (7c) are bounded by the curves 2)–5) (an internal area) for various 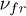 :
: 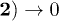 ;
;  ;
; 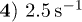 ;
; 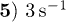 .
.
Download figure:
Standard imageThe conditions of instabilities for a solution of (6a)–(6d) with 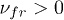 and
and 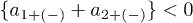 can be represented as
can be represented as


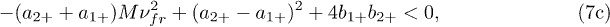

Regions of the steady solutions of a problem for two grains with Coulomb interaction 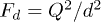 ,
, 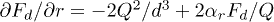 depending on the gradients of their charge, including the lines of development of dissipative (7b) and dispersive (7c) instabilities, are shown in a fig. 3 for the systems with parameters
depending on the gradients of their charge, including the lines of development of dissipative (7b) and dispersive (7c) instabilities, are shown in a fig. 3 for the systems with parameters 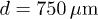 ,
, 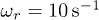 and
and  . In the systems without the gradients of charges (at
. In the systems without the gradients of charges (at  ), the conditions (7a), (7b) completely correspond to the criteria of infringement of stability of a horizontal configuration of two particles interacting with various types of potentials [31–34].
), the conditions (7a), (7b) completely correspond to the criteria of infringement of stability of a horizontal configuration of two particles interacting with various types of potentials [31–34].
For two identical grains: 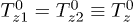 ,
, 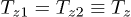 ,
, 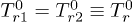 and
and 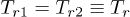 . Then, in case of
. Then, in case of 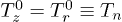 , the solution of (6a)–(6d) can be written as
, the solution of (6a)–(6d) can be written as
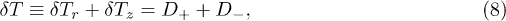
where
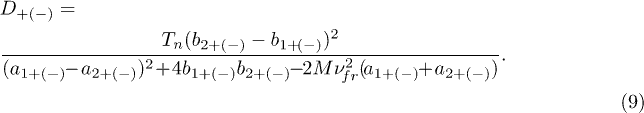
For the correlation functions of the velocities 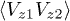 and
and 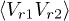 , where
, where 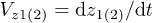 ,
, 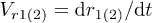 , we obtain
, we obtain





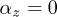 the value of
the value of 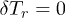 ,
, 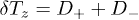 , and for
, and for 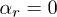 :
:  ,
, 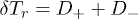 .
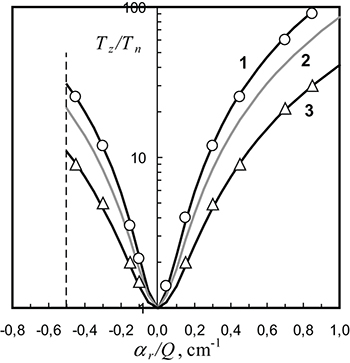
.Fig. 4: The ratio of 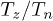 vs.
vs. 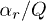 for the two-particle systems with
for the two-particle systems with 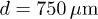 ,
,  ,
, 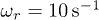 , and
, and 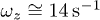 for various
for various 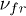 :
: 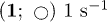 ;
; 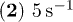 ;
; 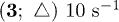 . Continuous lines correspond to analytical curves (12b). Symbols are the results of numerical simulations. The line of formation of dissipative instability is designated by the dashed curve.
. Continuous lines correspond to analytical curves (12b). Symbols are the results of numerical simulations. The line of formation of dissipative instability is designated by the dashed curve.
Download figure:
Standard imageFig. 5: The ratio of  vs.
vs. 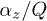 for the two-particle systems with
for the two-particle systems with 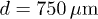 ,
, 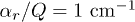 ,
, 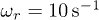 , and
, and  for various
for various  :
: 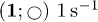 ; (2;
; (2;  )
)  . Continuous lines are the analytical curves (12b). Symbols are the results of numerical simulations. The lines of formation of dispersive instability are designated by the dashed curves.
. Continuous lines are the analytical curves (12b). Symbols are the results of numerical simulations. The lines of formation of dispersive instability are designated by the dashed curves.
Download figure:
Standard imageNotice that in most cases 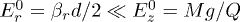 , and, accordingly, for comparable values of
, and, accordingly, for comparable values of 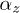 and
and 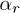 the magnitude
the magnitude 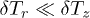 . Dependences of
. Dependences of 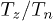 on
on 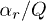 for various parameters of the system are shown in fig. 4, and the dependence of
for various parameters of the system are shown in fig. 4, and the dependence of 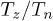 on
on 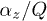 is presented in fig. 5.
is presented in fig. 5.
The dynamics of one 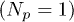 and two
and two 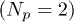 grains with charge
grains with charge 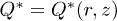 in the field of gravity
in the field of gravity 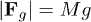 balanced by the electric field E of the cylindrical trap with components
balanced by the electric field E of the cylindrical trap with components 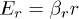 and
and 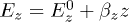 (see figs. 1(a), (b)) was studied by the Langevin molecular dynamic method. This method is based on the solution of the system of
(see figs. 1(a), (b)) was studied by the Langevin molecular dynamic method. This method is based on the solution of the system of  differential equations of motions with random force
differential equations of motions with random force 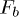 which is a source of stochastic ("thermal") motions of particles with the kinetic temperature
which is a source of stochastic ("thermal") motions of particles with the kinetic temperature 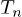 [1,2]. In our case the equations of motions can be presented as
[1,2]. In our case the equations of motions can be presented as
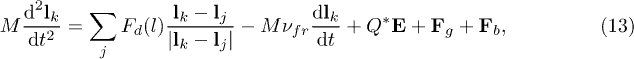
where 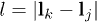 is the inter-grain distance,
is the inter-grain distance, 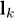 is the vector of position of the mass centre for the k-grain, and
is the vector of position of the mass centre for the k-grain, and 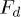 is the force of interaction between two particles
is the force of interaction between two particles 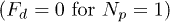 .
.
The analytical model described above is valid for pair interactions of various types. Here for an examination of this model the simulations of the systems consisting of two particles were carried out for Coulomb pair interaction, 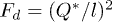 . Notice that the Coulomb asymptotes
. Notice that the Coulomb asymptotes 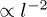 for inter-grain interactions were observed in a laboratory RF discharge plasma [36].
for inter-grain interactions were observed in a laboratory RF discharge plasma [36].
The time integration step 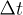 for solution of eq. (13) was from
for solution of eq. (13) was from 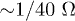 to
to 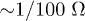 where
where 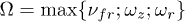 [1,2]. The temperature of grains was set as
[1,2]. The temperature of grains was set as 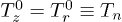 , where the magnitude of
, where the magnitude of  was changed from
was changed from 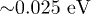 to
to 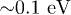 . Relative values of charge gradients
. Relative values of charge gradients 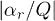 and
and  were varied from 0 to
were varied from 0 to 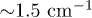 . The magnitude of the vertical electric field of the trap
. The magnitude of the vertical electric field of the trap 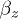 was from
was from 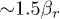 to
to 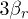 , that provided the steady existence of a horizontal configuration for the two particles (
, that provided the steady existence of a horizontal configuration for the two particles (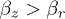 [31–34]). The characteristic frequency of the trap
[31–34]). The characteristic frequency of the trap  was changed from
was changed from 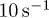 to
to  . The value of the scaling parameter
. The value of the scaling parameter  was from
was from 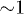 to
to 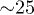 , that is typical for the conditions of laboratory experiments in a gas discharge plasma [1–3].
, that is typical for the conditions of laboratory experiments in a gas discharge plasma [1–3].
Under conditions corresponding to the steady solution of a problem an additional kinetic energy 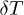 was registered in the simulated systems. In all cases the observed distributions of grain velocities were close to Maxwellian functions, with
was registered in the simulated systems. In all cases the observed distributions of grain velocities were close to Maxwellian functions, with  , and
, and 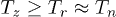 . The value of additional energy was proportional to the originally predetermined temperature of particles,
. The value of additional energy was proportional to the originally predetermined temperature of particles,  . Thus, the "anomalous heating" systems which was accompanied by a nonuniform distribution of energy on the degrees of freedom was observed. Under a steady condition of the simulated system an additional kinetic energy
. Thus, the "anomalous heating" systems which was accompanied by a nonuniform distribution of energy on the degrees of freedom was observed. Under a steady condition of the simulated system an additional kinetic energy 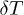 was registered. In all cases the observed distributions of grain velocities were close to Maxwellian functions, with
was registered. In all cases the observed distributions of grain velocities were close to Maxwellian functions, with  , and
, and 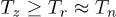 . The value of the additional energy was proportional to the predetermined temperature of particles,
. The value of the additional energy was proportional to the predetermined temperature of particles,  . Thus, the "anomalous heating" systems which was accompanied by a nonuniform distribution of energy on the degrees of freedom was observed.
. Thus, the "anomalous heating" systems which was accompanied by a nonuniform distribution of energy on the degrees of freedom was observed.
The results of numerical simulations for the case of one particle are presented in fig. 2 together with analytical solutions of this problem. Comparison of the results of numerical simulations with theoretical curves for two-particle systems is shown in figs. 4, 5. It is easy to notice the good accordance of numerical data with the proposed analytical relations. Deviations between the theoretical and numerical data were less 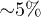 (up to a point of formation of instabilities in the two particle-systems). In the case of development of dispersive instability the motion of grains represented their synchronous regular oscillations which are considerably different from stochastic fluctuations. And in the case of development of dissipative instability we observed the change of horizontal configuration in the arrangement of particles on their vertical orientation.
(up to a point of formation of instabilities in the two particle-systems). In the case of development of dispersive instability the motion of grains represented their synchronous regular oscillations which are considerably different from stochastic fluctuations. And in the case of development of dissipative instability we observed the change of horizontal configuration in the arrangement of particles on their vertical orientation.
In conclusion, we underline that in this paper we present the results of numerical and theoretical investigations of the dynamics of grains with charge gradients in external electric fields. The mechanism describing the "anomalous heating" of charged grains due to their stochastic motion in the volume of a spatially inhomogeneous plasma was considered, and new analytical relations for conditions of the grain heating were proposed. It has been shown that the presented mechanism is an effective source of additional stochastic energy for charged dust particles in laboratory plasmas along with alternative mechanisms such as the discrete currents of charging and/or the nonreciprocal interactions (caused by ion flows), that were proposed earlier for an explanation of the nature of "anomalous heating" of grains [14,15,24,25]. The estimation of the influence of the presented mechanism on the behavior of grains in plasma can be obtained for concrete conditions (with additional estimations of gradients of dust charges [18]) on the basis of proposed relations.
The results of the presented study can be useful for analyzing the energy exchange in inhomogeneous systems, which are of interest in plasma physics, medicine, biology, and the physics of polymers and colloidal systems.
Acknowledgments
We acknowledge financial support by the Russian Foundation for Basic Research (Grants Nos. 16-08-00594, 15-32-21159).