Abstract
Bulk heterojunction (BHJ) organic photovoltaic cells are analysed within a simple efficient model that includes the important physical properties of such photovoltaic systems. In this model, in contrast with most of the previous studies, we take into account the motion of both the electron and the hole in the separation process at the donor-acceptor interface. We theoretically examine the exciton dissociation yield under the influences of charge Coulomb interaction and non-radiative recombination. We find that the electron-hole local Coulomb attraction and charge carriers' coupling parameters play an important role in the system performance and in the optimal energy conversion efficiency of the BHJ photocell. We show that the fixed-hole models tend to underestimate the yield.
Export citation and abstract BibTeX RIS
Introduction
Organic photovoltaics (OPVs) [1–12] are currently a focus of intense interests because of their potential advantages, such as flexibility, low material cost, and processability [13–16]. One interesting class of OPVs is the bulk heterojunction (BHJ) cells, where the donor and acceptor zones are mixed [17–26]. In the BHJ solar cells, an absorbed photon creates a bound electron-hole pair, the so-called exciton, which migrates at the interface. After the exciton arrival at the interface and ignoring the trapping and de-trapping of charge carriers, there are two main possibilities: i) The first one is that the exciton dissociates at the donor-acceptor (D-A) interface and separated charge carriers leave the interface, then by moving along a set of acceptor and donor sites arrive at the electrodes. ii) In the second scenario the short-range and long-range Coulomb interactions between the charge carriers are strong enough, such that the charge carriers remain bound at the D-A interface [27,28]. In this second scenario, charge carriers may ultimately undergo a recombination that reduces the photovoltaic yield.
In order to investigate and subsequently improve the charge separation yield in the BHJ photocells, the material design is one important aspect. Besides, focusing on the device physics by developing models that capture the physical mechanism involved in the cell is another efficient way to improve the energy conversion yield [29–31]. In this study, we develop a simple efficient model to analyse the performance of the BHJ organic photocells. We try to pedagogically explain the main aspects of the model and use it to calculate the charge separation yield in a BHJ photocell. The yield of exciton dissociation can be treated based on this formalism by considering the effects of electron-hole interaction and non-radiative recombination. Of specific interest of this model is that both charge carriers (i.e., the electron and the hole) are considered mobile whereas in most of the studies [29,31,32], the hole is studied as a fixed carrier. We take into account the effect of electron-hole interaction either local (i.e., just at the interface) or non-local when electron and hole penetrate in the acceptor and donor zones, respectively. We also consider the possibility of non-radiative recombination processes at the interface.
The formalism developed in this paper can be compared to the model used in ref. [29]. However, among the interesting characteristics of the theoretical model developed in this manuscript is that the exciton creation, dissociation and subsequent effects on charge separation yield are discussed in the energy domain. Hence, the formalism provides useful spectral information in particular about the existence or absence of localized states which are at the heart of the exciton dissociation process. Therefore, one can discuss about the weight of excitonic states and charge separation yield and their dependence on the cell parameters. We discuss how the local and non-local interaction strength, recombination rate and coupling energies can affect the charge separation yield in the BHJ photocell. We find that the local Coulomb interaction strength and the charge coupling energies play an important role in the charge separation process.
Theoretical model
The basic idea of our methodology is shown through fig. 1(a). As can be seen, the full system includes two semi-infinite chains of acceptor (A) and donor (D) sites. For both chains, the initial sites correspond to the interface, and the rest represent the electron or hole evacuation leads. All the A and D molecules have been taken as a single level energy, corresponding to the LUMO and HOMO, respectively. For a more precise model, results obtained based on the ab initio calculations should be used. In this model, the first coupling energies to the charge evacuation chains are denoted by 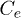 and
and 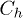 . The hopping matrix element inside each evacuation channel is considered uniform (i.e., independent of the electron-hole positions) and denoted by
. The hopping matrix element inside each evacuation channel is considered uniform (i.e., independent of the electron-hole positions) and denoted by 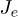 and
and 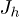 . The onsite energies are
. The onsite energies are 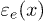 for the electron at position
for the electron at position 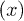 and
and 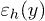 for the hole at position
for the hole at position  . The local and non-local Coulomb interaction can be taken into consideration. The interaction energy
. The local and non-local Coulomb interaction can be taken into consideration. The interaction energy  between the electron at position
between the electron at position 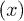 and the hole at position
and the hole at position 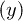 is modeled by
is modeled by

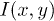 is an attractive Coulomb interaction and therefore U and V have negative values.
is an attractive Coulomb interaction and therefore U and V have negative values.
Fig. 1: (Colour online) (a) Schematic representation of a donor-acceptor system. Charge evacuation leads are considered as semi-infinite chains. Here, 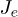 and
and  are the coupling energies between two adjacent sites in the electron and hole chains, respectively. Also,
are the coupling energies between two adjacent sites in the electron and hole chains, respectively. Also, 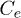 and
and 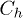 show the first coupling energies to the charge evacuation chains. (b) The square lattice representation with one state at each point
show the first coupling energies to the charge evacuation chains. (b) The square lattice representation with one state at each point 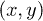 of the lattice. The coordinates x and y of a given state of the square lattice represent the positions of the electron and the hole in their respective chains. The point (0, 0) corresponds to the state in which the electron and the hole are in the LUMO and HOMO orbitals at the interface.
of the lattice. The coordinates x and y of a given state of the square lattice represent the positions of the electron and the hole in their respective chains. The point (0, 0) corresponds to the state in which the electron and the hole are in the LUMO and HOMO orbitals at the interface. 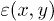 is the onsite energy of each site of the square lattice. The hopping integrals are along the binds of the square lattice and are given by the hopping integrals of electrons (respectively, holes) for the horizontal (respectively, vertical) jump.
is the onsite energy of each site of the square lattice. The hopping integrals are along the binds of the square lattice and are given by the hopping integrals of electrons (respectively, holes) for the horizontal (respectively, vertical) jump.
Download figure:
Standard imageThe Hilbert space of such a structure can be mapped onto a square lattice where 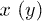 represents the position of the electron (hole) at the interface or in their respective chains (fig. 1(b)).
represents the position of the electron (hole) at the interface or in their respective chains (fig. 1(b)).
A state of the square with positions 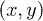 therefore represents the state where the electron is at position
therefore represents the state where the electron is at position 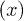 and the hole is at position
and the hole is at position 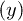 in their respective chains. Consequently, the effective Hamiltonian of the system is of the tight-binding type [33] additionally including an electron-hole interaction term
in their respective chains. Consequently, the effective Hamiltonian of the system is of the tight-binding type [33] additionally including an electron-hole interaction term

In the above equation, the first term represents the total onsite energy of each basis state and the second term is the coupling energy between two different basis states on the square lattice. The onsite energy is defined as a sum of the electron onsite energy, of the hole onsite energy and of the Coulomb interaction energy between them:

Finally we consider the possibility of electron-hole local recombination, i.e., when they are both on the site (0, 0). This is represented by adding an imaginary component −iΓ/2 to the onsite energy of site (0, 0).
In the present study, we suppose that by absorption of a photon one exciton is created in the donor side of the cell at one negative time, and then it diffuses up to the interface. This exciton arrives on site (0, 0) at time t = 0 and our aim is to evaluate the total charge injected in each contact due to the exciton dissociation after a sufficiently large time. We note Y the yield, i.e., the proportion of the electron-hole pair which gives rise to the photovoltaic current. In the absence of recombination we expect that the yield Y is related to the probability P that the excitonic state (0, 0) is in a localized state. Therefore

From this point of view, it is clear that the yield is intimately related to the spectral properties of the electron-hole Hamiltonian 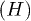 , i.e., H defined on the square lattice. More generally, we shall consider quantities such as Q:
, i.e., H defined on the square lattice. More generally, we shall consider quantities such as Q:

and
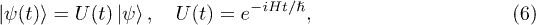
where 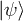 is any wave function and U(t) is the time evolution operator.
is any wave function and U(t) is the time evolution operator.
In the present study we consider 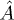 as an operator which measures the current along a bind so that Q is the total charge (in units of the electron charge) passing through a given bind during the process of exciton dissociation or recombination. Introducing the total electron number
as an operator which measures the current along a bind so that Q is the total charge (in units of the electron charge) passing through a given bind during the process of exciton dissociation or recombination. Introducing the total electron number 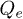 or hole number
or hole number  injected in the contacts we obtain
injected in the contacts we obtain

In order to compute or analysis the behaviour of Q we use a general relation, which relates the integrals of an operator in time and energy domains:


Here 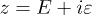 is a complex energy with an infinitesimal positive imaginary part ε and G(z) is the so-called resolvent. In the following a central quantity will be
is a complex energy with an infinitesimal positive imaginary part ε and G(z) is the so-called resolvent. In the following a central quantity will be

which is a diagonal element of the resolvent (or Green's function G(z)) on the site (0, 0). 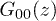 can be written as follows:
can be written as follows:

where, 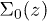 is the self-energy that can be computed based on the recursion method [34–38],
is the self-energy that can be computed based on the recursion method [34–38], 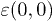 is the onsite energy of the site (0, 0) and Γ represents the rate of non-radiative recombination process of the electron-hole on site (0, 0). The local DOS for electron and hole pair is
is the onsite energy of the site (0, 0) and Γ represents the rate of non-radiative recombination process of the electron-hole on site (0, 0). The local DOS for electron and hole pair is
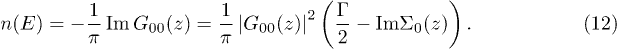
Later in this paper, we analyse the local DOS n(E) under different conditions. The characteristic behaviour of n(E) provides essential information about the existence of energy continuum and excitonic states. We define a flux of the recombination  and similarly a flux of the electron-hole pairs (Current flux)
and similarly a flux of the electron-hole pairs (Current flux)  :
:
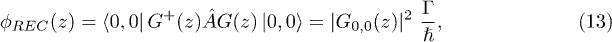

Using eqs. (12), (13), (14) one obtains

The charge separation yield, which is proportional to the portion of the charge carriers arriving to the electrodes, can be computed by the following equation:

Equation (16) is a general formula, obviously when the recombination rate is zero, the yield is simply equal to the weight of the local DOS in the energy continuum part. In that case we recover the fact that 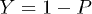 , where P is the weight of localized states.
, where P is the weight of localized states.
Results and discussion
Local density of states (DOS) without recombination
In order to analysis the exciton dissociation we first consider the spectral properties and in particular, the local DOS on the site (0, 0). Here, for the numerical simulation, we use  and
and  . The DOS is given in the unit of states per eV. With this choice of the cell parameters, the bandwidth of electrons and holes in their respective chains are 0.8 eV. Therefore, the total bandwidth of the electron-hole pair is 1.6 eV. We choose
. The DOS is given in the unit of states per eV. With this choice of the cell parameters, the bandwidth of electrons and holes in their respective chains are 0.8 eV. Therefore, the total bandwidth of the electron-hole pair is 1.6 eV. We choose

which is independent of the orbitals occupied by the electron and the hole. Since in most of the studies done so far the hole is considered as a fixed carrier, we put emphasis on the hole behaviour and its effects The approach developed here allows us to go beyond this restrictive condition (i.e., 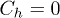 ).
).
Four values including 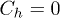 for the fixed-hole case and
for the fixed-hole case and 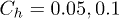 and 0.15 eV, corresponding to the mobile hole under the
and 0.15 eV, corresponding to the mobile hole under the 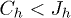 condition, are considered.
condition, are considered.
First we consider the case where there is no interaction between the electron and the hole. In that case the local DOS on site (0, 0) is the convolution of local DOS for electron and for hole on the initial sites of their respective semi-infinite chains.
When the coupling energies 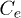 and
and 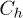 are not too strong compared to the hopping integrals
are not too strong compared to the hopping integrals 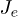 and
and 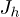 we know that the DOS for each charge carrier has a Lorentzian lineshape. Therefore, the local DOS for the electron-hole pair on site (0, 0) has also a Lorentzian lineshape with a width that is the sum of both the widths. This is consistent with the result of fig. 2 which is obtained for non-interacting charge carriers. The Lorentzian lineshape is centered at energy 2 eV which is the onsite energy of site (0, 0). In addition, as the coupling energy increases, the width of the DOS increases.
we know that the DOS for each charge carrier has a Lorentzian lineshape. Therefore, the local DOS for the electron-hole pair on site (0, 0) has also a Lorentzian lineshape with a width that is the sum of both the widths. This is consistent with the result of fig. 2 which is obtained for non-interacting charge carriers. The Lorentzian lineshape is centered at energy 2 eV which is the onsite energy of site (0, 0). In addition, as the coupling energy increases, the width of the DOS increases.
Fig. 2: (Colour online) Density of states for the electron-hole pair in non-interacting condition.
Download figure:
Standard imageFigure 3 examines the effect of the local Coulomb interaction between charge carriers at the D-A interface. We suppose the strength of the local Coulomb interaction is 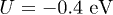 and the same values of the parameters as in fig. (2) are taken Panel (a) shows that the local interaction with
and the same values of the parameters as in fig. (2) are taken Panel (a) shows that the local interaction with 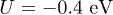 can lead to an excitonic state outside the energy continuum in the fixed-hole condition. In that case the bandwidth of the holes has no effects and only the electron bandwidth matters. Hence, the continuum of states is between 1.6 and 2.4 eV and the excitonic peak is just below the band minimum. As can be seen in panel (b),
can lead to an excitonic state outside the energy continuum in the fixed-hole condition. In that case the bandwidth of the holes has no effects and only the electron bandwidth matters. Hence, the continuum of states is between 1.6 and 2.4 eV and the excitonic peak is just below the band minimum. As can be seen in panel (b), 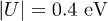 is not strong enough to generate such a localized state in the mobile-hole conditions. It can be understood based on the fact that the bandwidth of electron-hole pairs in the mobile-hole condition is between 1.2 eV and 2.8 eV. As a general statement, in order to observe an excitonic peak outside the energy continuum, the strength of interaction should be greater than a critical value (i.e.,
is not strong enough to generate such a localized state in the mobile-hole conditions. It can be understood based on the fact that the bandwidth of electron-hole pairs in the mobile-hole condition is between 1.2 eV and 2.8 eV. As a general statement, in order to observe an excitonic peak outside the energy continuum, the strength of interaction should be greater than a critical value (i.e., 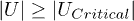 ).
).
Fig. 3: (Colour online) DOS for electron-hole pair under local interaction condition. (a) Fixed-hole case. (b) Mobile-hole cases. (c) Variation of 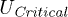 as a function of
as a function of 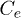 and
and 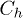 .
.
Download figure:
Standard imageMathematically an excitonic peak appears at the energy E outside the continuum, if

as shown previously by equation (11) (with 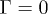 ).
).
Since 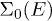 is always a decreasing function of energy outside the continuum this shows that the energy of the excitonic peak decreases when U becomes more negative. For
is always a decreasing function of energy outside the continuum this shows that the energy of the excitonic peak decreases when U becomes more negative. For 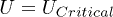 the energy of the excitonic peak takes its maximum value, i.e., just at the bottom of the continuum band
the energy of the excitonic peak takes its maximum value, i.e., just at the bottom of the continuum band 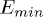 :
:
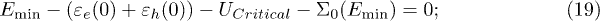
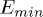 depends on the hopping integrals and the onsite energies of electron
depends on the hopping integrals and the onsite energies of electron 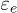 and hole
and hole  far from the interface:
far from the interface:
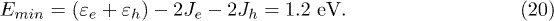
In order to have ideas about the dependence of 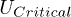 on the cell parameters, in panel (c) of fig. 2, this quantity is plotted as a function of
on the cell parameters, in panel (c) of fig. 2, this quantity is plotted as a function of 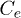 and
and 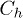 for a given set of
for a given set of 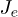 and
and 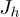 .
.
Based on the results shown in this figure, for different sets of 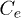 and
and 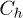 , the value of
, the value of 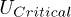 varies, but in a relatively small proportion. In fact, the limiting value of
varies, but in a relatively small proportion. In fact, the limiting value of 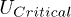 for small
for small 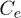 and
and 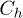 is easily obtained. Indeed, in that case eq. (19) is satisfied with the self-energy
is easily obtained. Indeed, in that case eq. (19) is satisfied with the self-energy 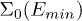 being essentially zero. Therefore, in this limit
being essentially zero. Therefore, in this limit
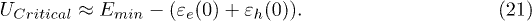
In the present case, eq. (21) gives
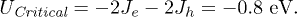
Figure 4 illustrates the interesting and more general situation with non-local Coulomb interaction between charge carriers.
Fig. 4: (Colour online) Density of states for electron-hole pair under non-local interaction condition. These figures are obtained for 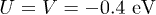 .
.
Download figure:
Standard imageIn that case we find that a series of excitonic peaks appears below the lower band of energy continuum. This is expected as it is known that the non-local Coulomb attraction creates localized states. In panels (c) and (d) in fig. 4, all the excitonic peaks close to 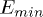 cannot be resolved.
cannot be resolved.
Excitonic weight and yield
The effect of the excitonic states on the yield Y depends on the total weight of these peaks 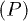 , since we have
, since we have  in the absence of recombination. In fig. 5, the total weight of the excitonic peaks under local and non-local Coulomb interaction conditions are investigated as a function of U. Here, we consider only the case of the fixed hole
in the absence of recombination. In fig. 5, the total weight of the excitonic peaks under local and non-local Coulomb interaction conditions are investigated as a function of U. Here, we consider only the case of the fixed hole 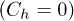 and of the symmetric coupling of electron and hole
and of the symmetric coupling of electron and hole 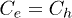 . Figure 5 depicts very similar behaviour with an abrupt variation of the total weight when U goes through some critical value. This value is not very sensitive to the non-local Coulomb interaction parameter V.
. Figure 5 depicts very similar behaviour with an abrupt variation of the total weight when U goes through some critical value. This value is not very sensitive to the non-local Coulomb interaction parameter V.
Fig. 5: (Colour online) Total weight of the excitonic peaks 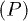 as a function of U for fixed-hole cases (a) under short-range interaction (c) under long-range interaction conditions and for symmetric coupling (b) under short-range interaction (d) under long-range interaction conditions. The strength of long-range interaction is
as a function of U for fixed-hole cases (a) under short-range interaction (c) under long-range interaction conditions and for symmetric coupling (b) under short-range interaction (d) under long-range interaction conditions. The strength of long-range interaction is 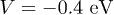 .
.
Download figure:
Standard imageTherefore, the behaviour can be understood from the case where V = 0 (panels (a) and (b)). In that case the theory predicts that the total weight of the excitonic states is P = 1 for 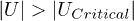 and P = 0 for
and P = 0 for  and
and 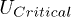 is given by eq. (21).
is given by eq. (21).
Based on the fact that the minimum energy 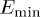 of the continuum of electron-hole pair states is not the same in the fixed-hole and the mobile-hole conditions, the variation of the
of the continuum of electron-hole pair states is not the same in the fixed-hole and the mobile-hole conditions, the variation of the 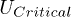 between these two situations can be understood.
between these two situations can be understood.
However, based on the results shown through these four panels one can conclude that the strength of the local Coulomb interaction U and the coupling energies are the most important parameters that can significantly affect the charge separation yield, whereas V and Γ have smaller effects.
In general, for a given electron-hole interaction the yield is much improved if the possible motion of the hole is taken into account. Therefore the mobility of the hole could be an important ingredient for much larger exciton dissociation than usually expected [39,40].
Indeed, efficient coupling to the chains facilitates the charge carrier transport and hence the possibility of localized-state appearance decreases.
Figure 6 represents the exciton dissociation yield as a function of U, for several hole coupling energy  , non-local interaction strength V and local recombination rate Γ.
, non-local interaction strength V and local recombination rate Γ.
Fig. 6: (Colour online) Yield (Y) of charge separation as a function of U obtained with different first coupling energies to the hole chain. The legend presented in the first panel, is valid for all the other panels. Γ represents the decay parameter and V is the strength of long-range interaction.
Download figure:
Standard imageOur results show that by considering the hole as a fixed carrier, since  is underestimated, the yield of the cell has a smaller value, particularly for low recombination rate.
is underestimated, the yield of the cell has a smaller value, particularly for low recombination rate.
In general, one can conclude that the effect of non-radiative recombination is to reduce the yield, and its impact is more significant in the charge local interaction condition.
In fact, in relaxation processes, less charge carriers are able to exit through the electrodes, hence the yield decreases.
Conclusion
In this study, we have used a simple efficient model to examine the performance of BHJ organic photovoltaic cells under different conditions. In particular, we propose an analysis based on the energy spectrum of the electron-hole pair. Our results show that the yield strongly depends on the local interaction energy strength U. There is a critical interaction energy 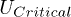 , which depends essentially on the band edges of the electron-hole excitations, and the HOMO-LUMO energy offset on the initial site. We find that if
, which depends essentially on the band edges of the electron-hole excitations, and the HOMO-LUMO energy offset on the initial site. We find that if 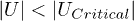 yield values are higher compared to the
yield values are higher compared to the 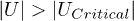 case where the localized states are created and hence the yield is strongly decreased. In addition, we have investigated the effect of the hole propagation. Our results show that by considering the hole as a fixed carrier, one underestimates
case where the localized states are created and hence the yield is strongly decreased. In addition, we have investigated the effect of the hole propagation. Our results show that by considering the hole as a fixed carrier, one underestimates 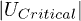 . Therefore, in the fixed-hole model, the yield of the cell can be underestimated, particularly for low recombination rate. Hence, the mobility of the hole is an important parameter to improve the exciton dissociation yield.
. Therefore, in the fixed-hole model, the yield of the cell can be underestimated, particularly for low recombination rate. Hence, the mobility of the hole is an important parameter to improve the exciton dissociation yield.
Acknowledgments
We would like to acknowledge the financial support provided by Campus France and the French embassy in Tehran. Furthermore, the financial support through the Institut Néel is acknowledged.











