Abstract
Encouraged by the interaction between two species of microbes, in which one species is capable of replenishing the public resources and the other is not, the dilemma structure (the long-term sustainability of the population) hidden in a system where public goods are defined as diffusible was examined. In a series of simulations in which the three major parameters governing the dynamics of the system were varied, following the effect of the spatial structure that results from resource diffusion and distribution, the dynamics show a rich diversity, including cooperator-dominated, extinct, and coexistent results. If the dilemma is strong, the chance of surviving cooperators is small and the population tends to extinction even though coexistence is possible. By contrast, if a weak dilemma is given, the affluent resources make cooperators dominant over defectors.
Export citation and abstract BibTeX RIS
Introduction
A public goods game (hereafter PGG) can be used not only in economics but also in several interdisciplinary fields [1]. Mathematically, the PGG is a dilemma game classified as a multi-player Prisoner's Dilemma (n-Prisoner's Dilemma or n-PD) game [2]. An agent can adopt one of two strategies: Cooperation (C) or Defection (D). A cooperator (or C agent) offers to invest a certain amount of their funds (called a cost) into a common pool. The cumulative investment dedicated by the cooperators is multiplied by r, and this amplified benefit is distributed to all participants equally, irrespective of their strategies. Therefore, adopting the D strategy and taking a free ride on the benefits must dominate even though the system will collapse if all do the same (the tragedy of commons [3]).
The dilemma situation associated with the PGG is observed in the world of microbes [4–7]. It is well known that the species Saccharomyces cerevisiae, a type of budding yeast, helps others by producing invertase enzymes that hydrolyze sucrose to fructose and glucose. This monosaccharide (glucose and fructose) provided by hydrolysis is a necessary resource for the survival of the other types of yeast and is distributed via diffusion through the nutrient medium. In essence, it can be said that S. cerevisiae produces public goods and the others free ride. The relationship between the two types of microbes resembles the roles of the cooperator (donor) and the defector (recipient) in a social dilemma game. Therefore, when they appropriately account for the diffusion of "public goods" or resources in a field, PGGs may fairly describe this particular social dilemma in the world of microbes. Several previous studies have reported that the dynamics of resource diffusion can be interpreted as a redistribution of public goods, which has led to the establishment of advanced PGG models including mathematical models and cell automaton models [8–16]. Note that this system is not entirely defined as the class of PD, snow-drift result is also reported [17–19].
Most notable is a study by Allen et al. [11]. Allen et al. proposed a mathematical model to describe the social dilemma observed between the two types of microbes mentioned above, S. cerevisiae and its follower (or free rider) as a generalized PGG in which the dilemma structure, amazingly, is consistent with the inequality associated with network reciprocity Specifically, cooperation is favored only when the benefit-to-cost ratio is larger than the network degree b/c > k, a condition that Nowak proved to be one of the five fundamental mechanisms of "social viscosity" [20]. One novel point Allen identified is that the resource diffusion can be modeled by a transformed relation between the vertices connected by an edge, i.e., a network relation.
Despite its novelty, Allen et al.'s study seems less appropriate when applied to a general social dilemma, perhaps one universally applicable in the sphere of microbes, because, in their model, a cooperator can maintain a constant resource production rate irrespective of its inner metabolic level. It would be more appropriate if a cooperative-minded agent could not dedicate resources when exposed to a meager environment, while being able to behave in a fully cooperative manner when faced with abundant primary resources in its environment. In other words, the Allen model potentially assumes a system with two unique resources, where the cooperator relies on a different primary resource than the resource that both cooperators and defectors consume to enhance their fitness.
This study addresses a mono-resource system as opposed to a multi-resource system, and therefore defines only a single resource. Any agent can use this resource for survival, but a cooperator uses some part of the resource it imports from its environment to amplify it by means of an anabolic mechanism, and subsequently releases the product, which then diffuses throughout the field. We establish a new mathematical model and examine how rich phases can result. We investigated whether the population, which shares the resource through diffusion, goes extinct like the tragedy of commons or builds a sustainable system.
This report is organized as follows: the second section provides the model framework, the third section shows the preliminary results, the fourth section gives the simulation results and discussion, with a particular focus on the contour map, and we conclude in the last section.
Models and methods
We aimed to establish a general model for the evolutionary process of a species of microbes living on a plate of agar gel. Each microbe puts down its roots at a certain location in the 2-dimensional (2D) agar gel. The microbes therefore do not move on the gel, but rather the resource diffuses through the gel according to the archetypal 2D diffusion equation. We can define the concentration of the resource at any place on the gel. The microbes can be divided into two categories. The first is the defective type (hereafter called defectors, D), which consumes a certain amount of the resource by absorbing it from the gel. The second is the cooperative type (hereafter called cooperators, C), which likewise consumes the resource but simultaneously replenishes the resource through a specific anabolic effect. The resource, produced in this way, is released into the gel. For simplicity, this study assumes that the only evolutionary process that takes place is in the turnover of single individuals, and that the evolutionary process of cell division that results in the growth of the microbe colony into the surrounding vacant space does not occur.
We describe the details of this model below.
Mathematical model of diffusible public goods
We assume a 2D gel space divided into N (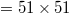 ; see fig. 1) von Neumann cells. We initially place n0 (
; see fig. 1) von Neumann cells. We initially place n0 ( ; see fig. 1) microbes in the center of the gel region in a diamond formation as shown in fig. 1. Each microbe occupies a single cell of the gel. We express the address of a cell as an index i, and assume a concentration of the resource in that cell
; see fig. 1) microbes in the center of the gel region in a diamond formation as shown in fig. 1. Each microbe occupies a single cell of the gel. We express the address of a cell as an index i, and assume a concentration of the resource in that cell  . The strategy (C or D) of an agent located in cell i is denoted as
. The strategy (C or D) of an agent located in cell i is denoted as  . A cooperator (C:
. A cooperator (C:  ) produces and releases the resource P into its own cell. In contrast, a defector (D:
) produces and releases the resource P into its own cell. In contrast, a defector (D: 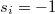 ) cannot produce the resource. Any arbitrary agent consumes a quantity of the resource, Mi, to maintain its fundamental metabolism. Denoting the equivalent overall diffusion coefficient as Λ, the governing equation can be written as follows:
) cannot produce the resource. Any arbitrary agent consumes a quantity of the resource, Mi, to maintain its fundamental metabolism. Denoting the equivalent overall diffusion coefficient as Λ, the governing equation can be written as follows:
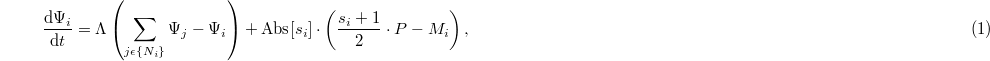
where 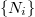 indicates the set of four von Neumann cells neighboring cell i.
indicates the set of four von Neumann cells neighboring cell i.
Fig. 1: Computational domain and cell positions. Initially,  agents are assigned in a diamond-shaped region in the center of the domain, where C (gray) and D (black) agents are randomly placed. The resource can flow out through the boundaries.
agents are assigned in a diamond-shaped region in the center of the domain, where C (gray) and D (black) agents are randomly placed. The resource can flow out through the boundaries.
Download figure:
Standard imageAn agent, irrespective of its strategy, imports the resource, which depends on the intake efficiency μ and the concentration difference between  and
and  , where
, where  represents the internal resource concentration of agent i. The resource intake must at least equal the basal metabolism
represents the internal resource concentration of agent i. The resource intake must at least equal the basal metabolism  . Thus, we can evaluate Mi as follows:
. Thus, we can evaluate Mi as follows:

An agent dies and is removed from the cell whenever it cannot import more than  from the cell in which it lives.
from the cell in which it lives.
A cooperator devotes a part of its intake resources to resource production. We presume that a cooperator invests the maximum possible amount in this process,  , which must also be no less than the Cost, which is the minimum requisite resource amount required to activate the anabolic effect. Our normalization in this study assumes
, which must also be no less than the Cost, which is the minimum requisite resource amount required to activate the anabolic effect. Our normalization in this study assumes  . In short, the amount invested by the cooperator i is Min[Cost, Mi − Mmin]. The quantity of the resource produced, P, is given as the product of the investment and the productivity parameter b, which corresponds to the dilemma weakness. Thus, we get
. In short, the amount invested by the cooperator i is Min[Cost, Mi − Mmin]. The quantity of the resource produced, P, is given as the product of the investment and the productivity parameter b, which corresponds to the dilemma weakness. Thus, we get

The fitness of agent i, 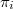 , which stipulates its evolutionary strength, depends on whether it is cooperative or defective as follows:
, which stipulates its evolutionary strength, depends on whether it is cooperative or defective as follows:

Death-birth process
Stochastic adaptation processes occur in microbe populations. In this study, we adopt a death-birth process to replicate an agent's evolutionary process [21]. At each discrete step, a randomly selected agent dies and is removed. Simultaneously, one of the agents in the neighboring von Neumann cells (if there are any) is selected according to its fitness to produce a new offspring that refills the vacant cell. This offspring inherits its parent's strategy. If there are no neighbors, the cell remains vacant. Therefore, by performing this reproduction process based on a fitness evaluation, a dynamics occurs that results in a changing strategy profile in the system. If at any point only defectors remain, the evolutionary episode eventually ends in extinction, as the resource is not being replenished in the domain.
Simulation setting
In each episode, the initial resource is distributed to those cells to which an agent has been initially assigned, i.e., in the diamond formation mentioned above and shown in fig. 1. The initial concentration is denoted as 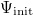 . According to the diffusion equation in eq. (1), the initial resource distribution spreads over time. Let us assume that each boundary of the domain adopts the free-boundary condition (in other words, the concentration outside the domain is always maintained at zero), so that the resource can freely flow out. Therefore, if no cooperators remain in the domain, sooner or later the resource will run out and all of the agents will go extinct.
. According to the diffusion equation in eq. (1), the initial resource distribution spreads over time. Let us assume that each boundary of the domain adopts the free-boundary condition (in other words, the concentration outside the domain is always maintained at zero), so that the resource can freely flow out. Therefore, if no cooperators remain in the domain, sooner or later the resource will run out and all of the agents will go extinct.
To provide a numerical solution for the diffusion equation, the so-called explicit method for time is applied. The fundamental parameters are set to 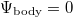 ,
,  ,
,  , and
, and  , and the control parameters are the following: the diffusivity of the resource Λ, the intake efficiency μ, and the dilemma weakness b. Moreover, from the point of what features public good games with diffusion express, to avoid the complexity resulting from the increase of population size, mutation is not considered (mutation rate 0% is assumed).
, and the control parameters are the following: the diffusivity of the resource Λ, the intake efficiency μ, and the dilemma weakness b. Moreover, from the point of what features public good games with diffusion express, to avoid the complexity resulting from the increase of population size, mutation is not considered (mutation rate 0% is assumed).
In the following text, we discuss the equilibrium configuration that is achieved for a specific set of control parameter values as a result of the competitive dynamics between C and D. Specifically, starting from a state with an equal number of Cs and Ds 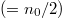 randomly placed in the diamond area in fig. 1, we determine whether cooperators ultimately dominate, defectors dominate, or both species coexist. Again, the state of defector domination (an all-defectors-state) is not sustainable and results in eventual extinction as no more of the resource is produced in the domain. Meanwhile, coexistence means that defectors can successfully free ride on the work of cooperators, and this is defined as a situation in which both C and D agents survive after an appropriately large number of time iterations (200000 time steps).
randomly placed in the diamond area in fig. 1, we determine whether cooperators ultimately dominate, defectors dominate, or both species coexist. Again, the state of defector domination (an all-defectors-state) is not sustainable and results in eventual extinction as no more of the resource is produced in the domain. Meanwhile, coexistence means that defectors can successfully free ride on the work of cooperators, and this is defined as a situation in which both C and D agents survive after an appropriately large number of time iterations (200000 time steps).
By performing 300 independent trials, we obtained an ensemble average value for the statistics The result was obtained for various sets of the three parameters by varying the initial cooperation fraction.
Preliminary results
Before reporting the simulation results of competition for the two species, to ensure the inherent sustainability of the population, we first conducted simulations to determine whether a population consisting of only cooperators could survive for various initial population densities ρ. Specifically, starting from a certain ρ in which Cs are randomly assigned in the diamond in fig. 1, we examined how many realizations of the 300 trials allowed the population to survive. The result, presented as the average frequency of extinction for each dilemma strength, is shown in fig. 2. In both figs. 2(A1) and (B1), we can clearly see that the population can survive in most of the parameter range, except when μ is very close to 0. This implies that too small a μ does not allow even cooperators to survive due to the lack of sufficient nutrition. From the indicated values at the two cross-marks in the panels, we can see that fig. 2(A1), which assumed the stronger dilemma, has a slightly higher possibility of extinction. Examining the details in figs. 2(A2) and (B2), we see that the population is more likely to go extinct when assuming a smaller initial population density. Moreover, in fig. 2(A2), which assumes the stronger dilemma, depending on the diffusivity of the public goods, the extinction frequency increases even when a reasonably large initial population density is given. This implies that even without exploiting agents, the cooperators cannot maintain their population by diffusing the resource out into the surrounding space. This study does not take into account the increasing number of agents in an episode from the viewpoint of exploring the inherent system dynamics brought on by the public goods diffusion; however, if we were to consider this, the possibility of the population surviving would be slightly higher.
Fig. 2: (Colour online) The frequency of extinction for different dilemma strengths for 300 independent trials when the population is made up of only C agents. The average frequency of extinction in the Λ-μ plane is (A1) 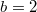 and (B1)
and (B1)  , where the arithmetic average value for the initial population density ρ varying in the range of [0, 1] is used. The numerical values of the marked crosses indicate actual frequencies. (A2) and (B2) show the frequencies of extinction in the Λ-ρ plane, where
, where the arithmetic average value for the initial population density ρ varying in the range of [0, 1] is used. The numerical values of the marked crosses indicate actual frequencies. (A2) and (B2) show the frequencies of extinction in the Λ-ρ plane, where 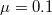 is assumed, and varying Λ is shown by the red dotted line in (A1) and (B1), where for (A2)
is assumed, and varying Λ is shown by the red dotted line in (A1) and (B1), where for (A2)  and for (B2)
and for (B2) 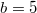 .
.
Download figure:
Standard imageResults and discussion
In this section, we discuss the social dilemma structure in public goods games with diffusion, namely, whether or not the population survives as a result of competition between two species.
Under a particular parameter set for Λ, μ, and b, we can compile statistics, expressed by the frequency of Extinction (either true extinction or only defectors surviving), Polymorphic (co-existing cooperators and defectors), or Cooperation (cooperator dominating the system) results over 300 independent simulation trials while varying the initial cooperation fraction. In a typical illustration, fig. 3 shows the equilibrium frequency distribution. In observing fig. 3(A), we can see that extinction is prevalent and does not depend on the initial cooperation fraction (hereafter Pc_init). However, when most agents are C (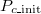 is close to 1), this is not true. The frequency of cooperation exceeds that of extinction, which is inevitable because the stochastic adaptation process of death-birth is adopted. We classify this case as Extinction. In fig. 3(B), even though we can confirm that the system reaches various equilibriums according to the
is close to 1), this is not true. The frequency of cooperation exceeds that of extinction, which is inevitable because the stochastic adaptation process of death-birth is adopted. We classify this case as Extinction. In fig. 3(B), even though we can confirm that the system reaches various equilibriums according to the 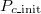 , intermediate
, intermediate 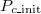 values show a high probability of a coexistent equilibrium. In addition, frequent Cooperation (Extinction) is seen in the range of high (low)
values show a high probability of a coexistent equilibrium. In addition, frequent Cooperation (Extinction) is seen in the range of high (low) 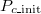 . This complex tendency results from the subtle power balance between C and D due to this particular parameter set and
. This complex tendency results from the subtle power balance between C and D due to this particular parameter set and 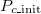 . If C is small, it is hard to maintain the population because either C or D is inevitably weeded out. Conversely, a sufficient number of cooperators results in a sustainable system. This phase is called Polymorphic. Figure 3(C), contrary to fig. 3(A), shows consistent cooperation; however, the effect of the stochastic process is still observed. In fact, assuming a small initial cooperator density leads to frequent extinction and a sustainable system is rarely realized.
. If C is small, it is hard to maintain the population because either C or D is inevitably weeded out. Conversely, a sufficient number of cooperators results in a sustainable system. This phase is called Polymorphic. Figure 3(C), contrary to fig. 3(A), shows consistent cooperation; however, the effect of the stochastic process is still observed. In fact, assuming a small initial cooperator density leads to frequent extinction and a sustainable system is rarely realized.
Fig. 3: Frequency of the three possible equilibria of the 300 independent trials for different initial cooperation fractions 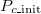 with constant initial population density
with constant initial population density 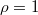 : (A) Extinction (
: (A) Extinction (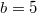 ,
, 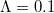 ,
, 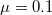 ), (B) Polymorphic (
), (B) Polymorphic (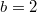 ,
,  ,
,  ); and (C) Cooperation (
); and (C) Cooperation (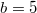 ,
, 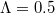 ,
,  ). Here the square, circle, and triangular symbols show the frequency of each equilibrium: extinction, cooperation, and coexistence (Polymorphic), respectively.
). Here the square, circle, and triangular symbols show the frequency of each equilibrium: extinction, cooperation, and coexistence (Polymorphic), respectively.
Download figure:
Standard imageIn the subsequent section, we will examine what phases can be observed when the three parameters, Λ, μ, and b are varied.
In fig. 4, we see the average frequency of each equilibrium state defined by the above-mentioned procedure for fig. 3, as well as a phase diagram represented by the most dominant equilibrium (e.g., see ref. [12]).
Fig. 4: The frequency of each equilibrium and the phase diagrams of the dynamics drawn in the Λ-μ plane for different dilemma strengths. The fixed parameter for (A) and (C) is  and for (B) and (D) is
and for (B) and (D) is 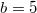 . Panels (A) and (B) show the equilibrium frequency for cooperation, coexistence, and extinction with varying initial cooperation fractions with
. Panels (A) and (B) show the equilibrium frequency for cooperation, coexistence, and extinction with varying initial cooperation fractions with 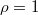 . The numerical values in the panels indicate the actual frequency at the settings indicated by the cross-marks. Panels (C) and (D) show phase diagrams of the dynamics based on Panels (A) and (B), where only the frequency of the most frequent equilibrium is represented and coexistence is labeled as Polymorphic.
. The numerical values in the panels indicate the actual frequency at the settings indicated by the cross-marks. Panels (C) and (D) show phase diagrams of the dynamics based on Panels (A) and (B), where only the frequency of the most frequent equilibrium is represented and coexistence is labeled as Polymorphic.
Download figure:
Standard imageStrong dilemma
As shown in fig. 4(C), the phase transition (C-dominated →Polymorphic→ D-dominated) takes place in a sequential manner with increasing diffusivity and is more obvious than in the case of a weak dilemma, as in fig. 4(D) and discussed below. If the resource spreads slowly throughout the domain with a smaller diffusivity, a cooperator will have access to a relatively large quantity of the resource, whereas a defector who relies on the resource flowing from the surrounding cooperators will have a more difficult time. This means that the fitness of the cooperators naturally exceeds that of the defectors and the cooperators' offspring will ultimately dominate the population. Consequently, C-domination emerges. If the resource diffuses reasonably quickly throughout the domain, defectors can more easily obtain the resources provided by the cooperators, which allows defectors to free ride on the work of the cooperators, leading them to produce offspring. However, the continued existence of cooperators is requisite for the survival of the defectors. Because both types of agents can coexist without extinction, a Polymorphic phase occurs. That is, the cooperators form a cluster and produce abundant resources with mutual cooperation, while the defectors obtain little resources at a distance. Accordingly, once the parameter balance collapses, the equilibrium state is pulled into either the Cooperation or Extinction phases. If the resource diffuses too quickly, the defectors become completely dominant, and the cooperators are replaced. This is because it is harder for a cooperator to keep the resource it produces for itself, and it must pay a production cost. In this case, the entire population eventually goes extinct because the complete absence of cooperators is not sustainable. In other words, "a society of free riders with no tax-payers goes to ruin."
Weak dilemma
In fig. 4(D), by improving the productivity and therefore relaxing the dilemma strength, a tendency for Cs to prosper more than Ds is observed. In general, both low diffusivity and high intake rates work in favor of survival for cooperators, as was observed in the strong dilemma case. This means that the Polymorphic phase observed between the Cooperation and Extinction cases in fig. 4(C) disappears because the relaxed dilemma favors cooperation; therefore, no free riders survive in the system as long as a smaller diffusivity is assumed. This is why the Coexistence fraction is very small in fig. 4(B). Along with the relaxed dilemma from 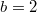 to
to 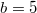 , the coexistent results decrease with gradual manner. If one increases the diffusivity, despite the weaker dilemma, the dynamics suddenly shift from Cooperation to Extinction. As the social dilemma gets weaker than
, the coexistent results decrease with gradual manner. If one increases the diffusivity, despite the weaker dilemma, the dynamics suddenly shift from Cooperation to Extinction. As the social dilemma gets weaker than 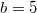 , it is expected that the Cooperation phase will enlarge and the Extinction phase will diminish. In general, the system favors one of the two extreme equilibria, either Cooperation or Extinction, and is much less likely to adopt a "cloudy" equilibrium, such as the Polymorphic phase. Therefore, realizing a sustainable system implies an all-cooperators-state and does not allow defectors to survive.
, it is expected that the Cooperation phase will enlarge and the Extinction phase will diminish. In general, the system favors one of the two extreme equilibria, either Cooperation or Extinction, and is much less likely to adopt a "cloudy" equilibrium, such as the Polymorphic phase. Therefore, realizing a sustainable system implies an all-cooperators-state and does not allow defectors to survive.
Conclusion
To reveal the underlying dilemma structure in a public goods game (PGG) in which the "public goods" diffuse throughout the system, we developed a new PGG model to reproduce the struggle between cooperators, who replenish a resource, and defectors, who free ride on the productivity of the cooperators.
To ensure sustainability at a certain level, preliminary simulations assuming that the population is composed entirely of cooperators were conducted. We confirmed that the population could be sustained, except when there was a small initial population density, and variations were observed due to the effect of diffusivity.
Our numerical simulations resulted in phase diagrams where the diffusivity, the intake rate of the resource, and the dilemma strength were all varied. Despite the payoff function based on the PGG, the effect of the spatial structure (the diffusion and concentration distribution) resulted in very different outcomes from those estimated from the payoff function, i.e., Cooperation, Polymorphic, and Extinction phases. We found that a stronger social dilemma requires a small diffusivity to maintain the population because the produced resources are very small. That is, fast diffusion encourages the survival of defectors, and a sustainable population cannot be achieved. An intermediate diffusivity establishes a symbiotic relationship, namely, clustering cooperators produce large quantities of resources and a few defectors get a free ride. A weaker social dilemma not only favors cooperation but also discourages "cloudy" equilibria, such as the Polymorphic phase, in favor of "clear" equilibria, either C-dominated or D-dominated.
As mentioned in the text, the presented model assumes that the only evolutionary process taking place is in the turnover of individual agents and disregards another important evolutionary process, cell division, which results in the growth of the microbe colony into the surrounding vacant space. In addition, it is expected that the number of individuals will express fluctuations, such as those seen in Lotka-Volterra systems. In the beginning of each episode in such a system, defectors overtake cooperators and population size diminishes due to die outs. In the next stage, cooperators in clusters generate new individuals with ample resources and the population size grows. However, defectors again exploit the cooperators and increase in number; and the decrease in the population size is repeated. In this way, a certain sustainability, as seen in biological systems, can be produced. This type of system will be examined further in a subsequent report.
Acknowledgments
This study was partially supported by a Grant-in-Aid for Scientific Research from JSPS, Japan, awarded to JT (Grant No. JP15K14077). In addition, we would like to express our gratitude to Dr Eriko Fukuda for several interactive discussions.









