Abstract
The vacuum breakdown process in an inhomogeneous supercritical electric field of finite extension is examined. By probing the electron-positron pair creation zone with incoming electrons that have controlled velocities, we can address the fundamental question of where the electrons are being created from the vacuum. In contrast to what one might expect, the spatial regions of most likely pair creation are not necessarily those where the electric-field strength is largest. In fact, the creation regions are determined solely by energetic considerations and particles can therefore be created in spatial regions where the local field strength is far below the Schwinger threshold. These predictions are also supported independently by spatial probability densities obtained by extrapolation as well as by classical and quantum-mechanical analysis.
Export citation and abstract BibTeX RIS
It has been predicted for quite some time that a sufficiently intense electromagnetic radiation pulse or even a static electric field can break down the vacuum and trigger the creation of electron-positron pairs [1,2]. Due to the possibility of new experimental work at various laser laboratories worldwide [3], exploring various field configurations to maximize the yield for this process has become a hot topic of wide theoretical interest. A major benchmark for the occurrence of this intriguing pair creation mechanism is the Schwinger critical electrical field [4]. For this threshold to serve as valid quantitative criterion, however, one has to assume implicitly that the particles are actually created in those spatial regions where the electric force is maximal. In this letter we will present independent arguments that suggest that the pair creation rate does not necessarily correlate with the electric force field. In fact, there can be spatial regions in supercritical inhomogeneous field configurations where the electric field is largest but not a single electron is created, while at the same time the particle production rate can be maximum in regions of smaller force.
The fundamental question of how to unambigously identify particles as well as their precise birth location inside the interaction zone has been a challenge in theoretical physics. Most analysis so far relied on projections onto force-free energy eigenstates to "define" what constitutes a real particle.
Here the relativistic 2mc2 mass gap provides the criterion to distinguish between electrons and positrons. This energy-based distinction, however, becomes problematic if the external force is sufficiently strong (supercritical), such that states of the lower and upper energy manifolds are shifted and overlap. This resulting degeneracy is predicted to be directly associated with the permanent creation of particles. Therefore, it has been difficult to uniquely identify particles inside the interaction zone. Important physical quantities such as number of particles or their energy spectrum are thought to become only unambigous after the particles have left the creation region.
There are only a few works that have tried to examine different projections in order to identify particles. Gerry et al. [5] have used dressed states but for a special case in which the particles were created exclusively due to a time-dependent electric field. A similar scenario was studied in 2010 by Mocken et al. [6]. During the same year, Hebenstreit et al. [7] provided space-resolved information using a Wigner function formalism.
In this letter we propose several novel means that allow us for the first time to gain information about the spatial distribution of the produced particles inside of this "black-box" interaction region in the steady-state regime. They allow us to zoom into the pair creation zone and consistently predict that a) there exist production-free regions independent of the local strength of the force field and b) particles are not necessarily created where the force is maximal. The first approach probes the inhomogenous field configuration with electronic wave packets exploiting dynamical Pauli blocking. The second approach computes the spatial charge density directly by a suitable extrapolation method. The third approach correlates the kinetic-energy spectrum of the emitted electrons to the respective spatial distribution of birth locations. The fourth approach shows that a classical model without any adjustable parameters predicts a similar spatial distribution. The fifth approach generalizes the quantum-mechanical tunneling picture.
As numerous works have described the technical details of solving the Dirac equation for the (second-quantized) electron-positron field operator to simulate pair creation on space-time grids [8], we focus here entirely on the results. To illustrate that mechanisms other than the local force strength play a role, we model the supercritical zone here by a region between 0 < z < w where the amplitude of the electric field is constant. This simplified configuration can be described by a one-dimensional linear potential 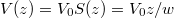 for 0 < z < w,
for 0 < z < w,  for z < 0 and
for z < 0 and 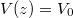 for w < z. The Schwinger rate [4] assumes that the yield depends on the electric-field amplitude and would (incorrectly) suggest that the particles for our configuration should be created uniformly in the entire zone 0 < z < w. However, we will see below that electrons can be only created in the narrower range
for w < z. The Schwinger rate [4] assumes that the yield depends on the electric-field amplitude and would (incorrectly) suggest that the particles for our configuration should be created uniformly in the entire zone 0 < z < w. However, we will see below that electrons can be only created in the narrower range  , in which the creation rate even depends on the location, despite the force being constant between 0 < z < w.
, in which the creation rate even depends on the location, despite the force being constant between 0 < z < w.
The first proposal to probe the interaction zone  uses the dynamical Pauli suppression [9,10], which is based on the fact that two fermions cannot share the same quantum state including the spin. Correspondingly, states that are occupied by an incoming electron are blocked from pair creation until the electron leaves the interaction zone. We have injected a narrow Gaussian-shaped electron wave packet into the electric-field region. Before and after the electron probes the interaction zone, the supercritical barrier (
uses the dynamical Pauli suppression [9,10], which is based on the fact that two fermions cannot share the same quantum state including the spin. Correspondingly, states that are occupied by an incoming electron are blocked from pair creation until the electron leaves the interaction zone. We have injected a narrow Gaussian-shaped electron wave packet into the electric-field region. Before and after the electron probes the interaction zone, the supercritical barrier (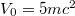 and
and 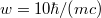 ) generates a constant out-flux of particle pairs resulting in a linear increase of the number of particles in time
) generates a constant out-flux of particle pairs resulting in a linear increase of the number of particles in time 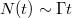 , where Γ (= 17.75 atomic units for our parameters) denotes the total pair creation rate. Each incoming velocity corresponds to a position
, where Γ (= 17.75 atomic units for our parameters) denotes the total pair creation rate. Each incoming velocity corresponds to a position 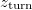 , where the wave packet narrows significantly and comes momentarily to rest before it accelerates out of the interaction zone. If we assume that the particles are created at rest, the incoming electron can Pauli-block (and therefore probe) the creation process for an electron with the same spin only at this turning point
, where the wave packet narrows significantly and comes momentarily to rest before it accelerates out of the interaction zone. If we assume that the particles are created at rest, the incoming electron can Pauli-block (and therefore probe) the creation process for an electron with the same spin only at this turning point 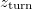 . By subtracting the reduced yield N(t) from that without any incoming electron, we can determine the amount of permanent suppression due to the electron, denoted by the offset
. By subtracting the reduced yield N(t) from that without any incoming electron, we can determine the amount of permanent suppression due to the electron, denoted by the offset 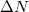 .
.
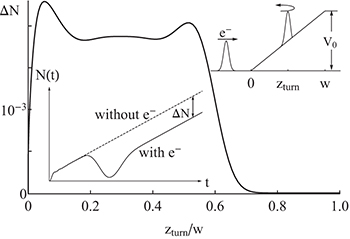
In fig. 1 we have graphed the offset 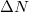 as a function of the turning point of the electron
as a function of the turning point of the electron  . The amount of suppression depends strongly on this position and seems maximal around
. The amount of suppression depends strongly on this position and seems maximal around  and
and 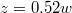 . Furthermore, the probing electron has apparently no permanent impact on the yield in about 40% of the zone
. Furthermore, the probing electron has apparently no permanent impact on the yield in about 40% of the zone 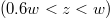 , suggesting the absence of any pair creation, despite the presence of the constant force in that region.
, suggesting the absence of any pair creation, despite the presence of the constant force in that region.
Fig. 1: The (permanent) reduction in the particle number 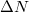 due to an incoming electron that is injected into the interaction zone. Its incoming velocities were varied such that the electron's turning points
due to an incoming electron that is injected into the interaction zone. Its incoming velocities were varied such that the electron's turning points  can probe the pair creation region 0 < z < w, while its spatial width was much smaller than w to provide spatial resolution. [
can probe the pair creation region 0 < z < w, while its spatial width was much smaller than w to provide spatial resolution. [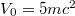 ,
, 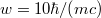 .]
.]
Download figure:
Standard imageAs a second and more direct proof of the zero-electron production region 0.6w < z, we have calculated the spatial probability distribution of the created electrons 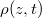 , defined as the expectation value in the vacuum state
, defined as the expectation value in the vacuum state 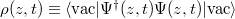 , where Ψ denotes the electronic portion of the electron-positron field operator [11]. This density can be re-written as a function of the time-evolved states
, where Ψ denotes the electronic portion of the electron-positron field operator [11]. This density can be re-written as a function of the time-evolved states 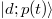 of initial momentum p, as
of initial momentum p, as 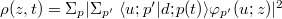 . These energy eigenstates fulfill
. These energy eigenstates fulfill 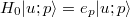 and
and 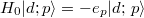 with
with ![$e_{p}\equiv[m^{2}c^{4}+c^{2}p^{2}]^{1/2}$](https://content.cld.iop.org/journals/0295-5075/116/4/40003/revision1/epl18272ieqn28.gif) and have the spatial representation
and have the spatial representation  . The force-free Dirac Hamiltonian is given by
. The force-free Dirac Hamiltonian is given by  with the two
with the two  Pauli matrices
Pauli matrices 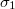 and
and 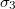 .
.
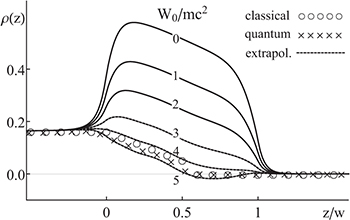
After the turn-on of the supercritical field, the particles grow first in the force region and then approach a steady state that is characterized by a constant density for z < 0, corresponding to a permanent flux of left-going electrons and a vanishing electron density ρ for w < z. For z < 0, the constant density ρ (= 0.158 a.u. for our case) is equal to the product of the electron creation rate 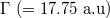 and the inverse of the average speed of the ejected particles
and the inverse of the average speed of the ejected particles 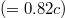 . This is shown by the top curve in fig. 2 (labeled by
. This is shown by the top curve in fig. 2 (labeled by 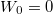 ).
).
Fig. 2: The spatial probability density of the created electrons 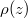 in the steady state. The densities differ by the states that were used to define the electronic portion of the field operator.
in the steady state. The densities differ by the states that were used to define the electronic portion of the field operator.  corresponds to the traditional basis of force-free energy eigenstates. The three dashed lines (
corresponds to the traditional basis of force-free energy eigenstates. The three dashed lines (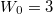 , 4 and 5mc2) were obtained by extrapolation. (Same parameters as in fig. 1.)
, 4 and 5mc2) were obtained by extrapolation. (Same parameters as in fig. 1.)
Download figure:
Standard imageInside the supercritical region 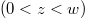 , however, the quantity
, however, the quantity 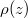 does not represent any physical electrons, as its very definition was based on force-free states, which are hard to interpret in this region. In fact,
does not represent any physical electrons, as its very definition was based on force-free states, which are hard to interpret in this region. In fact, 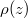 describes strictly only real electrons, if the force is turned off abruptly at time t and, therefore, contains the possible annihilation or creation due to this temporal change of the force [5]. In order to improve the traditional H0-based [4] definition of
describes strictly only real electrons, if the force is turned off abruptly at time t and, therefore, contains the possible annihilation or creation due to this temporal change of the force [5]. In order to improve the traditional H0-based [4] definition of 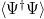 we can alternatively define the electronic portion of the electron-positron field operator by projecting on the dressed energy eigenstates of the Hamiltonian
we can alternatively define the electronic portion of the electron-positron field operator by projecting on the dressed energy eigenstates of the Hamiltonian 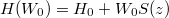 . Here the shape of the potential S(z) is the same as that used for the dynamics except for a smaller amplitude, denoted by W0. Note that as long as this potential is subcritical
. Here the shape of the potential S(z) is the same as that used for the dynamics except for a smaller amplitude, denoted by W0. Note that as long as this potential is subcritical 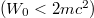 , there is a mass gap that permits us to separate the spectrum (and therefore the field operator) unambiguously into electronic and positronic portions. The next two electronic steady-state densities in fig. 2 were computed for exactly the same supercritical dynamics (with
, there is a mass gap that permits us to separate the spectrum (and therefore the field operator) unambiguously into electronic and positronic portions. The next two electronic steady-state densities in fig. 2 were computed for exactly the same supercritical dynamics (with 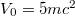 ), but
), but 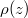 was obtained based on the (dressed) states for
was obtained based on the (dressed) states for 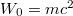 and 2mc2. As expected, all these curves match outside the force region but they differ significantly inside.
and 2mc2. As expected, all these curves match outside the force region but they differ significantly inside.
The rather monotonic trend from 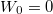 to
to  for each location z suggests that the density at
for each location z suggests that the density at 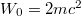 is not a singular limit and there is nothing special about the threshold to supercriticality. We can therefore exploit our knowledge of the densities for several subcritical values of W0 (used in the definition of the states) and use a quadratic extrapolation (in W0) to predict the "density" of interest for
is not a singular limit and there is nothing special about the threshold to supercriticality. We can therefore exploit our knowledge of the densities for several subcritical values of W0 (used in the definition of the states) and use a quadratic extrapolation (in W0) to predict the "density" of interest for  . The result shown by the dashed lines for the relevant case
. The result shown by the dashed lines for the relevant case 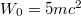 is quite remarkable in several respects. First, the rise of the electronic density close to z = 0 (observed for W0 < 5mc2) has disappeared. Second, while
is quite remarkable in several respects. First, the rise of the electronic density close to z = 0 (observed for W0 < 5mc2) has disappeared. Second, while 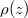 decreases in z in a similar fashion as for W0 < 5mc2, it approaches zero for
decreases in z in a similar fashion as for W0 < 5mc2, it approaches zero for 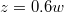 , which was identified in fig. 1 with the beginning of the no-electron production region. Quite remarkably, in this region the extrapolated ρ is even negative, which suggests that this "density" cannot be obtained as the expectation value of any positive definite Hermitian operator
, which was identified in fig. 1 with the beginning of the no-electron production region. Quite remarkably, in this region the extrapolated ρ is even negative, which suggests that this "density" cannot be obtained as the expectation value of any positive definite Hermitian operator 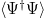 .
.
The third and fourth means to examine the interaction zone are based on the attempt to associate the long-time (energy-dependent) creation rate 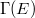 directly with the electrons' likelihood of being created at location
directly with the electrons' likelihood of being created at location 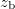 . In other words, if we assume again that the electron is born at rest with energy
. In other words, if we assume again that the electron is born at rest with energy  , its birth location for our potential is
, its birth location for our potential is 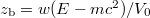 . It was suggested [12] that the energy production rate
. It was suggested [12] that the energy production rate 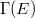 can be obtained directly from the quantum-mechanical transmission coefficient
can be obtained directly from the quantum-mechanical transmission coefficient ![$T(E)~[=2\pi\Gamma(E)]$](https://content.cld.iop.org/journals/0295-5075/116/4/40003/revision1/epl18272ieqn62.gif) for an incoming electron. In the steady state, we consistently recover the total rate as
for an incoming electron. In the steady state, we consistently recover the total rate as 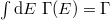 , where the energy integration range is
, where the energy integration range is 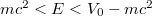 , corresponding to the limited energy range where Klein tunneling occurs and
, corresponding to the limited energy range where Klein tunneling occurs and 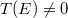 . For our potential, this leads us to conjecture a position-dependent electron creation rate as
. For our potential, this leads us to conjecture a position-dependent electron creation rate as ![$\Gamma(z)\equiv V_0T[mc^{2}+V(z)]/(2\pi w)\theta (z)\theta (z_{\mathrm{cr}}-z)$](https://content.cld.iop.org/journals/0295-5075/116/4/40003/revision1/epl18272ieqn66.gif) . Here
. Here  is the unit step function and
is the unit step function and  is the largest possible position for the creation to occur (leading to the maximal created energy
is the largest possible position for the creation to occur (leading to the maximal created energy  ). For consistency, this spatially dependent electron creation rate has to satisfy
). For consistency, this spatially dependent electron creation rate has to satisfy  .
.
Hypothetical electrons created at positions  would be accelerated by the potential to a larger energy than the one observed
would be accelerated by the potential to a larger energy than the one observed 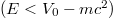 . This suggests that electrons cannot be created at
. This suggests that electrons cannot be created at 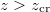 . This is again fully consistent with the findings from figs. 1 and 2. In order to have a more quantitative check, we can construct the steady-state density by superimposing all energy eigenstates
. This is again fully consistent with the findings from figs. 1 and 2. In order to have a more quantitative check, we can construct the steady-state density by superimposing all energy eigenstates 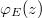 of the Hamiltonian
of the Hamiltonian ![$H=[m^{2}c^{4}+c^{2}p^{2}]^{1/2} + 5mc^{2} S(z)$](https://content.cld.iop.org/journals/0295-5075/116/4/40003/revision1/epl18272ieqn75.gif) with a weight factor given by the probability to generate this energy,
with a weight factor given by the probability to generate this energy, 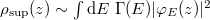 . While this superposition has some small oscillatory features that are characteristic of the energy eigenstates for a linear potential, its overall shape (crosses in fig. 2) matches the density obtained from the extrapolation very well.
. While this superposition has some small oscillatory features that are characteristic of the energy eigenstates for a linear potential, its overall shape (crosses in fig. 2) matches the density obtained from the extrapolation very well.
Next, we will argue that the steady state of the quantum field-theoretical density 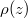 inside the supercritical barrier can even be reproduced qualitatively from a remarkable simple model of classical mechanical (relativistic) electrons that are created by the potential and then subsequently accelerated by it. To have an unambiguous test, we do not use any adjustable parameters and only assume that a particle is born at time
inside the supercritical barrier can even be reproduced qualitatively from a remarkable simple model of classical mechanical (relativistic) electrons that are created by the potential and then subsequently accelerated by it. To have an unambiguous test, we do not use any adjustable parameters and only assume that a particle is born at time 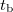 and position
and position  with the spatial creation rate
with the spatial creation rate 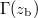 given above. For
given above. For 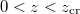 , a single particle's spatial probability to be detected at location z and time t is given by
, a single particle's spatial probability to be detected at location z and time t is given by 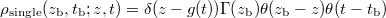 , where the relativistic trajectory is given by
, where the relativistic trajectory is given by ![$g(t)\equiv [(m^{2}c^{4}+c^{2}a^{2}t^{2})^{1/2}- mc^{2}]/a$](https://content.cld.iop.org/journals/0295-5075/116/4/40003/revision1/epl18272ieqn83.gif) with
with 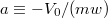 . In order to obtain the total steady-state distribution we have to integrate over all possible birth locations and birth times,
. In order to obtain the total steady-state distribution we have to integrate over all possible birth locations and birth times, 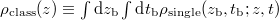 . This integral simplifies to
. This integral simplifies to ![$\rho_{\mathrm{class}}(z)\equiv\int ^{\infty}_0\text{d}t\Gamma[z-g(t)]$](https://content.cld.iop.org/journals/0295-5075/116/4/40003/revision1/epl18272ieqn86.gif) . The resulting classical density was indicated in fig. 2 by the open circles for comparison. The qualitative agreement (in the absence of any adjustable parameters) suggests that some aspects of the relativistic quantum field-theoretical pair creation process inside the interaction zone can be understood in terms of the dynamics of an ensemble of classical particles.
. The resulting classical density was indicated in fig. 2 by the open circles for comparison. The qualitative agreement (in the absence of any adjustable parameters) suggests that some aspects of the relativistic quantum field-theoretical pair creation process inside the interaction zone can be understood in terms of the dynamics of an ensemble of classical particles.
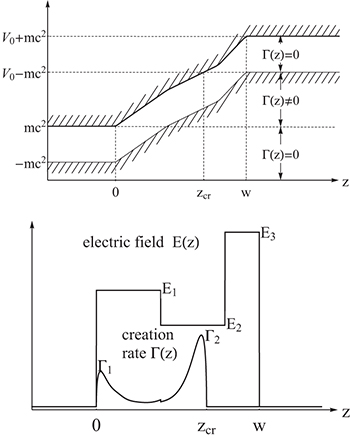
Finally, our findings allow us also to comment on the traditional tunneling picture of pair creation for the three-step form electric field shown in fig. 3. In this picture, the energy spectrum is usually visualized by up-shifting the lower-negative-energy continuum for z > w by V0, such that for the band 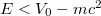 it becomes degenerate with the positive-energy continuum. This picture also visualizes the existence of the creation-free spatial domain
it becomes degenerate with the positive-energy continuum. This picture also visualizes the existence of the creation-free spatial domain 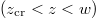 , which in this case matches the region where the electric field
, which in this case matches the region where the electric field ![$[E(z)=E_{3}]$](https://content.cld.iop.org/journals/0295-5075/116/4/40003/revision1/epl18272ieqn102.gif) is actually largest. We should also remark that a recent relativistic study by Woellert et al. [13] extended this approach to combined electric and magnetic fields.
is actually largest. We should also remark that a recent relativistic study by Woellert et al. [13] extended this approach to combined electric and magnetic fields.
Fig. 3: The usual tunneling picture for a supercritical potential V(z). The top panel compares the associated three-step electric field ![$[E(z)\sim \text{d}V/\text{d}z]$](https://content.cld.iop.org/journals/0295-5075/116/4/40003/revision1/epl18272ieqn87.gif) with the resulting spatial pair creation rate
with the resulting spatial pair creation rate 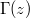 . The likelihood of electron creation
. The likelihood of electron creation 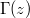 is actually largest
is actually largest 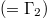 in those regions where the field is smallest
in those regions where the field is smallest 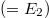 and vice versa (
and vice versa ( for
for 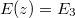 ). For
). For 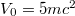 and
and 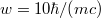 this leads to
this leads to 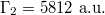 [
[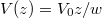 (for 0 < z < 0.4w),
(for 0 < z < 0.4w), 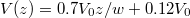 (for 0.4w < z < 0.8w) and
(for 0.4w < z < 0.8w) and 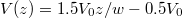 (for 0.8w < z < w)].
(for 0.8w < z < w)].
Download figure:
Standard imageIt should be clear that the true position-dependent electron creation probability 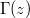 is not proportional to the electric field
is not proportional to the electric field 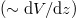 unless for the very special case of Schwinger's limit of an infinitely extended constant force region. In the more practical case of finite spatial geometries of inhomogenous supercritical electric fields E(z), other factors determine
unless for the very special case of Schwinger's limit of an infinitely extended constant force region. In the more practical case of finite spatial geometries of inhomogenous supercritical electric fields E(z), other factors determine 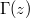 . In our simple one-dimensional example of fig. 1,
. In our simple one-dimensional example of fig. 1,  can be calculated from the quantum-mechanical transmission coefficient, which depends on the overlap between the degenerate energy continua. Its functional dependence on z is also remarkably similar to the offset
can be calculated from the quantum-mechanical transmission coefficient, which depends on the overlap between the degenerate energy continua. Its functional dependence on z is also remarkably similar to the offset 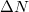 presented in the figure.
presented in the figure.
So far our discussion has been focused on the spatial probability of the electrons. The same analysis performed for the corresponding created positrons would lead to the same conclusions, as the corresponding positronic and electronic densities are just related to each other by inversion around the center of the electric field. This leads to the rather interesting conclusion that while electrons cannot be created permanently for 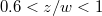 (for the electric-field configuration of figs. 1 and 2), the positron's spatial no-production region is different,
(for the electric-field configuration of figs. 1 and 2), the positron's spatial no-production region is different, 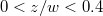 . This could suggest that the purely classical picture of two point particles having to be created at precisely the same location is not necessarily helpful in these regions.
. This could suggest that the purely classical picture of two point particles having to be created at precisely the same location is not necessarily helpful in these regions.
In summary, we have made several proposals for theoretical methods to examine the pair creation process inside the supercritical force field, which justify the introduction of a spatially dependent electron creation rate  . Especially the extrapolation-based charge densities and their direct classical mechanical analogue should provide useful theoretical tools for future studies to maximize the yield by better understanding the dynamics inside the interaction region. The methods consistently suggest that a larger local electric field does not necessarily correlate with an increase of the pair creation yield. This finding may have some implications for the experimental design of optimal laser pulse configurations that can maximize the pair creation process.
. Especially the extrapolation-based charge densities and their direct classical mechanical analogue should provide useful theoretical tools for future studies to maximize the yield by better understanding the dynamics inside the interaction region. The methods consistently suggest that a larger local electric field does not necessarily correlate with an increase of the pair creation yield. This finding may have some implications for the experimental design of optimal laser pulse configurations that can maximize the pair creation process.
Acknowledgments
QZL would like to thank ILP for the nice hospitality during his visit to Illinois State. We also truly appreciate the anonymous reviewer for extremely helpful suggestions. This work has been supported by the NSF and the NSFC (No. 11529402, 11520101003).