Exact solution of the Duffin-Kemmer-Petiau (DKP) equation in the magnetic field by considering cosmic string background in (1 + 2)-dimensions

The Duffin-Kemmer-Petiau (DKP) equation appeared more than seventy years ago and introduced a basis which enabled theoretical physicists to investigate both spin-0 and spin-1 particles on the basis of a single equation in the relativistic regime [1–4]. The DKP equation is similar to the Dirac equation, but we replace the algebra of the γ matrices by β matrices [5]. β matrices have three irreducible representations: the one-dimensional representation which is trivial, the five-dimensional representation that is for spin-0 particles and the ten-dimensional one representing spin-1 particles [6]. The DKP formalism enjoys a richness of couplings not capable of being expressed in the Klein-Gordon and Proca theories [7,8]. Till now, the equation has been used to analyze various physical phenomena and the challenge of equivalence between the DKP equation and its counterparts, i.e., Klein-Gordon (for spin-zero particles) and Proca equations is not closed [9–16]. However, the DKP equation has wide applications on different areas including meson spectroscopy, cosmology and nuclear-hadron interactions [17–19].

Cosmic strings have been considered for 30 years as a possible new form of cosmic mass energy [20–22]. Cosmic strings are topologically stable objects which might be found during a phase transition in the early universe and arise as topological defects in various gauge theories (see, e.g., [23]), or as a macroscopic variant of the fundamental strings [24]. Cosmic strings are particularly interesting since they may have played relevant cosmological roles, such as, for example, large-scale structures or galaxy formation and their detection can be an observational confirmation of the standard theory [25]. Recently, it was realised that cosmic strings could be produced in string-theory–inspired inflation scenarios [26–29] and as was mentioned in ref. [30], cosmic-string searches are generally constraining a somehow averaged value of the tension. The effects of the topological defect in the equation of motion, energy spectrum, and DKP spinor are analyzed and discussed in ref. [31].

In this paper we will focus on the behavior of the DKP equation in cosmic strings and calculate the wave function and the explicit energy spectrum.

In general, solving the DKP equation in (1 + 3)-dimensional space-time is a difficult process since it has 16 components. Another option is to study the problem in fewer dimensions. Mathematically, fewer dimensions are simpler, but can still allow us to understand the problem.

In this section, we describe the curved space-time background and the rotating frame. We choose the cosmic-string space-time background, where the line element is given by

$$\begin{equation} \text{d}s^{2}=-\text{dt}^{2}+\text{d}\rho^{2}+\eta^{2}\rho^{2}\text{d}\varphi^{2}. \end{equation} \tag{ 1 }$$

The DKP equation for bosons is given by

$$\begin{equation} \left[ {i\tilde{{\beta }}^{a}(\partial_{0} +ieA_{a} )-M)} \right]\Psi =0, \end{equation} \tag{ 2 }$$

where the tilde is used to refer to the β matrices considered in the Minkowski space-time. The β matrices here, called the Kemmer matrices, are $16 \times 16$ matrices. The matrices β satisfy the algebra

$$\begin{equation} \tilde{{\beta}}^{a}\tilde{{\beta}}^{b}\tilde{{\beta}}^{c}+\tilde{{\beta}}^{c} \tilde{{\beta}}^{b}\tilde{{\beta}}^{a}=\tilde{{\beta}}^{a}\delta^{bc} +\tilde{{\beta}}^{c}\delta^{ba} \end{equation} \tag{ 3 }$$

and obey the commutation rules introduced first by Duffin.

In (1 + 2)-dimensional curved space-time the covariant generalization of the DKP equation in the presence of external electromagnetic fields is given by

$$\begin{equation} \left[ {i\beta^{\mu }\left( {\partial_{\mu } -\Sigma_{\mu } +ieA_{\mu } } \right)-M} \right]\Psi =0, \end{equation} \tag{ 4 }$$

where M is the mass of the bosons, 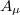$A_{\mu }$ is the 4-vector potential, e is the electrical charge and $\beta^{\mu }$ are the Kemmer matrices obtained via [32,33]

$$\begin{equation} \beta^{\mu }(x)=\gamma^{\mu }(x)\otimes I+I\otimes \gamma^{\mu }(x), \end{equation} \tag{ 5 }$$

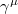where $\gamma^{\mu}$ are the Dirac matrices.

The relation to the flat Minkowski space-time is

$$\begin{equation} \beta^{\mu }(x)=e_{i}^{\mu } (x)\tilde{{\beta }}^{i}, \end{equation} \tag{ 6 }$$

where $e_{i}^{\mu } (x)$ are tetrads satisfying

$$\begin{equation} g_{\mu \upsilon } =e_{\mu }^{i} e_{\upsilon }^{j} \eta_{ij}, \qquad e_{(a)}^{\mu } e_{\mu }^{b} =\delta_{a}^{b}, \end{equation} \tag{ 7 }$$

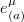where $e_{\left( a \right)}^{\mu }$ has two kinds of indices: μ labels the general space-time coordinate and $(a)$ labels the local Lorentz space-time or local laboratory coordinates.

The spinorial connections for spin-one particles given in eq. (5) are written as

$$\begin{equation} \Sigma_{\mu } =\Gamma_{\mu } \otimes I+I\otimes \Gamma_{\mu }, \end{equation} \tag{ 8 }$$

where $\Gamma_{\mu }$ are the spinorial connections for the spin-(1/2) particles and they are given by

$$\begin{equation} \Gamma_{\mu } =-\frac{1}{8}\omega_{\mu ab} [\gamma^{a},\gamma^{b}], \end{equation} \tag{ 9 }$$

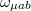where $\omega_{\mu ab}$ is the spin connection, given by

$$\begin{equation} \omega_{\mu ab} =\eta_{ac} e_{\upsilon }^{c} e_{b}^{\sigma } \Gamma _{\sigma \mu }^{\upsilon } -\eta_{ac} e_{\upsilon }^{c} \partial_{\mu } e_{b}^{\upsilon }, \end{equation} \tag{ 10 }$$

where $\Gamma_{\upsilon \lambda }^{\alpha }$ are the Christoffel symbols given by

$$\begin{equation*} \Gamma_{\upsilon \lambda }^{\alpha } =\frac{1}{2}g^{\alpha \beta }\partial _{\lambda } g_{\beta \upsilon } +\partial_{\upsilon } g_{\beta \lambda } +\partial_{\beta } g_{\lambda \upsilon}. \end{equation*}$$

The DKP equation for a general (1 + 2)-dimensional metric given by eq. (2) can be written as follows:

$$\begin{eqnarray} & \left[\vphantom{\frac{1}{\eta \rho }} {\beta^{0}\left( {\partial_{0} -\Sigma_{0} +ieA_{0} } \right)+\beta^{1}\left( {\partial_{1} -\Sigma_{1} +ieA_{1} } \right)} \right.\nonumber \\ & +\left. \frac{1}{\eta \rho }\beta^{2}\left( {\partial_{2} -\Sigma_{2} +ieA_{2}} \right)+Mi \right]\Psi =0. \end{eqnarray} \tag{ 11 }$$

With eq. (5) the DKP equation changes to

$$\begin{eqnarray} &\, \left[\vphantom{\frac{1}{\eta \rho }} {\left( {\gamma^{0}\otimes I+I\otimes \gamma^{0}} \right)\left( {\partial_{0} -\Sigma_{0} +ieA_{0} } \right)} \right.\nonumber \\ & \left.+\left( {\gamma^{1}\otimes I+I\otimes \gamma^{1}} \right)\left( {\partial _{1} -\Sigma_{1} +ieA_{1} } \right)+\frac{1}{\eta \rho }\right. \nonumber\\ & \times\left. {\left( {\gamma^{2}\otimes I+I\otimes \gamma^{2}} \right)\left( {\partial_{2} -\Sigma_{2} +ieA_{2} } \right)+Mi} \vphantom{\frac{1}{\eta \rho }}\right]\Psi =0. \end{eqnarray} \tag{ 12 }$$

By multiplying this equation on $\left( {\gamma^{0}\otimes I+I\otimes \gamma^{0}} \right)$ we have

$$\begin{eqnarray} &\, \left[\vphantom{\frac{1}{\eta \rho }} \left( {\gamma^{0}\otimes I+I\otimes \gamma^{0}} \right)\left( {\partial_{0} -\Sigma_{0} +ieA_{0} } \right)+\big( {\gamma^{0}\gamma ^{1}\otimes \gamma^{0}} \right.\nonumber\\ & +\left. {\gamma^{0}\otimes \gamma^{0}\gamma^{1}} \big)\left( {\partial _{1} -\Sigma_{1} +ieA_{1} } \right)+\frac{1}{\eta \rho }\right. \nonumber\\ & \left.\times\left( {\gamma^{0}\gamma^{2}\otimes \gamma^{0}+\gamma^{0}\otimes \gamma ^{0}\gamma^{2}} \right)\left( {\partial_{2} -\Sigma_{2} +ieA_{2} } \right) \right.\nonumber\\ &\left. +{Mi\left( {\gamma^{0}\otimes I+I\otimes \gamma^{0}} \right)} \vphantom{\frac{1}{\eta \rho }}\right]\Psi =0. \end{eqnarray} \tag{ 13 }$$

We choose the space-time–independent Dirac matrices in terms of Pauli matrices as

$$\begin{equation} \gamma^{0}=\left( {{\begin{array}{rr} 1 &\quad 0 \\ 0 &\quad {-1} \\ \end{array} }} \right), \qquad \gamma^{i}=\left( {{\begin{array}{rr} 0 &\quad {\sigma_{i} } \\ {-\sigma_{i} } &\quad 0 \\ \end{array} }} \right). \end{equation} \tag{ 14 }$$

Now we define $\alpha^{1}=\gamma^{0}\gamma^{1}$ and calculating this parameter shows that

$$\begin{equation} \alpha^{i}=\left( {{\begin{array}{*{20}c} 0 &\quad {\sigma_{i} }\\ {\sigma_{i} } &\quad 0 \\ \end{array} }} \right). \end{equation} \tag{ 15 }$$

Spinorial connections for the relevant background are found to be

$$\begin{equation} \Sigma_{0} =\Sigma_{1} =0 \end{equation} \tag{ 16 }$$

and

$$\begin{equation} \Sigma_{2} =-\frac{1}{2}\left( {1-\eta } \right)\left( {{\begin{array}{*{20}c} 0 & {\sigma_{2} } & {\sigma_{2} } & 0 \\ {\begin{array}{l} \sigma_{2} \\ \sigma_{2} \\ \end{array}} & {\begin{array}{l} 0 \\ 0 \\ \end{array}} & {\begin{array}{l} 0 \\ 0 \\ \end{array}} & {\begin{array}{l} \sigma_{2} \\ \sigma_{2} \\ \end{array}} \\ 0 & {\sigma_{2} } & {\sigma_{2} } & 0 \\ \end{array} }} \right). \end{equation} \tag{ 17 }$$

The Kemmer wave function $\Psi_{K}$ is now a 4-component and it is written as the symmetric direct product of two Dirac wave functions as

$$\begin{eqnarray*} &&\Psi_{K} =\Psi_{D} \otimes \Psi_{D} =\left( {\begin{array}{l} \eta \\ \varphi \\ \end{array}} \right)\otimes \left( {\begin{array}{l} \eta \\ \varphi \\ \end{array}} \right)=\left( {\begin{array}{l} \eta \eta \\ \eta \varphi \\ \varphi \eta \\ \varphi \varphi \\ \end{array}} \right)=\left( {\begin{array}{l} \Psi_{1} \\ \Psi_{2} \\ \Psi_{3} \\ \Psi_{4} \\ \end{array}} \right). \end{eqnarray*}$$

We introduce the wave function as [34]

$$\begin{equation} \Psi =\left( {\Psi_{1},\Psi_{2},\Psi_{3},\Psi_{4} } \right)^{T}. \end{equation} \tag{ 18 }$$

In this model, a spin-1 particle is considered as a particle system of two spin-(1/2) particles with equal mass, instead of a single spin-1 particle.

By replacing eqs. (14), (17) and (18) in eq. (13) we have

$$\begin{eqnarray} &\begin{array}{ll} &\left\{\!\!\left(\! {{\begin{array}{*{20}c} 2 & 0 & 0 & 0 \\ {\begin{array}{l} 0 \\ 0 \\ \end{array}} & {\begin{array}{c} 0 \\ 0 \\ \end{array}} & {\begin{array}{c} 0 \\ 0 \\ \end{array}} & {\begin{array}{c} 0 \\ 0 \\ \end{array}} \\ 0 & 0 & 0 & {-2} \\ \end{array} }} \!\right)\left( {\partial_{0} +ieA_{0} } \right)\!+\!\left(\! {{\begin{array}{*{20}c} 0 & {\sigma_{1} } & {\sigma_{1} } & 0 \\ {\begin{array}{l} \sigma_{1} \\ \sigma_{1} \\ \end{array}} & {\begin{array}{c} 0 \\ 0 \\ \end{array}} & {\begin{array}{c} 0 \\ 0 \\ \end{array}} & {\begin{array}{c} -\sigma_{1} \\ -\sigma_{1} \\ \end{array}} \\ 0 & {-\sigma_{1} } & {-\sigma_{1} } & 0 \\ \end{array} }}\!\!\! \right) \right. \\ &\left.\cdot\left( {\partial_{1} +ieA_{1} } \right)+\dfrac{1}{\eta \rho }\left( {{\begin{array}{*{20}c} 0 & {\sigma_{2} } & {\sigma_{2} } & 0 \\ {\begin{array}{l} \sigma_{2} \\ \sigma_{2} \\ \end{array}} & {\begin{array}{c} 0 \\ 0 \\ \end{array}} & {\begin{array}{c} 0 \\ 0 \\ \end{array}} & {\begin{array}{c} -\sigma_{2} \\ -\sigma_{2} \\ \end{array}} \\ 0 & {-\sigma_{2} } & {-\sigma_{2} } & 0 \\ \end{array} }} \right)\right.\\ \end{array} \nonumber\\ &\begin{array}{l} \left.\,\,\,\times\left( {\partial_{2} +\dfrac{1-\eta }{2}\left( {{\begin{array}{*{20}c} 0 & {\sigma_{2} } & {\sigma_{2} } & 0 \\ {\begin{array}{l} \sigma_{2} \\ \sigma_{2} \\ \end{array}} & {\begin{array}{c} 0 \\ 0 \\ \end{array}} & {\begin{array}{c} 0 \\ 0 \\ \end{array}} & {\begin{array}{c} \sigma_{2} \\ \sigma_{2} \\ \end{array}} \\ 0 & {\sigma_{2} } & {\sigma_{2} } & 0 \\ \end{array} }} \right)+ieA_{2} } \right)\right.\end{array} \nonumber \\ &\begin{array}{l} \,\,\,+\left. \,\,Mi\left( {{\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ {\begin{array}{l} 0 \\ 0 \\ \end{array}} & {\begin{array}{c} -1 \\ 0 \\ \end{array}} & {\begin{array}{c} 0 \\ -1 \\ \end{array}} & {\begin{array}{c} 0 \\ 0 \\ \end{array}} \\ 0 & 0 & 0 & 1 \\ \end{array} }} \right) \right\} \left( \begin{array}{l} \Psi_{1} \\ \Psi_{2} \\ \Psi_{3} \\ \Psi_{4} \\ \end{array} \right)=0. \end{array} \end{eqnarray} \tag{ 19 }$$

We obtain four first-order differential equations:

$$\begin{eqnarray} &\, (2\partial_{0} +ieA_{0} +Mi)\Psi_{1} +\left[ {\sigma_{1} \left( {\partial_{1} +ieA_{1} } \right)+\frac{\sigma_{2} }{\eta \rho }} \right. \nonumber\\ & \cdot\left. \left(\partial_{2} +\frac{1-\eta }{2}\sigma_{2} +ieA_{2} \right)\right]\left(\Psi_{2} +\Psi_{3} \right)=0, \end{eqnarray} \tag{ 20 }$$

$$\begin{eqnarray} &\, \left[ {\sigma_{1} \left( {\partial_{1} +ieA_{1} } \right)+\frac{\sigma _{2} }{\eta \rho }\left( {\partial_{2} +\frac{1-\eta }{2}\sigma_{2} +ieA_{2} } \right)} \right] \nonumber\\ & \times\left( {\Psi_{1} -\Psi_{4} } \right)-Mi\Psi_{2} =0, \end{eqnarray} \tag{ 21 }$$

$$\begin{eqnarray} &\, \left[ {\sigma_{1} \left( {\partial_{1} +ieA_{1} } \right)+\frac{\sigma _{2} }{\eta \rho }\left( {\partial_{2} +\frac{1-\eta }{2}\sigma_{2} +ieA_{2} } \right)} \right]\nonumber\\ & \times\left( {\Psi_{1} -\Psi_{4} } \right)-Mi\Psi_{3} =0, \end{eqnarray} \tag{ 22 }$$

$$\begin{eqnarray} &\, (-2\partial_{0} +ieA_{0} +Mi)\Psi_{4} -\left[ {\sigma_{1} \left( {\partial_{1} +ieA_{1} } \right)} \right. \nonumber\\ & +\left. {\frac{\sigma_{2} }{\eta \rho }\left( {\partial_{2} +\frac{1-\eta }{2}\sigma_{2} +ieA_{2} } \right)} \right]\left( {\Psi_{2} +\Psi_{3} } \right)=0.\quad \end{eqnarray} \tag{ 23 }$$

From eqs. (21) and (23) we obtain

$$\begin{equation} \Psi_{2} =\Psi_{3}. \end{equation} \tag{ 24 }$$

It is easy to find the other components of the wave function from the differential relations given above. For this purpose, by replacing eq. (24) into eqs. (20) and (23), we have

$$\begin{eqnarray} \Psi_{1} &= \frac{-2\left[ {\sigma_{1} \left( {\partial_{1} +ieA_{1} } \right)+\frac{\sigma_{2} }{\eta \rho }\left( {\partial_{2} +\frac{1-\eta }{2}\sigma_{2} +ieA_{2} } \right)} \right]}{(2\partial_{0} +ieA_{0} +Mi)}\Psi_{2}, \nonumber\\ \end{eqnarray} \tag{ 25 }$$

$$\begin{eqnarray} \Psi_{4} &= \frac{2\left[ {\sigma_{1} \left( {\partial_{1} +ieA_{1} } \right)+\frac{\sigma_{2} }{\eta \rho }\left( {\partial_{2} +\frac{1-\eta }{2}\sigma_{2} +ieA_{2} } \right)} \right]}{(-2\partial_{0} +ieA_{0} +Mi)}\Psi_{2}. \nonumber\\ \end{eqnarray} \tag{ 26 }$$

Now by replacing eqs. (24), (25) and (26) in eq. (21) we have one differential equation,

$$\begin{eqnarray} &\, \left\{\left( {-2} \right)\left[ {\sigma_{1} \left( {\partial_{1} +ieA_{1} } \right)+\frac{\sigma_{2} }{\eta \rho }\left( {\partial_{2} +\frac{1-\eta }{2}\sigma_{2} +ieA_{2} } \right)} \right]^{2} \right.\nonumber \\ & \left. -\frac{Mi\left( {\left( {ieA_{0} +Mi} \right)^{2}-4\partial _{0}^{2} } \right)}{2\left( {ieA_{0} +Mi} \right)} \right\} \Psi_{2} =0. \end{eqnarray} \tag{ 27 }$$

In eq. (27) if we consider $ieA_{0} =0$, $ieA_{1} =a_{1} \rho +\frac{b_{1} }{\rho }$, $ieA_{2} =a_{2} \rho +\frac{b_{2} }{\rho }$, we have

$$\begin{eqnarray} &\, \left\{ -\partial_{0}^{2} -\left( {\frac{M}{2}} \right)^{2}+\left[ {\sigma_{1} \left( {\partial_{1} +a_{1} \rho +\frac{b_{1} }{\rho }} \right)+} \right.\frac{\sigma_{2} }{\eta \rho } \right.\nonumber \\ &.\left. \left. {\left( {\partial_{2} +\frac{1-\eta }{2}\sigma_{2} +a_{2} \rho +\frac{b_{2} }{\rho }} \right)} \right]^{2} \right\} \Psi_{2} =0. \end{eqnarray} \tag{ 28 }$$

We consider the wave function is of the form of 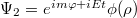$\Psi_{2} =e^{im\varphi +iEt}\phi (\rho)$, so we obtained

$$\begin{eqnarray} &\, \hspace{-0.5pc}\left\{\! \partial_{\rho }^{2} \!+\!\left[a_{1} \rho +a_{2} \rho \!+\!\frac{b_{1} }{\rho }\!+\!\frac{\sigma_{\rho } \sigma_{\varphi } im}{\eta \rho }\!+\!\frac{\sigma_{\rho } }{\eta \rho }\frac{\left( {1\!-\!\eta } \right)}{2}+\frac{\sigma_{\varphi } \sigma_{\rho } im}{\eta \rho } \right. \right. \nonumber\\ & \hspace{-0.5pc}\left. +\frac{\sigma_{\varphi } \sigma_{\rho } }{\eta \rho }\frac{\left( {1-\eta } \right)}{2}\sigma_{\varphi } +\frac{b_{2} }{\rho } \right]\partial_{\rho } +E^{2}-\left( {\frac{M}{2}} \right)^{2}+a_{1} +2a_{1} b_{1} \nonumber\\ & \hspace{-0.5pc}+\frac{\sigma_{\rho } \sigma_{\varphi } ima_{1} }{\eta }+\frac{\sigma _{\varphi } \sigma_{\rho } ima_{2} }{\eta }+\frac{\sigma_{\varphi } \sigma _{\rho } }{\eta }\frac{\left( {1-\eta } \right)}{2}\sigma_{\varphi } a_{1} \nonumber\\ & \hspace{-0.5pc}+\frac{a_{2}^{2} }{\eta^{2}}+\left( {\frac{\sigma_{\rho } \sigma _{\varphi } a_{1} a_{2} }{\eta }+\frac{\sigma_{\varphi } \sigma_{\rho } a_{1} a_{2} }{\eta }} \right)\rho +a_{1}^{2} \rho^{2}\nonumber \\ & \hspace{-0.5pc}+\left( {\frac{\sigma_{\rho } \sigma_{\varphi } a_{2} }{\eta }+\frac{\sigma_{\rho } \sigma_{\varphi } a_{1} b_{2} }{\eta }+\frac{\sigma _{\rho } \sigma_{\varphi } b_{1} a_{2} }{\eta }+\frac{\sigma_{\varphi } \sigma_{\rho } b_{1} a_{2} }{\eta }} \right. \nonumber\\ & \hspace{-0.5pc}\left. +\frac{\sigma_{\varphi } \sigma_{\rho } b_{2} a_{1} }{\eta }+\frac{2ima_{2} }{\eta^{2}}+\frac{2\sigma_{\varphi } a_{2} }{\eta ^{2}}\frac{\left( {1-\eta } \right)}{2} \right)\frac{1}{\rho }\nonumber \\ & \hspace{-0.5pc}+\left( b_{1}^{2} -b_{1} +\frac{\sigma_{\rho } \sigma_{\varphi } b_{1} im}{\eta }+\frac{\sigma_{\rho } b_{1} }{\eta }\frac{\left( {1-\eta } \right)}{2}+\frac{\sigma_{\varphi } \sigma_{\rho } b_{1} im}{\eta } \right. \nonumber\\ & \hspace{-0.5pc}+\left. \frac{\sigma_{\varphi } \sigma_{\rho } \sigma_{\varphi } b_{1} }{\eta }\frac{\left( {1-\eta } \right)}{2}-\frac{m^{2}}{\eta ^{2}}+\frac{2im\sigma_{\varphi } }{\eta^{2}}\frac{\left( {1-\eta } \right)}{2}\right. \nonumber\\ & \hspace{-0.5pc}\left.+\frac{\left( {1-\eta } \right)^{2}}{4\eta^{2}}+\frac{2a_{2} b_{2} }{\eta^{2}} \right)\frac{1}{\rho^{2}}\nonumber \\ & \hspace{-0.5pc}+\left( {-\frac{\sigma_{\rho } \sigma_{\varphi } b_{2} }{\eta }+\frac{\sigma_{\varphi } \sigma_{\rho } b_{1} b_{2} }{\eta }+\frac{\sigma _{\rho } \sigma_{\varphi } b_{1} b_{2} }{\eta }+\frac{imb_{2} }{\eta^{2}}} \right. \nonumber\\ & \hspace{-0.6pc}\left. \left. +\frac{\left( {1-\eta } \right)}{2}\frac{2\sigma_{\varphi} b_{2} }{\eta^{2}} \!\right)\frac{1}{\rho^{3}}+\frac{b_{2}^{2} }{\eta ^{2}}\frac{1}{\rho^{4}} \!\right\} \phi (\rho )\!=\!0. \!\!\!\!\!\!\!\! \end{eqnarray} \tag{ 29 }$$

Now we define

$$\begin{eqnarray} \alpha &= a_{1} +a_{2}, \end{eqnarray} \tag{ 30 }$$

$$\begin{eqnarray} \beta &= b_{1} +b_{2} +\frac{\sigma_{\rho } \sigma_{\varphi } im}{\eta }+\frac{\sigma_{\rho } }{\eta }\frac{\left( {1-\eta } \right)}{2}, \nonumber\\ &\quad +\frac{\sigma_{\varphi } \sigma_{\rho } im}{\eta }+\frac{\sigma_{\varphi} \sigma_{\rho } }{\eta }\frac{\left( {1-\eta } \right)}{2}\sigma_{\varphi}. \end{eqnarray} \tag{ 31 }$$

And the consideration of

$$\begin{equation} \phi (\rho )=\text{e}^{-\frac{\alpha }{4}\rho^{2}-\frac{\beta }{2}\ln \rho }u \end{equation} \tag{ 32 }$$

leads to

$$\begin{eqnarray} &\, \hspace{-0.5pc}\left\{\frac{\text{d}}{\text{d}\rho^{2}}+E^{2}-\left( {\frac{M}{2}} \right)^{2}+a_{1} +2a_{1} b_{1} +\frac{\sigma_{\rho } \sigma_{\varphi } ima_{1} }{\eta } \right.\nonumber \\ & \hspace{-0.5pc}\left.+\frac{\sigma_{\varphi } \sigma_{\rho } ima_{2} }{\eta }+\frac{\sigma _{\varphi } \sigma_{\rho } }{\eta }\frac{\left( {1-\eta } \right)}{2}\sigma _{\varphi } a_{1} +\frac{a_{2}^{2} }{\eta^{2}}+\frac{\alpha \beta}{2}-\frac{\alpha }{2}+\alpha \beta \right.\nonumber\\ & \hspace{-0.5pc}\left.+\left( {\frac{\sigma_{\rho } \sigma_{\varphi } a_{1} a_{2} }{\eta }+\frac{\sigma_{\varphi } \sigma_{\rho } a_{1} a_{2} }{\eta }} \right)\rho +\left( {a_{1}^{2} +\frac{\alpha^{2}}{4}-\frac{\alpha^{2}}{2}} \right)\rho ^{2}\right. \nonumber\\ & \hspace{-0.5pc}\left.+\left( {\frac{\sigma_{\rho } \sigma_{\varphi } a_{2} }{\eta }+\frac{\sigma_{\rho } \sigma_{\varphi } a_{1} b_{2} }{\eta }+\frac{\sigma _{\rho } \sigma_{\varphi } b_{1} a_{2} }{\eta }+\frac{\sigma_{\varphi } \sigma_{\rho } b_{1} a_{2} }{\eta }} \right.\right. \nonumber\\ & \hspace{-0.5pc}\left.\left. +\frac{\sigma_{\varphi } \sigma_{\rho } b_{2} a_{1} }{\eta} +\frac{2ima_{2} }{\eta^{2}}+\frac{\sigma_{\varphi } a_{2} \left( {1-\eta } \right)}{\eta^{2}} \right)\frac{1}{\rho }\right. \nonumber\\ & \hspace{-0.5pc}\left.+\left( b_{1}^{2} -b_{1} +\frac{\sigma_{\rho } \sigma_{\varphi } +\sigma _{\varphi } \sigma_{\rho }}{\eta }b_{1} im\right.\right.\nonumber\\ & \hspace{-0.5pc}\left.\left.+\frac{\sigma_{\rho } b_{1} \left( {1-\eta } \right)+\sigma_{\varphi } \sigma_{\rho } \sigma_{\varphi} b_{1} \left( {1-\eta } \right)}{2\eta}-\frac{m^{2}}{\eta^{2}} \right. \right.\nonumber\\ & \hspace{-0.5pc}\left.\left. +\frac{im\sigma_{\varphi } \left( {1-\eta} \right)}{\eta^{2}}+\frac{\left( {1-\eta } \right)^{2}}{4\eta ^{2}}+\frac{2a_{2} b_{2} }{\eta^{2}}+\frac{3\beta^{2}}{4}+\frac{\beta }{2} \right)\frac{1}{\rho^{2}}\right.\nonumber\\ & \hspace{-0.5pc}+\left.\left( {-\frac{\sigma_{\rho } \sigma_{\varphi } b_{2} }{\eta} +\frac{\sigma_{\varphi } \sigma_{\rho } b_{1} b_{2} }{\eta }+\frac{\sigma_{\rho } \sigma_{\varphi } b_{1} b_{2} }{\eta }+\frac{imb_{2} }{\eta^{2}}} \right.\right. \nonumber\\ & \hspace{-0.5pc}\left. \left. +\frac{\sigma_{\varphi } b_{2} \left( {1-\eta } \right)}{\eta^{2}} \right)\frac{1}{\rho^{3}}+\frac{b_{2}^{2} }{\eta ^{2}}\frac{1}{\rho^{4}} \right\}u=0. \end{eqnarray} \tag{ 33 }$$

In order to solve the above differential equation, let us assume, for the wave function [35],

$$\begin{equation} u=\exp \left( g(\rho ) \right). \end{equation} \tag{ 34 }$$

Now, for the function 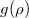$g(\rho )$, we make use of the following ansatz:

$$\begin{equation} g(\rho )=\text{c}_{1} \rho^{2}+\text{c}_{2} \rho +\text{c}_{3} \ln \rho +\frac{\text{c}_{4} }{\rho }. \end{equation} \tag{ 35 }$$

By substitution of 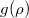$g(\rho )$ into eq. (33) and then taking the first- and second-order derivative of the obtained equation, we get

$$\begin{equation} {u}''=\left[ {{g}''(T)+{g}'^{2}(T)} \right]u. \end{equation} \tag{ 36 }$$

We therefore have

$$\begin{eqnarray} & {g}'^{2}(\rho )+{g}''(\rho )=2\text{c}_{1} +\text{c}_{2}^{2} +4\text{c}_{1} \text{c}_{3} +4\text{c}_{1} \text{c}_{2} \rho +\text{4c}_{1}^{2} \rho^{2} \nonumber\\ & ~~+\left( {2\text{c}_{2} \text{c}_{3} -4\text{c}_{1} \text{c}_{4} } \right)\frac{1}{\rho }+\left( {\text{c}_{3}^{2} -\text{c}_{3} -2\text{c}_{2} \text{c}_{4} } \right)\frac{1}{\rho^{2}}\nonumber\\ & ~~+\left( {\text{2c}_{4} -2\text{c}_{3} \text{c}_{4} } \right)\frac{1}{\rho^{3}}+\text{c}_{4}^{2} \frac{1}{\rho^{4}}. \end{eqnarray} \tag{ 37 }$$

By comparing eq. (37) with eq. (33) it can be found that

$$\begin{eqnarray} &\, \text{2c}_{1} +\text{c}_{2}^{2} +4\text{c}_{1} \text{c}_{3} =E^{2}-\left( \frac{M}{2} \right)^{2}+a_{1} +2a_{1} b_{1} +\alpha \beta \nonumber \\ & +\frac{\alpha \beta -\alpha }{2}+\frac{\sigma_{\rho } \sigma_{\varphi } a_{1} +\sigma_{\varphi } \sigma_{\rho } a_{2} }{\eta }im\nonumber\\ & +\frac{\sigma _{\varphi } \sigma_{\rho } \sigma_{\varphi } a_{1} }{\eta }\frac{\left( {1-\eta } \right)}{2}+\frac{a_{2}^{2} }{\eta^{2}}, \end{eqnarray} \tag{ 38 }$$

$$\begin{eqnarray} & 4\text{c}_{1} \text{c}_{2} =\frac{\sigma_{\rho } \sigma_{\varphi } +\sigma _{\varphi } \sigma_{\rho } }{\eta }a_{1} a_{2}, \end{eqnarray} \tag{ 39 }$$

$$\begin{eqnarray} & \text{4c}_{1}^{2} =a_{1}^{2} +\frac{\alpha^{2}}{4}-\frac{\alpha^{2}}{2}, \end{eqnarray} \tag{ 40 }$$

$$\begin{eqnarray} &\, 2\text{c}_{2} \text{c}_{3} -4\text{c}_{1} \text{c}_{4} =\frac{\sigma_{\rho } \sigma_{\varphi } a_{2} }{\eta }+\frac{\sigma_{\rho } \sigma_{\varphi } +\sigma_{\varphi } \sigma_{\rho } }{\eta }a_{1} b_{2}\nonumber \\ & +\frac{\sigma_{\rho } \sigma_{\varphi } +\sigma_{\varphi } \sigma_{\rho}} {\eta }b_{1} a_{2} +\frac{2ima_{2} }{\eta^{2}}+\frac{\sigma_{\varphi } a_{2} }{\eta^{2}}\left( {1-\eta } \right), \\ \end{eqnarray} \tag{ 41 }$$

$$\begin{eqnarray} &\, \text{c}_{3}^{2} -\text{c}_{3} \text{-2c}_{2} \text{c}_{4} =b_{1}^{2} -b_{1} +\frac{\sigma_{\rho } \sigma_{\varphi } b_{1} im}{\eta }+\frac{\sigma_{\rho } b_{1} }{\eta }\frac{\left( {1-\eta } \right)}{2}\nonumber \\ & +\frac{\sigma_{\varphi } \sigma_{\rho } b_{1} im}{\eta }+\frac{\sigma _{\varphi } \sigma_{\rho } \sigma_{\varphi } b_{1} }{\eta }\frac{\left( {1-\eta } \right)}{2}-\frac{m^{2}}{\eta^{2}}+\frac{im\sigma_{\varphi } }{\eta^{2}}\left( {1-\eta } \right) \nonumber\\ & +\frac{\left( {1-\eta } \right)^{2}}{4\eta^{2}}+\frac{2a_{2} b_{2} }{\eta ^{2}}+\frac{3\beta^{2}}{4}+\frac{\beta }{2}, \end{eqnarray} \tag{ 42 }$$

$$\begin{eqnarray} &\, \text{2c}_{4} -2\text{c}_{3} \text{c}_{4} =-\frac{\sigma_{\rho } \sigma _{\varphi } b_{2} }{\eta }+\frac{\sigma_{\varphi } \sigma_{\rho } b_{1} b_{2} }{\eta } \nonumber\\ & +\frac{\sigma_{\rho } \sigma_{\varphi } b_{1} b_{2} }{\eta }+\frac{imb_{2} }{\eta^{2}}+\frac{\sigma_{\varphi } b_{2} \left( {1-\eta } \right)}{\eta^{2}}, \\ \end{eqnarray} \tag{ 43 }$$

$$\begin{eqnarray} & \text{c}_{4}^{2} =\frac{b_{2}^{2} }{\eta^{2}}. \end{eqnarray} \tag{ 44 }$$

Based on eq. (38) the energy spectrum was investigated and from eqs. (39)–(44) we can calculate the variable of eq. (35) and we obtain the wave function.

After applying some appropriate transformations and introducing an elegant ansatz, we have obtained exact solution to the DKP equation under the cosmic string background with the presence of magnetic field in (1+2)-dimensional space-time. We have reported the energy spectrum and wave function. These results will be useful in various branches of physics, such as theoretical nuclear physics, meson spectroscopy and cosmology. In particular, it is important to consider this equation in the expanding universe, which has considerable importance in astrophysics and cosmology. This equation may be considered insignificant at the atomic scale, where gravitational effects are weak, but the physics governing these particles plays an important role in astrophysics and cosmology, in which gravitational effects play a dominant role. In addition, studying single-particle states is important for constructing a unified theory of gravitation and quantum mechanics.

We wish to give our sincere gratitude to the referee for his technical comments.