Abstract
We investigate the metal-insulator Mott transition in a generalized version of the periodic Anderson model, in which a band of itinerant non-interacting electrons is hybridrized with a narrow and strongly correlated band. Using the dynamical mean-field theory, we show that the precondition for the Mott transition is that the total filling of the two bands takes an odd integer value. Unlike the conventional portrait of the Mott transition, this condition corresponds to a non-integer filling of the correlated band. For an integer constant occupation of the correlated orbitals the system remains a correlated metal at arbitrary large interaction strength. We picture the transition at a non-integer filling of the correlated orbital as the Mott localization of the singlet states between itinerant and strongly interacting electrons, having occupation of one per lattice site. We show that the Mott transition is of the first order and we characterize the nature of the resulting insulating state with respect to relevant physical parameters, such as the charge-transfer energy.
Export citation and abstract BibTeX RIS
Introduction
Mott localization induced by strong repulsive interaction is intrinsically a physics of commensuration. A paradigmatic example is the Mott-Hubbard transition in the Hubbard model which, in the absence of symmetry breaking, only takes place if the number of correlated electrons equals the number of lattice sites for a single-orbital model [1–4], or an integer multiple of it in the multi-orbital case [5–8]. A metal-insulator transition (MIT) occurs as the local repulsion reaches a critical value of the order of the bandwidth, when it becomes energetically convenient for the interacting electrons to localize at any lattice site. The energy gain associated to the electronic motion becomes smaller than the cost associated to charge fluctuations. Hence, the commensurability of the electron density 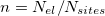 naturally emerges as a necessary condition to obtain a Mott insulator. Intuitively this commensuration implies the absence of spare sites where an electron can hop without paying extra electrostatic energy.
naturally emerges as a necessary condition to obtain a Mott insulator. Intuitively this commensuration implies the absence of spare sites where an electron can hop without paying extra electrostatic energy.
This idealized picture of the MIT in terms of integer occupied correlated orbitals becomes less clear for more realistic systems, made accessible by recently developed ab initio based methods for correlated materials. In such systems the correlated electrons in valence orbitals often hybridize with nearly uncorrelated ligand orbitals, generically reducing the occupation of the correlated bands to a non-integer value and promoting an active role of the ligand bands in determining the physics of the system. This is the case for many different transition-metal oxides (TMO) or the iron pnictides/chalcogenides [9–12], where the transition-metal d-orbitals are intertwined with p-orbitals of the oxygen or pnictogen/chalcogen atoms. Investigations of these systems have suggested that a crucial control parameter to determine the degree of correlation is the occupation of the correlated d-orbitals [13–19], which, however, does not generally correspond to an integer total number of electrons per site. This puts a challenge on the mechanism leading to the MIT in compounds with partially filled correlated orbitals. Theoretical investigation of simplified models displays seemingly contradictory results. The presence of a hybridization between the correlated and the ligand orbitals was shown to forbid the MIT in a regime of commensurate fillings of the two bands [20]. However, a Mott insulating state was found to exist for different physical regimes violating the commensurate condition on the correlated band [21–24]. These results motivate us to investigate the physical conditions which allow for a MIT once the role of the ligand bands is taken into account. In doing so, we can reconcile the physics of commensuration with the generic existence of a Mott state in more realistic systems.
This rich spectrum of results leaves many questions open about the very presence of the Mott transition in systems of this kind, and about the nature of the carriers which localize, i.e., if the ligand p-orbitals, notwithstanding their non-interacting nature, play an active role in the Mott localization, or they are mainly spectators of the d-electron localization.
In this work we provide an answer to some of these questions. We study the conditions under which a Mott transition takes place, and what its properties are in a simple, yet generic, model which captures the essential ingredients of the collective behavior of strongly correlated d-electrons hybridized with a band of non-correlated electrons. We solve the model using dynamical mean-field theory (DMFT) [25,26], a powerful and reliable non-perturbative method which has been widely used to address the Mott-Hubbard transition in a variety of models and realistic systems [8]. Our key result is to show that a zero-temperature Mott transition can occur for a partially filled correlated band, corresponding to an odd integer total number of electrons, including also those occupying the non-correlated ligand orbitals. We show that, unlike the conventional expectations, this transition does not correspond to the direct localization of correlated electrons only, but rather to that of singlets states between the two orbitals with a density of one per lattice site. Finally, we characterize the nature of the correlated insulating state with respect to experimentally relevant parameters of the system. We show that the mentioned past literature connects in this perspective and fits well in the Zaanen-Sawatzky-Allen (ZSA) diagram [27].
Model
The starting point of our analysis is a generalized version of the periodic Anderson model [22,23,28–33]. The model Hamiltonian reads

where
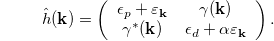
For the sake of definiteness we consider a two-dimensional system on a square lattice. The spinor  collects the operators
collects the operators  ,
,  respectively annihilating electrons with spin
respectively annihilating electrons with spin  in the wide band with dispersion
in the wide band with dispersion ![$\varepsilon_\textbf{k}=-2t_{pp}[\cos(k_x)+\cos(k_y)]$](https://content.cld.iop.org/journals/0295-5075/118/1/17004/revision1/epl18531ieqn6.gif) centered at
centered at  , and in the narrow correlated band of dispersion
, and in the narrow correlated band of dispersion ![$\alpha\varepsilon_\textbf{k}\ (\alpha\in[0,1])$](https://content.cld.iop.org/journals/0295-5075/118/1/17004/revision1/epl18531ieqn8.gif) centered at
centered at 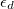 . For the sake of simplicity we assume identical dispersions in both orbitals. Qualitatively similar results can however be obtained with other, possibly more realistic, choices. The two orbitals hybridize with an amplitude
. For the sake of simplicity we assume identical dispersions in both orbitals. Qualitatively similar results can however be obtained with other, possibly more realistic, choices. The two orbitals hybridize with an amplitude 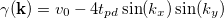 . The second term in (1) describes the local repulsion experienced by the d-electrons. In the following we set the energy unit to the conduction electrons half-bandwidth
. The second term in (1) describes the local repulsion experienced by the d-electrons. In the following we set the energy unit to the conduction electrons half-bandwidth  . We introduce the bare charge-transfer energy
. We introduce the bare charge-transfer energy  . We focus on the case
. We focus on the case 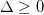 as similar results hold for the
as similar results hold for the  case. Without loss of generality we fix the zero of the energy to
case. Without loss of generality we fix the zero of the energy to  . We adjust the total density
. We adjust the total density 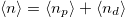 (where
(where 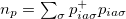 and
and 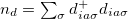 are the local number operators) by tuning the chemical potential μ. We consider the zero-temperature regime T = 0.
are the local number operators) by tuning the chemical potential μ. We consider the zero-temperature regime T = 0.
We solve the model (1) using the dynamical mean-field theory (DMFT) [25,33]. We limit ourselves to paramagnetic solutions in which magnetic ordering is neglected, in order to reveal the pure Mott physics. The lattice problem is mapped onto a quantum impurity problem describing a single d-orbital coupled to an effective electronic bath1. The auxiliary impurity problem is described in terms of the local Weiss field (WF) 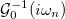 . A self-consistency condition relates the WF to the local properties of the lattice problem:
. A self-consistency condition relates the WF to the local properties of the lattice problem: 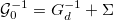 , where Σ is the self-energy function and Gd is the d-component of the local interacting Green's functions, i.e.,
, where Σ is the self-energy function and Gd is the d-component of the local interacting Green's functions, i.e.,

with 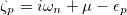 and
and  .
.
The DMFT equations are closed by computing the impurity self-energy 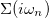 from the numerical solution of the auxiliary impurity problem [25]. In this work we use the exact diagonalization method, in which the effective bath is discretized into a number Nb of levels [34]. The resulting Hamiltonian problem is solved using the Lanczos algorithm to obtain both the lower part of the spectrum and the Green's function [35,36]. The results of this work have been obtained with
from the numerical solution of the auxiliary impurity problem [25]. In this work we use the exact diagonalization method, in which the effective bath is discretized into a number Nb of levels [34]. The resulting Hamiltonian problem is solved using the Lanczos algorithm to obtain both the lower part of the spectrum and the Green's function [35,36]. The results of this work have been obtained with 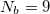 and their robustness with respect to Nb has been tested in selected cases.
and their robustness with respect to Nb has been tested in selected cases.
Mott transition
In the symmetric case (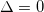 ,
, 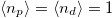 ) the model describes a Kondo insulator for a large enough value of the local hybridization:
) the model describes a Kondo insulator for a large enough value of the local hybridization: 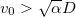 [20] for any interaction strength U. At smaller
[20] for any interaction strength U. At smaller 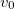 a metal is obtained instead with two bands of mixed
a metal is obtained instead with two bands of mixed  character due to hybridization. In the absence of hybridization the two bands with different orbital character decouple and the d-band describes a half-filled Hubbard system. The latter is known to undergo a zero-temperature Mott transition at a critical interaction strength
character due to hybridization. In the absence of hybridization the two bands with different orbital character decouple and the d-band describes a half-filled Hubbard system. The latter is known to undergo a zero-temperature Mott transition at a critical interaction strength  of the order of the three times the d-band half-bandwidth
of the order of the three times the d-band half-bandwidth 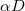 . However, such Mott transition does not survive the presence of any small hybridization [20].
. However, such Mott transition does not survive the presence of any small hybridization [20].
Since no Mott transition can occur in the presence of hybridization in the symmetric model, we move to the mixed-valence regime (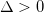 ,
,  ), where the orbital occupations of the two orbitals are different.
), where the orbital occupations of the two orbitals are different.
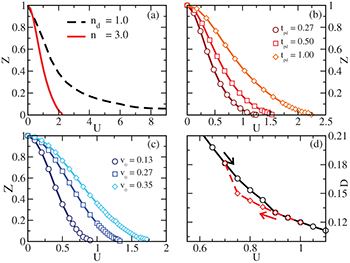
To pinpoint a Mott transition, we compute the quasi-particle residue ![$Z=[1-\partial\Sigma/\partial\omega]^{-1}$](https://content.cld.iop.org/journals/0295-5075/118/1/17004/revision1/epl18531ieqn50.gif) as a function of the interaction strength U (black dashed line). The reduction to zero of this quantity would signal a MIT. We first consider the case of integer filling for the correlated orbitals only. In fig. 1(a) we present results where we actually fix
as a function of the interaction strength U (black dashed line). The reduction to zero of this quantity would signal a MIT. We first consider the case of integer filling for the correlated orbitals only. In fig. 1(a) we present results where we actually fix 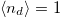 , which implies that the total density is different from an integer number and the p-bands are partially filled. However, as our calculations show, Z remains finite up to huge values of the interaction,
, which implies that the total density is different from an integer number and the p-bands are partially filled. However, as our calculations show, Z remains finite up to huge values of the interaction, 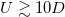 . In this regime the partially filled p-bands provide a delocalization channel for the correlated electrons, ultimately preventing charge localization.
. In this regime the partially filled p-bands provide a delocalization channel for the correlated electrons, ultimately preventing charge localization.
Fig. 1: (Color online) Renormalization constant Z and double occupancy 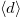 of the correlated band for
of the correlated band for 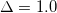 and
and 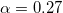 . (a) Z as a function of the interaction U, for either
. (a) Z as a function of the interaction U, for either 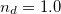 (dashed line) or
(dashed line) or 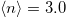 (solid line). The other model parameter are
(solid line). The other model parameter are 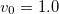 and
and 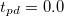 . (b), (c): Z as a function of U for
. (b), (c): Z as a function of U for 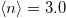 and
and 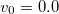 with increasing tpd (b) or
with increasing tpd (b) or 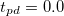 and increasing
and increasing 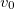 (c). (d) Hysteresis cycle of the double occupancy
(c). (d) Hysteresis cycle of the double occupancy 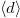 near the Mott transition for
near the Mott transition for 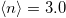 ,
, 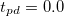 and
and 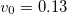 .
.
Download figure:
Standard imageA Mott transition can however be realized in a different regime for any value of the hybridization, as we shall show in the following. On rather general grounds, a sufficiently large hybridization drives the formation of local singlets via the dynamical binding of two electrons on different orbitals [32,37] (see also fig. 2). Thus, a MIT can be realized upon localization of such composite fermionic states for large enough interaction, provided their occupation is one per lattice site. We now show that this is realized for a total density 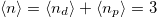 . In fig. 1(a) we report the behavior of Z for this occupation. Our results show that Z approaches zero at a critical value of the correlation
. In fig. 1(a) we report the behavior of Z for this occupation. Our results show that Z approaches zero at a critical value of the correlation 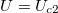 . The existence of a Mott transition in this regime turns out to be generic with respect to the amplitude and the character of the hybridization, as shown in fig. 1(b), (c), where we compare results for local and non-local hybridizations. In both cases we observe the existence of a metal to Mott insulator transition at a critical interaction increasing with the hybridization amplitude. Similarly to the single-band Hubbard model, we find a coexistence of metallic and insulating solutions. This is demonstrated by our results in fig. 1(d), reporting a small hysteresis cycle of the double occupation
. The existence of a Mott transition in this regime turns out to be generic with respect to the amplitude and the character of the hybridization, as shown in fig. 1(b), (c), where we compare results for local and non-local hybridizations. In both cases we observe the existence of a metal to Mott insulator transition at a critical interaction increasing with the hybridization amplitude. Similarly to the single-band Hubbard model, we find a coexistence of metallic and insulating solutions. This is demonstrated by our results in fig. 1(d), reporting a small hysteresis cycle of the double occupation 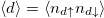 at the d-orbital.
at the d-orbital.
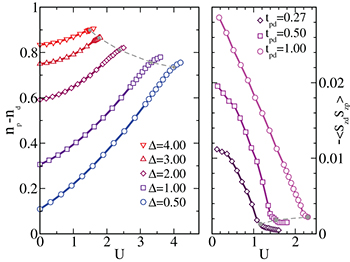
Fig. 2: (Color online) Left panel: orbital polarization  as a function of U for
as a function of U for 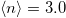 . Data are for increasing Δ and
. Data are for increasing Δ and 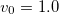 ,
, 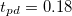 ,
, 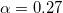 . Right panel: inter-orbital spin-spin correlation
. Right panel: inter-orbital spin-spin correlation 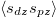 as a function of U. Model parameters are as in fig. 1(b). Grey dotted lines mark the Mott transition points.
as a function of U. Model parameters are as in fig. 1(b). Grey dotted lines mark the Mott transition points.
Download figure:
Standard imageTo better understand the mechanism behind the MIT at 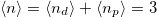 and the absence of a transition for
and the absence of a transition for 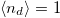 , we follow the evolution of the orbital occupations
, we follow the evolution of the orbital occupations  and
and 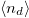 . Our results are summarized in the left panel of fig. 2, which reports the orbital polarization
. Our results are summarized in the left panel of fig. 2, which reports the orbital polarization  as a function of the correlation U. In the integer-valence regime, where a pure-d picture would apply,
as a function of the correlation U. In the integer-valence regime, where a pure-d picture would apply, 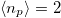 and
and 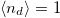 . As shown by our calculations, the system remains in its intermediate-valence regime up and throughout the transition, i.e., the Mott transition occurs with a non-integer value of the individual occupations of the orbitals. Increasing the interaction strength U enhances the orbital polarization, by transferring charge from the correlated orbitals to the uncorrelated orbitals. For a fixed value of U, the orbital polarization naturally increases as a function of the charge-transfer energy Δ. This effect translates the fact that orbital mixing is larger when the two orbitals are brought near one another in energy, and decreases rapidly with increasing energy separation. Indeed, the integer-valence regime can only be reached asymptotically in the Δ → ∞ limit [32].
. As shown by our calculations, the system remains in its intermediate-valence regime up and throughout the transition, i.e., the Mott transition occurs with a non-integer value of the individual occupations of the orbitals. Increasing the interaction strength U enhances the orbital polarization, by transferring charge from the correlated orbitals to the uncorrelated orbitals. For a fixed value of U, the orbital polarization naturally increases as a function of the charge-transfer energy Δ. This effect translates the fact that orbital mixing is larger when the two orbitals are brought near one another in energy, and decreases rapidly with increasing energy separation. Indeed, the integer-valence regime can only be reached asymptotically in the Δ → ∞ limit [32].
In the right panel of fig. 2, we report the evolution of inter-orbital spin-spin correlation 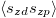 . This quantity describes the binding of the magnetic moments between the d- and p-electrons, which defines the formation of the local singlets. Our results show that the inter-orbital spin-spin correlation remains finite across the MIT, exhibiting the persistence of the local singlets in the Mott state. The decreasing behavior of
. This quantity describes the binding of the magnetic moments between the d- and p-electrons, which defines the formation of the local singlets. Our results show that the inter-orbital spin-spin correlation remains finite across the MIT, exhibiting the persistence of the local singlets in the Mott state. The decreasing behavior of 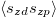 as a function of U results from the renormalization of the hybridization amplitude, which ultimately leads to a loosening of the magnetic binding.
as a function of U results from the renormalization of the hybridization amplitude, which ultimately leads to a loosening of the magnetic binding.
Mott gap opening
In order to investigate the opening of the Mott gap in the intermediate-valence regime, we mapped out the 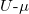 phase diagram, reported in fig. 3. The condition
phase diagram, reported in fig. 3. The condition  determines a line in the metallic part of the diagram intercepting the "V"-shaped Mott insulating region at
determines a line in the metallic part of the diagram intercepting the "V"-shaped Mott insulating region at 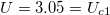 . The metallic solution however disappears inside the insulating region at the critical
. The metallic solution however disappears inside the insulating region at the critical 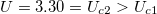 point.
point.
Fig. 3: (Color online) Phase diagram in the 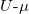 plane. Data are for
plane. Data are for 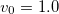 ,
, 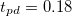 ,
, 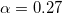 and
and 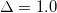 . The (red) solid line is the boundary of the Mott region. The shaded (gray) area indicates the coexistence regions of metallic and insulting solution. The (black) dotted line indicates the
. The (red) solid line is the boundary of the Mott region. The shaded (gray) area indicates the coexistence regions of metallic and insulting solution. The (black) dotted line indicates the 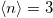 path, ending at
path, ending at 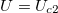 . The symbols mark the points corresponding to
. The symbols mark the points corresponding to 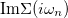 curves in the inset. The (blue) dashed line and points indicate the center of symmetry for the Mott gap (see main text).
curves in the inset. The (blue) dashed line and points indicate the center of symmetry for the Mott gap (see main text).
Download figure:
Standard imageThe opening of the Mott gap is associated to the presence of a pole in the self-energy on the real-axis 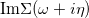 close to
close to 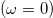 . When the pole is not exactly at zero frequency, the large value of the real part of the self-energy prevents quasiparticle excitations inside the gap. Correspondingly (due to the Kramers-Krönig relations) the imaginary part is found to go to zero at
. When the pole is not exactly at zero frequency, the large value of the real part of the self-energy prevents quasiparticle excitations inside the gap. Correspondingly (due to the Kramers-Krönig relations) the imaginary part is found to go to zero at 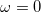 , i.e.,
, i.e., 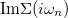 vanishes on the Matsubara axis with a very large linear slope. This is the case for the Mott gap opening along the
vanishes on the Matsubara axis with a very large linear slope. This is the case for the Mott gap opening along the 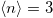 line at
line at 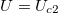 (see fig. 3).
(see fig. 3).
The set of points in the diagram where 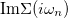 instead diverges, i.e., when the pole of the self-energy is at
instead diverges, i.e., when the pole of the self-energy is at  , it determines the center of symmetry of the Mott gap (see dotted line in fig. 3). In the inset of fig. 3 we detail this condition for the case
, it determines the center of symmetry of the Mott gap (see dotted line in fig. 3). In the inset of fig. 3 we detail this condition for the case  , showing a solution equivalent to the previous one lying at the Mott gap center of symmetry and characterized by a divergent
, showing a solution equivalent to the previous one lying at the Mott gap center of symmetry and characterized by a divergent 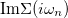 .
.
Phase diagram
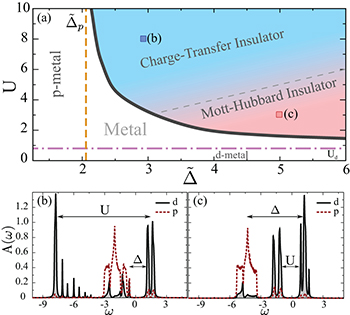
Finally, we studied the dependence of the Mott transition with respect to the charge-transfer energy Δ. Our findings are reported in fig. 4(a), showing the phase diagram in the 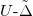 plane, where
plane, where 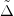 includes the Hartree shift
includes the Hartree shift 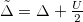 . The diagram closely follows the ZSA diagram [27]. We identify two distinct regimes: A charge-transfer insulator (CTI) for
. The diagram closely follows the ZSA diagram [27]. We identify two distinct regimes: A charge-transfer insulator (CTI) for 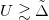 and a Mott-Hubbard insulator (MHI) for
and a Mott-Hubbard insulator (MHI) for 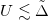 . The different nature of these two insulating solutions is underlined by the spectral functions
. The different nature of these two insulating solutions is underlined by the spectral functions 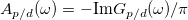 , presented in the bottom panels of the figure. For the CTI (see fig. 4(b)) the smallest gap is of order Δ and corresponds to the excitations from the wide central band, with prevalently p-character, to the upper Hubbard band. Conversely, in the MHI (see fig. 4(c)) the smallest gap is set by the energy separation of the two Hubbard bands of order U. A small coexistence region of metallic and insulating solutions is found. The boundary line for the Mott transition is proportional to
, presented in the bottom panels of the figure. For the CTI (see fig. 4(b)) the smallest gap is of order Δ and corresponds to the excitations from the wide central band, with prevalently p-character, to the upper Hubbard band. Conversely, in the MHI (see fig. 4(c)) the smallest gap is set by the energy separation of the two Hubbard bands of order U. A small coexistence region of metallic and insulating solutions is found. The boundary line for the Mott transition is proportional to 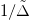 . For large
. For large 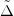 the boundary line approaches the critical value of a Hubbard system for the correlated band only, i.e.,
the boundary line approaches the critical value of a Hubbard system for the correlated band only, i.e.,  (d-metal). This corresponds to the suppression of the indirect delocalization of the correlated electrons of the order of
(d-metal). This corresponds to the suppression of the indirect delocalization of the correlated electrons of the order of 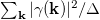 . In the limit of large interaction U a MIT is obtained by closing the charge-transfer gap. For any finite hybridization, there exists a critical charge-transfer energy
. In the limit of large interaction U a MIT is obtained by closing the charge-transfer gap. For any finite hybridization, there exists a critical charge-transfer energy  below which the conduction band crosses the Fermi level. As follows from the structure of eqs. (2), the critical value
below which the conduction band crosses the Fermi level. As follows from the structure of eqs. (2), the critical value 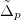 is ultimately determined by the equation
is ultimately determined by the equation  , i.e.,
, i.e., 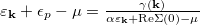 , which corresponds to having a Green's functions pole at the Fermi level, for any value of the interaction (p-metal). The solution of this equation is possible for any
, which corresponds to having a Green's functions pole at the Fermi level, for any value of the interaction (p-metal). The solution of this equation is possible for any 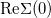 as long as the bare p-band crosses the Fermi level. The absence of this band at the Fermi level is thus a necessary condition for the Mott transition. Since for any fixed hybridization the charge-transfer energy tunes monotonically the density of correlated electrons
as long as the bare p-band crosses the Fermi level. The absence of this band at the Fermi level is thus a necessary condition for the Mott transition. Since for any fixed hybridization the charge-transfer energy tunes monotonically the density of correlated electrons  , this motivates the arising of a non-integer threshold level of
, this motivates the arising of a non-integer threshold level of 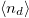 for the Mott transition at large U, as reported in [16] and illustrated by the dashed line in fig. 2(a). This value depends on the other parameters (most notably the hybridization) and is non-universal.
for the Mott transition at large U, as reported in [16] and illustrated by the dashed line in fig. 2(a). This value depends on the other parameters (most notably the hybridization) and is non-universal.
Fig. 4: (Color online) (a) Phase diagram in the 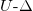 plane, for
plane, for 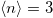 ,
, 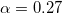 ,
, 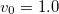 and
and 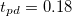 . The (black) solid line delimitates the insulating region, separated from the metallic solution by a first-order transition. The insulating region is divided into two parts: the charge-transfer part (b) and the Mott-Hubbard one (c) (see main text). The lower panels show the spectral densities
. The (black) solid line delimitates the insulating region, separated from the metallic solution by a first-order transition. The insulating region is divided into two parts: the charge-transfer part (b) and the Mott-Hubbard one (c) (see main text). The lower panels show the spectral densities 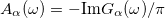 ,
, 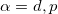 , for the two points (b), (c) in the diagram. The vertical line at
, for the two points (b), (c) in the diagram. The vertical line at 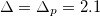 is the boundary of the p-metal regime, while the horizontal line at
is the boundary of the p-metal regime, while the horizontal line at 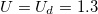 delimitates the d-metal (see main text).
delimitates the d-metal (see main text).
Download figure:
Standard imageThus, the criterion of odd integer total density, including correlated and non-correlated bands, plus the requirement that the bare p-band does not cross the Fermi level, rationalizes the seemingly diverging results of the literature cited in the introduction, under the general perspective of the ZSA diagram [27].
Conclusions
We investigated a paradigmatic model of strongly correlated electrons hybridized with a non-interacting ligand band. We demonstrated that a T = 0 Mott transition occurs for any non-vanishing hybridization amplitude in the mixed-valence regime. This transition corresponds to the Mott localization of singlet states formed by the binding between correlated and conduction band electrons. We point out that a necessary condition for the Mott transition is to have an odd total integer filling 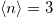 , corresponding to a singlet density of one per site but to a non-integer filling of the correlated orbitals. Thus, we show that the commensuration criteria, a prerequisite for the Mott localization, can be reconciled with the existence of a MIT in a mixed-valence regime, solving the apparent contradiction outlined in the introduction. In a general framework the key control parameter of the Mott insulating state is not the occupation of the correlated orbitals but the density of the local singlets states. Finally, we identify the first-order nature of the transition and discuss the mechanism for the gap opening as well as its dependence on the charge-transfer energy, pointing out that MIT only occurs if the bare p-band does not cross the Fermi level. These results are relevant to understand the physics of d-orbital materials, such as TMO. The extension of this study to the more realistic case of multi-orbital systems, which better capture the physics of t2g and eg orbitals and their different hybridization with ligand atoms in TMO, is an interesting future direction of research. Similarly, understanding the role of a more realistic form of the interaction, including other inter- and intra-orbital terms [18] as well as the impact of Hund's exchange on the orbital fluctuations in these systems, is a challenging future development of this research.
, corresponding to a singlet density of one per site but to a non-integer filling of the correlated orbitals. Thus, we show that the commensuration criteria, a prerequisite for the Mott localization, can be reconciled with the existence of a MIT in a mixed-valence regime, solving the apparent contradiction outlined in the introduction. In a general framework the key control parameter of the Mott insulating state is not the occupation of the correlated orbitals but the density of the local singlets states. Finally, we identify the first-order nature of the transition and discuss the mechanism for the gap opening as well as its dependence on the charge-transfer energy, pointing out that MIT only occurs if the bare p-band does not cross the Fermi level. These results are relevant to understand the physics of d-orbital materials, such as TMO. The extension of this study to the more realistic case of multi-orbital systems, which better capture the physics of t2g and eg orbitals and their different hybridization with ligand atoms in TMO, is an interesting future direction of research. Similarly, understanding the role of a more realistic form of the interaction, including other inter- and intra-orbital terms [18] as well as the impact of Hund's exchange on the orbital fluctuations in these systems, is a challenging future development of this research.
Acknowledgments
The authors are indebted with M. J. Rozenberg, G. Sangiovanni and A. Valli for useful discussions. Financial support from the European Research Council under FP7 Starting Independent Research Grant No. 240524 "SUPERBAD" and the Seventh Framework Programme FP7, under Grant No. 280555 "GO FAST" and under H2020 Framework Programme, ERC Advanced Grant No. 692670 "FIRSTORM" are acknowledged.
Footnotes
- 1
An equivalent representation can be obtained considering a
 dimer embedded in a self-consistent bath, see [33].
dimer embedded in a self-consistent bath, see [33].