Abstract
We report a joint experimental and theoretical investigation of cyclic training of amorphous frictional granular assemblies, with special attention to memory formation and retention. Measures of dissipation and compactification are introduced, culminating with a proposed scaling law for the reducing dissipation and increasing memory. This scaling law is expected to be universal, and insensitive to the details of the elastic and frictional interactions between the granules.
Export citation and abstract BibTeX RIS
"Memory" in materials physics is usually associated with the existence of macroscopic hysteretic responses [1]. Two distinct states, separated by a potential barrier larger than the thermal energy scale, can be used as a memory-encoding mechanism; magnetic hysteresis being the most famous example from physics and the basis for all magnetic information storage media [2]. Memory formation and retention via hysteresis is a non-equilibrium process because the system requires external forcing to get across the energy barrier from one state to the other. Consequently, universal laws and universal exponents which provide adequate theoretical characterization of equilibrium transitions are very difficult to find in non-equilibrium hysteretic processes.
Friction-induced hysteresis as well as memory in amorphous granular media is well known in the context of rock geophysics [3] and engineering [4,5], but the mechanism of memory formation, its training, and eventual retention are not yet well understood [6]. Furthermore, the strong protocol dependence and the granular pack's preparation history immediately dash any hope of observing universal behavior in these systems. Here we focus on memory that is induced by training a frictional granular matter by cyclic loading and unloading [7–13]. In each such cycle dissipation leads to hysteresis, but with repeated cycles the dissipation diminishes until the system retains memory of an asymptotic loaded state that is not forgotten even under complete unloading. We report and explain a universal power law associated with the reduced dissipation and increase in memory which is expected to hold irrespectively of the details of the microscopic interactions.
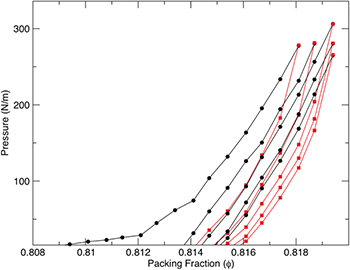
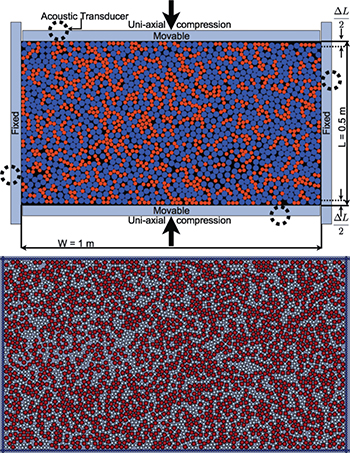
The phenomenon under study is best introduced by the experimental plots of pressure vs. packing fraction obtained by compressing and decompressing uniaxially an array of frictional disks [11], cf. fig. 1. The experimental setup is detailed in the Supplementary Material Supplementarymaterial.pdf (SM). A typical example of the experimental cell is shown in the upper panel of fig. 2. Two opposing boundaries separated by the chamber length L were movable while the other two (transverse) boundaries were held fixed. The two opposing movable boundaries provided uni-axial pack compression, through which the packing fraction Φ was controlled. Accordingly, we define the packing fraction Φ as the ratio of the total area occupied by the disks to the chamber area bounded within the four boundaries, two of which are movable. Figure 1 displays a typical series of consecutive loops of compression-decompression loops; the coarse-grained data was collected in quasi-static steps 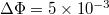 for representational purposes. The qualitative experimental observation is that the area in consecutive hysteresis loops diminishes monotonically while the packing fraction is increasing with every loop. This indicates that the system is compacted further with every loop and this process is accompanied by a reduction in the dissipation. The experimental results left however two open questions: i) whether asymptotically the dissipation vanished, such that every compression became purely elastic and the decompression to zero pressure left the system with perfect memory of the stressed configuration; and ii) whether there is anything universal in the way that the areas of the loops approach their asymptote, be them finite or zero. To answer these question we performed numerical simulations that lead to the conclusion that i) asymptotically the hysteresis loops are still dissipative due to frictional losses, but the structural rearrangements disappear and the neighbor list becomes invariant; and ii) that the area An under the n-th hysteresis loop (which is a direct measure of the dissipation) decays as a power law to an asymptotic value according to
for representational purposes. The qualitative experimental observation is that the area in consecutive hysteresis loops diminishes monotonically while the packing fraction is increasing with every loop. This indicates that the system is compacted further with every loop and this process is accompanied by a reduction in the dissipation. The experimental results left however two open questions: i) whether asymptotically the dissipation vanished, such that every compression became purely elastic and the decompression to zero pressure left the system with perfect memory of the stressed configuration; and ii) whether there is anything universal in the way that the areas of the loops approach their asymptote, be them finite or zero. To answer these question we performed numerical simulations that lead to the conclusion that i) asymptotically the hysteresis loops are still dissipative due to frictional losses, but the structural rearrangements disappear and the neighbor list becomes invariant; and ii) that the area An under the n-th hysteresis loop (which is a direct measure of the dissipation) decays as a power law to an asymptotic value according to

Here  represents the dissipation due to frictional slips that exist even in the asymptotic loop, and it depends on the material properties. The second term in eq. (1) is due to the successive compactification of the sample, and the constant B is also expected to depend on material properties. The form of this law, however, is universal, expected to hold independently of the details of the microscopic interaction between the granules.
represents the dissipation due to frictional slips that exist even in the asymptotic loop, and it depends on the material properties. The second term in eq. (1) is due to the successive compactification of the sample, and the constant B is also expected to depend on material properties. The form of this law, however, is universal, expected to hold independently of the details of the microscopic interaction between the granules.
Fig. 1: (Color online) Representative coarse-grained  hysteresis loops obtained experimentally upon uniaxial compression and decompression of an amorphous configuration of frictional disks as will be seen in fig. 2. The pressure P is measured in N/m, and Φ is dimensionless. Compression legs are in black and decompression in red.
hysteresis loops obtained experimentally upon uniaxial compression and decompression of an amorphous configuration of frictional disks as will be seen in fig. 2. The pressure P is measured in N/m, and Φ is dimensionless. Compression legs are in black and decompression in red.
Download figure:
Standard imageFig. 2: (Color online) Upper panel: an example of a typical initial configuration in the experiment. Lower panel: an example of a typical initial configuration in the numerical simulation.
Download figure:
Standard imageThe details of the numerical set up are provided in the SM. An example of an initial configuration is shown in the lower panel of fig. 2. We assign a Hertzian normal force 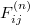 and a Mindlin tangential force
and a Mindlin tangential force 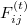 [14–18] to each binary contact ij. The tangential force is always limited by the Coulomb law
[14–18] to each binary contact ij. The tangential force is always limited by the Coulomb law

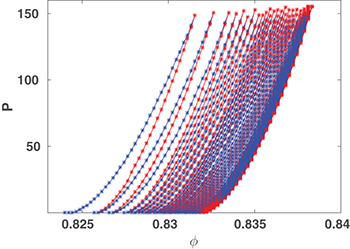
In uniaxial straining the pressure is increased by pushing two opposite walls of the system towards each other. In each cycle we first reach a chosen maximal pressure by quasi-static steps. After each compression step, the system is allowed to relax to reach a new mechanical equilibrium in which the global stress tensor is measured by averaging the dyadic products between all the binary contact forces and the vectors connecting the centers of mass in a given volume. The trace of this stress tensor is the new pressure P. After a full compression leg, a cycle is completed by decompressing back to zero pressure, where the next compression cycle begins. The packing fraction Φ is monitored throughout this process. Each such cycle traces a hysteresis loop in the P-Φ plane, see fig. 3 as an example. The area within each hysteresis loop is a measure of the dissipation, which in general stems from two sources. One are plastic events in which the neighbor lists change in an irreversible fashion, and the other is due to frictional losses when the frictional tangential force exceeds the allowed Coulomb limit. The training of the system is exemplified by the fact that the dissipation as measured by the area An of the n-th cycle reduces with n and reaches an asymptotic value when  . Measuring the area in the n-th loop we find that it follows a power law decay in the form of eq. (1) The data supporting this power law are exhibited in fig. 4. From this data we can conclude that
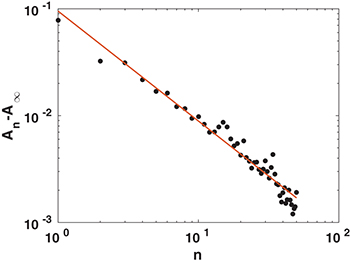
. Measuring the area in the n-th loop we find that it follows a power law decay in the form of eq. (1) The data supporting this power law are exhibited in fig. 4. From this data we can conclude that  and that the scaling law appears universal with respect to changes in the value of μ. A further evidence of universality is obtained by changing the size distribution of disks, choosing a multi-dispersed system with radii ratios 1, 1.1, 1.2 and 1.4. Identical power laws were found. To understand the scaling law we need to identify the two important processes that take place during the cyclic training. One is compactification. In every compression leg of the cycle the system compactifies, until a limiting Φ value is reached for the chosen maximal pressure. To quantify this process we can measure the volume fraction
and that the scaling law appears universal with respect to changes in the value of μ. A further evidence of universality is obtained by changing the size distribution of disks, choosing a multi-dispersed system with radii ratios 1, 1.1, 1.2 and 1.4. Identical power laws were found. To understand the scaling law we need to identify the two important processes that take place during the cyclic training. One is compactification. In every compression leg of the cycle the system compactifies, until a limiting Φ value is reached for the chosen maximal pressure. To quantify this process we can measure the volume fraction  at the highest value of the pressure in the n-th cycle. Define then a new variable
at the highest value of the pressure in the n-th cycle. Define then a new variable

This new variable is history dependent in the sense that 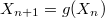 , where the function g(x) is unknown at this point. This function must have a fixed point
, where the function g(x) is unknown at this point. This function must have a fixed point  since the series
since the series  must converge; for any given chosen maximal pressure there is a limiting volume fraction that cannot be exceeded. Near the fixed point, assuming analyticity, we must have the form
must converge; for any given chosen maximal pressure there is a limiting volume fraction that cannot be exceeded. Near the fixed point, assuming analyticity, we must have the form

Of course, special circumstances may result in C = 0 and a starting nonlinear term being proportional to  . Also, if there is a reason for non-analyticity, the exponent may be non-integer. But these circumstance are expected to be non-generic for the problem at hand and eq. (4) is expected to be the generic "normal form" near the fixed point
. Also, if there is a reason for non-analyticity, the exponent may be non-integer. But these circumstance are expected to be non-generic for the problem at hand and eq. (4) is expected to be the generic "normal form" near the fixed point  . The solution of this equation for large n is
. The solution of this equation for large n is

The area under the n-th loop is directly related to Xn since 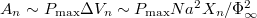 , where
, where  is the change in volume and
is the change in volume and 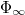 is the asymptotic packing fraction. Thus, eq. (5) is the source of the second term in eq. (1), which stems from the compactification that reduces the amount of dissipation due to irreversible plastic rearrangements. A direct measurement of Xn as a function of n is shown in the log-log plot presented in fig. 5, supporting the generality of this power law. Without any reason for non-analyticity in the function g(Xn) this conclusion is firm. It should be noted at this point that the scaling laws eqs. (1) and (5) must contain some logarithmic corrections, since the harmonic series does not converge, but the series
is the asymptotic packing fraction. Thus, eq. (5) is the source of the second term in eq. (1), which stems from the compactification that reduces the amount of dissipation due to irreversible plastic rearrangements. A direct measurement of Xn as a function of n is shown in the log-log plot presented in fig. 5, supporting the generality of this power law. Without any reason for non-analyticity in the function g(Xn) this conclusion is firm. It should be noted at this point that the scaling laws eqs. (1) and (5) must contain some logarithmic corrections, since the harmonic series does not converge, but the series 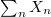 must converge to get an asymptotic value of
must converge to get an asymptotic value of 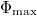 . Indeed, the scaling laws measured above consistently show exponents slightly smaller than −1, and, therefore, the series of
. Indeed, the scaling laws measured above consistently show exponents slightly smaller than −1, and, therefore, the series of 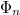 converges. It is very likely that this small difference is due to logarithmic corrections to the scaling law which cannot be computed from the simple theory presented here.
converges. It is very likely that this small difference is due to logarithmic corrections to the scaling law which cannot be computed from the simple theory presented here.
Fig. 3: (Color online) A succession of hysteresis loops as measured in the numerical simulation. Blue symbols are compression legs and red symbols decompression legs. Here 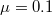 .
.
Download figure:
Standard imageFig. 4: (Color online) The power law for the decaying areas under the hysteresis loops as measured in the numerical simulation. Here 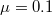 , Black dots are data and the red line is the best-fitting power law
, Black dots are data and the red line is the best-fitting power law 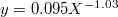 . The observed lot is independent of μ, cf. the SM.
. The observed lot is independent of μ, cf. the SM.
Download figure:
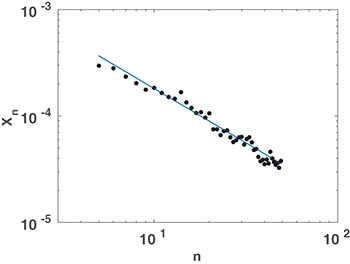
Standard imageFig. 5: (Color online) Log-log plot of Xn vs. n. The black dots are the data, the blue line is the best-fitting scaling law 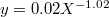 . The data corroborates eq. (5).
. The data corroborates eq. (5).
Download figure:
Standard imageThe first term in eq. (1), on the other hand, is due to the frictional dissipation. In uniaxial compression there is a shear component, and the shear stress loads the tangential contacts. Whenever the tangential force exceeds the Coulomb limit, eq. (2), the system dissipates some energy to a frictional slip. Even if the neighbor list becomes invariant at large values of n, the loading of the system is always accompanied by frictional slips. In our simulations we can measure the energy dissipated by friction slips, denoted as 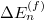 in the n-th hysteresis loop. To have a non-dimensional measure we normalized this quantity by
in the n-th hysteresis loop. To have a non-dimensional measure we normalized this quantity by 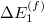 , denoting the result as Sn. The dependence of this normalized dissipated energy on n is presented in fig. 6. It is clear that the normalized dissipated energy due to frictional slips reduces rapidly to a stable value; this is the first term in eq. (1).
, denoting the result as Sn. The dependence of this normalized dissipated energy on n is presented in fig. 6. It is clear that the normalized dissipated energy due to frictional slips reduces rapidly to a stable value; this is the first term in eq. (1).
Fig. 6: The normalized frictional energy loss in each hysteresis loop. This energy loss drops to a stable value that is responsible for the asymptotic dissipation that is encoded by the area 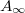 in eq. (1).
in eq. (1).
Download figure:
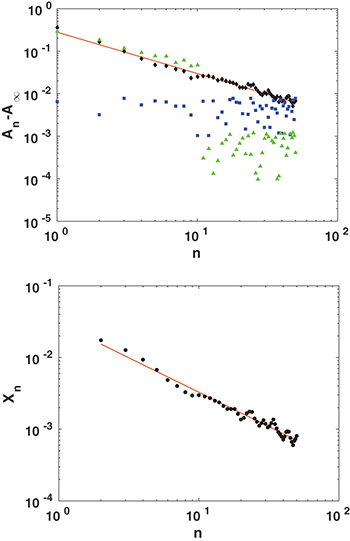
Standard imageEncouraged by this theory we returned to the experimental data to measure both Xn and An. To obtain the logarithmic n dependence of the area we needed to know the value of 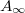 . A direct measurement of this area is unfeasible. But one recognizes that the total dissipation under the asymptotic loop should be the same with or without memory. Accordingly, we applied an acoustic perturbation to the configuration after each quasi-static step to destroy memory and training, and force the system to go to asymptotic state. The result is shown in the upper panel of fig. 7, showing
. A direct measurement of this area is unfeasible. But one recognizes that the total dissipation under the asymptotic loop should be the same with or without memory. Accordingly, we applied an acoustic perturbation to the configuration after each quasi-static step to destroy memory and training, and force the system to go to asymptotic state. The result is shown in the upper panel of fig. 7, showing 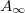 alone in blue squares. Indeed
alone in blue squares. Indeed 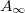 is finite and flat as a function of n. Using the measured value of
is finite and flat as a function of n. Using the measured value of 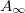 we get the power law scaling for
we get the power law scaling for 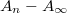 as expected and as shown by the data with black rhombi. To underline the fact that this scaling law is governed by the memory during the training protocol we demonstrate the change that is caused by destroying the memory midway through the cycles; this is a further validation that the power law is indeed coming from training and memory formation. For the data shown in green triangles, there are no acoustic perturbations for n = 1−10; there we see the power law behavior. From n = 11−50, we apply acoustic perturbations after each quasi-static step. The loop areas now fall drastically and become flat. Note that the magnitude is below
as expected and as shown by the data with black rhombi. To underline the fact that this scaling law is governed by the memory during the training protocol we demonstrate the change that is caused by destroying the memory midway through the cycles; this is a further validation that the power law is indeed coming from training and memory formation. For the data shown in green triangles, there are no acoustic perturbations for n = 1−10; there we see the power law behavior. From n = 11−50, we apply acoustic perturbations after each quasi-static step. The loop areas now fall drastically and become flat. Note that the magnitude is below 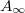 since we are plotting the difference
since we are plotting the difference 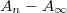 .
.
Fig. 7: (Color online) Upper panel: the areas 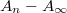 measured experimentally as a function of n, agreeing to eq. (1) with
measured experimentally as a function of n, agreeing to eq. (1) with 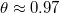 ; black rhombi. Blue squares: the estimate of
; black rhombi. Blue squares: the estimate of 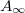 obtained by forcing the system to the asymptote by acoustic perturbations. Green triangles: the areas resulting from the destruction of memory after 10 regular loops. Lower panel: experimental results for Xn shown in log-log plot vs. n; the slope is approximately 0.96.
obtained by forcing the system to the asymptote by acoustic perturbations. Green triangles: the areas resulting from the destruction of memory after 10 regular loops. Lower panel: experimental results for Xn shown in log-log plot vs. n; the slope is approximately 0.96.
Download figure:
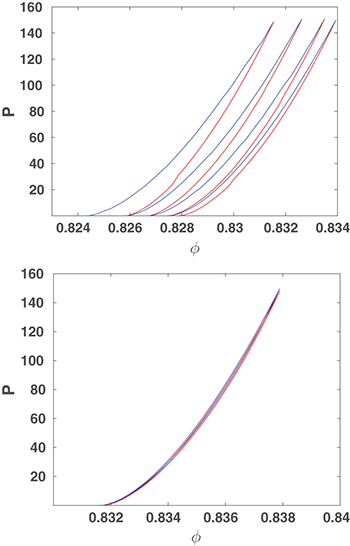
Standard imageIt should be commented that the simple scenario discussed in the letter requires a subtle change in the shape of the hysteresis loops. The low-order loops are increasing the volume fraction, such that the compression leg starts with a lower value of Φ than the end of the decompression loop, see the upper panel in fig. 8. This continues to be the case as long as the systems can be compactified further. The high-order loops must begin and end at the same value of 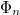 , see the lower panel in fig. 8. Thus, for large value of n the hysteresis loops become repetitive, with an invariant trace in the P-Φ plane, even though they have frictional dissipation in the limit
, see the lower panel in fig. 8. Thus, for large value of n the hysteresis loops become repetitive, with an invariant trace in the P-Φ plane, even though they have frictional dissipation in the limit 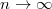 . This subtle change in the shape of the hysteresis loops allows the function g(x) to have the fixed point at x = 0 around which the analytic expansion dictates the universality of the power law.
. This subtle change in the shape of the hysteresis loops allows the function g(x) to have the fixed point at x = 0 around which the analytic expansion dictates the universality of the power law.
Fig. 8: (Color online) Upper panel: examples of low-order hysteresis loops in the P-Φ plane. The compression legs are blue and the decompression legs red. Lower panel: examples of higher-order hysteresis loops in the P-Φ plane with the same color convention. The high-order loops are no longer able to compactify the system further, and the compression leg begins at the same volume fraction where the decompression leg ends.
Download figure:
Standard imageIn conclusion, we presented and explained a universal scaling law in the context of the cyclic training of an amorphous assembly of frictional disks. The protocol exhibits a reduction in the dissipation per loop until the system reaches an asymptotic configuration with maximal volume fraction (for the maximal pressure chosen in the cyclic protocol). Once achieved, the system has a perfect memory of the stressed state even when it is completely decompressed to zero pressure. Interestingly enough, repeated compressions are not without dissipation, since shear always induces frictional slips. But the beginning and final volume fractions become invariant and the system repeats exactly the same hysteresis loop in the P-Φ space. The amount of dissipation in the cyclic loops is governed by the scaling law, eq. (1), which has a universal form with material-dependent coefficients. The two terms in this equation were identified and related to the dissipation due to changes in the neighbor list and the frictional slips, respectively.
Acknowledgments
This work has been supported in part by the US-Israel BSF and the ISF joint grant with Singapore. IP is indebted to the Niels Bohr International Academy for its hospitality under the Simons Fellowship where this paper was written. MMB and the experiments were supported by the Collective Interactions Unit, OIST Graduate University. MMB gratefully acknowledges being graciously hosted by Prof. Surajit Sengupta and TCIS, TIFR while working on this paper.