Abstract
All liquid three-layer batteries are intended as large-scale electrical energy storage. The paper investigates long-wave interfacial instabilities driven by the electromagnetic forces during dynamic phases of the battery charging/discharging. The liquid metal battery of 20 cm size with sodium metal anode, which is a candidate for experimental and commercial implementation, is shown to be unstable at the discharge state when the top metal layer depth is reduced below a critical level. The numerical model includes the effects of viscous friction and the horizontal wave velocities. The instability does not depend on the initial interface perturbation type.
Export citation and abstract BibTeX RIS
Introduction
With the advancement of renewable intermittent energy sources the idea of Liquid Metal Battery (LMB) as a device for stationary energy storage is gaining attention [1]. The development of small-scale (about few cm) prototypes demonstrates technical feasibility of the battery and its advantages to existing solid batteries [1,2]. The liquid state of the main components necessitates consideration of the fluid dynamics in the LMBs. A number of recent publications are devoted to the problem: a possibility of the Tayler instability [3,4], the thermal convection [5], observation of a vortical flow in the LMB model [6], as well as the electromagnetically driven wave instability in the stratified three-liquid-layer system [7–12]. The main motivation of these investigations is to gain understanding of the liquid mixing, the charge and mass tansfer, and a possibility of electro-magnetically driven destabilizing interface motion.
LMBs are thought to be easily scalable due to their simple construction using the natural density stratification of the liquid layers. The magneto-hydrodynamic stability of the liquid filled cells could be problematic with the upscaling. As was shown in [7], large cells of several cubic meters total volume can be designed to operate safely at very high power value ( W). The same high power and storage capacity could be achieved using a large cluster of small LMBs [1,8]. However in both cases high current densities in the cells will be coupled to the total magnetic field (created by the currents in the cell, the supply bars and the neighbour cells) leading to significant electromagnetic forces. Such forces in stratified liquid layers with free surface areas may cause the long-wave interfacial instability as is well known in the case of Hall-Héroult Cells (HHC) [13–15]. The manifestation of this instability in the small-scale LMB at various stages of discharge, when the metal levels change, is the subject of this paper. The previously developed theoretical and numerical models [12] will be applied to analyze the interfacial waves in the small-scale LMB filled with three liquid layers (fig. 1) composed of Na∣ NaF-NaCl-NaI∣ Bi [1,2]. The liquid sodium is considered as one of attractive and relatively safe anodic materials to be used in the upscaling physical experiments.
W). The same high power and storage capacity could be achieved using a large cluster of small LMBs [1,8]. However in both cases high current densities in the cells will be coupled to the total magnetic field (created by the currents in the cell, the supply bars and the neighbour cells) leading to significant electromagnetic forces. Such forces in stratified liquid layers with free surface areas may cause the long-wave interfacial instability as is well known in the case of Hall-Héroult Cells (HHC) [13–15]. The manifestation of this instability in the small-scale LMB at various stages of discharge, when the metal levels change, is the subject of this paper. The previously developed theoretical and numerical models [12] will be applied to analyze the interfacial waves in the small-scale LMB filled with three liquid layers (fig. 1) composed of Na∣ NaF-NaCl-NaI∣ Bi [1,2]. The liquid sodium is considered as one of attractive and relatively safe anodic materials to be used in the upscaling physical experiments.
Fig. 1: Schematic representation of the 3-layer LMB model.
Download figure:
Standard imageThe numerical models will be applied to answer the questions about the two interface coupling, the importance of the initial perturbation conditions and the destabilizing effect of the metal level change during the charging/discharging process.
The governing equations
The model of battery consisting of three density stratified electrically conductive liquid layers contained in a rectangular box is schematically represented in fig. 1. The full mathematical model derivation is presented in [12], therefore we will emphasize here only the main points leading to the coupled wave and electric current equations.
Coupled interfacial dynamics
The incompressible laminar fluid flow in the presence of electro-magnetic fields is described by the equations


where the indices  correspond to the coordinates (x, y, z), the velocity components are given as (u1, u2, u3), the summation over repeated indices is implied, ρ represents the density, ν the kinematic viscosity, g the gravitational acceleration, p the pressure and
correspond to the coordinates (x, y, z), the velocity components are given as (u1, u2, u3), the summation over repeated indices is implied, ρ represents the density, ν the kinematic viscosity, g the gravitational acceleration, p the pressure and  stands for the electromagnetic force vector, whereas j is the electric current density and B the magnetic field. The horizontal dimensions of the cell are assumed to be much larger compared to the vertical depth of layers, so that the description can be based on a systematically derived shallow-water approximation. The velocity components can be represented as an expansion in a small aspect ratio parameter
stands for the electromagnetic force vector, whereas j is the electric current density and B the magnetic field. The horizontal dimensions of the cell are assumed to be much larger compared to the vertical depth of layers, so that the description can be based on a systematically derived shallow-water approximation. The velocity components can be represented as an expansion in a small aspect ratio parameter  , where h is a typical depth (e.g., of the unperturbed layer) and L is the characteristic horizontal dimension (width of the cell):
, where h is a typical depth (e.g., of the unperturbed layer) and L is the characteristic horizontal dimension (width of the cell):

The leading horizontal components of (1) for  are
are

for the depth averaged velocity components when using the shallow-water linear friction law (the value of kf is given below in (26)). The depth averaged horizontal velocity components are defined as

where  is the layer number,
is the layer number,  is the local variable depth, see the fig. 1.
is the local variable depth, see the fig. 1.
The vertical component i = 3 of the eq. 1 gives the hydrostatic pressure distribution in the liquid layers accounting for the variable interface shapes H1(x, y, t) and H2(x, y, t) [12]. The depth averaged continuity eq. (2) is accurate to all orders of approximation:

The equations can be linearized if an additional approximation of a small wave amplitude is introduced:  for the layer thickness, or equivalently
for the layer thickness, or equivalently  for the interface position,
for the interface position,  , where A is a typical wave amplitude and h0k, H0k are the unperturbed values. For typical geometries considered in this paper
, where A is a typical wave amplitude and h0k, H0k are the unperturbed values. For typical geometries considered in this paper  , and
, and  . The small depth approximation
. The small depth approximation  is just marginally satisfied in some cases considered below, however the 3-layer wave frequencies are mostly affected by the presence of the shallow intermediate layer (
is just marginally satisfied in some cases considered below, however the 3-layer wave frequencies are mostly affected by the presence of the shallow intermediate layer ( ), therefore permitting a meaningful approximation in the 3-layer problem.
), therefore permitting a meaningful approximation in the 3-layer problem.
The wave equations for the coupled interfaces H1 and H2 can be derived following the procedure described in [12]:


where the depth averaged force density Fi is defined similarly to (5). The electromagnetic terms are of the same order of magnitude as the leading terms, while the nonlinear wave motion terms are of lower order ( ). The boundary condition for the normal velocity
). The boundary condition for the normal velocity  at the side walls leads to the condition [12]:
at the side walls leads to the condition [12]:

for  . The constants introduced in the above equations are defined as
. The constants introduced in the above equations are defined as

Note that in (7) and (8) the summation over repeated indices is limited to the two horizontal dimensions  . Equations (7), (8) include additional terms to the similar wave equations obtained in [11], particularly the viscous friction, generalised electromagnetic force and the horizontal velocity effects. The MHD wave model for the aluminium electrolysis cell [15] with the single interface H1(x, y, t) can be recovered from (7) if the top interface is constant in time:
. Equations (7), (8) include additional terms to the similar wave equations obtained in [11], particularly the viscous friction, generalised electromagnetic force and the horizontal velocity effects. The MHD wave model for the aluminium electrolysis cell [15] with the single interface H1(x, y, t) can be recovered from (7) if the top interface is constant in time:  .
.
If neglecting the electro-magnetic and the dissipation terms, eqs. (7)–(9) can be solved to obtain the expressions for the 2 coupled interface gravity wave frequencies [9,11,12]:

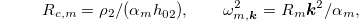
showing the correlation between the uncoupled shallow-layer gravity wave frequencies  and the coupled two interface frequencies
and the coupled two interface frequencies  . The wave vector k is defined as
. The wave vector k is defined as

Equation (11) describes the two sets of self-sustained wave frequencies on both interfaces with the "−" sign corresponding to the so-called "slow" mode and the "+" sign to the "fast" mode [9,12]. This expression will be useful to compare the pure gravity wave frequencies to the electromagnetically modified waves and the frequency at which instability starts
Electric current flow
The LMB operates in a dynamic regime of charging or discharging, resulting in the current flowing upwards or downwards. The current flow at the discharging stage in the layered structure is illustrated in fig. 1. We assume that the characteristic time-scale for the wave motion is much larger than the diffusion time of the magnetic field to satisfy the low magnetic Reynolds number approximation and the flow effect on the instantaneous current distribution can be neglected, so that the electric current can be described by a set of coupled Laplace equations for the electric potential  :
:

where  corresponds to the layer number. The continuity conditions for the electric potential and the normal current component
corresponds to the layer number. The continuity conditions for the electric potential and the normal current component  at the interfaces
at the interfaces  are
are

The normal derivatives at the deformed interfaces are defined as

assuming the summation over the repeated index i only. The side walls of the domain are considered to be electrically insulating. The applied current distributions at the top and the bottom of the cell could be given from the external circuit solution [13], however here for simplicity we assume the supply current to be uniform and equal:

The shallow-layer approximation for the 3d electric current requires the expansion of the electric potential in terms of the parameters δ and ε [12,15]:



where the 2d functions ak, Ak, bk, Bk, ck, Ck(x, y) are determined from the set of interfacial conditions (14). After a lengthy derivation the final equations for the perturbation potentials defined as  and
and  can be obtained [12]:
can be obtained [12]:


According to (20) and (21), the perturbed current flow is determined by the electrolyte thickness variations and the ratio of the electrical conductivities. The dimensional current components in the three layers can be expressed as



To the given perturbation accuracy the horizontal currents in liquid metal layers are depth independent and the vertical current is linearly varying from the imposed supply value to the wave perturbed distribution at the electrolyte. The current distribution in the electrolyte is almost purely vertical due to the relatively low conductivity  . The terms in the left side of (20), (21) are of equal order proportional to
. The terms in the left side of (20), (21) are of equal order proportional to  . Similar equations to (20), (21), however without the terms containing the perturbed potential differences, have been derived in [11].
. Similar equations to (20), (21), however without the terms containing the perturbed potential differences, have been derived in [11].
Numerical solution construction
The solution of the problem can be constructed using the spectral representation in Fourier space [12,15]. The following set of functions is introduced:

 and
and  are the spectral wave amplitudes and the perturbed potentials in Fourier space, k is defined in (12) and
are the spectral wave amplitudes and the perturbed potentials in Fourier space, k is defined in (12) and  is the normalization coefficient. Equations (7), (8), (20), (21) are represented in the spectral space using the expansions (25). The second-order implicit central finite difference scheme is used to approximate the time derivatives when solving the wave evolution problem. The physical variables are reconstructed using (25).
is the normalization coefficient. Equations (7), (8), (20), (21) are represented in the spectral space using the expansions (25). The second-order implicit central finite difference scheme is used to approximate the time derivatives when solving the wave evolution problem. The physical variables are reconstructed using (25).
Results
The following numerical study is intended to study a specific liquid metal battery proposed as a candidate for physical experiments and possible commercial implementation. The battery contains sodium metal as the anodic top layer, bismuth-sodium alloy as the bottom cathode and the liquid salt composed of NaF-NaCl-NaI (the material properties [1] are given in table 1). The cell is square in the horizontal section with the dimensions:  , similar as proposed in [8] for a circular cell of radius 0.2 m. The applied total electric current is fixed at the value I = 130 A (
, similar as proposed in [8] for a circular cell of radius 0.2 m. The applied total electric current is fixed at the value I = 130 A ( ). The magnetic field typical of this cell can be estimated on the dimensional grounds:
). The magnetic field typical of this cell can be estimated on the dimensional grounds:  . In accordance to the previous studies [8–15] the interfacial stability is crucially affected by the vertical component of the magnetic field, therefore we choose the field as
. In accordance to the previous studies [8–15] the interfacial stability is crucially affected by the vertical component of the magnetic field, therefore we choose the field as  , with
, with  . It is assumed that the flow is purely laminar, which permits to use the shallow-layer friction coefficient derived from the gravity wave damping rate for long waves according to [16] including the bottom and the side wall friction:
. It is assumed that the flow is purely laminar, which permits to use the shallow-layer friction coefficient derived from the gravity wave damping rate for long waves according to [16] including the bottom and the side wall friction:

Table 1:. Material properties of a Na∥Bi battery at the operating temperature T = 560 °C [1].
| Liquid |  (kg/m3) (kg/m3) |
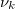 (m2/s) (m2/s) |
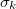 (S/m) (S/m) |
|---|---|---|---|
| Bi | 9720 | 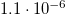 |
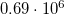 |
| NaF-NaCl-NaI | 2540 | 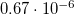 |
200 |
| Na | 831 |  |
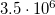 |
During the charge and discharge the liquid metal levels are changing, which can affect the interfacial stability at various stages. The effect was analysed considering three different metal layer thickness combinations: the fully charged case, intermediate situation, and the final discharged case. The total liquid height is assumed to be constant:  , and the electrolyte thickness is constant:
, and the electrolyte thickness is constant:  in all cases. A small initial wave perturbation corresponding to the long gravity wave of the mode (m = 1, n = 0) of amplitude
in all cases. A small initial wave perturbation corresponding to the long gravity wave of the mode (m = 1, n = 0) of amplitude  was applied at the upper interface:
was applied at the upper interface:  , while the lower interface was initially unperturbed, but involved in the dynamic simulation following the top perturbation. The results of the direct wave evolution problem solution are summarized in fig. 2. On the left side figs. 2(a), (c), (e) show interfacial oscillations at a fixed position in the left corner of the cell (x = 0, y = 0 in fig. 1). On the right side figs. 2(b), (d), (f) show the respective computed Fourier power spectra appearing as vertical narrow peaks. The triangles located at the horizontal axis represent the theoretical three-layer gravity frequencies defined by (11) in the absence of the electromagnetic interaction.
, while the lower interface was initially unperturbed, but involved in the dynamic simulation following the top perturbation. The results of the direct wave evolution problem solution are summarized in fig. 2. On the left side figs. 2(a), (c), (e) show interfacial oscillations at a fixed position in the left corner of the cell (x = 0, y = 0 in fig. 1). On the right side figs. 2(b), (d), (f) show the respective computed Fourier power spectra appearing as vertical narrow peaks. The triangles located at the horizontal axis represent the theoretical three-layer gravity frequencies defined by (11) in the absence of the electromagnetic interaction.
Fig. 2: (Colour online) The coupled interface oscillations (left) and the Fourier power spectra (right) for different metal levels during the battery discharge: (a), (b):  ,
,  ; (c), (d):
; (c), (d):  ; (e), (f):
; (e), (f):  ,
,  .
.
Download figure:
Standard imageWhen the cell is at the fully charged state the bottom metal layer is thinner than the top one:  ,
,  . The resulting motion of the waves generated at both interfaces is stable in this case (figs. 2(a), (b)). There is a single spectral peak which corresponds to the upper metal interface gravity wave mode ((11) with "+" sign) at
. The resulting motion of the waves generated at both interfaces is stable in this case (figs. 2(a), (b)). There is a single spectral peak which corresponds to the upper metal interface gravity wave mode ((11) with "+" sign) at  . The bottom metal interface oscillates at the same frequency, while the corresponding eigenmode frequency ((11) with "−" sign) is not excited. The laminar damping in this case is sufficient to suppress the instability which would otherwise appear in a purely frictionless case for the battery of square horizontal section
. The bottom metal interface oscillates at the same frequency, while the corresponding eigenmode frequency ((11) with "−" sign) is not excited. The laminar damping in this case is sufficient to suppress the instability which would otherwise appear in a purely frictionless case for the battery of square horizontal section  in the presence of the electric current [12].
in the presence of the electric current [12].
In an intermediate stage of discharge the top layer decreases while the bottom layer increases in thickness. When the metal layers are of the same thicknesses:  , the wave oscillation development is changing, see figs. 2(c), (d). In this case the unstable interfacial motion slowly sets in the upper metal. The Fourier spectrum indicates the instability onset frequency
, the wave oscillation development is changing, see figs. 2(c), (d). In this case the unstable interfacial motion slowly sets in the upper metal. The Fourier spectrum indicates the instability onset frequency  , which is the respective three-layer gravity frequency for the upper metal interface defined by (11) for the present depth values.
, which is the respective three-layer gravity frequency for the upper metal interface defined by (11) for the present depth values.
When the cell is approaching fully discharged state, the lower electrode is thicker than the upper one:  ,
,  . The results shown in figs. 2(e), (f) demonstrate the unstable interfacial motion of the upper metal, which eventually leads to the destabilization of the lower metal interface as well. In this case a complete rupture of the electrolyte, giving the current short-circuit is reached after 1062 seconds. The Fourier spectrum, similarly to the previous example, contains the single low-frequency peak at the corresponding three-layer gravity wave frequency
. The results shown in figs. 2(e), (f) demonstrate the unstable interfacial motion of the upper metal, which eventually leads to the destabilization of the lower metal interface as well. In this case a complete rupture of the electrolyte, giving the current short-circuit is reached after 1062 seconds. The Fourier spectrum, similarly to the previous example, contains the single low-frequency peak at the corresponding three-layer gravity wave frequency  (11). The oscillation of the lower metal is exactly at the same frequency.
(11). The oscillation of the lower metal is exactly at the same frequency.
From these results it can be concluded that the interfacial motion becomes unstable when the cell approaches the discharged state. These results demonstrate also that the instability is developing on the upper metal interface. This agrees with findings in [9] where the condition for the upper interface dominant role was quantified as  . In our case at
. In our case at  ,
,  :
:  .
.
The square-section cell is particularly sensitive to the magnetic interaction, as noted in [10], where the instability onset was characterised by the parameter: ![${\Pi }={j_{0}B_{z}L_{x}L_{y}}/ ([ \rho_{2}-\rho_{3}]h_{02}h_{03}g )$](https://content.cld.iop.org/journals/0295-5075/124/2/24001/revision1/epl19374ieqn80.gif) . For the square cell the inviscid instability threshold was found at
. For the square cell the inviscid instability threshold was found at  . The results in fig. 2 show that the viscous friction is the crucial factor between the stable and unstable states even for the critical square-section cell.
. The results in fig. 2 show that the viscous friction is the crucial factor between the stable and unstable states even for the critical square-section cell.
The role of the hydrodynamic coupling between the top and bottom interfaces can be further analysed if assuming that the bottom interface is fixed as  at all time steps while the electric current is computed for all three layers according to (20), (21). The results for the nearly fully discharged battery (
at all time steps while the electric current is computed for all three layers according to (20), (21). The results for the nearly fully discharged battery ( ,
,  ) are presented in fig. 3. In this case, when the hydrodynamic coupling is neglected, the instability growth rate is even higher than in the coupled case (compare to fig. 2(e)). The respective Fourier spectra (fig. 2(f) and fig. 3(b)), give different frequency values for the oscillation at which the instability sets in. The three-layer frequency (
) are presented in fig. 3. In this case, when the hydrodynamic coupling is neglected, the instability growth rate is even higher than in the coupled case (compare to fig. 2(e)). The respective Fourier spectra (fig. 2(f) and fig. 3(b)), give different frequency values for the oscillation at which the instability sets in. The three-layer frequency ( ) is lower than the corresponding two-layer frequency (
) is lower than the corresponding two-layer frequency ( ).
).
Fig. 3: (Colour online) The top interface instability onset when  ,
,  for the uncoupled wave motion case: (a) H2(0, 0, t) and
for the uncoupled wave motion case: (a) H2(0, 0, t) and  , (b) power spectra and the gravity frequencies.
, (b) power spectra and the gravity frequencies.
Download figure:
Standard imageThe role of the different types of initial perturbations can be investigated by introducing a more complex set of the initial wave shapes defined as  at the upper metal interface. The numerical results are shown in fig. 4, which can be compared to figs. 2(e), (f) for the single-mode perturbation. When the complex perturbation is applied, the growth of the oscillation amplitude is considerably slower compared to the case with the single-mode perturbation at the critical frequency. However the unstable wave frequencies in both cases are exactly the same (
at the upper metal interface. The numerical results are shown in fig. 4, which can be compared to figs. 2(e), (f) for the single-mode perturbation. When the complex perturbation is applied, the growth of the oscillation amplitude is considerably slower compared to the case with the single-mode perturbation at the critical frequency. However the unstable wave frequencies in both cases are exactly the same ( ). A similar outcome was observed when the lower metal interface perturbation is additionally included. These findings indicate that regardless of the initial condition combination the instability sets in at the critical frequency determined by the upper metal interface.
). A similar outcome was observed when the lower metal interface perturbation is additionally included. These findings indicate that regardless of the initial condition combination the instability sets in at the critical frequency determined by the upper metal interface.
Fig. 4: (Colour online) The effect of the initial perturbation of multiple modes on the instability onset when  ,
,  .
.
Download figure:
Standard imageThe unstable interfacial motion is illustrated in fig. 5 at consecutive time increments of a quarter of the period. It can be seen that the instability is in the form of a rotating wave along the cell perimeter. The top and bottom interfaces move in opposite phases. This observation is similar to results in [11]. Figure 6 shows the electric current distribution at the time moment when the interfaces are in the position shown in fig. 5(c). It can be seen that the horizontal current flow in both layers is in opposite directions (fig. 6(a), (b)), and the vertical current jz distribution in the electrolyte layer correlates mostly with the upper interface due to its more pronounced deformation.
Fig. 5: (Colour online) The rotating wave unstable interfacial motion when  ,
,  : (a)
: (a)  ; (b)
; (b)  ; (c)
; (c)  .
.
Download figure:
Standard imageFig. 6: (Colour online) The electric current distribution at  for the interface shown in fig. 5(c): (a) bottom metal, (b) top metal, (c) electrolyte layer.
for the interface shown in fig. 5(c): (a) bottom metal, (b) top metal, (c) electrolyte layer.
Download figure:
Standard imageConclusions
The liquid metal battery of 20 cm size with sodium metal anode, which is a candidate for experimental and commercial implementation, is stable to magneto-hydrodynamic waves for certain combination of the liquid layer depths and becomes unstable at the discharge state when the top metal layer depth is reduced below a critical level. The instability does not depend on the initial interface perturbation type. It was found that when the system is close to the critical discharge state when the top metal depth is reduced to approximately 3.5 cm (equal to the bottom metal depth) it will experience the rotating wave instability unless the metal depth reduction is strictly controlled.










