Abstract
The consequences of imposing boundary conditions to extra spacetime coordinates on a gauge field theory are considered. In a toy model, a larger spacetime symmetry described by a Lorentz-Poincaré SO(p, q) group is broken to a symmetry group of the form 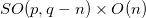 due to boundary conditions in the extra dimensions, leading to an effectively massive gauge field coupled to a "scalar" field in the observable spacetime coordinates.
due to boundary conditions in the extra dimensions, leading to an effectively massive gauge field coupled to a "scalar" field in the observable spacetime coordinates.
Export citation and abstract BibTeX RIS
Introduction
Nowadays, the paradigm of a quantum field theory is invariance under gauge symmetries [1–3]. The necessary condition in order to preserve such invariance is that the gauge fields must remain massless. However, there are physical theories in which a massless gauge field becomes effectively massive by means of some symmetry breaking mechanism. The best known example of this sort is the gauge theory of electroweak interactions, chiefly developed by Weinberg, Salam and Glashow (WSG) [4–6]. In the WSG electroweak theory some of the gauge fields turn out to be massive through a phenomenon known as spontaneous symmetry breaking, originally proposed by Nambu [7] and Goldstone [8], and promptly extended to a gauge theory by Higgs [9], Englert and Brout [10]. The starting point of the electroweak theory is a Dirac Lagrangian for massless fermions, namely, the electron and neutrino fields, which is made invariant under local gauge symmetries through the inclusion of massless gauge fields [2,3]. The introduction of a scalar "Higgs" field, which interacts with the other fields, allows for electrons,  and Z bosons to pick up masses, while photons and neutrinos remain massless. The announcement of the Higgs boson experimental discovery in 2013 [11] can be considered as the culmination of the WSG theory.
and Z bosons to pick up masses, while photons and neutrinos remain massless. The announcement of the Higgs boson experimental discovery in 2013 [11] can be considered as the culmination of the WSG theory.
Despite the enormous success of the Higgs mechanism in explaining the emergence of mass in quantum field theories, there is a distinct way by which gauge fields may become massive. It is the existence of boundary conditions on some hidden spacetime coordinates. Such mechanism can be relevant in describing elementary particle physics at higher energies unaccessible to present-day technology, or to emergent phenomena in condensed matter.
The aim of the present contribution is to discuss the mass generation originated from the breaking of the larger spacetime symmetry group SO(p, q) to a subgroup  , by subjecting some hidden coordinates to boundary conditions. To understand the main differences between the symmetry breaking mechanisms, in the next section a brief discussion of the Higgs phenomenon is posed. The remaining sections are devoted to the consequences of boundary conditions in extra spacetime coordinates.
, by subjecting some hidden coordinates to boundary conditions. To understand the main differences between the symmetry breaking mechanisms, in the next section a brief discussion of the Higgs phenomenon is posed. The remaining sections are devoted to the consequences of boundary conditions in extra spacetime coordinates.
The HIGGS phenomenon
As mentioned previously, many successful quantum field theories handle the mass problem by means of the so-called Higgs mechanism. For the sake of simplicity, we start by considering the Lagrangian density of a charged scalar field ϕ in d-dimensional spacetime,

with 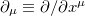 and
and 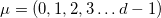 . The invariance of (1) under a gauge transformation of the form
. The invariance of (1) under a gauge transformation of the form ![$\phi^\prime = \exp[i \Lambda(x)] \phi$](https://content.cld.iop.org/journals/0295-5075/125/3/31001/revision1/epl19549ieqn8.gif) , where
, where 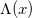 is a scalar spacetime function, is achieved replacing the ordinary derivatives
is a scalar spacetime function, is achieved replacing the ordinary derivatives 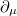 by their covariant form,
by their covariant form, 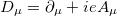 , being
, being 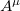 an Abelian gauge field. This procedure leads to
an Abelian gauge field. This procedure leads to

where the term 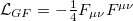 , introduced by hand, is the free Lagrangian density of the gauge field
, introduced by hand, is the free Lagrangian density of the gauge field 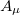 , with the tensor
, with the tensor 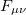 given by the expression
given by the expression 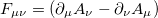 . It is easy to show that the tensor
. It is easy to show that the tensor  satisfies Maxwell's equations,
satisfies Maxwell's equations, 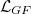 and
and 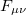 are invariant under the gauge transformation
are invariant under the gauge transformation 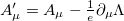 .
.
Now we turn our attention to the field ϕ, remembering that the vacuum of such field must correspond to the state of minimal energy. To find it we minimize the potential energy 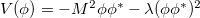 in (2), which leads to two distinct situations, according to the sign of the parameter M2: i) if M2 > 0 the vacuum of the field ϕ is non-degenerate and corresponds to
in (2), which leads to two distinct situations, according to the sign of the parameter M2: i) if M2 > 0 the vacuum of the field ϕ is non-degenerate and corresponds to  ; ii) if M2 < 0, the vacuum of the ϕ-field will be degenerate, corresponding to
; ii) if M2 < 0, the vacuum of the ϕ-field will be degenerate, corresponding to 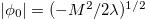 [3]. While the former just corresponds to a massive scalar field of mass M the later has some striking consequences. To understand what actually happens when M2 < 0, let us expand the field ϕ around one of its vacuum states, i.e.,
[3]. While the former just corresponds to a massive scalar field of mass M the later has some striking consequences. To understand what actually happens when M2 < 0, let us expand the field ϕ around one of its vacuum states, i.e.,

with 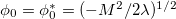 . After the substitution of (3) into (2) and a "rotation" in ϕ to eliminate the variable
. After the substitution of (3) into (2) and a "rotation" in ϕ to eliminate the variable 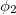 we find
we find

with 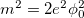 . Now the Lagrangian density (4) describes two massive fields: a scalar field
. Now the Lagrangian density (4) describes two massive fields: a scalar field  and the "photon" field
and the "photon" field 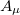 . The mass of the field
. The mass of the field 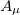 would be determined experimentally. As a matter of fact, we may conclude that the photon described by the Abelian field
would be determined experimentally. As a matter of fact, we may conclude that the photon described by the Abelian field 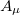 picks up mass from its interaction with the scalar field ϕ, actually the vacuum expectation value of the field ϕ. This phenomenon is known as the Higgs mechanism. Once a well-defined vacuum state from the infinite possibilities is chosen for the field ϕ, its interaction with the field
picks up mass from its interaction with the scalar field ϕ, actually the vacuum expectation value of the field ϕ. This phenomenon is known as the Higgs mechanism. Once a well-defined vacuum state from the infinite possibilities is chosen for the field ϕ, its interaction with the field 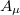 destroys gauge invariance, consequently leaving the photon field massive. An example of this kind of theory we cite the Ginzburg-Landau theory of superconductivity [2,7,8], in which the photon acquires mass and can be better explained in terms of the Higgs phenomenon, as discussed in ref. [3].
destroys gauge invariance, consequently leaving the photon field massive. An example of this kind of theory we cite the Ginzburg-Landau theory of superconductivity [2,7,8], in which the photon acquires mass and can be better explained in terms of the Higgs phenomenon, as discussed in ref. [3].
From the viewpoint of a pure gauge field theory, i.e., considering that from the start there is only a massless gauge field 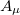 obeying homogeneous Maxwell's equations, one may argue that to give this field a mass it is necessary to introduce a scalar field ϕ possessing degenerate vacuum states and an interaction with the field
obeying homogeneous Maxwell's equations, one may argue that to give this field a mass it is necessary to introduce a scalar field ϕ possessing degenerate vacuum states and an interaction with the field 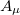 . Once the scalar field had chosen a preferred vacuum state, the field
. Once the scalar field had chosen a preferred vacuum state, the field 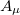 picks up mass at the cost of breaking the gauge invariance. The quantization of the field ϕ leads to the so-called scalar Higgs bosons. Scalar particles possessing the physical properties required to be a Higgs boson were experimentally discovered recently, as mentioned above [11]. In the next section we analyze a different mechanism, which may be called spacetime symmetry breaking, also ending up with a massive field.
picks up mass at the cost of breaking the gauge invariance. The quantization of the field ϕ leads to the so-called scalar Higgs bosons. Scalar particles possessing the physical properties required to be a Higgs boson were experimentally discovered recently, as mentioned above [11]. In the next section we analyze a different mechanism, which may be called spacetime symmetry breaking, also ending up with a massive field.
Spacetime symmetry breaking and boundary conditions
It is well known from differential geometry that in d-dimensional spacetime it is possible to construct a gauge-invariant totally antisymmetric second rank tensor field 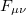 out from a vector
out from a vector 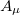 , as follows:
, as follows:

being 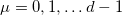 . The "electromagnetic" field
. The "electromagnetic" field  automatically satisfies the following Maxwell's equations:
automatically satisfies the following Maxwell's equations:
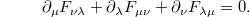
In the context of the Lagrangian formalism, the remaining homogeneous Maxwell's equations,
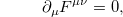
can be obtained from the following gauge-invariant Lagrangian density:

which we assume to be invariant under a spacetime symmetry group denoted by SO(p, q), where 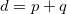 is the total number of spacetime dimensions, being p and q the number of time-like and space-like dimensions, respectively. For instance, in four-dimensional spacetime the above Lagrangian is invariant under the Lorentz group SO(1, 3). Now, let us admit that the spacetime symmetry group SO(p, q) is broken to a subgroup of the form
is the total number of spacetime dimensions, being p and q the number of time-like and space-like dimensions, respectively. For instance, in four-dimensional spacetime the above Lagrangian is invariant under the Lorentz group SO(1, 3). Now, let us admit that the spacetime symmetry group SO(p, q) is broken to a subgroup of the form 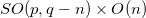 , due to the existence of boundary conditions. From now on, we take the convention that the mathematical symbol used for the observable spacetime coordinates and field components in the observable spacetime having symmetry
, due to the existence of boundary conditions. From now on, we take the convention that the mathematical symbol used for the observable spacetime coordinates and field components in the observable spacetime having symmetry 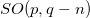 will be kept the same as the original variables, but for the hidden spacetime coordinates or field componentes in the hidden dimensions, corresponding to the O(n) part of the
will be kept the same as the original variables, but for the hidden spacetime coordinates or field componentes in the hidden dimensions, corresponding to the O(n) part of the 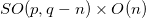 symmetry group, new variables will be introduced. Greek indices will be reserved to the full spacetime or the observable spacetime components, while Latin indices will refer to hidden components. Assuming that the observable spacetime coordinates are restricted to that ones pertaining to the subgroup
symmetry group, new variables will be introduced. Greek indices will be reserved to the full spacetime or the observable spacetime components, while Latin indices will refer to hidden components. Assuming that the observable spacetime coordinates are restricted to that ones pertaining to the subgroup 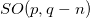 , we may split the full spacetime coordinate variables
, we may split the full spacetime coordinate variables 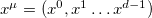 into observable coordinates
into observable coordinates 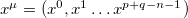 and hidden coordinates
and hidden coordinates  , subjected to
, subjected to 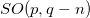 and O(n) symmetry groups, respectively. This way, the ordinary derivatives
and O(n) symmetry groups, respectively. This way, the ordinary derivatives 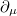 can be splitted as
can be splitted as 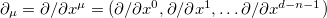 ,
, 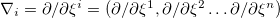 , and the field
, and the field 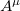 break up to
break up to 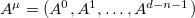 and
and 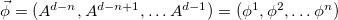 . The procedure used here is analogous to the transverse-longitudinal decomposition used in the study of electromagnetic waveguides [12]. The Lagrangian (6) in terms of the redefined variables is written explicitly below:
. The procedure used here is analogous to the transverse-longitudinal decomposition used in the study of electromagnetic waveguides [12]. The Lagrangian (6) in terms of the redefined variables is written explicitly below:

The reader must remember that now the Greek indices 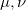 run from 0 to
run from 0 to 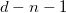 , while the Latin indices i, j run from 1 to n. As we mentioned previously, if the variables
, while the Latin indices i, j run from 1 to n. As we mentioned previously, if the variables 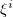 are not actually observable we can integrate them out to obtain an effective Lagrangian density, depending only in the spacetime
are not actually observable we can integrate them out to obtain an effective Lagrangian density, depending only in the spacetime 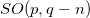 . The desired result is given below:
. The desired result is given below:
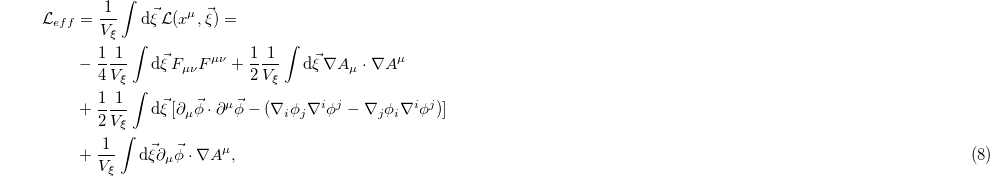
being 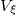 the volume of the hidden variables space. Looking at the above expression, it is convenient to apply the identity
the volume of the hidden variables space. Looking at the above expression, it is convenient to apply the identity 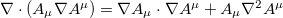 followed by the Gauss theorem to obtain the expression below:
followed by the Gauss theorem to obtain the expression below:
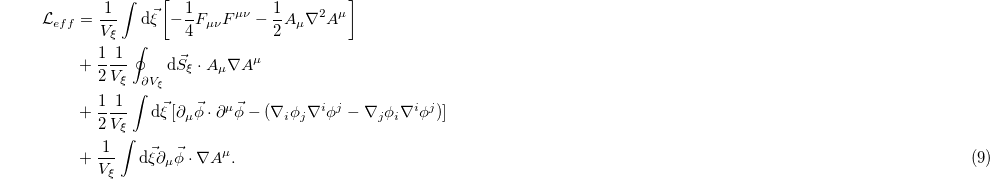
In the above expression  corresponds to the boundary of the volume
corresponds to the boundary of the volume  . Now we will deal with the closed "hypersurface" integral (the term
. Now we will deal with the closed "hypersurface" integral (the term 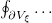 in the above expression), which depends on the value of the fields and its derivatives at the boundary of the volume
in the above expression), which depends on the value of the fields and its derivatives at the boundary of the volume 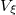 . There are general boundary conditions which can be imposed on the variables ξ but, for the sake of simplicity, we restrict our attention to two possibilities: i) the Neumann condition, where
. There are general boundary conditions which can be imposed on the variables ξ but, for the sake of simplicity, we restrict our attention to two possibilities: i) the Neumann condition, where 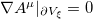 , and ii) the Dirichlet condition where
, and ii) the Dirichlet condition where 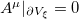 . In both cases the integral over the boundary vanishes and we suppose that
. In both cases the integral over the boundary vanishes and we suppose that

which leads to
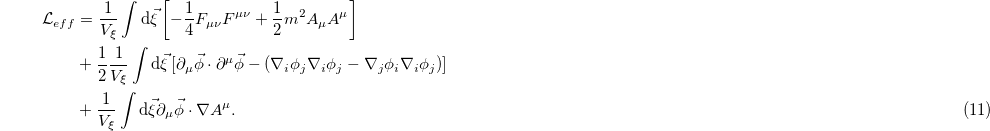
In order to eliminate the dependence of the effective Lagrangian density on the variables 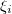 we assume it is possible to write the fields in the following way:
we assume it is possible to write the fields in the following way:


with the normalization conditions below
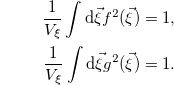
Substitution of the above relations into eq. (11) leads to

Going one step ahead, we define the effective mass matrix Mij and the charges qj:
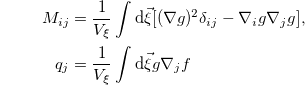
to put (14) into its final and elegant form:

The above Lagrangian describes a massive "photon" field 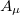 , also known as a Proca field and a "scalar" field
, also known as a Proca field and a "scalar" field 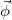 and their interactions in a spacetime group
and their interactions in a spacetime group 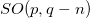 , which is a subgroup of the larger group SO(p, q). The "scalar" field
, which is a subgroup of the larger group SO(p, q). The "scalar" field 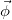 has internal degrees of freedom corresponding to rotations in the subspace O(n) which leaves the effective Lagrangian invariant. One must remember that a scalar field in a quantum field theory is one which transforms as a scalar under rotations in the observed spacetime, i.e., there are no rotation of componentes (only of the observable spacetime coordinates) when a transformation of the spacetime coordinates is performed. The hidden spacetime can be interpreted as an internal space by the observer living in the observable spacetime subjected to the
has internal degrees of freedom corresponding to rotations in the subspace O(n) which leaves the effective Lagrangian invariant. One must remember that a scalar field in a quantum field theory is one which transforms as a scalar under rotations in the observed spacetime, i.e., there are no rotation of componentes (only of the observable spacetime coordinates) when a transformation of the spacetime coordinates is performed. The hidden spacetime can be interpreted as an internal space by the observer living in the observable spacetime subjected to the 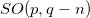 symmetry group.
symmetry group.
To summarize what we have done, notice that our starting point was the free Lagrangian density of a massless gauge field 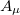 in d-dimensions, subjected to a larger spacetime symmetry group SO(p, q). When the spacetime symmetry is broken to a subgroup
in d-dimensions, subjected to a larger spacetime symmetry group SO(p, q). When the spacetime symmetry is broken to a subgroup 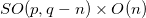 and the only directly observable spacetime coordinates are those coordinates
and the only directly observable spacetime coordinates are those coordinates 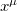 pertaining to the subspace of the symmetry group
pertaining to the subspace of the symmetry group 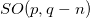 we are led to the effective Lagrangian density (14) in which the components of the gauge field
we are led to the effective Lagrangian density (14) in which the components of the gauge field 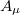 along observable spacetime directions become massive, with mass
along observable spacetime directions become massive, with mass  . The components of the original gauge field denoted by
. The components of the original gauge field denoted by 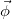 appear to be a scalar field in the observable spacetime, which interacts with the observable field. An observer which can access only the observable spacetime
appear to be a scalar field in the observable spacetime, which interacts with the observable field. An observer which can access only the observable spacetime 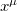 coordinates will attribute the "rotation" degrees of freedom of the field
coordinates will attribute the "rotation" degrees of freedom of the field 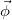 in the subspace
in the subspace 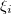 to internal symmetries.
to internal symmetries.
In the next section we will consider the example of the electromagnetic field inside a parallel plate waveguide, illustrating in a pedagogical manner the main results and conclusions established here.
The example of the photon field in a parallel plate waveguide
A parallel plate waveguide is a simple structure by two perfectly conducting planes at z = 0 and z = L. It is well known that the components of the electric-field tangential to a perfect conductor must vanish. It is easy to see that in the case in which the tangential components of the electric field at the conducting planes z = 0 and z = L are 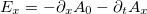 and
and 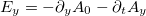 . We can break the SO(1, 3) four-dimensional spacetime
. We can break the SO(1, 3) four-dimensional spacetime 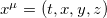 into
into 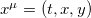 having a symmetry group SO(1, 2) and
having a symmetry group SO(1, 2) and 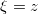 , with corresponding split of the field
, with corresponding split of the field  into two parts,
into two parts, 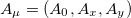 and
and  . Clearly the Dirichlet boundary conditions are satisfied if we put
. Clearly the Dirichlet boundary conditions are satisfied if we put

with
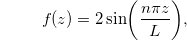
being n any integer number, i.e., 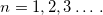 It is straightforward to obtain the mass m which will be given by
It is straightforward to obtain the mass m which will be given by 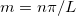 . Notice that the different values of n correspond to particles of different masses. If we do not impose any boundary condition on ϕ we may choose
. Notice that the different values of n correspond to particles of different masses. If we do not impose any boundary condition on ϕ we may choose 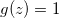 . Following the steps of the previous section we are in the position to obtain the effective electromagnetic Lagrangian, which becomes
. Following the steps of the previous section we are in the position to obtain the effective electromagnetic Lagrangian, which becomes

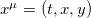 are the "observable" coordinates and z a hidden variable. The mass matrix and charge vanish altogether. In this simple case the above Lagrangian describes a massive field
are the "observable" coordinates and z a hidden variable. The mass matrix and charge vanish altogether. In this simple case the above Lagrangian describes a massive field 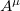 and a non-interacting non-massive "scalar" field ϕ in a spacetime with symmetry group SO(1, 2). An imaginary observer living in this world with only three observable coordinates,
and a non-interacting non-massive "scalar" field ϕ in a spacetime with symmetry group SO(1, 2). An imaginary observer living in this world with only three observable coordinates, 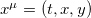 , and without access to the fourth coordinate z subjected to the boundary conditions, will say that the photon field is massive. He also will be tempted to begin with a massless gauge field and introduce a gauge field in such a way that the gauge field ends up with a mass, as explained in a previous section. In a more general situation the field
, and without access to the fourth coordinate z subjected to the boundary conditions, will say that the photon field is massive. He also will be tempted to begin with a massless gauge field and introduce a gauge field in such a way that the gauge field ends up with a mass, as explained in a previous section. In a more general situation the field  would be interpreted as the Higgs field.
would be interpreted as the Higgs field.
Conclusion
In this paper we discussed two alternative ways by which gauge fields may become massive. The first one is the well-known Higgs phenomenon, extensively used in order to describe the electroweak interactions through a gauge theory. The second one attributes the mass of gauge fields to the existence of boundary conditions in hidden dimensions of the spacetime. This way, the mass is not an intrinsic property of the original gauge field but an effective quantity acquired by means of spontaneous breaking ot the spacetime symmetry itself. A simple example was provided by considering the photon field inside a parallel plate waveguide. The Higgs phenomenon naturally leads to the introduction of a scalar field, whose quanta are the so-called Higgs bosons. Based on the above discussion, an alternative interpretation for the Higgs field is that there are hidden dimensions in spacetime, subjected to boundary conditions. The components of the gauge field 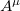 along these extra dimensions form a quantum field
along these extra dimensions form a quantum field 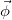 in the observable spacetime, which would be identified as a Higgs field.
in the observable spacetime, which would be identified as a Higgs field.
Acknowledgments
CAD would like to thank the Brazilian agency CNPq for partial financial support through scholarship CNPq 301848/2017-3.





