Abstract
The occurrence of a fundamental length, a lower bound to any output of a position measurement, seems to be an attractive possibility in classical and quantum physics. In this regard, we investigate a simple model in the context of the classical Maxwell-Lorentz theory where a basic length can be identified. We then propose a possible experiment to indirectly detect the existence of this length.
Export citation and abstract BibTeX RIS
Introduction
In physics, a theory is considered satisfactory if we can make appropriate predictions with it. Such predictions entail the measurements of certain observables which are recorded in a system of basic units. This choice of units will be managed primarily by considerations of preference. A considerable insight is presented if we utilize as primary units certain constants of nature. Two usual constants of this kind are the Planck constant and the speed of light in vacuum. As a required "missing" unit we use the centimeter or second. This choice is led by the certitude that the considered theory develops from an inherent relation of quantum physics characterized by ℏ and relativity featured by the constant c. The demand for a theory concerning a fundamental length (time) has been the theme of much surmise in the past and present but it seems correct to say that we are distant from understanding the guise of such a unit in present theories. This reminds us of theories as classical electrodynamics (CED) related to the classical electron radius  , quantum mechanics with length associated to the Compton wavelength
, quantum mechanics with length associated to the Compton wavelength 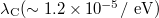 , and string theory: the Planck length
, and string theory: the Planck length 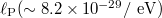 at which established ideas of space-time collapse. There are many situations in physics where it is appropriate to substitute the continuous length (time) parameter with a discrete quantity. Many efforts have been made to build classical and quantum theories founded on this view, such as the ones given in refs. [1–17]. The essential conjecture in some of these theories is that on a quite short time
at which established ideas of space-time collapse. There are many situations in physics where it is appropriate to substitute the continuous length (time) parameter with a discrete quantity. Many efforts have been made to build classical and quantum theories founded on this view, such as the ones given in refs. [1–17]. The essential conjecture in some of these theories is that on a quite short time 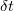 the system does not evolve steadily under unitary evolution but somewhat in a succession of similar transformations. If the time step is negligible, the evolution develops nearly continuously. Phenomenological consequences will depend on the size of
the system does not evolve steadily under unitary evolution but somewhat in a succession of similar transformations. If the time step is negligible, the evolution develops nearly continuously. Phenomenological consequences will depend on the size of  . Therefore, a fundamental length, a lower bound to any output of a position measurement, seems to be an interesting possibility in CED and quantum mechanics as well as in classical and quantum gravity. Exploring the outcomes of a fundamental length scale is one of the best motivated approaches to come into contact with phenomenology, and to acquire knowledge on the essential structure of space-time and the causality principle in physics. Correspondingly, in this article we study an elementary approach in the framework of CED where a fundamental length can be discerned, and then solve some instances in this context. Moreover, we propose an, in principle, simple experiment to measure the occurrence of this length.
. Therefore, a fundamental length, a lower bound to any output of a position measurement, seems to be an interesting possibility in CED and quantum mechanics as well as in classical and quantum gravity. Exploring the outcomes of a fundamental length scale is one of the best motivated approaches to come into contact with phenomenology, and to acquire knowledge on the essential structure of space-time and the causality principle in physics. Correspondingly, in this article we study an elementary approach in the framework of CED where a fundamental length can be discerned, and then solve some instances in this context. Moreover, we propose an, in principle, simple experiment to measure the occurrence of this length.
Fundamental length in CED
To begin with, we recall that in general relativity we have the sequence

where the Riemann curvature tensor is deduced from the Christoffel connection, which in turn, through consecutive first partial derivatives, itself is computed from the metric tensor. By analogy with CED [18,19], i.e., in the framework of a different physical theory, we may ask whether in flat space-time CED it is possible to find a sequence  , where the question mark "?" denotes a hypothetical third-rank tensor deduced from appropriate first-order derivatives of
, where the question mark "?" denotes a hypothetical third-rank tensor deduced from appropriate first-order derivatives of  . As has been already expressed, the electromagnetic four-potential
. As has been already expressed, the electromagnetic four-potential 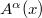 and field-strength tensor
and field-strength tensor  correspond to the metric
correspond to the metric 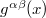 and the connection
and the connection 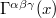 , respectively, in this analogy. We know that the field tensor
, respectively, in this analogy. We know that the field tensor 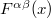 can always be defined in terms of first derivatives of the potential
can always be defined in terms of first derivatives of the potential  through the expression
through the expression

Looking for such possible generalization, note that, to be meaningful, we assume the validity of Maxwell equations, which in a manifestly covariant form are given by

with  , where
, where  is the Levi-Civita pseudo-tensor (we adopt the same notation as Jackson [20]). On the other hand, the Newton-Lorentz equation has been abstracted from a wide reach of electromagnetic phenomena, that is phenomena whose characteristic energy range go from a few eV to GeV-TeV. It is therefore reasonable to ask if its linearity (both in the four-velocity of the particle and in the field tensor) is still valid for this range of energies of current atomic and particle physics experiments, or whether some modification is already required. This modification must naturally arise from the radiative reaction of the accelerated charged particle. To this end, we will consider the (assumed) sequence
is the Levi-Civita pseudo-tensor (we adopt the same notation as Jackson [20]). On the other hand, the Newton-Lorentz equation has been abstracted from a wide reach of electromagnetic phenomena, that is phenomena whose characteristic energy range go from a few eV to GeV-TeV. It is therefore reasonable to ask if its linearity (both in the four-velocity of the particle and in the field tensor) is still valid for this range of energies of current atomic and particle physics experiments, or whether some modification is already required. This modification must naturally arise from the radiative reaction of the accelerated charged particle. To this end, we will consider the (assumed) sequence

where 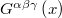 is a tensor of rank three defined below in (6). As one of the simplest, but not trivial, form for this generalization we postulate the nonlinear "Newton-Lorentz equation" [14]
is a tensor of rank three defined below in (6). As one of the simplest, but not trivial, form for this generalization we postulate the nonlinear "Newton-Lorentz equation" [14]

where 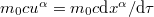 is the four-momentum of the particle, with the basic ansatz
is the four-momentum of the particle, with the basic ansatz

symmetric in the indices βγ, in which

where l0 is regarded as a small basic scalar constant with units of length. Note that in (5) we need to introduce this constant in order to fulfil dimensional homogeneity. As defined here,  is also determined through first derivatives of
is also determined through first derivatives of 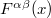 . By using the identity
. By using the identity

we get

Thus,

since 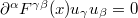 . Note that a proper-time derivative
. Note that a proper-time derivative 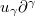 of the field tensor arises, as we would expect. The expression for the generalized Newton-Lorentz equation (10) is thus obtained by means of rather crude arguments. Nevertheless, the new term in this equation satisfies the following properties: It is a covariant perturbation of order l0, i.e., it must be negligible to the usual Newton-Lorentz equation in the appropriate limit
of the field tensor arises, as we would expect. The expression for the generalized Newton-Lorentz equation (10) is thus obtained by means of rather crude arguments. Nevertheless, the new term in this equation satisfies the following properties: It is a covariant perturbation of order l0, i.e., it must be negligible to the usual Newton-Lorentz equation in the appropriate limit 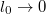 . It is gauge invariant since it is computed only from
. It is gauge invariant since it is computed only from  . It vanishes for a constant electromagnetic field. We recover the Coulomb law for a nearly static (
. It vanishes for a constant electromagnetic field. We recover the Coulomb law for a nearly static ( ) configuration. Furthermore, an external magnetic field can do no work on an isolated charge since
) configuration. Furthermore, an external magnetic field can do no work on an isolated charge since 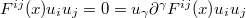 . If we identify
. If we identify  , the term
, the term  could be actually interpreted as a leading (radiation) reaction force on m0 since it is a small correction to the Newton-Lorentz force due to the applied field [21]. Finally, in (10), we have not considered other radiative reaction terms valid when the speed of the particle approaches the speed of light. These terms are nonlinear in the field tensor in the Landau-Lifshitz equation (LLE) [21].
could be actually interpreted as a leading (radiation) reaction force on m0 since it is a small correction to the Newton-Lorentz force due to the applied field [21]. Finally, in (10), we have not considered other radiative reaction terms valid when the speed of the particle approaches the speed of light. These terms are nonlinear in the field tensor in the Landau-Lifshitz equation (LLE) [21].
For simplicity, we will deal with the problem of a charged particle moving in one space dimension, which will facilitate the understanding of the more complex theory in two and three dimensions. So, let us consider a particle of charge e (< 0) and mass m0 moving in a linearly dependent electric field along the z-direction. In this circumstance the equations of motion become (hereafter 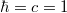 ; see table 1)
; see table 1)

First we choose

with a0 > 0, and  ,
, 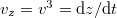 ,
, 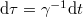 , where
, where 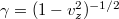 . From (11) we find only two first-order differential equations:
. From (11) we find only two first-order differential equations:


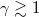 , we obtain the well-known second-order linear differential equation
, we obtain the well-known second-order linear differential equation 
The solution for z(t) is

The amplitude A and phase φ determine the behavior needed to match the initial conditions. This system is in fact the underdamped oscillator: The particle oscillates with the amplitude gradually decreasing to zero.
Table 1:.
Conversion table for natural and MKSA units. Natural units are defined by 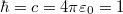 . The remaining units are chosen to be in terms of energy (eV).
. The remaining units are chosen to be in terms of energy (eV).
| Quantity | Symbol | Natural units | MKSA |
|---|---|---|---|
| Energy | eV |  |
 |
| Planck's quantum | ℏ | 1 | 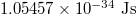 |
| Speed of light | c | 1 | 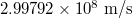 |
| Electron charge | e | 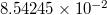 |
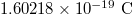 |
| Electron mass | me |  |
 |
| Bohr radius | a0 | 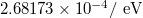 |
 |
| Compton wavelength |  |
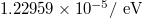 |
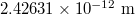 |
| Classical electron radius | 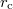 |
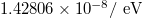 |
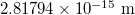 |
| Planck length | 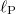 |
 |
 |
On the other hand, in the ultrarelativistic limit, we have that 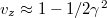 . Now choosing
. Now choosing

we get

The solution for pz(t) becomes

with B (> 0) and C integration constants depending on boundary conditions. This result is of limited interest since higher-order terms in the four-velocity, and quadratic in  , should be included on the right-hand side of (17) for the case of a relativistic particle [21].
, should be included on the right-hand side of (17) for the case of a relativistic particle [21].
An experimentally feasible instance is specified by choosing the electric field as

where  is the Heaviside (step) function, with
is the Heaviside (step) function, with 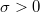 the total surface charge density at z = 0. Here, we choose
the total surface charge density at z = 0. Here, we choose 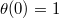 , since θ is mostly used as a distribution. As
, since θ is mostly used as a distribution. As 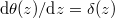 , from (13a) the differential equation for a NR electron, the simplest structureless elementary particle, turns into
, from (13a) the differential equation for a NR electron, the simplest structureless elementary particle, turns into

where we have set 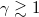 . As shown in fig. 1, let an incident NR electron with momentum
. As shown in fig. 1, let an incident NR electron with momentum 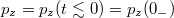 enter into a capacitor from the left with transparent plates made, for instance, of graphene. This material has high electrical conductivity and may be traversed by low-energy electrons [22–25]. Then by integrating in time both sides of (20), we get the momentum transfer to the electron in one space dimension:
enter into a capacitor from the left with transparent plates made, for instance, of graphene. This material has high electrical conductivity and may be traversed by low-energy electrons [22–25]. Then by integrating in time both sides of (20), we get the momentum transfer to the electron in one space dimension:

Fig. 1: Schematic diagram for the one-dimensional electron scattering by the electric field  at z = 0 within a graphene-based capacitor.
at z = 0 within a graphene-based capacitor.
Download figure:
Standard imageIn order to estimate q, we set 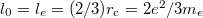 . Thus,
. Thus,

Note that, in this scattering problem, q is larger for a less massive particle, and it does not depend on the incident momentum 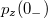 in the NR regime. For instance, consider an incoming NR electron with momentum
in the NR regime. For instance, consider an incoming NR electron with momentum  , corresponding to a kinetic energy of
, corresponding to a kinetic energy of 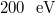 [22,24], and establish an electric-field strength limit
[22,24], and establish an electric-field strength limit 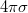 within the plates of the capacitor. Hence, in accordance with table 1, we have that
within the plates of the capacitor. Hence, in accordance with table 1, we have that 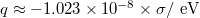 . Currently, graphene capacitors show a high dielectric breakdown electric-field strength of the order of
. Currently, graphene capacitors show a high dielectric breakdown electric-field strength of the order of 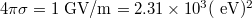 [26]. Thus, under these conditions,
[26]. Thus, under these conditions, 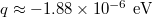 . This seems a fairly small quantity to be measured in laboratory, if we recall that a typical (relativistic) momentum transfer is of the order of MeV-GeV [27]. Finally, we observe that, due to the simplifications made in the description of the systems considered above, they turn out to be described by (approximate) linear differential equations.
. This seems a fairly small quantity to be measured in laboratory, if we recall that a typical (relativistic) momentum transfer is of the order of MeV-GeV [27]. Finally, we observe that, due to the simplifications made in the description of the systems considered above, they turn out to be described by (approximate) linear differential equations.
Conclusion and outlook
Throughout this article, we have considered a series of arguments that could lead to the existence of a fundamental length in CED, a resolution limit in any experiment. Lorentz symmetry and "minimum length" seem to be related to each other since both are expected to be well grounded at low and high energies [11]. So, further research is needed in order to propose an experiment of the sort described, for example, in fig. 1; i.e., improved graphene transparency for specific (low or even high) electron kinetic energies, and stronger electric fields  , so as to confirm our main premises. Hopefully, future studies on graphene-based materials will allow electrons with wide range of kinetic energy to cross (nearly without interaction) graphene sheets, which includes good transparency of dielectric materials (mainly, oxides).
, so as to confirm our main premises. Hopefully, future studies on graphene-based materials will allow electrons with wide range of kinetic energy to cross (nearly without interaction) graphene sheets, which includes good transparency of dielectric materials (mainly, oxides).
It is noteworthy that some authors (see, e.g., refs. [28,29]) assert that 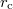 is taken as a minimum possible length scale in nature. This is seemingly contrary to some features of the Standard Model in which the electron is considered a point-like particle whose extension in space vanishes. This constitutes a problem, because they can get infinitely close to each other, with divergent diagrams. At very small distances, one needs to cut the integrals, giving a radius to the particle. We can infer that there may be a more fundamental theory in which electrons are composed of tinier particles called strings. In other words, the electron would in fact have a radius, as do other composite particles. However,
is taken as a minimum possible length scale in nature. This is seemingly contrary to some features of the Standard Model in which the electron is considered a point-like particle whose extension in space vanishes. This constitutes a problem, because they can get infinitely close to each other, with divergent diagrams. At very small distances, one needs to cut the integrals, giving a radius to the particle. We can infer that there may be a more fundamental theory in which electrons are composed of tinier particles called strings. In other words, the electron would in fact have a radius, as do other composite particles. However, 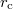 is just about the scale where renormalization becomes significant in quantum electrodynamics (QED). Then, we could be inclined to identify
is just about the scale where renormalization becomes significant in quantum electrodynamics (QED). Then, we could be inclined to identify 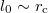 as a fundamental length. Nonetheless, it can be safely said that
as a fundamental length. Nonetheless, it can be safely said that 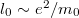 , i.e., l0 is associated with the mass m0 of the interacting particle [21]. Even so, the present classical approach may serve as a guide to estimate the value of le under laboratory conditions, and so decide whether in fact occurs and can be considered as a basic unit of length.
, i.e., l0 is associated with the mass m0 of the interacting particle [21]. Even so, the present classical approach may serve as a guide to estimate the value of le under laboratory conditions, and so decide whether in fact occurs and can be considered as a basic unit of length.
To close, in the above analysis, we have not considered the interesting case where the field-strength tensor depends explicitly on time. In this regard, we are concerned with applications of the LLE in, for instance, laser physics. Presently, there is a controversy about the dynamical behavior of an electron when it is moved by an ultrahigh strength field. Future ultrahigh field facilities [30] will offer lasers with field intensities of the order of 1023–1025 W/cm2 so as to explore the behavior of matter when the electron reaction force surpasses the force due to an applied laser field. This is also of great importance for searching new sources of (coherent) peaks of 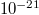 s time period [31,32]. In this physical framework, the opportunity to experimentally probe the LLE may be expected to be available during the coming decade. This equation should work properly when the (electron) radiation reaction force is incidental; nevertheless, when the electron emits radiation with large momentum, the electron recoil can be significant [33]. Alternatives to the LLE, and those arising from QED, can lead to an extensive comparison between the predictions of CED and the classical limit of relativistic QED (see, e.g., refs. [34–37]).
s time period [31,32]. In this physical framework, the opportunity to experimentally probe the LLE may be expected to be available during the coming decade. This equation should work properly when the (electron) radiation reaction force is incidental; nevertheless, when the electron emits radiation with large momentum, the electron recoil can be significant [33]. Alternatives to the LLE, and those arising from QED, can lead to an extensive comparison between the predictions of CED and the classical limit of relativistic QED (see, e.g., refs. [34–37]).
Acknowledgments
This work was supported by Universidad de Los Andes, Santiago, Chile, through grant FAI 12.17.





