Abstract
The generation of relativistic electrons in tokamak plasmas has been the subject of extensive research due to their intrinsic interest as well as the threat they pose to reactor-scale tokamak devices. Runaway electron generation becomes particularly robust for the very large inductive electric fields that are often present during tokamak disruptions. In this letter we show that when such large inductive electric fields are present, the physics of how tokamak geometry impacts runaway generation processes is qualitatively modified compared to the more commonly studied limit of weak inductive electric-field strengths. This modification leads to a significant increase in the efficiency of all runaway generation processes.
Export citation and abstract BibTeX RIS
An important means of generating a relativistic electron population across a range of physical systems corresponds to the runaway mechanism [1–3]. Here a DC electric field in excess of the collisional drag allows electrons to be accelerated to relativistic energies. The term "runaway" originates from the observation that the electric force exerted on an electron is independent of the electron's energy, whereas the collisional drag experienced by that electron decreases as a function of energy. Hence, once an electron exceeds the critical energy where the collisional drag is too weak to brake the electric-field acceleration, it will be accelerated to ever higher energies until a combination of relativistic effects, pitch-angle scattering via Coulomb collisions or high-frequency waves, and radiation eventually arrests the electron's acceleration [4–16].
While the general runaway mechanism is conceptually straightforward, there exist two distinct classes of processes through which electrons may reach sufficient energy to run away. The first class corresponds to local processes in momentum space, whereby electrons are directly accelerated from the bulk electron distribution. Perhaps the best known example of such a local process corresponds to the Dreicer generation [17]. A second, conceptually distinct mechanism is the so-called avalanche amplification mechanism [18–20]. For this latter mechanism thermal electrons undergo large-angle collisions with a pre-existing runaway population. These large-angle collisions, though rare, non-locally scatter thermal electrons to sufficiently high energy to run away. This allows a small initial population of relativistic electrons to grow exponentially in time.
Runaway generation is an issue of particular importance to tokamak plasmas. Specifically, the large currents, and thus the large magnetic-field energy, present in reactor-scale tokamaks are thought to provide a robust means of generating large populations of relativistic electrons [21]. These large relativistic populations pose a significant threat to plasma facing components, and are thus one of the primary challenges faced by the tokamak concept [22]. A key element in assessing the threat posed by runaway electrons is the impact of the magnetic geometry present in a tokamak plasma on runaway generation processes. The conventional understanding of how tokamak geometry impacts runaway electron production is centered on the concept of electron trapping by the tokamak's inhomogeneous magnetic field. In particular, the inhomogeneous magnetic field is capable of trapping electrons on the outboard side of a tokamak via a mechanism analogous to the trapping of a charged particle in the Earth's radiation belt. Such trapped electrons are largely insensitive to the parallel electric field since they are alternatively accelerated/decelerated along subsequent legs of their orbit. Thus, the number of electrons available to be accelerated to relativistic energies is reduced by a factor related to the trapped electron fraction [20]. This is thought to lead to a significant reduction in the efficiency of runaway electron generation in tokamak plasmas, particularly at larger minor radii, where the fraction of trapped electrons can be significant.
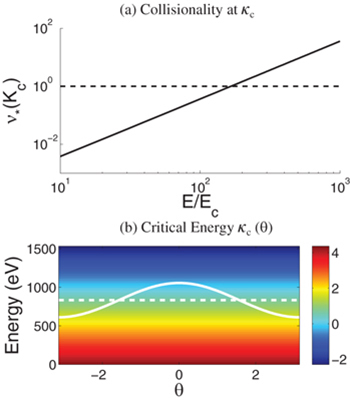
In this letter we show that in the limit of a very strong electric field, runaway electron generation can be more efficient at larger minor radii, in direct contradiction to the conventional picture described above. This striking contrast results from two distinct aspects of runaway electron generation in tokamak plasmas being modified in the large electric-field limit. The first results from the critical energy for runaway acceleration being reduced to a sufficiently low energy such that these electrons are not well characterized by the low collisionality regime. In particular, in a fully ionized plasma the critical energy can be approximated in the non-relativistic limit by 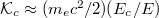 , where
, where  is the electron's kinetic energy, γ is the Lorentz factor, E the parallel electric field, and Ec is the Connor-Hastie electric field [23]. The collisionality at these energies can be quantified by
is the electron's kinetic energy, γ is the Lorentz factor, E the parallel electric field, and Ec is the Connor-Hastie electric field [23]. The collisionality at these energies can be quantified by 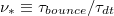 , where
, where 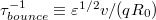 is the bounce time of an electron, and
is the bounce time of an electron, and  is the detrapping time [24]. Here, R0 is the major radius, q is the safety factor,
is the detrapping time [24]. Here, R0 is the major radius, q is the safety factor,  is the inverse aspect ratio, r is the minor radius, and
is the inverse aspect ratio, r is the minor radius, and 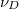 is the pitch-angle scattering rate. As made evident in fig. 1(a), this quantity becomes of order unity or larger for electric fields of several hundred times Ec. Further noting that for an ITER-like scenario with
is the pitch-angle scattering rate. As made evident in fig. 1(a), this quantity becomes of order unity or larger for electric fields of several hundred times Ec. Further noting that for an ITER-like scenario with 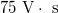 [25] of poloidal flux and a
[25] of poloidal flux and a 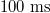 current quench time, this implies an average loop voltage of
current quench time, this implies an average loop voltage of 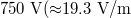 for
for 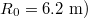 , or roughly 380 times the Connor-Hastie threshold, for a free-electron density of
, or roughly 380 times the Connor-Hastie threshold, for a free-electron density of  , and a Coulomb logarithm of
, and a Coulomb logarithm of 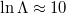 , as is typical of a low-temperature post-thermal quench plasma. Electrons with energy of order
, as is typical of a low-temperature post-thermal quench plasma. Electrons with energy of order  will be in the high-collisionality regime under such conditions. As will be shown explicitly below, such a high-collisionality regime negates the reduction of runaway production due to trapping effects.
will be in the high-collisionality regime under such conditions. As will be shown explicitly below, such a high-collisionality regime negates the reduction of runaway production due to trapping effects.
Fig. 1: (a) Collisionality at critical energy  . The parameters were chosen to be
. The parameters were chosen to be  ,
, 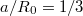 ,
, 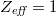 , q = 2,
, q = 2, 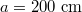 , and
, and 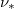 was evaluated at mid radius. (b) Critical energy for an electron to run away (solid white curve) at
was evaluated at mid radius. (b) Critical energy for an electron to run away (solid white curve) at 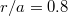 vs. the poloidal angle projected onto a Maxwellian distribution. The dashed white curve indicates the flux surface averaged value. The parameters were chosen to be
vs. the poloidal angle projected onto a Maxwellian distribution. The dashed white curve indicates the flux surface averaged value. The parameters were chosen to be 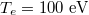 ,
,  , and
, and 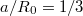 .
.
Download figure:
Standard imageThe second, more subtle effect, results from runaway generation processes becoming strongly localized in the poloidal angle. This physics can be best illustrated by considering the ITER-like scenario discussed above. Under these conditions the average loop voltage is 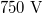 . Hence, in one toroidal transit, an electron can gain up to
. Hence, in one toroidal transit, an electron can gain up to 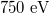 of energy. If we further note that the critical energy for an electron to runaway at this electric field is given by
of energy. If we further note that the critical energy for an electron to runaway at this electric field is given by 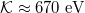 , it is evident that electrons can more than double their energy during a single toroidal transit. Hence, for a plasma with a safety factor
, it is evident that electrons can more than double their energy during a single toroidal transit. Hence, for a plasma with a safety factor 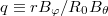 satisfying
satisfying 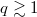 , electrons can be accelerated well in excess of the critical energy
, electrons can be accelerated well in excess of the critical energy 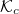 without sampling the entire flux surface. Further noting that the inductive electric field in a tokamak contains a
without sampling the entire flux surface. Further noting that the inductive electric field in a tokamak contains a 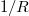 variation [13,26,27] (R is the major radius), runaway electron production can be anticipated to be more efficient on the inboard side compared to the outboard side. As shown below, such localization of runaway generation to a particular poloidal angle can imply a net modification to the overall efficiency of runaway generation. This follows since several runaway generation processes scale nonlinearly with the electric-field strength [17,28,29]. Thus, a local enhancement of runaway production at a given poloidal angle generally will not be balanced by the corresponding reduction at a different poloidal angle. As a heuristic example of this physics, the critical energy
variation [13,26,27] (R is the major radius), runaway electron production can be anticipated to be more efficient on the inboard side compared to the outboard side. As shown below, such localization of runaway generation to a particular poloidal angle can imply a net modification to the overall efficiency of runaway generation. This follows since several runaway generation processes scale nonlinearly with the electric-field strength [17,28,29]. Thus, a local enhancement of runaway production at a given poloidal angle generally will not be balanced by the corresponding reduction at a different poloidal angle. As a heuristic example of this physics, the critical energy 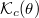 is overlaid onto a Maxwellian distribution in fig. 1(b). It is evident that the critical energy for runaway electron generation penetrates deeper into the thermal electron distribution for
is overlaid onto a Maxwellian distribution in fig. 1(b). It is evident that the critical energy for runaway electron generation penetrates deeper into the thermal electron distribution for 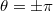 (inboard side). Since the Maxwellian distribution decays exponentially with energy, this deeper penetration is not balanced by the corresponding increase of
(inboard side). Since the Maxwellian distribution decays exponentially with energy, this deeper penetration is not balanced by the corresponding increase of 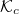 on the outboard side
on the outboard side  . We note in passing, that more complex forms of the parallel electric field can emerge for a range of disruption scenarios. Specifically, considering Ohm's law
. We note in passing, that more complex forms of the parallel electric field can emerge for a range of disruption scenarios. Specifically, considering Ohm's law

where η is the plasma resistivity. Noting that 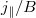 is a flux surface function in a low-β poloidal plasma [24], the parallel electric field will vary like
is a flux surface function in a low-β poloidal plasma [24], the parallel electric field will vary like 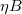 on a flux surface. For the simple case of a constant electron temperature and effective charge
on a flux surface. For the simple case of a constant electron temperature and effective charge 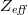 on a flux surface, η will also be constant on a flux surface. The parallel electric field will vary as
on a flux surface, η will also be constant on a flux surface. The parallel electric field will vary as 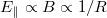 in this limit. This
in this limit. This 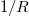 variation of the parallel electric field is not, however, the most general case. In particular, for the case of strongly localized impurity injection,
variation of the parallel electric field is not, however, the most general case. In particular, for the case of strongly localized impurity injection, 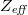 and potentially the electron temperature, will obtain a non-trivial structure on a flux surface, implying a strong poloidal variation of the resistivity. In this limit,
and potentially the electron temperature, will obtain a non-trivial structure on a flux surface, implying a strong poloidal variation of the resistivity. In this limit, 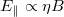 will contain a far more complex dependence on the poloidal angle. In this work we will consider the simplest consistent limit, i.e.,
will contain a far more complex dependence on the poloidal angle. In this work we will consider the simplest consistent limit, i.e., 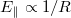 . More complex cases will be considered in a future work.
. More complex cases will be considered in a future work.
The impact of these two processes on runaway generation can be illustrated by considering the runaway probability function (RPF) in a four-dimensional phase space. The RPF is defined as the probability that an electron initialized at a given phase space location is able to run away [30–33]. To make this definition more precise, we will assume an absorbing low-energy boundary condition at the thermal energy, and also neglect all radiation processes. In this way, any electron that reaches the thermal energy will be lost, whereas those that "run away" will be accelerated indefinitely. The form of the evaluated RPF is largely insensitive to the precise choice of the thermal energy as long as it is chosen to be much less than the critical energy to run away. In addition, in order to render spatial transport processes [34,35] and finite orbit width effects irrevelant, all the simulations performed in this letter will be for a large ITER-like device with a minor radius of 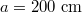 and an exceptionally large toroidal magnetic field
and an exceptionally large toroidal magnetic field 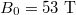 (i.e., tens of times larger than the planned ITER magnetic field). Under these conditions, electrons will be tightly confined to a specific flux surface, allowing runaway generation processes to be evaluated on a flux surface by surface basis. For simplicity, we will also assume uniform temperature, density and a constant loop voltage. First considering the impact to the momentum space structure of the RPF as the system transitions across collisionality regimes, fig. 2 compares the on-axis
(i.e., tens of times larger than the planned ITER magnetic field). Under these conditions, electrons will be tightly confined to a specific flux surface, allowing runaway generation processes to be evaluated on a flux surface by surface basis. For simplicity, we will also assume uniform temperature, density and a constant loop voltage. First considering the impact to the momentum space structure of the RPF as the system transitions across collisionality regimes, fig. 2 compares the on-axis 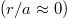 and off-axis
and off-axis 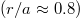 RPFs for both weak and strong inductive electric fields. For the case of a weak inductive electric field, the impact of electron trapping on runaway generation is immediately evident (see figs. 2(a) and (b)). Specifically, while the on-axis RPF is peaked at a pitch of
RPFs for both weak and strong inductive electric fields. For the case of a weak inductive electric field, the impact of electron trapping on runaway generation is immediately evident (see figs. 2(a) and (b)). Specifically, while the on-axis RPF is peaked at a pitch of 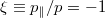 , and decreases monotonically as the pitch is increased, the off-axis case exhibits a local minimum near
, and decreases monotonically as the pitch is increased, the off-axis case exhibits a local minimum near  . The RPF is drastically reduced at this location. Such a reduction in the RPF is a direct result of electron trapping. Turning now to the case of a large inductive electric field
. The RPF is drastically reduced at this location. Such a reduction in the RPF is a direct result of electron trapping. Turning now to the case of a large inductive electric field 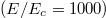 , figs. 2(c) and (d) show the corresponding RPF as a function of energy and pitch. The strong reduction of the RPF inside the trapped region is no longer present. The absence of trapping physics in modifying the RPF at low energies results directly from the high collisionality at these low energies preventing an electron from completing its bounce orbit, thus largely negating the reduction of runaway production due to trapping effects.
, figs. 2(c) and (d) show the corresponding RPF as a function of energy and pitch. The strong reduction of the RPF inside the trapped region is no longer present. The absence of trapping physics in modifying the RPF at low energies results directly from the high collisionality at these low energies preventing an electron from completing its bounce orbit, thus largely negating the reduction of runaway production due to trapping effects.
Fig. 2: Runaway probability functions in momentum space (neglecting radiation damping). Panels (a) and (b) indicate the on 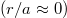 and off
and off 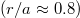 axis cases, respectively, for
axis cases, respectively, for 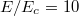 . Panels (c) and (d) indicate the on- and off-axis cases, respectively, for
. Panels (c) and (d) indicate the on- and off-axis cases, respectively, for  . The off-axis cases only contain electrons on the weak-field side, where the trapped-passing boundary is located at approximately
. The off-axis cases only contain electrons on the weak-field side, where the trapped-passing boundary is located at approximately 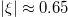 . The other parameters were chosen to be
. The other parameters were chosen to be 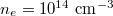 ,
, 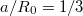 ,
, 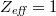 ,
, 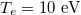 , and a q-profile
, and a q-profile 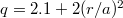 .
.
Download figure:
Standard imageIn addition to modifying the momentum space structure of the RPF, the high-collisionality regime strongly modifies the real space structure of runaway generation processes. Specifically, in the limit of weak collisionality and a modest inductive electric field, the electron distribution can be approximately described in terms of its collisionless invariants 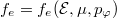 . Here
. Here 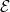 is the electron's energy, μ the magnetic moment, and
is the electron's energy, μ the magnetic moment, and 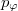 the toroidal canonical momentum. In the limit of small
the toroidal canonical momentum. In the limit of small 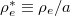 (
(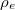 and a are the electron gyroradius and tokamak minor radius, respectively) and neglecting the electrostatic potential, the electron distribution function can be further approximated by
and a are the electron gyroradius and tokamak minor radius, respectively) and neglecting the electrostatic potential, the electron distribution function can be further approximated by  . Here ψ is the poloidal flux function and we have noted that
. Here ψ is the poloidal flux function and we have noted that 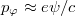 for
for  . In such a limit, the electron distribution function, and thus the RPF, will be a flux surface function for fixed values of γ and μ. This property of the RPF is verified in fig. 3(a) for the case of a weak inductive electric field
. In such a limit, the electron distribution function, and thus the RPF, will be a flux surface function for fixed values of γ and μ. This property of the RPF is verified in fig. 3(a) for the case of a weak inductive electric field 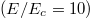 . Here we have constructed the RPF in the
. Here we have constructed the RPF in the  plane for a fixed value of kinetic energy
plane for a fixed value of kinetic energy 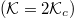 and magnetic moment
and magnetic moment 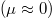 . It is evident that the RPF is constant along the circular flux surfaces assumed in this example, suggesting that runaway generation processes can be described in the three-dimensional space
. It is evident that the RPF is constant along the circular flux surfaces assumed in this example, suggesting that runaway generation processes can be described in the three-dimensional space 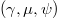 . Contrasting this case with that of a large inductive electric field (see fig. 3(b)), the RPF in this latter case exhibits a strong in-out asymmetry, along with a weaker up-down asymmetry, and is thus not a flux surface function. The strong peaking of the RPF on the inboard side results from the
. Contrasting this case with that of a large inductive electric field (see fig. 3(b)), the RPF in this latter case exhibits a strong in-out asymmetry, along with a weaker up-down asymmetry, and is thus not a flux surface function. The strong peaking of the RPF on the inboard side results from the  scaling of the inductive electric field, allowing runaway generation processes to be more efficient on the inboard side. The weaker up-down asymmetry results from the helicity of the equilibrium magnetic-field lines, and vanishes in the limit of
scaling of the inductive electric field, allowing runaway generation processes to be more efficient on the inboard side. The weaker up-down asymmetry results from the helicity of the equilibrium magnetic-field lines, and vanishes in the limit of 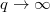 .
.
Fig. 3: Projection of the RPF onto the (R, Z)-plane for electrons with a fixed energy  and
and 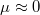 (a narrow range of pitches
(a narrow range of pitches  was included, where
was included, where 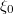 is the electron's pitch on the weak-field side). Only electrons moving in the negative direction were considered. Panel (a) indicates the small-electric-field case
is the electron's pitch on the weak-field side). Only electrons moving in the negative direction were considered. Panel (a) indicates the small-electric-field case 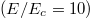 , whereas panel (b) indicates the strong-electric-field case
, whereas panel (b) indicates the strong-electric-field case 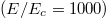 . The other parameters were chosen to be
. The other parameters were chosen to be 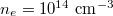 ,
, 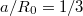 ,
, 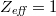 , a q-profile
, a q-profile 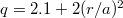 .
.
Download figure:
Standard imageIn order to illustrate the impact of these physical processes on the runaway generation we will use the relativistic drift kinetic solver described in refs. [29,35], which solves for the 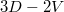 phase-space distribution of runaway electrons incorporating electric-field acceleration, small- and large-angle collisions, as well as synchrotron radiation. This formulation, while computationally more expensive compared to more commonly employed bounce-averaged formulations [20,36–39], does not require the electrons to be in the low-collisionality regime. The two runaway generation processes that we will consider correspond to the Dreicer acceleration and the avalanche amplification of an existing seed electron population. For these calculations we will assume the simplest consistent magnetic geometry, specifically an axisymmetric low-β equilibrium with circular flux surfaces and a constant loop voltage. An ITER-like case with a minor radius of
phase-space distribution of runaway electrons incorporating electric-field acceleration, small- and large-angle collisions, as well as synchrotron radiation. This formulation, while computationally more expensive compared to more commonly employed bounce-averaged formulations [20,36–39], does not require the electrons to be in the low-collisionality regime. The two runaway generation processes that we will consider correspond to the Dreicer acceleration and the avalanche amplification of an existing seed electron population. For these calculations we will assume the simplest consistent magnetic geometry, specifically an axisymmetric low-β equilibrium with circular flux surfaces and a constant loop voltage. An ITER-like case with a minor radius of 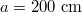 and an inverse aspect ratio of
and an inverse aspect ratio of  is assumed, along with a pure hydrogen plasma with an electron density of
is assumed, along with a pure hydrogen plasma with an electron density of  . The density and temperature will be taken to be constant across the plasma radius. Radiative losses will be neglected in all of the calculations below to facilitate comparisons with previous work.
. The density and temperature will be taken to be constant across the plasma radius. Radiative losses will be neglected in all of the calculations below to facilitate comparisons with previous work.
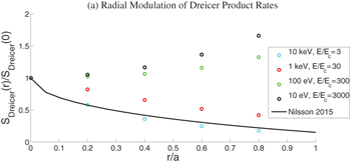
Considering the Dreicer production first, as a means of scanning collisionality regimes, we will compute the Dreicer production rate as a function of the radius for a broad range of temperatures. Noting that the Dreicer electric field ED is related to Ec by 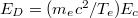 , varying the electron temperature Te while holding
, varying the electron temperature Te while holding 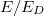 fixed will result in a modulation of
fixed will result in a modulation of 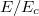 . This modulation will result in the critical energy for runaway electron acceleration to be correspondingly reduced as the temperature is reduced. We note that while this numerical experiment is not intended to model any specific tokamak discharge, the high-temperature cases would be more reminiscent of "quiescent" runaway discharges [40] (though the density here is much higher), whereas the low-temperature cases would be more representative of a disruption. For the highest temperatures considered, the critical energy to run away
. This modulation will result in the critical energy for runaway electron acceleration to be correspondingly reduced as the temperature is reduced. We note that while this numerical experiment is not intended to model any specific tokamak discharge, the high-temperature cases would be more reminiscent of "quiescent" runaway discharges [40] (though the density here is much higher), whereas the low-temperature cases would be more representative of a disruption. For the highest temperatures considered, the critical energy to run away 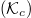 will be located at sufficiently high energy, such that the system will be well characterized by the low-collisionality limit. We thus expect our results to reduce to those of previous calculations [38]. In contrast, for lower temperatures where the collisional time scale is far shorter than the bounce time scale, we anticipate seeing significant discrepancies when compared with existing results. These expectations are borne out in fig. 4. Specifically, for the highest-temperature case considered, the present results agree well with the fit formula given in ref. [38]. For lower temperatures, the predicted Dreicer production rate deviates significantly from existing calculations at finite minor radii. What is perhaps most surprising is that the net production of runaway electrons at large radii has increased significantly compared to its on-axis value. This enhancement of runaway electron generation can be understood by considering the poloidal distribution of newly accelerated electrons. Such a plot is shown in fig. 5. Here the runaway electron population with
will be located at sufficiently high energy, such that the system will be well characterized by the low-collisionality limit. We thus expect our results to reduce to those of previous calculations [38]. In contrast, for lower temperatures where the collisional time scale is far shorter than the bounce time scale, we anticipate seeing significant discrepancies when compared with existing results. These expectations are borne out in fig. 4. Specifically, for the highest-temperature case considered, the present results agree well with the fit formula given in ref. [38]. For lower temperatures, the predicted Dreicer production rate deviates significantly from existing calculations at finite minor radii. What is perhaps most surprising is that the net production of runaway electrons at large radii has increased significantly compared to its on-axis value. This enhancement of runaway electron generation can be understood by considering the poloidal distribution of newly accelerated electrons. Such a plot is shown in fig. 5. Here the runaway electron population with ![$\mathcal{K}\in [\mathcal{K}_c, 4\mathcal{K}_c]$](https://content.cld.iop.org/journals/0295-5075/127/4/45001/revision1/epl19796ieqn95.gif) is shown for both low- and high-temperature cases. For the low-temperature, strong-electric-field case (figs. 5(a) and (b)), the system exhibits a strong in-out asymmetry, with significantly more runaway electrons being produced on the inboard side. This poloidal asymmetry results from the
is shown for both low- and high-temperature cases. For the low-temperature, strong-electric-field case (figs. 5(a) and (b)), the system exhibits a strong in-out asymmetry, with significantly more runaway electrons being produced on the inboard side. This poloidal asymmetry results from the 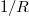 variation of the inductive electric field present in toroidal geometry allowing electrons to be more effectively accelerated on the inboard side. Further, noting that the Dreicer production rate SD is exponentially sensitive to the electric field [23], even a modest modulation of the electric field with poloidal angle can lead to a drastic modification of the runaway production.
variation of the inductive electric field present in toroidal geometry allowing electrons to be more effectively accelerated on the inboard side. Further, noting that the Dreicer production rate SD is exponentially sensitive to the electric field [23], even a modest modulation of the electric field with poloidal angle can lead to a drastic modification of the runaway production.
Fig. 4: Comparison of Dreicer production rates as a function of radius for plasmas at different temperatures. The solid black curve corresponds to the fit formula given in the caption of fig. 6 of ref. [38]. The inductive electric field was chosen to be 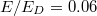 .
.
Download figure:
Standard imageFig. 5: (a) Poloidal cross-section of runaway electrons with an energy between 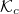 and
and  for a
for a  plasma. (b) Corresponding electron distributions on the inboard and outboard sides. The dashed red line indicates the critical energy
plasma. (b) Corresponding electron distributions on the inboard and outboard sides. The dashed red line indicates the critical energy 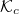 . Panels (c) and (d) give analogous information but for a
. Panels (c) and (d) give analogous information but for a  plasma. For both cases
plasma. For both cases 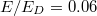 .
.
Download figure:
Standard imageFor the high-temperature, weak-electric-field case (figs. 5(c) and (d)), the in-out asymmetry of runaway generation is substantially smaller. This contrast between the high- and low-temperature cases comes about due to the modest energy gained by an electron in a single toroidal transit. Specifically, the loop voltage in the high-temperature case is several orders of magnitude weaker compared to the low-temperature case. Further, noting that the critical energy  is drastically larger than for the low-temperature case, electrons near
is drastically larger than for the low-temperature case, electrons near 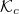 will need to make an extremely large number of toroidal transits before being accelerated well above the critical energy. Thus, an electron in the process of being accelerated will be able to sample the entire flux surface multiple times before significantly exceeding
will need to make an extremely large number of toroidal transits before being accelerated well above the critical energy. Thus, an electron in the process of being accelerated will be able to sample the entire flux surface multiple times before significantly exceeding 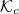 . As a result, electrons near the critical energy
. As a result, electrons near the critical energy 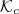 will exhibit minimal asymmetry in the poloidal angle. The modest in-out asymmetry evident in figs. 5(c) and (d) is due to the mirror force slowing passing electrons down on the inboard side, thus resulting in a slightly longer residence time on the strong-field side for these electrons.
will exhibit minimal asymmetry in the poloidal angle. The modest in-out asymmetry evident in figs. 5(c) and (d) is due to the mirror force slowing passing electrons down on the inboard side, thus resulting in a slightly longer residence time on the strong-field side for these electrons.
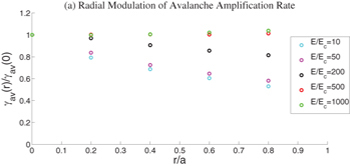
Considering now the case of the avalanche amplification of an initial seed population of runaway electrons 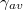 , the radial modulation of this quantity is plotted in fig. 6 as a function of the radius for different electric-field strengths. Here it is evident that for modest values of the electric field, a significant reduction of the avalanche growth rate is observed as a function of radius. In analogy with the case of the Dreicer production, as the electric-field strength is increased the reduction of the rate of avalanche amplification becomes more modest, until asymptoting to a value comparable to its on-axis value. In contrast to the case of the Dreicer production, no significant enhancement in runaway avalanche production is present at large minor radii. This is due to the avalanche amplification mechanism scaling approximately linearly with the inductive electric field, hence the in-out asymmetry in runaway generation largely cancels.
, the radial modulation of this quantity is plotted in fig. 6 as a function of the radius for different electric-field strengths. Here it is evident that for modest values of the electric field, a significant reduction of the avalanche growth rate is observed as a function of radius. In analogy with the case of the Dreicer production, as the electric-field strength is increased the reduction of the rate of avalanche amplification becomes more modest, until asymptoting to a value comparable to its on-axis value. In contrast to the case of the Dreicer production, no significant enhancement in runaway avalanche production is present at large minor radii. This is due to the avalanche amplification mechanism scaling approximately linearly with the inductive electric field, hence the in-out asymmetry in runaway generation largely cancels.
Fig. 6: Comparison of avalanche amplification rates as a function of the radius for different inductive electric fields.
Download figure:
Standard imageThis letter has shown that runaway generation processes exhibit non-trivial structure in the four-dimensional phase space 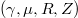 in the limit of large parallel electric fields. As indicated in fig. 3, such modifications lead to a drastic increase in the RPF across the poloidal cross-section of a tokamak plasma implying an increase in the efficiency of all runaway generation processes. This enhancement is verified by explicitly evaluating the efficiency of the Dreicer production and avalanche amplification as a function of the minor radius for a hydrogen plasma. It is found that both processes can be significantly more efficient in the limit of large electric fields for finite minor radii compared to predictions from present models based on the limit of asymptotically small collisionality.
in the limit of large parallel electric fields. As indicated in fig. 3, such modifications lead to a drastic increase in the RPF across the poloidal cross-section of a tokamak plasma implying an increase in the efficiency of all runaway generation processes. This enhancement is verified by explicitly evaluating the efficiency of the Dreicer production and avalanche amplification as a function of the minor radius for a hydrogen plasma. It is found that both processes can be significantly more efficient in the limit of large electric fields for finite minor radii compared to predictions from present models based on the limit of asymptotically small collisionality.
Two readily identifiable uncertainties remain with regard to the application of the above results to disruption modeling. The first concerns the form of the inductive electric field on a flux surface. While the present work has assumed the resistivity to be constant on a flux surface, the presence of a toroidally and poloidally localized impurity source such as a shattered pellet can lead to a strong variation of both the effective charge and electron temperature on a magnetic flux surface. Noting that the parallel electric field varies as 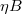 , where
, where  , strong local variations in these two quantities will lead to corresponding variations in the structure of the parallel electric field. As shown in figs. 3 and 4, the structure of the parallel electric field along a field line can significantly modify the net efficiency of runaway seed generation mechanisms such as the Dreicer production in the limit of large inductive electric fields. A careful consideration of this process is thus necessary for understanding the impact of localized impurity injection methods on runaway formation.
, strong local variations in these two quantities will lead to corresponding variations in the structure of the parallel electric field. As shown in figs. 3 and 4, the structure of the parallel electric field along a field line can significantly modify the net efficiency of runaway seed generation mechanisms such as the Dreicer production in the limit of large inductive electric fields. A careful consideration of this process is thus necessary for understanding the impact of localized impurity injection methods on runaway formation.
In addition, the present work has considered the simple case of a hydrogen plasma. The presence of impurities will modify the above picture via two partially compensating effects. The first is that the presence of mid- to high-Z impurities will significantly increase the pitch-angle scattering rate 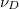 , and thus the effective collisionality
, and thus the effective collisionality 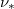 at a given energy. In contrast, for a fixed value of the parallel electric field, the injection of impurities will increase the critical energy to run away. Noting that
at a given energy. In contrast, for a fixed value of the parallel electric field, the injection of impurities will increase the critical energy to run away. Noting that 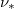 scales inversely with the electron's energy, this will tend to decrease
scales inversely with the electron's energy, this will tend to decrease 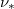 near the critical energy for runaway acceleration, and thus push the system closer to the collisionless regime. The interplay between these two partially offsetting processes will be studied in a future publication.
near the critical energy for runaway acceleration, and thus push the system closer to the collisionless regime. The interplay between these two partially offsetting processes will be studied in a future publication.
Acknowledgments
This work was jointly supported by the Theory Program of Office of Fusion Energy Sciences, and two SciDAC projects on Tokamak Disruption Simulation (TDS) and runaway electrons (SCREAM) by Office of Fusion Energy Science and Office of Advanced Scientific Computing. This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Administration under Contract No. 89233218CNA000001.