Abstract
We use the extended uncertainty principle (EUP) in order to obtain the Rényi entropy for a black hole (BH). The result implies that the non-extensivity parameter, appearing in the Rényi entropy formalism, may be evaluated from the considerations which lead to EUP. It is also shown that, for excited BHs, the Rényi entropy is a function of the BH principal quantum number, i.e., the BH quantum excited state. Temperature and heat capacity of the excited BHs are also investigated addressing two phases while only one of them can be stable. In this situation, whereas entropy is vanishing, temperature may take a non-zero positive minimum value, depending on the value of the non-extensivity parameter. The evaporation time of excited BH has also been studied.
Export citation and abstract BibTeX RIS
Introduction
On the one hand, the uncertainty principle inspires Bekenstein entropy, and indeed, various generalized uncertainty principles (GUP) add different modifications to Bekenstein entropy [1–5]. On the other hand, Bekenstein entropy is a non-extensive entropy measure, a property which motivates some physicists to consider it as a suitable candidate for the Tsallis entropy in calculating the Rényi entropy [6–10]. In fact, due to the long-range nature of gravity [11], the use of a generalized entropy formalisms such as those introduced by Tsallis [12] and Rényi [13] has recently been taken into consideration [6–10,14,15].
A long-range interacting system with W discrete states while each state i has probability Pi may follow a power probability distribution instead of the ordinary distribution [11–13]. Working with 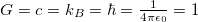 (Planck units), where kB denotes the Boltzmann constant, the Tsallis entropy of such system is defined as [12]
(Planck units), where kB denotes the Boltzmann constant, the Tsallis entropy of such system is defined as [12]

where q is an unknown parameter [11]. It is worthwhile mentioning that one can reach  , where A denotes the horizon of system (boundary), by applying the Tsallis entropy definition (1) to the gravitational systems [16]. This result is in agreement with the cosmological studies in which authors assumed
, where A denotes the horizon of system (boundary), by applying the Tsallis entropy definition (1) to the gravitational systems [16]. This result is in agreement with the cosmological studies in which authors assumed 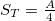 in calculating Rényi entropy [6–10] written as [11]
in calculating Rényi entropy [6–10] written as [11]

in which 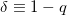 . In addition to the successes of this entropy in describing the cosmos [6–8,10], it can also be combined with Verlinde's hypothesis [17] to give us a theoretical basis for the MOND theory and its modifications [9]. In this paper, we are going to show that EUP can also lead to the emergence of Rényi entropy. In addition, the relation between δ (and thus q) and the quantum-mechanical parameter appearing in EUP is also derived. After getting the mentioned aim in the next section, we study some thermodynamic properties of excited BHs meeting Rényi entropy in the third section. The last section is devoted to summary and concluding remarks.
. In addition to the successes of this entropy in describing the cosmos [6–8,10], it can also be combined with Verlinde's hypothesis [17] to give us a theoretical basis for the MOND theory and its modifications [9]. In this paper, we are going to show that EUP can also lead to the emergence of Rényi entropy. In addition, the relation between δ (and thus q) and the quantum-mechanical parameter appearing in EUP is also derived. After getting the mentioned aim in the next section, we study some thermodynamic properties of excited BHs meeting Rényi entropy in the third section. The last section is devoted to summary and concluding remarks.
From EUP to Rényi entropy
In the framework of high-energy physics, such as quantum gravity, various GUP and EUP are derived [1,18–21], which can generally be written as [18]

Here, γ is positive and depends on the expectation values of p and x [18,22]. Bearing in mind the fact that the minimum uncertainty is obtainable for 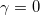 [22], we consider the
[22], we consider the 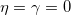 case which leads to EUP written as [1,18–21,23]
case which leads to EUP written as [1,18–21,23]

where β is positive and independent of the values of 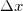 and
and 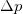 [18]. The non-zero minimal values of
[18]. The non-zero minimal values of 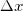 and
and 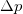 , called
, called 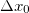 and
and 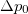 , respectively, are obtainable whenever
, respectively, are obtainable whenever  [18]. The above EUP affects the early-universe thermodynamics [22], and in general, there are deep connections between EUP and GUP and i) the dispersion relation [24,25], ii) the Chandrasekhar and Jeans limits and the dark energy problem [23,26]. More studies on the outcomes of employing GUP in various branches of physics can also be found in [1–5,27–33].
[18]. The above EUP affects the early-universe thermodynamics [22], and in general, there are deep connections between EUP and GUP and i) the dispersion relation [24,25], ii) the Chandrasekhar and Jeans limits and the dark energy problem [23,26]. More studies on the outcomes of employing GUP in various branches of physics can also be found in [1–5,27–33].
Whenever the EUP (4) is valid, one can write 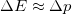 for the uncertainty of the particle energy
for the uncertainty of the particle energy  [3–5,30–32], leading to
[3–5,30–32], leading to

In BH physics, whenever a BH with area A absorbs or emits a quantum particle with energy E and size R, then the changes in the BH area follows the 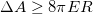 relation [28–30]. Since the size of a quantum particle cannot be less than the uncertainty in its position [29,30,34], one reaches
relation [28–30]. Since the size of a quantum particle cannot be less than the uncertainty in its position [29,30,34], one reaches 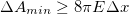 for a quantum particle [5,29,30]. Combining this result with eq. (5), we reach
for a quantum particle [5,29,30]. Combining this result with eq. (5), we reach

As has been argued in refs. [5,28–30], one can write 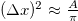 and insert it in eq. (6) to obtain
and insert it in eq. (6) to obtain

where λ is an unknown coefficient fixed later [5].
Therefore,  is the minimum change in the boundary A whenever EUP (4) is valid. It is also obvious to assume that the corresponding entropy change is also minimum and equal to one bit of information
is the minimum change in the boundary A whenever EUP (4) is valid. It is also obvious to assume that the corresponding entropy change is also minimum and equal to one bit of information 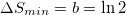 [5,17,34]. The above argument motivates us to write
[5,17,34]. The above argument motivates us to write

leading to

In the limit of 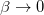 , the Bekenstein entropy
, the Bekenstein entropy 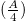 should be recovered [1–5,34,35] which yields
should be recovered [1–5,34,35] which yields

whereby we get

Thus, one can realize that i) EUP may allow us to employ the Rényi entropy, and in this situation, ii) the EUP parameter β determines the value of the non-extensivity parameter δ. Finally, it is also worthwhile mentioning that the value of λ obtained in eq. (10) is the same as that of the previous work by other authors [5] in which the 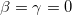 case has been studied.
case has been studied.
Applications to the excited BHs
For excited BHs, i.e., the BHs which emitted a large amount of Hawking quanta, the recent Bohr-like approach to BH quantum physics in [36–38] permits to write the Bekenstein entropy in terms of the BH quantum level as [38]

where M is the original BH mass and n is the BH principal quantum number if the BH is seen as gravitational atom, see, e.g., [36–38]. We indeed recall that, the intuitive but general belief [36–38]: the BHs result in highly excited states representing both the Hydrogen atom and the 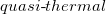 emission in quantum gravity, has been shown to be correct, because the Schwarzschild BH results in somewhat similar to the historical semi-classical hydrogen atom introduced by Bohr in 1913, see [36–38] for more details. Thus, by using eqs. (2) and (11), the Rényi entropy becomes function of the BH principal quantum number, i.e., the BH excited state, given as
emission in quantum gravity, has been shown to be correct, because the Schwarzschild BH results in somewhat similar to the historical semi-classical hydrogen atom introduced by Bohr in 1913, see [36–38] for more details. Thus, by using eqs. (2) and (11), the Rényi entropy becomes function of the BH principal quantum number, i.e., the BH excited state, given as

Accepting the E = M relation and bearing the 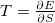 relation in mind, one reaches
relation in mind, one reaches

for temperature of the Hawking radiation in this formalism. As a check, the temperature 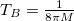 , obtained by using the Bekenstein entropy, is also recovered at the appropriate limit
, obtained by using the Bekenstein entropy, is also recovered at the appropriate limit 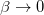 . In this manner, for
. In this manner, for 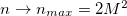 [38], we have
[38], we have 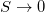 and
and  independent of the value of β. Moreover, the heat capacity evaluated as
independent of the value of β. Moreover, the heat capacity evaluated as

includes a singularity at 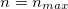 whenever
whenever  . For this critical value of n, we have
. For this critical value of n, we have 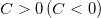 for
for 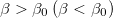 , and in neighboring of this point one can write
, and in neighboring of this point one can write 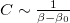 . This means that the
. This means that the 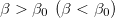 phase can be stable (unstable) [39–41]. For the critical value
phase can be stable (unstable) [39–41]. For the critical value 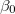 , one can write (14) as
, one can write (14) as

indicating T > TB for n < nmax which means that TB is the minimum possible temperature in this situation. More studies on the non-excited BHs  as well as their thermodynamics in the framework of the Rényi entropy can also be found in [39,42,43].
as well as their thermodynamics in the framework of the Rényi entropy can also be found in [39,42,43].
Now, let us look at the radiation of excited BH as a black-body radiation, and write [40,42]

where σ denotes the Stefan-Boltzman constant, and additionally, we assumed that the 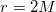 relation is still valid [38]. Therefore, by using eq. (14), the time that a BH needs to lose its mass M can be evaluated as
relation is still valid [38]. Therefore, by using eq. (14), the time that a BH needs to lose its mass M can be evaluated as

leading to

where 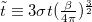 . Whenever
. Whenever 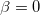 or even
or even 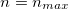 , one obtains
, one obtains

the evaporation time of a Schwarzschild BH [42]. The reason is clear, for both the addressed cases, eq. (14) reduces to the ordinary temperature of the Schwarzschild BH [38]. It is also worthwhile mentioning some similarities and differences between the properties of an excited Schwarzschild BH in the Bekenstein and Rényi entropy formalisms. i) Both the Bekenstein (12) and Rényi (13) entropies vanish for 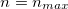 , ii) in the framework of the Bekenstein entropy, temperature is always independent of n, and iii) heat capacity is always negative, independent of the value of n, in the regime of the Bekenstein entropy (the
, ii) in the framework of the Bekenstein entropy, temperature is always independent of n, and iii) heat capacity is always negative, independent of the value of n, in the regime of the Bekenstein entropy (the 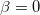 limit of (15)), while C can be positive depending on the values of n and β. For example, whereas
limit of (15)), while C can be positive depending on the values of n and β. For example, whereas 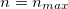 , we have C > 0 if
, we have C > 0 if 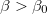 .
.
Summary and concluding remarks
The Rényi entropy for a BH has been obtained through EUP. By using the recent Bohr-like approach to BH quantum physics, we have also shown that, for excited BHs, the Rényi entropy is a function of the BH principal quantum number, i.e., the BH quantum excited state. Some thermodynamic properties of excited BH meeting Rényi entropy have also been addressed. The results show that although there are two phases at 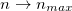 , only the phase with
, only the phase with 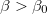 can be stable. Moreover, whenever
can be stable. Moreover, whenever 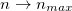 , then entropy vanishes, and temperature takes its non-zero possible minimum value (TB) if
, then entropy vanishes, and temperature takes its non-zero possible minimum value (TB) if 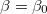 .
.
Evaporation time of the excited BHs has also been studied. Although we addressed the 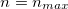 case in our study, in reality, the maximum possible value of n, namely Nmax, may be limited as
case in our study, in reality, the maximum possible value of n, namely Nmax, may be limited as 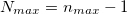 whenever the Planck mass and the Planck distance are approached [38,44]. In this manner, none of the Bekenstein and Rényi entropies vanish when the maximum value of n is taken by the excited BH. This leads to the interesting results in the Rényi entropy framework, in agreement with the third law of thermodynamics, i) based on eq. (13), entropy takes its minimum value which is non-zero, and ii) from eq. (14), the minimum of temperature can be positive or even greater than TB depending on the value of β.
whenever the Planck mass and the Planck distance are approached [38,44]. In this manner, none of the Bekenstein and Rényi entropies vanish when the maximum value of n is taken by the excited BH. This leads to the interesting results in the Rényi entropy framework, in agreement with the third law of thermodynamics, i) based on eq. (13), entropy takes its minimum value which is non-zero, and ii) from eq. (14), the minimum of temperature can be positive or even greater than TB depending on the value of β.
Acknowledgments
The work of HM has been supported financially by Research Institute for Astronomy and Astrophysics of Maragha (RIAAM) under project No. 1/6025–59.





