Abstract
The study of the black holes in higher-dimensional space-time has got the focus mainly after developments of string theory or M-theory. Beside this, construction of brane world scenario also motivates to study the properties of higher-dimensional black holes. In this letter, we calculate the maximal interior volume of higher-dimensional charged black holes which is actually the extension of a previous work (Ong Y. C., Gen. Relativ. Gravit., 47 (2015) 88 (arXiv:gr-qc/1503.08245)) in addition to the study of entropy of the same class of black holes' interior. The actual detail investigation and proof have been shown in Christodoulou M. and Lorenzo T. D., Phys. Rev. D, 94 (2016) 104002 (arXiv:gr-qc/1604.07222). We try in this letter, to establish a generalized form which is not only the maximal interior volume but also the entropy of the black hole in its interior for Schwarzschild like regular black holes. We also show how their behaviors depend on the mass parameter m considering the constant valued horizon and for the charge parameter q = 0 and q > 0.
Export citation and abstract BibTeX RIS
Introduction
Since the idea of black hole's (BH hereafter) volume depends on the choice of space-like hypersurface, it is not well defined in general relativity (GR hereafter). Reference [1] has shown some explicit examples in this regard. The concept of BHs' interior volume is difficult to recognize, as there is no suitable method to choose an appropriate space-like hypersurface in a BH yet. Reference [2] has recently proposed that the volume acts like a space-like surface with spherical nature in the interior of the BH. It is shown that the maximal interior volume V attained by an asymptotically flat Schwarzschild BH having ADM mass M is linearly proportional to advanced time v, such as 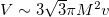 . This means the maximal interior volume grows with advanced time. If Schwarzschild coordinates
. This means the maximal interior volume grows with advanced time. If Schwarzschild coordinates  are considered, the maximal volume reaches the
are considered, the maximal volume reaches the 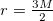 hypersurface, which is again the maximal space-like strip in the interior of Schwarzschild geometry. In the classical limit, the BH remains static from the outside view attaining the same area as
hypersurface, which is again the maximal space-like strip in the interior of Schwarzschild geometry. In the classical limit, the BH remains static from the outside view attaining the same area as 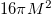 .
.
References [3,4] have extended the above result to the Reissner-Nordström and Kerr BH and derived the formula of the maximal interior volume of the Reissner-Nordström BH which is almost similar to that of the Schwarzschild BH. Interior volume of this article also increases linearly with the advanced time v. For Kerr BH, the interior volume does not necessarily act in accordance to the flat space intuition [4]. For a nonstatic BH such an amount of volumetric maxima is found in refs. [5,6]. Generally, it is not necessary to increase the volume monotonically with the increase of horizon area [7], e.g., i) the maximal interior volume for asymptotically locally AdS BHs having AdS length L with total topology which grows like  , independently of their horizon area; ii) for asymptotically locally AdS BHs in 5D space-time with lens space topology
, independently of their horizon area; ii) for asymptotically locally AdS BHs in 5D space-time with lens space topology 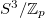 , the maximal interior volume grows like
, the maximal interior volume grows like 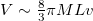 , which shrinks the horizon area to zero at the limit
, which shrinks the horizon area to zero at the limit 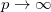 .
.
Two questions mainly motivate us to study BHs' interior volume: i) a BH has nonstatic interior due to the swapping nature of its space and time coordinates; ii) the nature of space-time slices taken in GR, the volume depends on the way space-time is sliced. For a stationary BH, a slicing invariant volume is however found in ref. [8]. A definition of the volume rate for a stationary nondegenerate BH is raised in the article in [9]. The concept of "vector volume" is explained by examining the rate of growth of an invariant volume for some space-time regions along a divergence-free vector field [10]. A spherically symmetric BH's horizon is foliated by space-like spheres 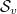 labeled by the symmetric time v and the sphere
labeled by the symmetric time v and the sphere 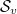 is defined as the one crossed by a light signal sent by a remote stationary observer at position r with proper time
is defined as the one crossed by a light signal sent by a remote stationary observer at position r with proper time 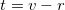 . CR volume is nothing but the maximal volume of the spherically symmetric surface Σ bounded by
. CR volume is nothing but the maximal volume of the spherically symmetric surface Σ bounded by  . Interior volumes grow with time for different kinds of BHs [4,11–13]. Analysis of entropy of massless scalar particles inside the BHs [14,15] may provide us with implications on discussions of the information paradox, since a larger volume can accommodate huger information [16].
. Interior volumes grow with time for different kinds of BHs [4,11–13]. Analysis of entropy of massless scalar particles inside the BHs [14,15] may provide us with implications on discussions of the information paradox, since a larger volume can accommodate huger information [16].
The formulation of maximal interior volume is useful to estimate not only phase space volume but also the horizon entropy of the BHs [4]. When the Hawking radiation is taken into account, such construction of volume has remarkable importance to resolve the information paradox problem [17]. Since the volume is always increasing with advanced time, one will have a large amount of volume to hide this significantly huge information at the end of evaporation [3]. The entropy of the hidden modes in the interior of the BHs [18,19] is one of the important quantities observed in this context. The authors of ref. [14] have studied the entropy for a Schwarzschild BH. The entropy in the interior of a Kerr BH has investigated and a general method to find the entropy within the BH has proposed in ref. [20].
In this letter, we are inspired to study the BHs embedded in higher-dimensional space-time due to the development of string theory, M-theory and brane world scenario. The naive geometric volume, thermodynamic volume, entropy in the exterior of the BHs and the effects of logarithmic correction have been studied in the literature [21,22]. But the interior properties are still not studied deeply. This fact motivates us to concentrate on different properties of the interior volume and entropy in the background of different dimensions.
This letter is organized as follows: in the next section, we will calculate the interior volume of higher-dimensional charged BHs. In the third section, the entropy will be calculated. Finally, we will give a brief discussion and conclude the letter. Throughout this letter, we use the Planck units, i.e., 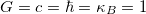 and signature
and signature  .
.
The brief review of thermodynamics of higher-dimensional charged black holes
Authors of ref. [23] have investigated the nature of the low frequency absorption cross section for electromagnetic waves for extreme Reissner-Nordström BHs in higher-dimensions. The case of higher-dimensional collapsing and static thin massive charged dust shells in a Reissner-Nordström BH background is found in refs. [7,24–30].
The higher-dimensional charged BHs metric is expressed as [31]

and 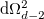 represents the canonical volume associated with eq. (1). The parameters m and q are, respectively, related to the ADM mass M and the electrical charge of the BH Q given in ref. [31] as
represents the canonical volume associated with eq. (1). The parameters m and q are, respectively, related to the ADM mass M and the electrical charge of the BH Q given in ref. [31] as

with the volume of the unit d-sphere, 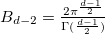 . On the event horizon
. On the event horizon ![${r= r_h=\bigg[\frac{m}{2} + \frac{\sqrt{m^2-4q^2}}{2}\bigg]^{\frac{1}{d-3}}}$](https://content.cld.iop.org/journals/0295-5075/128/3/30007/revision1/epl19912ieqn17.gif) , the mass parameter m can be expressed as
, the mass parameter m can be expressed as

The BH metric given in eq. (1), while written in Eddington-Finkelstein coordinates 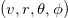 , takes the form
, takes the form

where v is the "advanced time" related to the Schwarzschild coordinates 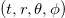 as
as
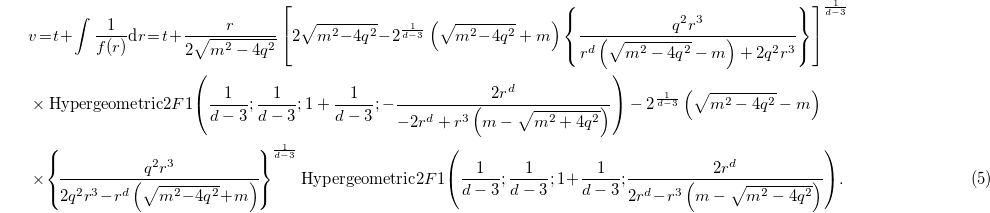
The maximal volume inside the BH is [12] given by

where m and q are both the functions of advanced time v. This maximal volume (6) corresponds to the hypersurface having radius given as

Since 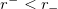 , we consider the positive root. Here
, we consider the positive root. Here ![${r_{-}\bigg(= \bigg[ \frac{m}{2} - \frac{\sqrt{m^2-4q^2}}{2}\bigg]^{\frac{1}{d-3}}\bigg)}$](https://content.cld.iop.org/journals/0295-5075/128/3/30007/revision1/epl19912ieqn21.gif) denotes the inner horizon of the BH. The variation of maximal volume inside the BH V with respect to the advanced time v calculated as
denotes the inner horizon of the BH. The variation of maximal volume inside the BH V with respect to the advanced time v calculated as

This is always non-negative. This means the interior volume is always increasing even if the mass of the BH is decreasing. If m and q be considered as constant parameters, as classical general relativity without Hawking radiation, then the maximal volume becomes

In the limit 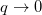 and for d = 4, the result approaches to the largest interior volume contained within the event horizon of an asymptotically flat Schwarzschild BH which is shown in the appendix. Increment in dimension increases the degrees of freedom. This again prefers the formation of a naked singularity rather than a BH for which a part of space-time should be wrapped by a singularity known as the event horizon. Actually, more the dimension we have, more free we are to overcome a space-time wrap. Now when it is likely to have naked singularities rather than a BH we may take it as an incident where the event horizon is very small or turning infinitely small with the increment of d. This is found in figs. 1(a) and (b), where we see the rate increment of interior volume with advanced time reduces down abruptly if the dimension is increased.
and for d = 4, the result approaches to the largest interior volume contained within the event horizon of an asymptotically flat Schwarzschild BH which is shown in the appendix. Increment in dimension increases the degrees of freedom. This again prefers the formation of a naked singularity rather than a BH for which a part of space-time should be wrapped by a singularity known as the event horizon. Actually, more the dimension we have, more free we are to overcome a space-time wrap. Now when it is likely to have naked singularities rather than a BH we may take it as an incident where the event horizon is very small or turning infinitely small with the increment of d. This is found in figs. 1(a) and (b), where we see the rate increment of interior volume with advanced time reduces down abruptly if the dimension is increased.
Fig. 1: The variations of 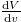 with respect to m for different dimensions d for q = 0 (a) and q > 0 (b).
with respect to m for different dimensions d for q = 0 (a) and q > 0 (b).
Download figure:
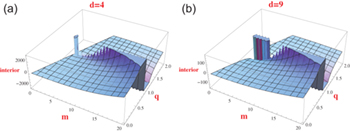
Standard imageIf the mass of the BH is increased then the rate of increment of interior volume increases. Increment in mass primarily increases the radius of event horizon and hence the interior volume. Besides these phenomena, the gravitational attraction power increases with the increment in mass. This again leads to further increment in volume, i.e., an increment in the volume increases the rate of increment of mass. But staying at a same mass if we increase the static charge, due to Pauli's exclusion principle the rate of change of volume should be deceased up to a certain level of charge, 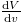 stays same and, after a certain critical value of q,
stays same and, after a certain critical value of q, 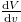 falls abruptly (figs. 2(a) and (b)).
falls abruptly (figs. 2(a) and (b)).
Fig. 2: The variations of 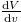 with respect to m and q for d = 4 (a) and d = 9 (b).
with respect to m and q for d = 4 (a) and d = 9 (b).
Download figure:
Standard imageEntropy in the volume of d-dimensional Reissner-Nordstrom black hole
In ref. [20], the authors have established the expression of number of quantum states with energy less than E as

the Helmholtz free energy and the pressure as

where β is the inverse of the Hawking temperature Th, i.e.,  . Here the exotic features of the interior volume is temporarily ignored.
. Here the exotic features of the interior volume is temporarily ignored.
Thus, the entropy in the interior is calculated as

This expression of the entropy in the interior is actually based on the two impotant assumptions mentioned in refs. [14,15,32] as follows: i) the Hawking radiation of a BH may be considered as black body radiation. Thus, the temperature of radiation can be supposed as the temperature on event horizon and ii) the evaporation process is considered as slow enough as that taking place in the quasi-static process. Thus, between the event horizon and the scalar field inside the BH, the thermal equilibrium can be established.
To calculate the relationship between the changes in entropy of scalar field and that of Bekenstein-Hawking entropy, we use the differential form directly. The two methods that generally are used to measure the changes in entropy of scalar field cannot be applied in our case. Those are i) method of equilibrium statics and ii) method of integral.
If we assume that only the Hawking radiation is responsible for losing the mass of the BH, then by Stefan-Boltzmann law [33,34], we have

where γ is a positive constant which depends on the number of quantized matter fields coupling with gravity, Ah denotes the area of the BH at event horizon, respectively, and they are given as

The internal energy 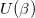 , enthalpy
, enthalpy 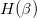 and Gibb's free energy
and Gibb's free energy 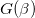 in the interior of the BH are obtained as
in the interior of the BH are obtained as

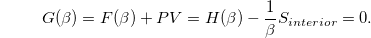
In ref. [3], the authors showed that the maximal volume sustains until the last stage of black body evaporation. The radiation may last at this point. Thus, for this BH, we obtain

Here the mass parameter m is not a constant quantity, due to Hawking radiation. It changes with advanced time v. Substituting eq. (16) in eq. (8), we obtain the differential form of interior volume as

Substituting eqs. (14) and (17) in the differential form of entropy in the interior of the BH, we obtain

The entropy of this kind of BHs on the event horizon rh is obtained directly from the definition of the Bekenstein-Hawking entropy along with and the differential form of this entropy will be

The ratio of the differential form of entropy in the interior to that on the event horizon of the BHs is given as

In figs. 3(a) and (b), we have plotted interior entropy vs. m for different dimensions. Sinterior exponentially raises due to the increment in m. If dimension is high, entropy is lower than the lower-dimensional case. Increment in dimension reduces the quantity of wrapped region of the event horizon which may lead to the decrease in entropy, i.e., the amount of disturbances enclosed by the horizon.
Fig. 3: The variation of Sinterior with respect to m for different dimensions d for q = 0 (a) and q > 0 (b).
Download figure:
Standard imageWith m and charge q, the changes of interior entropy is protrayed in figs. 4(a) and (b). We observe that q must have an upper limit for physical cases and for high charge, interior entropy increases. High change is responsible for high valued radius of event horizon. This indirectly increases interior entropy.
Fig. 4: The variations of Sinterior with respect to m and q for d = 4 (a) and  (b).
(b).
Download figure:
Standard imageBrief discussions and conclusions
It is obvious that the quantity of volume wrapped by the event horizon of a BH depends on the concerned nature of the hypersurface on which the BH is embedded. Mass of the BH, charge or dimension and many more physical properties may act as the controller. Use of Eddington-Finkelstein coordinates  and introduction of advanced time together convince us to have the expression of interior volume of a BH which is dependent on the advanced time and the corresponding ADM mass. We try to calculate the interior volume trapped inside the event horizon of a higher-dimensional BH. Previously, in other articles [35,36], it was shown that if we consider the higher dimensions it is likely to have naked singularity rather than a BH wrapped by event horizon. Not having an event horizon is equivalent to having a very small radius of event horizon (as large as possible). This shows from eq. (15) that the internal energy for a constant volume obeys the Stefan's law, i.e., the temperature to the power-four law. Again for constant temperature, the internal energy is proportional to the volume. As we increase the span of the space-time confined in a BH's event horizon, we observe that a higher amount of internal energy is trapped inside it. For enthalpy the dependence on temperature and volume is quite the same except for the fact that the enthalpy is higher than that of internal energy. This is obvious as a pressure times volume amount of energy is added to the internal energy. Gibb's free energy, however, is found to vanish. This implies that the reaction is at equilibrium and no more work is allowed. This will give us a small interior volume and hence a large/blown to infinity slope of volume for low dimensions will decrease with increasing dimension. This is what we found in the plots given in figs. 1(a) and (b). Again presence of charge should try to bind the celestial object up in the smaller boundary radius/the low radius event horizon due to "Pauli's exclusion principle". This is found in the figs. 2(a) and (b). Entropy of a BH is increasing function of the radius of event horizon. But it seems as dimension is high, entropy is low (see figs. 3(a), 4(b)). Involvement of higher dimension may be the cause for reducing the disturbances confined in the event horizon of higher dimensions. This is justified by the increment in degrees of freedom.
and introduction of advanced time together convince us to have the expression of interior volume of a BH which is dependent on the advanced time and the corresponding ADM mass. We try to calculate the interior volume trapped inside the event horizon of a higher-dimensional BH. Previously, in other articles [35,36], it was shown that if we consider the higher dimensions it is likely to have naked singularity rather than a BH wrapped by event horizon. Not having an event horizon is equivalent to having a very small radius of event horizon (as large as possible). This shows from eq. (15) that the internal energy for a constant volume obeys the Stefan's law, i.e., the temperature to the power-four law. Again for constant temperature, the internal energy is proportional to the volume. As we increase the span of the space-time confined in a BH's event horizon, we observe that a higher amount of internal energy is trapped inside it. For enthalpy the dependence on temperature and volume is quite the same except for the fact that the enthalpy is higher than that of internal energy. This is obvious as a pressure times volume amount of energy is added to the internal energy. Gibb's free energy, however, is found to vanish. This implies that the reaction is at equilibrium and no more work is allowed. This will give us a small interior volume and hence a large/blown to infinity slope of volume for low dimensions will decrease with increasing dimension. This is what we found in the plots given in figs. 1(a) and (b). Again presence of charge should try to bind the celestial object up in the smaller boundary radius/the low radius event horizon due to "Pauli's exclusion principle". This is found in the figs. 2(a) and (b). Entropy of a BH is increasing function of the radius of event horizon. But it seems as dimension is high, entropy is low (see figs. 3(a), 4(b)). Involvement of higher dimension may be the cause for reducing the disturbances confined in the event horizon of higher dimensions. This is justified by the increment in degrees of freedom.
Acknowledgments
This research is supported by the project grant of Government of West Bengal, Department of Higher Education, Science and Technology and Biotechnology (File No. ST/P/S&T/16G-19/2017). RB thanks IUCAA, PUNE for Visiting Associateship.
Appendix:
Equation (10) gives
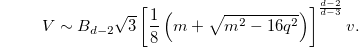
For d-dimensional spacetime, when q = 0, the equation reduces to
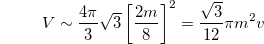
and this reduces to an asymptotically flat Schwarzschild black hole with ADM mass M as