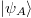Abstract
For a quantum pure state in conformal field theory, we generate the Shannon entropy of its coherence, that is, the von Neumann entropy obtained by introducing quantum measurement errors. We give a holographic interpretation of this Shannon entropy, based on Swingle's interpretation of anti-de Sitter space/conformal field theory (AdS/CFT) correspondence in the context of AdS3/CFT2. As a result of this interpretation, we conjecture a differential geometrical formula for the Shannon entropy of the coherence of a quantum pure or purified state in CFT2 at thermal and momentum equilibrium as the sum of the holographic complexity and the abbreviated action, divided by πℏ, in the bulk domain enclosed by the Ryu-Takayanagi curve. This result offers a definition of the action of a bulk model of qubits dual to the boundary CFT2 at this equilibrium.
Export citation and abstract BibTeX RIS
Introduction
In ref. [1], von Neumann proposed basic ideas for two methods of quantum measurements. The first method is to trace out the quantum state of the measurement apparatus, that is, the environment of the measured system after the measurement apparatus and the measured system interact and their states become entangled. The second method is the use of the superselection rules obtained by introducing quantum measurement errors [2–4]. These quantum measurements are changes of the given pure state of the measured system to a mixed state, that is, an exact statistical mixture of pure eigenstates of the measured quantity. So, we can identify these quantum measurements with the sources that generate the von Neumann entropy.
Recently, the translation of the von Neumann entropy, which accompanies the change of a quantum pure state to a statistical mixture, into a differential geometrical quantity in the language of gravity via anti-de Sitter space/conformal field theory (AdS/CFT) correspondence [5–8] —the example of the holographic principle [9–11]— has been extensively studied [12]. The renowned Ryu-Takayanagi formula and its covariant extension [13–16] apply von Neumann's first method of quantum measurement to the pure state of two mutually entangled quantum systems that are geometrically complementary to each other in CFT and interpret the generated von Neumann entropy, called the entanglement entropy, of the target system as a differential geometrical quantity on the gravity side.
However, no study has addressed the holographic dual of the von Neumann entropy generated by von Neumann's second method of quantum measurement that can be applied to an arbitrary quantum pure state of the target system.
In this letter, we attempt to translate into the language of gravity the Shannon entropy of the coherence of a quantum pure or purified state in CFT2 without gravity at thermal and momentum equilibrium; this Shannon entropy is obtained by the second method of quantum measurement and is the information lost by describing the quantum pure state in the classical way. This translation is done by using AdS3/CFT2 correspondence based on Swingle's interpretation [5–8,17] and provides a definition of the action of a bulk model of qubits dual to the boundary CFT2 at this equilibrium. Throughout this letter, we choose  as the signature of the AdS3 space-time metric and adopt the natural system of units, and hatted variables are quantum operators.
as the signature of the AdS3 space-time metric and adopt the natural system of units, and hatted variables are quantum operators.
Generation of the von Neumann entropy
From here, we study the holographic dual of the origin of the von Neumann entropy generated by the second method of quantum measurement of a quantum system A.
For the sake of simplicity, A consists of a particle up to (11). The argument is based on the mathematical theorem below, which was proven by von Neumann [1,2].
Theorem (von Neumann). Consider the measurement errors  and
and 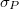 of the canonical variables
of the canonical variables 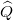 (position) and
(position) and 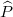 (momentum), respectively, of a spatial dimension of A. Then, under the condition
(momentum), respectively, of a spatial dimension of A. Then, under the condition

there are errors  and
and  such that the redefined
such that the redefined 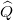 and
and  that incorporate these errors commute with each other and are able to be simultaneously measured.
that incorporate these errors commute with each other and are able to be simultaneously measured.
In this theorem, we partition the spectrum lines of 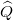 and
and 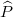 into an infinite number of intervals of constant widths
into an infinite number of intervals of constant widths 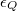 and
and 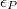 (which satisfy the equality
(which satisfy the equality  [1]), respectively, and we replace these canonical variables with
[1]), respectively, and we replace these canonical variables with  and
and 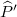 , which take constant eigenvalues in each of their intervals. Specifically, the spectra of
, which take constant eigenvalues in each of their intervals. Specifically, the spectra of  and
and  are
are

and

respectively. In this theorem, because  and
and  commute, we can consider the phase space of A as in classical mechanics. This phase space is divided into the Planck cells specified by (2) and (3), and there is one possible redefined quantum orbital state for each Planck cell.
commute, we can consider the phase space of A as in classical mechanics. This phase space is divided into the Planck cells specified by (2) and (3), and there is one possible redefined quantum orbital state for each Planck cell.
When all (orbital) observables  of A are able to be simultaneously measured within certain measurement errors
of A are able to be simultaneously measured within certain measurement errors 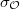 (i.e., when only such approximate measurements are made for A), we say that A is in a macroscopic state (distinct from the term macrostate in statistical mechanics) [2–4]. A macroscopic state of A is determined by the corresponding set of observables
(i.e., when only such approximate measurements are made for A), we say that A is in a macroscopic state (distinct from the term macrostate in statistical mechanics) [2–4]. A macroscopic state of A is determined by the corresponding set of observables 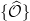 of A that is restricted from the total set of Hermitian operators. This set of observables is a set of commutative elements because they can be simultaneously measured (i.e., are classicalized) [3,4]1
. Here, note that all orbital observables, that is, all polynomials of the redefined position and momentum operators of the particle, are classicalized in the sense of classicalization à la von Neumann.
of A that is restricted from the total set of Hermitian operators. This set of observables is a set of commutative elements because they can be simultaneously measured (i.e., are classicalized) [3,4]1
. Here, note that all orbital observables, that is, all polynomials of the redefined position and momentum operators of the particle, are classicalized in the sense of classicalization à la von Neumann.
Now, in a macroscopic state of A, for any polynomial operator  of
of  and
and  , the superselection rules
, the superselection rules

hold. We denote by 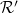 a pair comprising the redefined position
a pair comprising the redefined position  in the spectrum (2) and the redefined momentum
in the spectrum (2) and the redefined momentum 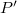 in the spectrum (3). When
in the spectrum (3). When 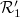 and
and  are distinct,
are distinct,  and
and 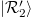 have no coherence [2–4]. The reason for this is that
have no coherence [2–4]. The reason for this is that

holds for 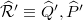 . From this fact, when A is in a macroscopic state, the superposition of simultaneous eigenstates
. From this fact, when A is in a macroscopic state, the superposition of simultaneous eigenstates  of
of  and
and 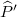 , made distinct by spectrum width, becomes a statistical mixture: the von Neumann entropy is generated. Indeed, by expanding the given quantum pure state
, made distinct by spectrum width, becomes a statistical mixture: the von Neumann entropy is generated. Indeed, by expanding the given quantum pure state 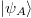 to
to

it follows that

where  are Gaussian wave packets of the original position Q with width
are Gaussian wave packets of the original position Q with width 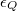 and Fourier width
and Fourier width 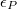 , and their full set forms a complete orthonormal system of the functional Hilbert space of A [1]. Namely, by introducing measurement errors of A that satisfy (1), the von Neumann entropy
, and their full set forms a complete orthonormal system of the functional Hilbert space of A [1]. Namely, by introducing measurement errors of A that satisfy (1), the von Neumann entropy


is generated from the superposition of the simultaneous eigenstates 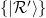 of
of 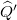 and
and 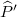 (an arbitrary quantum pure state) of A. By using the Shannon entropy in bits
(an arbitrary quantum pure state) of A. By using the Shannon entropy in bits

we can write the von Neumann entropy as

Equation (10) is the information lost by introducing measurement errors (i.e., by the classicalization of the given quantum pure state  ).
).
Finally, we consider the case of a system in quantum field theory (QFT). For a system in QFT, we adopt the interaction picture in order to define a particle (i.e., its position and momentum eigenstates) of a field. In the classicalization of a system in QFT2, due to the measurement errors, to describe the positions and momenta of particles with sufficient fineness, we must introduce the ultraviolet cutoff, that is, the lattice constant  , for the boundary line and its reciprocal constant (refer to the fifth paragraph of the next section). Then, noting that all redefined orbital number operators are classicalized (i.e., have simultaneous eigenstates), the Shannon entropy of the coherence of a system in QFT2 on this lattice and its reciprocal (i.e., a quantum many-body system) is defined as in quantum mechanics as explained so far.
, for the boundary line and its reciprocal constant (refer to the fifth paragraph of the next section). Then, noting that all redefined orbital number operators are classicalized (i.e., have simultaneous eigenstates), the Shannon entropy of the coherence of a system in QFT2 on this lattice and its reciprocal (i.e., a quantum many-body system) is defined as in quantum mechanics as explained so far.
AdS/CFT correspondence
Next, we apply the AdS3/CFT2 correspondence based on Swingle's interpretation to a quantum pure state 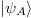 of a quantum system A in a strongly coupled CFT in two-dimensional Minkowski space-time [5–8,17]. In this application, we consider the change of bulk induced by the measurement errors. In this section, we consider static and classical bulk space-time at zero boundary temperature, which corresponds to the ground state of an isolated quantum system A.
of a quantum system A in a strongly coupled CFT in two-dimensional Minkowski space-time [5–8,17]. In this application, we consider the change of bulk induced by the measurement errors. In this section, we consider static and classical bulk space-time at zero boundary temperature, which corresponds to the ground state of an isolated quantum system A.
In the bulk space, we consider the bubble, defined for the domain A sitting on the boundary,

The symbol ∼ indicates homology equivalence.
In Swingle's interpretation based on Vidal's multiscale entanglement renormalization ansatz (MERA), a quantum pure state on a lattice in the boundary space is equivalent to the tensor network of qubits (here, we assume that the fermionic occupancy/empty states at each site on the lattice in the second quantization characterize the qubit states) obtained by the entanglement renormalization group transformation in the bulk space and each bubble  of A transverses this tensor network [17–19]. Here, the entanglement renormalization group transformation is the real-space renormalization group transformation of the semi-infinitely alternate combinations of the disentangler that makes the entanglement between two adjacent qubits be the product state by a unitary transformation and an isometry that adjoins two adjacent qubits into one qubit by coarsening the grain [18]. The sequence of this transformation of qubits is a scale-invariant tensor network [18,19].
of A transverses this tensor network [17–19]. Here, the entanglement renormalization group transformation is the real-space renormalization group transformation of the semi-infinitely alternate combinations of the disentangler that makes the entanglement between two adjacent qubits be the product state by a unitary transformation and an isometry that adjoins two adjacent qubits into one qubit by coarsening the grain [18]. The sequence of this transformation of qubits is a scale-invariant tensor network [18,19].
Now, we denote by GN the three-dimensional Newton's gravitational constant. Then, as the Ryu-Takayanagi formula of the entanglement entropy [13,14]

holds in a static AdS3 space-time, it is known that, for a sufficiently strongly entangled system A,

holds in Swingle's interpretation [12]. Here, denoting by  the geodesic bubble,
the geodesic bubble,  gives rise to the values of (13) and (14). Before we introduce the measurement errors, the holographic dual,
gives rise to the values of (13) and (14). Before we introduce the measurement errors, the holographic dual,  , of the quantum pure state of A in a static AdS3 space-time is, by formula (14), the bulk domain whose boundary is specified by the geodesic bubble
, of the quantum pure state of A in a static AdS3 space-time is, by formula (14), the bulk domain whose boundary is specified by the geodesic bubble 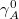 and A (the so-called time slice of the entanglement wedge of A in the bulk):
and A (the so-called time slice of the entanglement wedge of A in the bulk):

Next, we introduce the quantum measurement errors 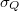 and
and 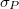 fine enough to describe positions and momenta of the system A such that the spectrum lattices of (2) and (3), respectively, match the lattice and its reciprocal. Then, over the whole of the boundary, no redefined position eigenstate has coherence with any other due to (5). So, as in (7), the state of an arbitrary system of different sites on the boundary is a statistical mixture of product eigenstates of redefined positions and has no entanglement. From this fact, in the bulk space, there are no disentangler operations in the entanglement renormalization group transformation, by which the tensor network (that is, the holographic dual of the quantum systems on the boundary) works. Namely, both on the whole of the boundary and also in the whole of the tensor network in the bulk space, there is no coherence and there are no EPR pairs. Consequently, for the pure states in the mixed state of A, all the bubbles
fine enough to describe positions and momenta of the system A such that the spectrum lattices of (2) and (3), respectively, match the lattice and its reciprocal. Then, over the whole of the boundary, no redefined position eigenstate has coherence with any other due to (5). So, as in (7), the state of an arbitrary system of different sites on the boundary is a statistical mixture of product eigenstates of redefined positions and has no entanglement. From this fact, in the bulk space, there are no disentangler operations in the entanglement renormalization group transformation, by which the tensor network (that is, the holographic dual of the quantum systems on the boundary) works. Namely, both on the whole of the boundary and also in the whole of the tensor network in the bulk space, there is no coherence and there are no EPR pairs. Consequently, for the pure states in the mixed state of A, all the bubbles  containing
containing  and all the bulk domains
and all the bulk domains 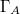 (s.t.
(s.t.  ) containing
) containing  , the time slice of the entanglement wedge of A in the bulk, cannot be distinguished from each other. In other words, information of
, the time slice of the entanglement wedge of A in the bulk, cannot be distinguished from each other. In other words, information of 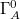 as the time slice of the entanglement wedge of A in the bulk is lost.
as the time slice of the entanglement wedge of A in the bulk is lost.
From this consequence, the holographic dual 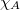 of A in the bulk space has a microstate (in the sense of statistical mechanics) for each bulk domain
of A in the bulk space has a microstate (in the sense of statistical mechanics) for each bulk domain 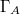 and has entropy
and has entropy 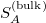 with value (9) from the holographic principle.
with value (9) from the holographic principle.
As statistical mechanics reveals, the origin of the bulk entropy  generated by the measurement errors is the number of microstates of
generated by the measurement errors is the number of microstates of 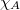 . (Before we introduce measurement errors, (8) is zero and the microstate of
. (Before we introduce measurement errors, (8) is zero and the microstate of  is uniquely specified by
is uniquely specified by 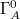 .) This origin is clearly different from the origin of the bulk entropy generated by the partial trace over the geometrically complementary system on the boundary (i.e., by the first method of quantum measurement).
.) This origin is clearly different from the origin of the bulk entropy generated by the partial trace over the geometrically complementary system on the boundary (i.e., by the first method of quantum measurement).
Holographic interpretation
In the second method of quantum measurement, the holographic interpretation follows from the above arguments.
For a given quantum pure state  of the boundary system A in contact with an energy and momentum reservoir [20,21]2
, we consider the Shannon entropy
of the boundary system A in contact with an energy and momentum reservoir [20,21]2
, we consider the Shannon entropy 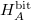 of its coherence in bits. This entropy is the information lost by the introduction of measurement errors. We assume that the measurement errors
of its coherence in bits. This entropy is the information lost by the introduction of measurement errors. We assume that the measurement errors  and
and  are fine enough to describe A, as mentioned in the last section. In our setup, we propose that
are fine enough to describe A, as mentioned in the last section. In our setup, we propose that

where CA is the holographic complexity of A and is given essentially by the area of the holographic dual 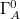 of A for the geodesic bubble
of A for the geodesic bubble  [22–25]3
, and IA is the value of the action
[22–25]3
, and IA is the value of the action ![$I[\Gamma_A]$](https://content.cld.iop.org/journals/0295-5075/129/1/11006/revision1/epl20002ieqn75.gif) taken at
taken at 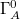 .
.
Here, the action ![$I[\Gamma_A]$](https://content.cld.iop.org/journals/0295-5075/129/1/11006/revision1/epl20002ieqn77.gif) is defined in the following way. First, we decompose the square of line elements of the bulk space-time by using the metric
is defined in the following way. First, we decompose the square of line elements of the bulk space-time by using the metric  of the two-dimensional space-times and an Arnowitt-Deser-Misner–like method as
of the two-dimensional space-times and an Arnowitt-Deser-Misner–like method as

where r is the extra dimension [26]. In this decomposition, the action ![$I[\Gamma_A]$](https://content.cld.iop.org/journals/0295-5075/129/1/11006/revision1/epl20002ieqn79.gif) is defined, in the family of phase spaces of the two-dimensional space-like hypersurface
is defined, in the family of phase spaces of the two-dimensional space-like hypersurface 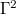

for momentum density px of the slice of  at each position r of the extra dimension [26], as
at each position r of the extra dimension [26], as

where the index x is contracted by the Kronecker delta (see the arguments after (33)). This action is the abbreviated action in the family of phase spaces  .
.
Proposal (16) is based on the following arguments. First, we expand the given quantum pure state 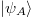 of the system A to
of the system A to  and set
and set ![$p_A[\{{{\psi}^{\rm basis}}\}_n]=|c_n|^2$](https://content.cld.iop.org/journals/0295-5075/129/1/11006/revision1/epl20002ieqn85.gif) . Here,
. Here, 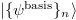 are equivalent to distinct product simultaneous eigenstates
are equivalent to distinct product simultaneous eigenstates 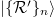 of the redefined positions
of the redefined positions  and redefined momenta
and redefined momenta 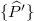 with many-body degrees of freedom; we omit the tilde part [21]. Next, we consider the bulk side. After introducing quantum measurement errors,
with many-body degrees of freedom; we omit the tilde part [21]. Next, we consider the bulk side. After introducing quantum measurement errors, 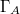 (that is, a microstate of
(that is, a microstate of  ) has a normalized distribution function,
) has a normalized distribution function, ![$f[\Gamma_A]$](https://content.cld.iop.org/journals/0295-5075/129/1/11006/revision1/epl20002ieqn92.gif) . As the consequence of the last section's main argument, instances of
. As the consequence of the last section's main argument, instances of  cannot be distinguished from each other and are uniformly distributed over their configuration space. So, due to Tolman's principle of equal a priori probabilities [27],
cannot be distinguished from each other and are uniformly distributed over their configuration space. So, due to Tolman's principle of equal a priori probabilities [27],

holds for the number of states  . Here, the equal a priori probability
. Here, the equal a priori probability 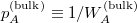 is determined by the horizontal bulk-space momentum density px, which is an additive quantity, its multiplier for the momentum constraint, and the geometry of
is determined by the horizontal bulk-space momentum density px, which is an additive quantity, its multiplier for the momentum constraint, and the geometry of 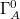 via maximization of the number of microstates subject to the a posteriori number and momentum constraints in the bulk space. In the gravitational theory dual to the CFT of the boundary, the multiplier of px is the "shift vector" vx. This multiplier vx is obtained from the thermodynamic relation4
via maximization of the number of microstates subject to the a posteriori number and momentum constraints in the bulk space. In the gravitational theory dual to the CFT of the boundary, the multiplier of px is the "shift vector" vx. This multiplier vx is obtained from the thermodynamic relation4

for the horizontal bulk-space entropy density 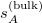 (s.t.
(s.t.  for the area form of the bulk-space entropy density
for the area form of the bulk-space entropy density 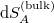 ) and the inverse bulk-space temperature
) and the inverse bulk-space temperature  under the identification
under the identification

for the curvature radius  of AdS3 space-time, a dimensionless "time" parameter
of AdS3 space-time, a dimensionless "time" parameter  defined by the relation
defined by the relation 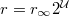 for the ultraviolet cut-off
for the ultraviolet cut-off  of the extra dimension r, and a dimensionless positive real constant κ: this is when we regard the entanglement renormalization group transformation as being like inverse time evolution [12]. (Here, the range of
of the extra dimension r, and a dimensionless positive real constant κ: this is when we regard the entanglement renormalization group transformation as being like inverse time evolution [12]. (Here, the range of 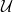 is
is  at zero boundary temperature [17]; at finite boundary temperatures, we paste two truncated MERA networks together at the position of the black hole event horizon [21].) Then, the equal a priori probability
at zero boundary temperature [17]; at finite boundary temperatures, we paste two truncated MERA networks together at the position of the black hole event horizon [21].) Then, the equal a priori probability 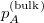 is the value of the next factor taken at the holographic dual
is the value of the next factor taken at the holographic dual  of the quantum pure state of A:
of the quantum pure state of A:

This probability gives rise to the entropy  of
of  (i.e., the information lost about
(i.e., the information lost about  )5
.
)5
.
From the above arguments and the holographic principle, the Shannon entropy  of the quantum mixed state of A in nats is
of the quantum mixed state of A in nats is







The conjectured part (26), that is, an equality between entropy (i.e., lost information) in the boundary and the bulk is based on the holographic principle. Here, the integral measure 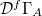 satisfies
satisfies

Hydrodynamics
Next, to estimate the abbreviated action IA, let us consider the hydrodynamics of the CFT2 of the boundary (i.e., the system A plus the reservoir), which is perfectly described by conserved quantities and does not require the local equilibrium condition because it is two-dimensional [28–30]. Specifically, we consider the gravity dual of a one-dimensional perfect fluid with uniform and steady fluid two-velocity 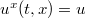 and
and 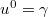 such that
such that

for the Lorentz metric 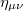 of the two-dimensional boundary space-time, energy density ε, pressure
of the two-dimensional boundary space-time, energy density ε, pressure  , and "mass" density
, and "mass" density  ; we denote the kinetic part of ε by
; we denote the kinetic part of ε by  . Then, the metric of the bulk space-time, that is, the Schwarzschild AdS3 black hole (i.e., the nonrotating Bañados-Teitelboim-Zanelli black hole [31]), Lorentz boosted in the bulk space-time with the two-velocity
. Then, the metric of the bulk space-time, that is, the Schwarzschild AdS3 black hole (i.e., the nonrotating Bañados-Teitelboim-Zanelli black hole [31]), Lorentz boosted in the bulk space-time with the two-velocity  , is
, is

In this metric,  is covariantized with respect to Lorentz transformations in the boundary directions, where the index of
is covariantized with respect to Lorentz transformations in the boundary directions, where the index of 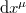 is lowered by
is lowered by 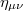 due to (32). Here, we scale the curvature radius of AdS3 space-time to unity (i.e.,
due to (32). Here, we scale the curvature radius of AdS3 space-time to unity (i.e., 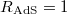 ) and denote the radius of the event horizon of the Schwarzschild AdS3 black hole taken to be equal to unity by
) and denote the radius of the event horizon of the Schwarzschild AdS3 black hole taken to be equal to unity by  [23,24]. We denote the discrepancy between the metrics
[23,24]. We denote the discrepancy between the metrics 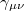 and
and 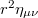 by
by 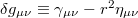 . Then, from the one-dimensional Stefan-Boltzmann law of fluid of massless particles, we obtain
. Then, from the one-dimensional Stefan-Boltzmann law of fluid of massless particles, we obtain  for the horizontal bulk-space momentum density px [26]. In addition to this, we have
for the horizontal bulk-space momentum density px [26]. In addition to this, we have  .
.
We let the domain of the system in the boundary be ![$A:[0,l]$](https://content.cld.iop.org/journals/0295-5075/129/1/11006/revision1/epl20002ieqn132.gif) . Because (33) is three-dimensional, (33) is locally the metric of AdS3 [32] and so is compatible with Swingle's interpretation of AdS/CFT correspondence; this fact is why we set this study in the context of AdS3/CFT2. In the Poincarè coordinates, the geodesic
. Because (33) is three-dimensional, (33) is locally the metric of AdS3 [32] and so is compatible with Swingle's interpretation of AdS/CFT correspondence; this fact is why we set this study in the context of AdS3/CFT2. In the Poincarè coordinates, the geodesic 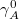 in the bulk is a half-circle. The area element in the bulk space is given in the Poincar
in the bulk is a half-circle. The area element in the bulk space is given in the Poincar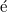 metric of AdS3 by
metric of AdS3 by

where z = 0 represents the boundary. Using these, in the "non-relativistic" regime (i.e.,  ), when the lattice constant
), when the lattice constant  is sufficiently small relative to l and
is sufficiently small relative to l and  , we obtain the abbreviated action
, we obtain the abbreviated action



Here,

is the minimum elapsed time (the Margolus-Levitin time) required to execute a binary classical logic gate as a change of an original quantum pure state to another quantum pure state orthogonal to the original state (that is, a classical mechanically different state) [33–35], and  is the central charge of the CFT2 of the boundary [36].
is the central charge of the CFT2 of the boundary [36].
With this hydrodynamics, the proposal (16) is reduced to two conceptual arguments in terms of complexity: i) after introducing quantum measurement errors, the quantum mixed state of the boundary system A, obtained by (7), has classical probabilities (i.e., probabilities with no interference). In addition to this, 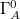 is the holographic dual of this quantum mixed state of A because the relative phases in
is the holographic dual of this quantum mixed state of A because the relative phases in 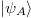 are redundant for the geometry of
are redundant for the geometry of 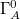 . Then,
. Then,  is the spatial realization of the minimum program (i.e., the program with no redundancy), whose union of N replicas outputs the statistical mixture (7) of N product simultaneous eigenstates
is the spatial realization of the minimum program (i.e., the program with no redundancy), whose union of N replicas outputs the statistical mixture (7) of N product simultaneous eigenstates  of redefined positions
of redefined positions 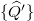 and redefined momenta
and redefined momenta  of A, that is, the quantum mixed state of A in the limit as N goes to infinity. This output is done independently by means of
of A, that is, the quantum mixed state of A in the limit as N goes to infinity. This output is done independently by means of 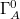 itself and a binary classical computer with the Margolus-Levitin time
itself and a binary classical computer with the Margolus-Levitin time  . The spatial length of this program is
. The spatial length of this program is

ii) The dimensionless length of this minimum program is

and is the Shannon entropy (10) of the quantum mixed state (7) of A. If 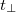 were not the shortest Margolus-Levitin time, then
were not the shortest Margolus-Levitin time, then 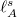 would not be minimal because the true length of the minimum program is unique. In these arguments, whereas
would not be minimal because the true length of the minimum program is unique. In these arguments, whereas  is independent of the state of fluid,
is independent of the state of fluid, 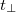 is determined by the state of fluid. Argument ii) is based on the fact that the Shannon entropy of a quantum mixed state can be written as the ensemble average of the classical Kolmogorov complexity [37]6
.
is determined by the state of fluid. Argument ii) is based on the fact that the Shannon entropy of a quantum mixed state can be written as the ensemble average of the classical Kolmogorov complexity [37]6
.
Consideration of the proposal in two models
Up to now, we have studied the holographic Shannon entropy of the CFT2 coherence in the bulk. There, we relied on classical statistical mechanics and invoked the ideas of complexity. In this section, considering two one-dimensional models, we check our proposal (16) for the boundary qubits state by using a discrete holographic tensor network. Here, the Shannon entropy of the coherence of the target system A can be written in the Boltzmann form  in terms of the number of classicalized (boundary) microstates
in terms of the number of classicalized (boundary) microstates 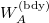 due to the measurement errors and the number
due to the measurement errors and the number  of elements in the statistical ensemble of A.
of elements in the statistical ensemble of A.
First, we consider the ground state of the target system A in a strongly coupled CFT2, where the classicalized microstates are counted by their real-space degrees of freedom (dual to the MERA network of A) only, due to  . We recall that, because of the Stirling formula, the disentangler operations and the isometries of EPR pairs in each layer of the MERA reduce the number of classicalized microstates to
. We recall that, because of the Stirling formula, the disentangler operations and the isometries of EPR pairs in each layer of the MERA reduce the number of classicalized microstates to  of the unreduced number per site in the deeper layer of the MERA. In this way, we obtain
of the unreduced number per site in the deeper layer of the MERA. In this way, we obtain  for the number of classicalized microstates
for the number of classicalized microstates  and the number of sites lm in the m-th layer
and the number of sites lm in the m-th layer  of the MERA of A. Here, the 0th layer is the boundary. At the deepest M-th layer, we have
of the MERA of A. Here, the 0th layer is the boundary. At the deepest M-th layer, we have  . Consequently, we find that
. Consequently, we find that


which is the discretized area of  . The generalization of this result to a finite temperature system is straightforward by applying the result of ref. [21].
. The generalization of this result to a finite temperature system is straightforward by applying the result of ref. [21].
Second, we consider the thermal and momentum equilibrium state of the target system A in a CFT2 perfect fluid in the "non-relativistic" regime. This momentum equilibrium state of A is obtained from the thermal equilibrium state of A, dual to two MERA networks of A [21], by transforming the coordinate system (t, x) of the boundary alongside the moving reservoir and transforming the Hamiltonian  of A, using
of A, using



for the total momentum  of A and the kinetic energy
of A and the kinetic energy  of A with the velocity
of A with the velocity  of the reservoir [20]. Here, we regard the average of the second term in (45) with respect to A as the Hamiltonian of the a posteriori momentum constraint C of A with the multiplier
of the reservoir [20]. Here, we regard the average of the second term in (45) with respect to A as the Hamiltonian of the a posteriori momentum constraint C of A with the multiplier 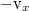 of C and decompose this constraint C into its minimal (mutually exclusive) momentum subconstraints. Then, because the phase-space description of A is well-defined by the classicalization due to the measurement errors, when we count the number of classicalized microstates of A, there are as many replicas of the MERA of A (in addition to the original MERA of A) in the real space as these minimal momentum subconstraints of C. At the decomposition of the constraint C, note that the energy
of C and decompose this constraint C into its minimal (mutually exclusive) momentum subconstraints. Then, because the phase-space description of A is well-defined by the classicalization due to the measurement errors, when we count the number of classicalized microstates of A, there are as many replicas of the MERA of A (in addition to the original MERA of A) in the real space as these minimal momentum subconstraints of C. At the decomposition of the constraint C, note that the energy  has the thermal time (i.e., the decoherence time)
has the thermal time (i.e., the decoherence time) 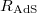 [23,24] as its Margolus-Levitin time. Namely,
[23,24] as its Margolus-Levitin time. Namely,  is the minimum accessible energy width defined for a subconstraint of C. Then, the number of minimal momentum subconstraints of C (i.e., the number of replicas of the MERA of A in the real space) is the division of the energy of C by this energy width
is the minimum accessible energy width defined for a subconstraint of C. Then, the number of minimal momentum subconstraints of C (i.e., the number of replicas of the MERA of A in the real space) is the division of the energy of C by this energy width 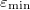 , that is,
, that is,  for the Margolus-Levitin time
for the Margolus-Levitin time 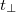 given by (38). Now, the number of classicalized microstates
given by (38). Now, the number of classicalized microstates  is the product of the numbers of classicalized microstates
is the product of the numbers of classicalized microstates  of the i-th MERA of A
of the i-th MERA of A  . That is, we have
. That is, we have

The number of classicalized microstates of the MERA of A is

Consequently, we find that

Namely, in this case, the Shannon entropy is the sum of the discretized area of the bulk domain 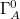 and an abbreviated action term. This is the content of our proposal (16).
and an abbreviated action term. This is the content of our proposal (16).
Conclusion: the holographic tensor network action
Finally, we derive the fundamental consequence of our proposal (16) for the AdS3/CFT2 correspondence by using two relations.
The first relation is the equality between the Shannon entropy in nats 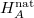 of the coherence of the thermofield-double pure state of the target system A at thermal equilibrium and the quantum thermodynamic entropy
of the coherence of the thermofield-double pure state of the target system A at thermal equilibrium and the quantum thermodynamic entropy  of A defined as the von Neumann entropy of the canonical distribution of A after the redefinition of the phase-space variables. That is, we have
of A defined as the von Neumann entropy of the canonical distribution of A after the redefinition of the phase-space variables. That is, we have


for the inverse temperature β, the energy  , and the Helmholtz free energy
, and the Helmholtz free energy

of A at the thermal equilibrium. In (51), the operator  for the redefined Hamiltonian
for the redefined Hamiltonian 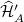 of A can be written as
of A can be written as

where



In (53) and (54), we assume the conditions  and
and  , respectively. Then, we have the relations
, respectively. Then, we have the relations  and
and  . This equality (49) is valid under replacement of thermal equilibrium by thermal and momentum equilibrium.
. This equality (49) is valid under replacement of thermal equilibrium by thermal and momentum equilibrium.
The second relation is the mainstay relation of the AdS3/CFT2 correspondence in the equilibrium case [6–8],

for the equilibrium Helmholtz free energy  of CFT2 in the large-N limit [38] and the classical gravity action
of CFT2 in the large-N limit [38] and the classical gravity action 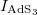 evaluated on AdS3.
evaluated on AdS3.
Combining (16), (49), and (56), we conjecture that gravity in AdS3 can be replaced by the system with the action

as the bulk theory equivalent to the boundary CFT2 at thermal and momentum equilibrium. Here, 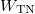 denotes our abbreviated action IA, where A refers to the holographic tensor network;
denotes our abbreviated action IA, where A refers to the holographic tensor network;  denotes the discretized area of the holographic tensor network; and b is the information of a classical bit and indicates that the holographic tensor network consists of qubits.
denotes the discretized area of the holographic tensor network; and b is the information of a classical bit and indicates that the holographic tensor network consists of qubits.
We can observe two important points from (57).
First, the first term of (57) is the abbreviated action defined for the "temporal" extra dimension r. From the abbreviated principle of stationary action subject to the CFT2 boundary condition and energy conservation, this result suggests that, in the realized holographic tensor network, the horizontal information propagation is optimal with respect to the "time". This is in agreement with (17).
Second, the second term of (57) takes the form of the action of a membrane with the tension

which is proportional to the Planck constant. This result suggests that the bulk space is quantized by the energy  per unit bulk space area.
per unit bulk space area.
We conclude this letter with the proposal (16) and this change of the perspective (57) of the AdS3/CFT2 correspondence.
Footnotes
- 1
When we introduce measurement errors, we assume that the system is in a macroscopic state.
- 2
After introducing quantum measurement errors, the equilibrium state of CFT2 can be purified by means of the tilde states
 [21].
[21]. - 3
So neither CA nor (7) contains information about the relative phases in
 .
. - 4
Note that
 , from the arguments that follow.
, from the arguments that follow. - 5
See the Supplementary Material Supplementarymaterial.pdf (SM) for the derivation of (23).
- 6
See (S19) in the SM.