Abstract
We review a strategy to use an ion-based analog quantum simulator to study the many-body electron-electron Coulomb interaction of an electron gas. This is made possible by an exact unitary dilatation mapping, which allows an experimentally challenging system to be replaced by an alternative one that may be experimentally more accessible. We show the feasibility of this simulation strategy mathematically. As a bonus, the dilatation transformation does not even need to be physically implemented when only the system spectrum is needed, in which case the simulation induces no experimental complexity overhead. This proposal is dimension-agnostic, and could be generalized as a simulation strategy between systems involving terms with different position or momentum dependence.
Export citation and abstract BibTeX RIS
Introduction
In the quantum mechanical regime, the interaction among particles can bring a variety of interesting phenomena [1]. Such many-body interactions play an integral part in our understanding of the natural world and have attracted countless research efforts over the years. However, due to the exponential growth of the Hilbert space as the number of particles increases [2], quantum many-body problems are notoriously difficult to solve, either to get a full energy spectrum or to obtain its dynamical behaviour. To date, very few realistic exactly solvable models exist, and they often rely on the use of various numerical approximation methods [3,4]. Numerically, on a classical computer the resources and time required to solve a problem exhibit a corresponding exponential growth as the Hilbert space describing such many-body systems. While some powerful numerical tools such as quantum Monte Carlo [4] methods and the density matrix renormalization group [3] may be successfully employed for some systems, one issue that typically arises is that the approximations assumed are valid only in some regions of the parameter space. For example, with the density matrix renormalization group algorithms, the resource can grow exponentially for high-dimension systems [5] and may thus fail for even relatively small systems. Therefore, the complexity involved with such systems not only makes analytical solutions extremely hard to obtain but also prevents an efficient numerical study of many other interesting problems, especially for quantum dynamics and higher-dimension systems.
Rather than performing the actual calculation, we may use an alternative method to solve this challenging problem by means of a quantum simulation [2,6–10]. Considering the simulated system, one has some initial state, which evolves under a propagator U determined by the Hamiltonian of the system to reach a final state at time t. The quantum simulation of this process is to find and implement another quantum system such that there exists a mapping between the initial (and final) states of the system and the simulator, therefore any physical measurement of the original system can be derived from the measurements on the simulator, which one may design to be experimentally more accessible, more controllable, and easier to carry out a precise measurement. There are two ways to design a quantum simulator: one may either design a digital simulator, where the propagator is realized with qubit gates, or one may design an analog simulator, where the propagator is driven by the Hamiltonian of another quantum system, which is the focus of this paper. The idea to simulate one quantum system with another has been proven [10] to be efficient, at least for any many-body system having only few-body particle correlations. Quantum simulators follow the laws of quantum mechanics, with an exponentially growing computing capability [2,6] that can match the exponential growth of problem size with particle number. Unlike a truly universal quantum computer which has yet to be realized, quantum simulators designed for specific systems have enjoyed considerable success, aided by experimental advances such as the realization of high-fidelity quantum gates and increasingly precise measurement [11,12]. Quantum simulators have been used to study quantum phase transitions [13], open quantum systems [14], and pairing Hamiltonians [15], to name just a few. Given the requirement of controllability and measurement precision, several systems have been proposed and realized experimentally to implement the quantum simulation task, including ion traps [6,9,16], ultracold atoms in optical lattices [17], NMR nuclear spins [18], and superconducting qubits [19].
Many-body electron-electron (e-e) Coulomb interactions play a critical role in many important phenomena such as the fractional quantum Hall effect [20,21] and high Tc superconductors [22]. Dealing with the mutual Coulomb interactions between all the electrons is daunting but essential to a deep understanding of such systems. In this paper, we review [23] a quantum simulation strategy using ion-based systems. The quantum simulation is based on an exact mathematical mapping between the electronic system and an ion-based system. While at first sight, the electrons and ions have a formally similar Hamiltonian containing the standard kinetic term and repulsive Coulomb interaction term, due to the non-commutative nature of the position and momentum operator a direct simulation of the electronic system with the ionic one is not possible since the electrons in the physical system to be emulated and ions in the simulator carry different masses and charges. To get around this obstacle, we have employed a dilatation transform to establish an explicit mapping between the simulator on one timescale and the interacting electrons on a different timescale. Therefore, the simulator at a rescaled time can be used to simulate the e-e Coulomb interactions. This simulation design takes into account the finite-size boundary effects for the interacting electrons, where one has bound states. One remarkable feature of our proposal is that the mapping is a unitary one, thus if only energy spectrum is desired in the readout process, the transform will not alter the spectrum so it is not necessary to generate it physically. In this case, one may choose a physical quantity to measure based on the exact experimental apparatus used and carry out a Fourier transform to derive the energy spectrum of the electronic system. This proposal is also dimension-agnostic. For example, it could simulate 2D electron gases, which can exhibit quantum Hall effects [20,21]. Or, by loading the ions in honeycomb lattices, one could also realize different topological phases for electrons in graphene-like structures [24]. To experimentally implement this quantum simulator, one possible realization may be an ion trap [6,9,16], whose control may be implemented with current technologies [11,12].
Background information
The main challenge in the calculation of the many-body electron systems is the exponential growth of the Hilbert space as the number of electrons grows. In addition, the dynamical degrees of freedom are represented by continuous variables, for which a finite-element approach is needed for each electron in a numerical calculation. Therefore, this still presents a huge obstacle in terms of the computation power needed. One notable numerical approach in dealing with an electron gas is the Monte Carlo method [4,25,26], with the caveat for the need of a good trial function for accurate results, which can be highly non-trivial. The idea behind quantum simulation is that rather than treating this exponential growth as detrimental, we use it as a resource, where the properties of a well-controlled simulator can enable one to study the properties of a hard to control system.
Generally speaking, quantum simulations [27–29] can either be done in an analog fashion, by designing a system Hamiltonian to drive the dynamics, or they can be carried out digitally, where one uses quantum gates to simulate the state evolution of the actual system. In analog simulations, one needs to find the mapping M between the system and the simulator such that the unitary propagator Us can be mapped back to the dynamics of the original system U0, driven by the Hamiltonian for the simulator and simulated system (denoted Hs and H0) respectively. On the other hand, a digital simulation strategy normally seeks to decompose the propagator akin to the Trotter formula,  , where each Hj represents local interactions involving, e.g., one- or two-qubit interactions. It is, in principle, possible to simulate any finite-dimensional local Hamiltonians with this approach [28], which may even pave the way for a universal quantum computer.
, where each Hj represents local interactions involving, e.g., one- or two-qubit interactions. It is, in principle, possible to simulate any finite-dimensional local Hamiltonians with this approach [28], which may even pave the way for a universal quantum computer.
For the quantum simulation of the electron system, trapped ions are an ideal fit since they can be well-controlled experimentally, and the Hamiltonian and Hilbert space is a good fit for the purpose. One of the most widely used ion traps is the Penning trap [30–32] which employs both electric and magnetic fields. The Penning trap can achieve a high level of control, where a single particle can be trapped [32]. The motion of the trapped particle in a Penning trap is linear [30,32], which can then be quantized, where the axial component is governed by a harmonic-oscillator–type Hamiltonian, whereas the radial cyclotron part can be close to the quantum ground state in large fields. Another type of widely used ion trap is by Wolfgang Paul [33], which uses an electromagnetic field that is both time and spatially varying. The Paul trap can be used for both neutral and charged particles and is very versatile. Trapped ions have also been used to study hybrid systems of laser-cooled trapped ions and ultracold atoms [34]. The principle for the ion trap is that the binding force needs to increase linearly with distance, 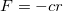 , which translates to a parabolic potential V of the general form [33]
, which translates to a parabolic potential V of the general form [33]

which also needs to fulfill the Laplace equation  at all times.
at all times.
After the state evolution, one then needs to read out the simulation results, so that the properties of the original system can be obtained. There are various approaches to achieve this. For example, one may use a quantum state tomography [35] to obtain the quantum state's wave function at the end of the simulation run. One may also do measurement for some observable O, and back-calculate the corresponding expectation value  for the actual system following the mapping between the simulator and the system.
for the actual system following the mapping between the simulator and the system.
For the specific case of ion traps, there are additional tricks one may use. It has been reported [36] that one can map the dynamics of the trapped ion's motion onto its internal dynamics for Paul traps. This is done by considering both the internal state's Hamiltonian  (where σ is the Pauli matrix and
(where σ is the Pauli matrix and  is the energy gap between the ground and excited state), the motional Hamiltonian
is the energy gap between the ground and excited state), the motional Hamiltonian 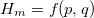 as a function of the position and momentum operator, and letting there be a coupling between them by modeling it as a classical field interacting with a two-level system in a rotating wave approximation [36],
as a function of the position and momentum operator, and letting there be a coupling between them by modeling it as a classical field interacting with a two-level system in a rotating wave approximation [36],

where g denotes the coupling between the internal state and motional degree of freedom, k is the wave vector of the field with frequency 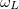 . The internal state can be readout as discussed in refs. [36,37], letting one obtain the state of the continuous variable field state that corresponds to the motional degree of freedom. Such determination of the field's state is known as quantum state endoscopy [37,38]. Another way to do the measurement is by a quantum non-demolition (QND) measurements. With a different coupling between the internal state and the motional degree of freedom [39],
. The internal state can be readout as discussed in refs. [36,37], letting one obtain the state of the continuous variable field state that corresponds to the motional degree of freedom. Such determination of the field's state is known as quantum state endoscopy [37,38]. Another way to do the measurement is by a quantum non-demolition (QND) measurements. With a different coupling between the internal state and the motional degree of freedom [39],

where 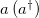 represents the annihilation (creation) operator on the motion degree of freedom such that
represents the annihilation (creation) operator on the motion degree of freedom such that  and
and  ,
,  is the z component of the Pauli matrix for the j-th ion, representing its internal state, and χ represents the coupling strength. In a classical laser driving,
is the z component of the Pauli matrix for the j-th ion, representing its internal state, and χ represents the coupling strength. In a classical laser driving, 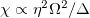 , where η is the Lamb-Dicke parameter, Ω is the Rabi frequency for the ion's internal state, Δ is the detuning. This scheme can let one determine the vibrational quantum number of the lowest normal mode of the ions: due to the coupling above, the motional state of the ions can be entangled with the internal states of the ions. By design, this measurement strategy reads out the internal state of the ions in a designated order. Denoting the results of the internal state as 1 for excited and 0 for ground state, the record of the measurement can be interpreted as a binary number which encodes an integer n. By subjecting the output state to
, where η is the Lamb-Dicke parameter, Ω is the Rabi frequency for the ion's internal state, Δ is the detuning. This scheme can let one determine the vibrational quantum number of the lowest normal mode of the ions: due to the coupling above, the motional state of the ions can be entangled with the internal states of the ions. By design, this measurement strategy reads out the internal state of the ions in a designated order. Denoting the results of the internal state as 1 for excited and 0 for ground state, the record of the measurement can be interpreted as a binary number which encodes an integer n. By subjecting the output state to  after the simulation is done, this strategy may offer one possible way to read out the motional (continuous variable) state through measuring the internal state which is discrete. Assuming one can do Fourier transform on the internal state for all ions, this result can signal a normal mode of the quantum number n of the motional degree with the same probability, thus allowing one to obtain the properties of the motional state by reading out the internal two-level states. In addition, one may also use an imaging technique to measure the position of the ions [40] in the trap.
after the simulation is done, this strategy may offer one possible way to read out the motional (continuous variable) state through measuring the internal state which is discrete. Assuming one can do Fourier transform on the internal state for all ions, this result can signal a normal mode of the quantum number n of the motional degree with the same probability, thus allowing one to obtain the properties of the motional state by reading out the internal two-level states. In addition, one may also use an imaging technique to measure the position of the ions [40] in the trap.
Quantum simulation
Consider an interacting electron gas described by the Hamiltonian  [41]
[41]

where  is the electron mass and
is the electron mass and 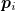 and
and 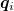 are the momentum and position operators, respectively, for the i-th electron. The first term represents the kinetic energy and the second term represents the potential energy resulting from mutual Coulomb interactions among the electrons. Because of the many-body nature of the problem, the Hilbert space grows exponentially with the number of electrons, making an exact solution of the Schrödinger equation difficult. Although in certain studies, only the average effect of the electrons is relevant and one may employ a mean field approximation, an exact analysis is still indispensable for a complete description. In addition, due to their small size, electrons can be very difficult to control and measure in a realistic experimental setting, making the study of this system both theoretically and experimentally challenging.
are the momentum and position operators, respectively, for the i-th electron. The first term represents the kinetic energy and the second term represents the potential energy resulting from mutual Coulomb interactions among the electrons. Because of the many-body nature of the problem, the Hilbert space grows exponentially with the number of electrons, making an exact solution of the Schrödinger equation difficult. Although in certain studies, only the average effect of the electrons is relevant and one may employ a mean field approximation, an exact analysis is still indispensable for a complete description. In addition, due to their small size, electrons can be very difficult to control and measure in a realistic experimental setting, making the study of this system both theoretically and experimentally challenging.
Rather than directly solving for the Hamiltonian equation (4), we found a way [23] to simulate this electronic system with a different quantum system using ions, which also includes the standard kinetic term with a repulsive Coulomb interaction when the ions all carry positive or negative charges. The advantage of using ion-based systems is that they can be much more experimentally accessible due to the rapid advances made in the field of trapped ions. A typical quantum simulation consists of three stages:
- 1)Initialization: preparation of an initial state.
- 2)Evolution: time evolution under either blocks of qubit gates (digital simulation), or a specifically engineered Hamiltonian (analog simulation).
- 3)Measurement: readout of the result.
Assuming the quantum simulator to be well controlled experimentally, the most critical task is to design the required propagator, so that a map exists between the initial and final states of the simulator and those of the system under consideration [6].
To simulate the electron gas, consider a box loaded with N identical ions with repulsive Coulomb interactions, with the Hamiltonian reading

where  is the mass of the ion and Q is the degree of ionization. The trapped ion Hamiltonian equation (5) is formally similar to the electronic one, eq. (4), but there are significant differences. The ion to electron mass ratio is on the order of
is the mass of the ion and Q is the degree of ionization. The trapped ion Hamiltonian equation (5) is formally similar to the electronic one, eq. (4), but there are significant differences. The ion to electron mass ratio is on the order of  for ions such as
for ions such as  or
or  commonly used in experiments, and degree of ionization Q may be greater than 1. Since the kinetic term and the Coulomb interaction terms do not commute, these disparities rule out direct use of ions as an analog simulator for this problem. However, there exists a unitary mapping that can map the electronic system onto the ion based one. The map is a rotation described by the unitary dilatation operator [42]
commonly used in experiments, and degree of ionization Q may be greater than 1. Since the kinetic term and the Coulomb interaction terms do not commute, these disparities rule out direct use of ions as an analog simulator for this problem. However, there exists a unitary mapping that can map the electronic system onto the ion based one. The map is a rotation described by the unitary dilatation operator [42]

where  , and rk are taken to be real-valued dilatation parameters for the k-th particle. Using the Baker-Campbell-Hausdorff (BCH) formula [43]
, and rk are taken to be real-valued dilatation parameters for the k-th particle. Using the Baker-Campbell-Hausdorff (BCH) formula [43]

where ![$[_m A,B]=[A,[_{m-1} A,B]]$](https://content.cld.iop.org/journals/0295-5075/130/1/10001/revision1/epl20097ieqn24.gif) and
and ![$[_1 A,B]=[A,B]$](https://content.cld.iop.org/journals/0295-5075/130/1/10001/revision1/epl20097ieqn25.gif) is the commutator, one finds that for the k-th particle the position and momentum operators transform as
is the commutator, one finds that for the k-th particle the position and momentum operators transform as

Thus, the dilatation transform scales the momentum and position terms differently, allowing the ratio between the two terms in the Hamiltonian (eq. (5)) to be tuned so that one can match the Hamiltonian of the electronic system with the ion-based one. We use identical ions to simulate the identical electrons, therefore 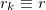 for
for  and denote the corresponding dilatation transform as S(r). Due to the unitary nature of S(r),
and denote the corresponding dilatation transform as S(r). Due to the unitary nature of S(r),

for any operator functions fk. Therefore, for the Hamiltonian of the simulator

where  represents the effective mass after the dilatation. Then, by requiring
represents the effective mass after the dilatation. Then, by requiring  , the e-e Hamiltonian in eq. (4) is recovered exactly, with
, the e-e Hamiltonian in eq. (4) is recovered exactly, with ![$r = \log[Q^2 m_{\rm ion}/m_{\rm e}]$](https://content.cld.iop.org/journals/0295-5075/130/1/10001/revision1/epl20097ieqn30.gif) ,
,

This relation fixes the dilatation parameter r and the scaled runtime  . Note that the choice of the ion alone uniquely determines the dilatation parameter r. It is also easy to prove that for the electron gas propagator
. Note that the choice of the ion alone uniquely determines the dilatation parameter r. It is also easy to prove that for the electron gas propagator

where  and
and 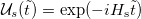 is the propagator for the simulator.
is the propagator for the simulator.
Therefore, we have established a one-to-one mapping between the initial state 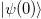 of the interacting electrons and the initial state
of the interacting electrons and the initial state 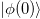 of the quantum simulator, as well as between the corresponding final states
of the quantum simulator, as well as between the corresponding final states 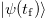 and
and  . This, in turn, enables the quantum simulation of the e-e Coulomb interactions using ions. Our approach is exact and does not impose a limit on the dimensions or incorporate any approximations such as mean-field theory. Additionally, the same idea can be extended to tune the ratio between the coefficients before the position-dependent term and the momentum-dependent term in other Hamiltonians.
. This, in turn, enables the quantum simulation of the e-e Coulomb interactions using ions. Our approach is exact and does not impose a limit on the dimensions or incorporate any approximations such as mean-field theory. Additionally, the same idea can be extended to tune the ratio between the coefficients before the position-dependent term and the momentum-dependent term in other Hamiltonians.
This mapping induces a corresponding rescaling of time for the propagator. The dilatation parameter and the new time scale are determined solely by the mass ratio between the ion and electron, and the degree of ionization. Additionally, since the mass of the electron is much less than that of the ions and  , we have
, we have 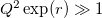 . Therefore, to simulate the propagator U(t) the simulator runtime
. Therefore, to simulate the propagator U(t) the simulator runtime 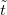 is much less than the physical runtime t. Since the quantumness of physical system can be quite fragile due to the inevitable coupling between the system and its environment, which can cause decoherence, this efficiency is quite beneficial since shorter runtimes decrease the susceptibility of the quantum simulator to such external noise and decoherence. It is worth pointing out that since the charge-mass ratio of the electrons is a constant, the choice of the ion alone determines the dilatation parameter r. However, this dilatation parameter only determines how the runtimes for the ion and electronic systems relate to each other and does not restrict the total runtime in an experiment. In a realistic setting, since the detection time is non-instantaneous, one needs to determine how to choose the runtime and how to carry out the measurement so that a reasonable time resolution can be achieved. This means that enough data points can be collected during the runtime for the subsequent Fourier transform in order to obtain the system's spectral information.
is much less than the physical runtime t. Since the quantumness of physical system can be quite fragile due to the inevitable coupling between the system and its environment, which can cause decoherence, this efficiency is quite beneficial since shorter runtimes decrease the susceptibility of the quantum simulator to such external noise and decoherence. It is worth pointing out that since the charge-mass ratio of the electrons is a constant, the choice of the ion alone determines the dilatation parameter r. However, this dilatation parameter only determines how the runtimes for the ion and electronic systems relate to each other and does not restrict the total runtime in an experiment. In a realistic setting, since the detection time is non-instantaneous, one needs to determine how to choose the runtime and how to carry out the measurement so that a reasonable time resolution can be achieved. This means that enough data points can be collected during the runtime for the subsequent Fourier transform in order to obtain the system's spectral information.
When boundary or finite-size effects of the system are required, the dilatation parameter also forces the same mapping between the boundaries of the electronic system and the boundary of the box confining the ions. For example, the dilatation transform maps a hard-wall boundary of width w for the electron gas

to a hard wall boundary of width  for the box. A similar scaling applies to any external potential, and the explicit function form is given by
for the box. A similar scaling applies to any external potential, and the explicit function form is given by 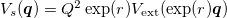 , where Vs and
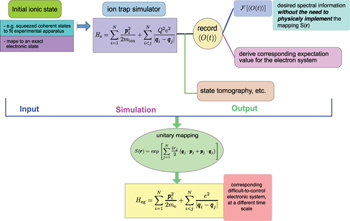
, where Vs and 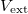 are the potentials for the simulator and electron gas, respectively. In fig. 1 we show a schema of our proposal. The input, unitary evolution and output of the simulator are tied to the corresponding electron system through a unitary transform.
are the potentials for the simulator and electron gas, respectively. In fig. 1 we show a schema of our proposal. The input, unitary evolution and output of the simulator are tied to the corresponding electron system through a unitary transform.
Fig. 1: Schematic representation of the quantum simulation discussed in this work. We start with an initial state of the ion-based simulator, which evolves under Hs. For the read-out, we can keep the record of and observable O to build its record, which will give us the desired information after a Fourier transform. If only energy spectra are needed, no additional complexity overhead is added in that it is unnecessary to simulate the dilatation operation on the simulator explicitly. We may also do quantum state tomography if the details of the wave function are required, which can be mapped back to the electronic system following the same dilatation transform.
Download figure:
Standard imageAnother advantage of using this unitary transform as the mapping between the electronic and ionic system is that even in the case where the simulation of an exact electronic state is needed, we still may not need to physically implement the dilatation operation. We only require a different initialization routine and the observables of the simulated system are a simple function of the readout results. To see this, consider the case where the initial electronic state is a coherent state  for the i-th electron, and one needs to record either the position xi or the momentum pi (or, some function of the position/momentum) of the electrons. The coherent state is widely used in experiments. Defined as the eigenstates of the bosonic annihilation operator a with an eigenvalue of α, the coherent state may be generated from the vacuum state. Written in terms of the bosonic creation and annihilation operators, the displacement operator and the dilatation operator are given by
for the i-th electron, and one needs to record either the position xi or the momentum pi (or, some function of the position/momentum) of the electrons. The coherent state is widely used in experiments. Defined as the eigenstates of the bosonic annihilation operator a with an eigenvalue of α, the coherent state may be generated from the vacuum state. Written in terms of the bosonic creation and annihilation operators, the displacement operator and the dilatation operator are given by ![$D(\alpha) = \exp [\alpha a^\dagger-\alpha^* a]$](https://content.cld.iop.org/journals/0295-5075/130/1/10001/revision1/epl20097ieqn45.gif) and
and ![$S(r) = \exp [\frac{r}{2}(a^2-a^\dagger {}^2)]$](https://content.cld.iop.org/journals/0295-5075/130/1/10001/revision1/epl20097ieqn46.gif) , respectively, where we have used
, respectively, where we have used 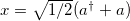 ,
,  . The coherent state
. The coherent state 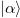 may be thus generated from
may be thus generated from  .
.
As an example, let us consider a position measurement record for the electronic system 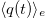 , it can be readily shown
, it can be readily shown

where  is the unitary propagator, the subscript e(s) corresponds to the electronic system and the simulator, respectively, and the average for the simulator is for an initial squeezed coherent state
is the unitary propagator, the subscript e(s) corresponds to the electronic system and the simulator, respectively, and the average for the simulator is for an initial squeezed coherent state  . This shows that the position measurement record on the simulator relates to the electronic system data by a rescaled time
. This shows that the position measurement record on the simulator relates to the electronic system data by a rescaled time 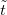 and an overall scaling factor of er. Therefore, given the simulator measurement data, one can easily do post-processing and recover the corresponding measurement data for the electronic system. Furthermore, we can utilize the unitary nature of the dilatation operator to show that one does not need to physically implement this operation, just a small overhead of preparing a squeezed state can suffice, which can be done for the trapped ions [44]. For a squeezing operator acting on an electronic coherent initial state, denote
and an overall scaling factor of er. Therefore, given the simulator measurement data, one can easily do post-processing and recover the corresponding measurement data for the electronic system. Furthermore, we can utilize the unitary nature of the dilatation operator to show that one does not need to physically implement this operation, just a small overhead of preparing a squeezed state can suffice, which can be done for the trapped ions [44]. For a squeezing operator acting on an electronic coherent initial state, denote 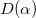 as the displacement operator and
as the displacement operator and  as the vacuum state,
as the vacuum state,

i.e., a displacement operator with a different parameter, acting on a squeezed state 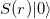 . Using the Baker-Campbell-Hausdorff (BCH) formula (7), it can be shown that
. Using the Baker-Campbell-Hausdorff (BCH) formula (7), it can be shown that

i.e., with a mapping  . Following this procedure, the mapping for other initialization schemes
. Following this procedure, the mapping for other initialization schemes 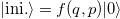 can be easily derived. This shows that when the exact electronic state to be simulated can be initialized by acting with some operator on a vacuum state, the complexity overhead of using trapped ions to simulate lies only in the preparation of a squeezed state, which has been shown to be feasible [44].
can be easily derived. This shows that when the exact electronic state to be simulated can be initialized by acting with some operator on a vacuum state, the complexity overhead of using trapped ions to simulate lies only in the preparation of a squeezed state, which has been shown to be feasible [44].
In addition, if we could couple the simulator to a quantum circuit capable of generating a controlled-U operation, which takes in a qubit state as control and applies the unitary operation on the wave function only if the control qubit is in  , a more general way to obtain the spectrum can be used, namely the quantum phase estimation algorithm [45–47], which can give us the energy eigenvalues. This technique has been reported for the ground-state energy of the ground-state energy in molecular systems [48]. For an estimate of the phase up to n-bit precision, the standard quantum phase estimation algorithm with quantum Fourier transforms may be readily used.
, a more general way to obtain the spectrum can be used, namely the quantum phase estimation algorithm [45–47], which can give us the energy eigenvalues. This technique has been reported for the ground-state energy of the ground-state energy in molecular systems [48]. For an estimate of the phase up to n-bit precision, the standard quantum phase estimation algorithm with quantum Fourier transforms may be readily used.
Discussion: restrictions of the proposed approach
While the interacting free electrons and interacting ions obey formally similar Hamiltonians containing a kinetic term and a Coulomb interaction term, there exists a disparity between the masses of electrons and ions, as well as the different charges the ions may carry, which preclude the possibility of a direct simulation. Here, we mathematically prove that through a dilatation transform, the propagator of the electron system at time t gives a spectrum that is mapped one to one to the spectrum of the simulator at a rescaled time 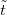 , with the scaling factor between
, with the scaling factor between  and t specified completely by the mass of the ion and its degree of ionization. Since the trapped ions are much more experimentally accessible than the electrons, this map enables the implementation of a quantum simulator to study the Coulomb interactions in an electron gas by using trapped ions that is also dimension- agnostic.
and t specified completely by the mass of the ion and its degree of ionization. Since the trapped ions are much more experimentally accessible than the electrons, this map enables the implementation of a quantum simulator to study the Coulomb interactions in an electron gas by using trapped ions that is also dimension- agnostic.
To actually implement the quantum simulator, there are certain requirements one would need to satisfy. For example, one needs to confine the ions and design a corresponding measurement scheme for some physical quantity O, e.g., with the help of Fresnel lenses [49], to build a history of the positions [50,51]. Then our proposal ensures that a subsequent Fourier transformation will give the spectral information of the electron system without any additional experimental complexity because the map is unitary. In this case, it is worth pointing out that one is free to choose any appropriate initialization for the quantum simulation based on the experimental equipment. However, it can be different for the case where the dynamics of the wave function is also needed, where only a simple unitary rotation on the initial state is necessary for the initialization, which has been suggested for trapped ions [44]. Moreover, the rescaled runtime of the simulator is shorter than the timescale for the evolution of the electron gas, minimizing the susceptibility of the quantum simulator to external noise and decoherence.
Conclusions
We reviewed a strategy to use trapped ions as an analog quantum simulator to study the many-body Coulomb electron-electron interactions. Due to the exponential growth of the Hilbert space for many-body quantum systems as the number of particles grows, the electron gas system is difficult to deal with theoretically without approximations. Additionally, due to the non-commutative nature of the position and momentum dependent terms, a direct simulation of the electronic system with an ion-based one is not possible, therefore an appropriate mapping between the two systems needs to be found. Here, this mapping is provided by a unitary dilatation operator, and the ion-based system is then able to simulate the e-e Coulomb interaction at a different time scale. Since the mapping is unitary, it does not change the spectrum of the system and thus comes with no complexity overhead if only the spectral information is required. We also discuss state initialization with squeezed coherent states and more generic readout in the form of a quantum phase estimation procedure.
To generalize our proposal, a straightforward extension is to incorporate different geometries on the confined ions, such as chains [16], rings [52], or even periodical optical lattices [53,54]. Particularly, when the ions are loaded in a two-dimensional honeycomb lattice, the quantum simulator can emulate the electrons in graphene-like structures, allowing massless Dirac quasi-particles and its topological phases to be studied [24].
This technique can be easily extended to many other interesting systems with different position and momentum dependence,

so long as  , to solve the problem of scaling difference between the momentum-dependent and position-dependent terms. More complex functional dependence like
, to solve the problem of scaling difference between the momentum-dependent and position-dependent terms. More complex functional dependence like  may also be considered.
may also be considered.
Acknowledgments
L-AW is supported by the Basque Country Government (Grant No. IT986-16) and PGC2018-101355-B-I00 (MCIU/AEI/FEDER, UE).