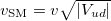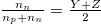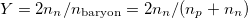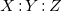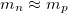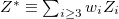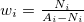Abstract
We derive the ratio of dark energy to baryon matter content in the universe from a Higgs potential matching a description of baryon matter on an intrinsic configuration space. The match determines the Higgs mass and self-coupling parameters and introduces a constant term in the Higgs potential. The constant term is taken to give dark energy contributions from detained neutrons, both primordial and piled-up neutrons from nuclear processes in stars. This corresponds to the dark energy content increasing with time. The two contributions possibly give rise to the primordial inflation and the later accelerated recession, respectively. The ensuing inflation during nucleosynthesis may explain the primordial lithium-seven deficit relative to the standard Big Bang nucleosynthesis model predictions. From the observed helium and stellar metallicity contents, we get a dark energy to baryon matter ratio of 14.5(0.7) to compare with the observed value of 13.9(0.2).
Export citation and abstract BibTeX RIS

Published by the EPLA under the terms of the Creative Commons Attribution 3.0 License (CC-BY). Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.
Introduction
Observation of accelerated recession of supernovae in low and high red-shift galaxies [1] led to the acceptance of a major dark energy content in the universe [2,3]. The present, observed ratio  [4] between the dark energy content and the baryonic content remains unexplained. We suggest that the dark energy content of the universe is a manifestation of detained neutron decay, expressed as a constant term in the Higgs potential. We derive the ratio
[4] between the dark energy content and the baryonic content remains unexplained. We suggest that the dark energy content of the universe is a manifestation of detained neutron decay, expressed as a constant term in the Higgs potential. We derive the ratio  from an intrinsic conception of the structural changes taking place during transformations between protons and neutrons in the nuclear fusion processes inside stars. The present work is developed from [5]. We leave the question unanswered as to how the underlying coupling to accelerated expansion should be described. Suggestions already exist concerning the relation between Higgs physics, inflation and dark energy, mediated by a coupling between the Higgs field and the Ricci curvature of spacetime [6–10]. The problem in these models is to find a "natural" coupling level. Also models with add-on inflaton fields have been considered [11]. The accelerated supernovae recession has been called into question [12] as dependent on bias removal from observational samples. The biases concern the choice of coordinate system, removal of peculiar velocities with respect to the cosmic microwave background and possible red-shift and light curve bias for the supernovae analyzed. The debate [13,14] has made it clearer than ever that determinations of cosmological parameters is a combination of observations and models. Fluctuations in radiation and matter distributions as inferred from fluctuations in the cosmic microwave radiation (CMB) and from baryon acoustic oscillations (BAO) inferred from galaxy clustering can be modelled by a cosmological model ΛCDM with a cosmological constant and a cold dark matter component to add up to a more or less flat universe [4].
from an intrinsic conception of the structural changes taking place during transformations between protons and neutrons in the nuclear fusion processes inside stars. The present work is developed from [5]. We leave the question unanswered as to how the underlying coupling to accelerated expansion should be described. Suggestions already exist concerning the relation between Higgs physics, inflation and dark energy, mediated by a coupling between the Higgs field and the Ricci curvature of spacetime [6–10]. The problem in these models is to find a "natural" coupling level. Also models with add-on inflaton fields have been considered [11]. The accelerated supernovae recession has been called into question [12] as dependent on bias removal from observational samples. The biases concern the choice of coordinate system, removal of peculiar velocities with respect to the cosmic microwave background and possible red-shift and light curve bias for the supernovae analyzed. The debate [13,14] has made it clearer than ever that determinations of cosmological parameters is a combination of observations and models. Fluctuations in radiation and matter distributions as inferred from fluctuations in the cosmic microwave radiation (CMB) and from baryon acoustic oscillations (BAO) inferred from galaxy clustering can be modelled by a cosmological model ΛCDM with a cosmological constant and a cold dark matter component to add up to a more or less flat universe [4].
Our purpose here is only to give a derivation from theoretical considerations of the present value of the dark energy to baryon matter content. If our derivation is causally correct, it means that the dark energy content increases with time from its primordial value after nucleosynthesis, followed by the pile-up of neutrons in stellar burning of nuclear fuel, e.g., neutrons in helium nuclei in the p-p cycle in main sequence stars. That is, burning hydrogen to helium with the gross result

where new neutrons are detained in the helium nuclei.
Dark energy and Higgs potential
We repeat the Higgs potential [15] from [16], also used in [17] for Higgs couplings to gauge bosons

with Higgs field ϕ [18–21] and coefficients

expressed in the electroweak energy scale 

Here  is a baryonic energy scale [16,22] not to be confused with the cosmological constant. Further,
is a baryonic energy scale [16,22] not to be confused with the cosmological constant. Further,  and
and 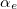 are the fine structure couplings at the W boson and electron energy scales respectively1
.
are the fine structure couplings at the W boson and electron energy scales respectively1
.
The Higgs mechanism mediates the electroweak neutron to proton transformation with Higgs field 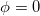 for a neutronic state and
for a neutronic state and 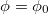 for a protonic state, see fig. 1. Reversing the mechanism, we thus assume, that for each detained neutron there is one zero-mode δ-contribution to the dark energy. With
for a protonic state, see fig. 1. Reversing the mechanism, we thus assume, that for each detained neutron there is one zero-mode δ-contribution to the dark energy. With  from (3), this gives the following dark energy to baryon matter ratio:
from (3), this gives the following dark energy to baryon matter ratio:

Here the n's are cosmological number densities of the respective species and the baryons we consider are either neutrons or protons, i.e.,  . The ratio
. The ratio  for use as
for use as  in (5) we get from the helium Y and heavier Z content by the expression (see, e.g., p. 481 in [23])
in (5) we get from the helium Y and heavier Z content by the expression (see, e.g., p. 481 in [23])

Here  is weighted with relative neutron content in each nucleus2
. Then, in standard model language where
is weighted with relative neutron content in each nucleus2
. Then, in standard model language where 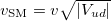 [17] and with
[17] and with  from (4), we get by insertion in (5)
from (4), we get by insertion in (5)

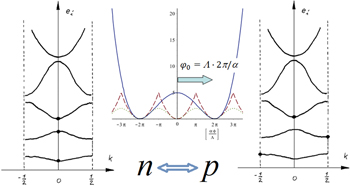
Fig. 1: The nucleon transformation 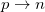 in stars burning hydrogen to helium (and so forth) is manifested in the Higgs potential with a non-zero value at
in stars burning hydrogen to helium (and so forth) is manifested in the Higgs potential with a non-zero value at 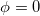 . We interpret the non-zero value of the Higgs potential from each detained neutron in nuclei as a contribution to the dark energy content in the universe. Left and right: reduced zone schemes (see, e.g., p. 160 in [24]) for Bloch wave numbers for the neutron state (left) and the proton state (right) in solutions of (19) with, respectively,
. We interpret the non-zero value of the Higgs potential from each detained neutron in nuclei as a contribution to the dark energy content in the universe. Left and right: reduced zone schemes (see, e.g., p. 160 in [24]) for Bloch wave numbers for the neutron state (left) and the proton state (right) in solutions of (19) with, respectively,  and
and  periodic wave functions [16]. Middle: Higgs potential (solid, blue) matching the Manton-inspired potential [25] (dashed, red) and the Wilson-inspired potential [26] (dotted, green). The Manton- and Wilson-inspired potentials yield the same value for the Higgs mass and the electroweak energy scale whereas only the Manton-inspired potential gives a satisfactory reproduction of the baryon spectrum [16,27]. Figure adapted from [28].
periodic wave functions [16]. Middle: Higgs potential (solid, blue) matching the Manton-inspired potential [25] (dashed, red) and the Wilson-inspired potential [26] (dotted, green). The Manton- and Wilson-inspired potentials yield the same value for the Higgs mass and the electroweak energy scale whereas only the Manton-inspired potential gives a satisfactory reproduction of the baryon spectrum [16,27]. Figure adapted from [28].
Download figure:
Standard imageAs an example we here used  [29] from a globular cluster as a representative of a stellar population and set
[29] from a globular cluster as a representative of a stellar population and set  which is the metallicity for our own Sun. Our Sun has
which is the metallicity for our own Sun. Our Sun has  in the bulk [30] with X being the hydrogen fraction and Z is the fraction of elements with atomic number larger than 2 for helium. Further we used
in the bulk [30] with X being the hydrogen fraction and Z is the fraction of elements with atomic number larger than 2 for helium. Further we used 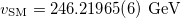 ,
, 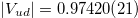 and
and  [4]. The value of the standard model electroweak energy scale
[4]. The value of the standard model electroweak energy scale 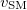 is obtained from the Fermi coupling constant
is obtained from the Fermi coupling constant 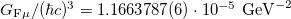 [4] by
[4] by 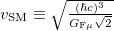 . The dark energy to baryonic matter value in (7) agrees with the observed ratio [4], see fig. 2,
. The dark energy to baryonic matter value in (7) agrees with the observed ratio [4], see fig. 2,

Fig. 2: Dark energy to baryon matter ratio  for our model as represented by eq. (7) using a representative Y [29] (dotted green) and adding the solar Z from its bulk [30] (dashed red) compared with the observed ratio (8) (solid blue) [4]. The curves show Gaussian uncertainty distributions around mean values μ with standard deviations σ. Our model assumes the dark energy to reside in the Higgs potential with a constant contribution for every neutron detained in atomic nuclei as they are left over from the primordial nucleosynthesis and later pile up in the evolution of stars. This means that we expect the dark energy content to increase with time, primarily from the burning of hydrogen to helium (and so forth) in main sequence stars.
for our model as represented by eq. (7) using a representative Y [29] (dotted green) and adding the solar Z from its bulk [30] (dashed red) compared with the observed ratio (8) (solid blue) [4]. The curves show Gaussian uncertainty distributions around mean values μ with standard deviations σ. Our model assumes the dark energy to reside in the Higgs potential with a constant contribution for every neutron detained in atomic nuclei as they are left over from the primordial nucleosynthesis and later pile up in the evolution of stars. This means that we expect the dark energy content to increase with time, primarily from the burning of hydrogen to helium (and so forth) in main sequence stars.
Download figure:
Standard imageIn table 1 we show determinations of both primordial helium content Yp and evolved contents Y determined by different methods. It is clear that the values vary and therefore the numerical result in (7) must be taken with reservation. Taken at face value, eq. (7) compared to (8) suggests that zero-mode δ-contributions from the Higgs field could constitute the present estimate of the dark energy in the universe.
Table 1:. Helium content in the universe. We list various determinations of the helium content from a standard Big Bang Nucleosynthesis prediction (BBN, Pitrou et al.) [36], HII-regions (HII, Izokov et al.) [32], intergalactic clouds (IGC, Cooke and Fumagalli) [33], cosmic microwave background (CMB, Henning et al., Ade et al., Keisler et al., Guo and Zhang) [34–35], [37–38], our Sun (Sun, Asplund et al.) [30], globular clusters (GC, Villanova et al., Nardiello et al., Milone) [29,31,39] and globular clusters in the Small Magellanic Cloud (SMC, Lagioia et al.) [40].
| Source | Value | Reference |
|---|---|---|
| BBN | 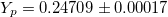 |
[36] |
| HII |  |
[32] |
| IGC | 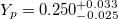 |
[33] |
| CMB |  |
[37] |
| CMB |  |
[38] |
| CMB | 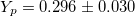 |
[34] |
| CMB |  |
[35] |
| Sun |  |
[30] |
| GC | 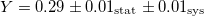 |
[29] |
| GC | 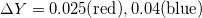 |
[29] |
| GC | 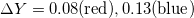 |
[31] |
| GC | 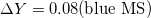 |
[39] |
| SMC | 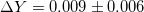 |
[40] |
| SMC | 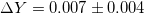 |
[40] |
| SMC |  |
[40] |
| SMC | 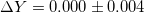 |
[40] |
(a)Planck 2015 [38] states various determinations. The value shown here is determined by treating Yp as a free parameter in a Big Bang Nucleosynthesis model.
Helium content in the universe
Determinations of the helium fraction Y in the universe is an active field in astrophysics. Investigations look for variations in different star populations within a specific globular cluster or dwarf galaxies like the Small Magellanic Cloud or they look for ways to determine the primodial helium fraction Yp, i.e., the fraction immediately after the nucleosynthesis in the first minutes after Big Bang.
What is of concern to us here is the relation between age and helium plus metallicity fraction. The determination of the helium content in stars is based on observation of the intensity of absorption lines in the spectrum of the stars. The determination of star age is based on models for nuclear fusion in stars. These models lead to the result that more massive stars generally evolve quicker, they burn quicker by fusion due to a higher pressure and therefore higher temperature in their interior leading to increased fusion rates. With higher temperature follows a higher colour temperature in the light shining from the star. On the average therefore one would expect a higher helium fraction in blue stars than in red stars. That indeed is what is observed, see, e.g., [31] which finds helium enhancements 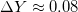 for red stars and
for red stars and 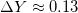 for blue stars. We may therefore trust that increasing helium fraction in stars is a measure of increasing evolution age. We are aware that this argument relates to main sequence stars in the Hertzsprung-Russell diagram, see, e.g., p. 181 in [23]. Very heavy stars —and old stars— may be so dense from gravitational contraction that they start burning helium. This of course diminishes the helium content in the stellar interior and ultimately in the star's atmosphere. One would therefore need to include
for blue stars. We may therefore trust that increasing helium fraction in stars is a measure of increasing evolution age. We are aware that this argument relates to main sequence stars in the Hertzsprung-Russell diagram, see, e.g., p. 181 in [23]. Very heavy stars —and old stars— may be so dense from gravitational contraction that they start burning helium. This of course diminishes the helium content in the stellar interior and ultimately in the star's atmosphere. One would therefore need to include 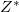 in the calculation based on (7). The same goes for main sequence stars when nearing the end of their lives. Indeed, our own Sun is expected to start burning helium when the hydrogen in its centre has already been transformed.
in the calculation based on (7). The same goes for main sequence stars when nearing the end of their lives. Indeed, our own Sun is expected to start burning helium when the hydrogen in its centre has already been transformed.
The primordial helium fraction Yp can be extracted in various ways. One can analyse spectra from HII-regions in galactic mediae containing a mixture of helium and hydrogen that is supposed not yet to have participated in fusion processes in stars —one looks for He emission lines [32]. Or one can look for absorption lines in the spectrum of a distant quasar whose light passes through intergalactic gas clouds [33] likewise thought not to have been involved in fusion in stars. And one can analyse the cosmic microwave background for diminished fluctuations in the damping tail of the power spectrum [34,35]. The latter method is somewhat model-dependent. It takes as granted a relation between Yp and the number density of free electrons ne and baryons nb at the time of hydrogen recombination [35]

Here it is assumed that the helium recombination happens much earlier than the hydrogen recombination from which the cosmic microwave background radiation originates. The larger the Yp, the smaller ne and thus the less the photons interact with the not yet recombined primordial plasma. In short: the larger the Yp, the larger the photon mean-free path and thereby the smaller the damping tale power spectrum fluctuations in the cosmic microwave background [35].
In table 1 we list various determinations of the helium content, both Yp and Y and variations in their determinations. From table 1 we see that the determinations of Yp are converging around the value predicted from a standard Big Bang Nucleosynthesis model [36]. Using, e.g., Yp from HII in (7) would give 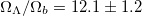 which is somewhat lower than the observed value
which is somewhat lower than the observed value  . But we want to determine a present value for
. But we want to determine a present value for  from (7). Thus we need some kind of average
from (7). Thus we need some kind of average 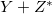 for the star population in the Milky Way and its surroundings within minimal red-shifts z in stead of the primordial value Yp. For this, the determinations from globular clusters could serve as representative where Villanova et al. find
for the star population in the Milky Way and its surroundings within minimal red-shifts z in stead of the primordial value Yp. For this, the determinations from globular clusters could serve as representative where Villanova et al. find 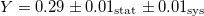 [29] for the globular cluster Messier 4 shown in fig. 3. This yields
[29] for the globular cluster Messier 4 shown in fig. 3. This yields  and is shown in fig. 2. To get an exemplar
and is shown in fig. 2. To get an exemplar  we added the solar Z for the result
we added the solar Z for the result 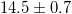 in (7) which agrees with the observed value
in (7) which agrees with the observed value  within uncertainties and also is shown in fig. 2. We repeat that there are large variations among star populations as seen already from table 1. One thing seems to be certain, though, namely the increase of the
within uncertainties and also is shown in fig. 2. We repeat that there are large variations among star populations as seen already from table 1. One thing seems to be certain, though, namely the increase of the 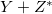 content with increasing star evolution in general. And that is what is key to our argument that we should expect
content with increasing star evolution in general. And that is what is key to our argument that we should expect 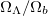 to increase with time from neutron pile-up in accordance with the observed accelerated recession of supernovae interpreted as originating in increasing dark energy content in the universe.
to increase with time from neutron pile-up in accordance with the observed accelerated recession of supernovae interpreted as originating in increasing dark energy content in the universe.
Fig. 3: The beautiful globular cluster Messier 4 (NGC 6121) used in [29] for determinations of helium content Y in different star populations. Blue stars are more evolved than red and show a larger helium content. From (7) and our conception of the Higgs mechanism in fig. 1, we expect the dark energy content of the universe to increase with stellar evolution due to pile-up of neutrons from nuclear fusion in the stars' interior. For each neutron detained in the nuclei of heavier elements we expect one zero-mode contribution δ from the Higgs potential (2). Image credit: NASA, STScI. Downloaded from https://commons.wikimedia.org/w/index.php?curid=4550051.
Download figure:
Standard imageDiscussion
We here discuss the cosmological constant as a manifestation of dark energy and we consider the possible contribution to dark matter from the electron neutrinos originating in the build up of neutrons in stars.
The field equations of general relativity with a cosmological constant Λ read (cf. p. 155 in [41])

where 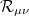 is the curvature tensor constructed from derivatives of the spacetime metric
is the curvature tensor constructed from derivatives of the spacetime metric 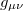 ,
, 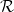 is the contraction of
is the contraction of  over the spacetime indices
over the spacetime indices 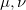 . On the right-hand side we have the total energy-momentum tensor
. On the right-hand side we have the total energy-momentum tensor 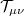 of matter and energy and
of matter and energy and 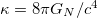 gives the strength of the influence of matter and energy on the metric on the left hand side. This strength is determined by Newton's constant of gravity GN and the speed of ligth c in empty space. Taking the cosmological term in (10) to the right-hand side
gives the strength of the influence of matter and energy on the metric on the left hand side. This strength is determined by Newton's constant of gravity GN and the speed of ligth c in empty space. Taking the cosmological term in (10) to the right-hand side

it interprets as a contribution to the energy-momentum tensor as first suggested by Gliner and Zeldovich, cf. p. 352 in [4].
Now consider the energy-momentum tensor of a scalar field ϕ (cf. p. 357 in [4])

The potential 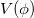 may have extrema where
may have extrema where 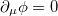 and where only
and where only 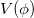 would survive as a contribution to the energy-momentum tensor. This is the standard way to derive a cosmological constant from a the potential of a scalar field [42], thus
would survive as a contribution to the energy-momentum tensor. This is the standard way to derive a cosmological constant from a the potential of a scalar field [42], thus

Comparing with (11), we see that 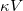 acts as a cosmological constant Λ. If we take ϕ to be the Higgs field, the potential
acts as a cosmological constant Λ. If we take ϕ to be the Higgs field, the potential  would be taken at its minimum value where ϕ equals its vacuum expectation value
would be taken at its minimum value where ϕ equals its vacuum expectation value 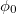 . One then expects the value of the potential to be of the order
. One then expects the value of the potential to be of the order 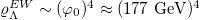 [42]. This would mean a huge value and the idea is only saved if
[42]. This would mean a huge value and the idea is only saved if  is zero. Actually for our
is zero. Actually for our 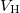 in (2) we have
in (2) we have 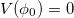 . Our potential was constructed to fit the intrinsic potential as seen in fig. 1 and therefore it was lifted to match to fourth order in ϕ the minima and curvature of the intrinsic potential. It is from this match we got the coefficients in (3). Now, there is one more stationary value where
. Our potential was constructed to fit the intrinsic potential as seen in fig. 1 and therefore it was lifted to match to fourth order in ϕ the minima and curvature of the intrinsic potential. It is from this match we got the coefficients in (3). Now, there is one more stationary value where 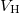 could contribute a constant value, namely at zero Higgs field where we get
could contribute a constant value, namely at zero Higgs field where we get

In (5) we used δ and 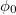 in units of energy. However, to be strict, we should include ℏ s and cs wherever appropriate to have correct field dimensions (cf. p. 357 in [43]) such that the potential gets the unit of energy per volume. Thus, writing out in full, we have
in units of energy. However, to be strict, we should include ℏ s and cs wherever appropriate to have correct field dimensions (cf. p. 357 in [43]) such that the potential gets the unit of energy per volume. Thus, writing out in full, we have

With 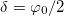 and
and  (see footnote 3
) from (3) inserted in (15) we get
(see footnote 3
) from (3) inserted in (15) we get

to substitute Λ in (11). This would still be at a patholigical value compared to the observed 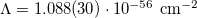 [4]. On the other hand, by allowing the Higgs field to stay at the unstable, stationary value
[4]. On the other hand, by allowing the Higgs field to stay at the unstable, stationary value 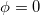 only when detained neutrons are present, we get a δ contribution to dark energy of the right order of magnitude as seen in (7). In the present view, the cosmological constant is not a constant as such but a spatial average over mostly zero values of the Higgs potential and the few locations where neutrons are present and δ takes the role of dark energy contributions. These contributions increase slowly with the pile-up of neutrons in stars.
only when detained neutrons are present, we get a δ contribution to dark energy of the right order of magnitude as seen in (7). In the present view, the cosmological constant is not a constant as such but a spatial average over mostly zero values of the Higgs potential and the few locations where neutrons are present and δ takes the role of dark energy contributions. These contributions increase slowly with the pile-up of neutrons in stars.
We know from observations towards our own Sun that the neutrinos from the p – p cycle in (1) escape the stars. It is thus of interest to evaluate such stellar neutrino contributions to the matter content of the universe. We infer the number density 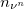 of such stellar "neutron-related" neutrinos (which may oscillate from e-type) to correspond to the build up of neutron density
of such stellar "neutron-related" neutrinos (which may oscillate from e-type) to correspond to the build up of neutron density 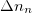 from stellar evolution, thus
from stellar evolution, thus

We take  and with
and with  and
and 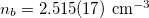 [4] this yields a contribution
[4] this yields a contribution

This is extremely minute compared to the total matter content of the universe 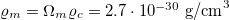 [4] including dark matter. The neutrinos from neutron pile-up inside stars considered here thus have essentially no decelerating effect on the universal expansion.
[4] including dark matter. The neutrinos from neutron pile-up inside stars considered here thus have essentially no decelerating effect on the universal expansion.
Baryon configurations
The basic dynamics and transformation mechanisms of our model are an intrinsic configuration space for protons and neutrons and the Higgs field absorbing phase changes among the wave functions involved in the electroweak transformations between these nucleons.
We have determined the three coefficients 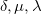 in (3) for the Higgs potential (2) in a common electroweak scale
in (3) for the Higgs potential (2) in a common electroweak scale 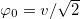 . The scale
. The scale 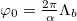 is determined via the baryonic energy scale
is determined via the baryonic energy scale  which happens to be close to the scale of quantum chromodynamics
which happens to be close to the scale of quantum chromodynamics 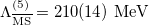 [4]. The scale
[4]. The scale  is set by a projection [22] of the intrinsic baryon dynamics to space. The length scale a for the projection is related to the classical electron radius
is set by a projection [22] of the intrinsic baryon dynamics to space. The length scale a for the projection is related to the classical electron radius 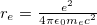 (see [44] and p. 97 in [45]) by the expression
(see [44] and p. 97 in [45]) by the expression 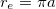 [22]. The factor π here manifests the toroidal shape of the intrinsic configuration space, the Lie group U(3), used for our description of baryons as stationary states of the Hamiltonian structure [22]
[22]. The factor π here manifests the toroidal shape of the intrinsic configuration space, the Lie group U(3), used for our description of baryons as stationary states of the Hamiltonian structure [22]

with configuration variable  , Laplacian Δ and a Manton-like trace potential [25]. The Hamiltonian structure in (19) is a reinterpretation of a Kogut-Susskind Hamiltonian [46] from Wilson's lattice gauge theory [26] for non-pertubative quantum chromodynamics. The trace potential in (19) folds out in periodic potentials in parameter space [47]. This opens for Bloch degrees of freedom with the Higgs mechanism as an agent, illustrated in fig. 1. The Bloch phase factors thus introduced lead to topological changes, e.g., from the charged protonic ground state with eigenvalue
, Laplacian Δ and a Manton-like trace potential [25]. The Hamiltonian structure in (19) is a reinterpretation of a Kogut-Susskind Hamiltonian [46] from Wilson's lattice gauge theory [26] for non-pertubative quantum chromodynamics. The trace potential in (19) folds out in periodic potentials in parameter space [47]. This opens for Bloch degrees of freedom with the Higgs mechanism as an agent, illustrated in fig. 1. The Bloch phase factors thus introduced lead to topological changes, e.g., from the charged protonic ground state with eigenvalue 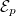 to a slightly increased value
to a slightly increased value  for the neutral neutron, right to left in fig. 1. The projection scaled by a led to a compact relation for the electron to neutron mass ratio [16,22]
for the neutral neutron, right to left in fig. 1. The projection scaled by a led to a compact relation for the electron to neutron mass ratio [16,22]

where  from a Rayleigh-Ritz solution [48,49] of (19) with 3078 base functions —at the limit of our computer programme. With the fine structure coupling
from a Rayleigh-Ritz solution [48,49] of (19) with 3078 base functions —at the limit of our computer programme. With the fine structure coupling 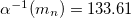 sliding by radiative corrections [28] from
sliding by radiative corrections [28] from 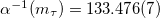 [4], eq. (20) yields
[4], eq. (20) yields

in agreement with the experimental value 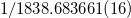 [4].
[4].
To sum up, the basic scale and coupling inputs of our model is the electron mass me and the fine structure coupling α. Provided we allow for α to slide to the relevant energy scales of the phenomena under study, we can condense higher-order field theory corrections into the value of the fine structure coupling as used, e.g., in (4).
Inflation and nucleosynthesis
It is beyond the scope of the present work to give a detailed discussion on primordial cosmology. However, a few notes seem in order. In Standard Big Bang Nucleosynthesis models [36] one starts from more or less equal neutron and proton abundances resulting from equilibrium with the neutrino bath in a radiation-dominated era preceeding the nucleosynthesis. One assumes negligible dark energy contributions and in so far as inflation is mentioned this phenomenon is thought to take place prior to the radiation era, see, e.g., [50]. It would be of interest though to consider a model where inflation is directly related to the neutron content. It would mean that inflation prior to the neutron-proton equilibrium would be already into its maximum because here the neutron content is a maximum. It would also mean that inflation would be still ongoing during nucleosynthesis, though at a slowing rate as the free neutrons decay during the cooling. And it would mean that dark energy would have to be included in the underlying spacetime description. One may worry that such a radical change could spoil the success of predicting Yp from Standard Big Bang Nucleosynthesis [36]. On the other hand, a continued inflation during synthesis will reduce the particle density and thereby reduce creation rates of nuclei past helium-4. This might solve the persisting Li-7 problem of a factor three too high prediction from Standard Big Bang Nucleosynthesis, see, e.g., [51]. The binding energy of nucleons in the helium-4 nucleus (the alpha particle) is considerable compared to the other light nuclei involved in the synthesis. Thus the alpha particle works already as an attractor in the network of mutual transitions among the primordial nuclei. It is therefore possible that the helium-4 fraction could remain more or less unaltered even in the case of inflation during synthesis.
Conclusion
We have found an expression for the ratio of dark energy to baryon matter content in the universe from a Higgs potential shaped by an intrinsic description of proton to neutron transformation. Our expression contains the cosmological neutron and proton densities and can be condensed into an expression containing the cosmic helium fraction and stellar metallicities as key ingredients. The vast majority of neutrons in the universe are bound in helium nuclei since primordial nucleosynthesis. We suggest the dark energy to represent detained neutrons and found our result by considering the helium and stellar metallicity content of baryon matter as determined in astrophysical observations. Our value 14.5(0.7) for the dark energy to baryon matter ratio compares well with the observed value 13.9(0.2). We look forward to improved determinations of the helium fraction and heavier elements in the baryon matter of the universe and to observations to determine whether the dark energy content is increasing with time as suggested by our interpretation.
Acknowledgments
I appreciated anonymous referee inquiries on the Higgs potential and on the neutrino contribution from neutron pile-up. I thank the Technical University of Denmark for an inspiring working environment. I thank my colleagues Henrik G. Bohr and Mogens S. Jensen for helpful discussions on the intrinsic viewpoint. In particular I thank Mogens S. Jensen for comments on the Higgs field operator.
Footnotes
- 1
Note that our v is related to the standard model value by
 via the up-down quark mixing matrix element Vud [17].
via the up-down quark mixing matrix element Vud [17]. - 2
In the left of eq. (6) we assume a 1:1 amount of neutrons and protons in the nuclei of all elements from helium and up. A simple counting argument then gives
 . This is most easily seen for Z = 0, where
. This is most easily seen for Z = 0, where  and all neutrons are detained in helium-4 nuclei. Then by definition of Y as a ratio of helium mass to the total, we count 2 units of the neutron number density nn into the helium mass contribution because helium-4 contains as many protons as it contains neutrons, i.e.,
and all neutrons are detained in helium-4 nuclei. Then by definition of Y as a ratio of helium mass to the total, we count 2 units of the neutron number density nn into the helium mass contribution because helium-4 contains as many protons as it contains neutrons, i.e.,  . For this counting it is essential that
. For this counting it is essential that  are mass ratios, that nuclear binding energies are small compared to the nuclear masses and that
are mass ratios, that nuclear binding energies are small compared to the nuclear masses and that  . The fact that, for heavy nuclei nn > np, modifies the implied
. The fact that, for heavy nuclei nn > np, modifies the implied  . The modification is done by substituting Z in the left eq. (6) with the weighted value
. The modification is done by substituting Z in the left eq. (6) with the weighted value  . Here Zi is the contribution from element i to the total metallicity and the weights count the neutron to proton ratio in the nucleus of this element, i.e.,
. Here Zi is the contribution from element i to the total metallicity and the weights count the neutron to proton ratio in the nucleus of this element, i.e.,  where Ni is the neutron number and Ai is the nucleon number of element i. This is implied in the right eq. (6) and used in (7). To be very accurate one should use individual weights for every isotope of element i. We do not take into consideration a possible minute fraction of heavier baryons in very energetic environments. Neither do we count minute fractions of deuterium and helium-3.
where Ni is the neutron number and Ai is the nucleon number of element i. This is implied in the right eq. (6) and used in (7). To be very accurate one should use individual weights for every isotope of element i. We do not take into consideration a possible minute fraction of heavier baryons in very energetic environments. Neither do we count minute fractions of deuterium and helium-3. - 3
Or in correct field units
 , see p. 403 in [43].
, see p. 403 in [43].