The phenomenology of the quantum-corrected gravitational force

Newton's gravitational force has been derived from the Heisenberg uncertainty principle by McCulloch in [1]. The author in [1] has considered a two-body system from the viewpoint of quantum mechanics and found Newtonian gravitational force. In a two-body system, as the distance between the bodies decreases, the position uncertainty decreases. Based on the standard uncertainty principle, their momentum uncertainty and also the force on them increase. Assuming that both bodies are collections of some Planck masses, one can take into account all the possible interactions from the viewpoint of quantum mechanics and derive the Newtonian gravitational force. The gravitational potential energy of a system of two arbitrary objects with mass m is $U=\frac{G m^2}{r}$, where r is the separation between the masses and G is the gravitational constant. One can define the Planck mass as the mass of each object, if U is equal to the energy of a photon whose wavelength is the separation between masses, $\frac{G m_p^2}{r}=\frac{\hbar c}{r}$. 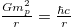Hence, one can conclude that $m_p=\sqrt{\hbar c/G}$. The mass m_p is the maximum mass for which quantum mechanics can be applied.

To obtain the gravitational force, one can consider a mass m which is orbiting the other mass M. It is possible to consider the masses m and M as the collections of Planck masses. Now, one can specify one Planck mass within m and another Planck mass within M and apply the Heisenberg uncertainty principle

$$\begin{equation} \Delta x \Delta p \sim \hbar, \end{equation} \tag{ 1 }$$

where x and p are their mutual position and momentum, respectively. Assuming that $m=nm_p$ and $M=Nm_p$, one can write

$$\begin{equation} \Delta \bar{p} \Delta \bar{x} \sim \sum_{i=1}^N \sum_{j=1}^n \hbar. \end{equation} \tag{ 2 }$$

It is possible to consider the uncertainty of the average position as the separation between two objects in the two-body system. Hence, eq. (2) can be written as

$$\begin{equation} \frac{\Delta \bar{E} \quad r}{c} \sim \sum_{i=1}^N \sum_{j=1}^n \hbar, \end{equation} \tag{ 3 }$$

in which r is the separation between m and M in the mutual orbit and the relation E = pc has been used. Expressing the energy uncertainty as the work done on the system, one can write

$$\begin{equation} \frac{F r^2}{c} \sim \sum_{i=1}^N \sum_{j=1}^n \hbar. \end{equation} \tag{ 4 }$$

Substituting 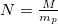$N=\frac{M}{m_p}$ and $n=\frac{m}{m_p}$ in eq. (4), one can find

$$\begin{equation} \frac{F r^2}{c} \sim \frac {mM \hbar}{m_p^2}, \end{equation} \tag{ 5 }$$

which can be rewritten as the Newtonian gravitational force

$$\begin{equation} F \sim \frac {GmM}{r^2}. \end{equation} \tag{ 6 }$$

The gravitational force has been derived from the viewpoint of the Heisenberg uncertainty principle in quantum mechanics [1].

Of course, the Heisenberg uncertainty principle can be replaced by the generalized uncertainty principle (GUP) in quantum field theory. In string theory, it is impossible to find distances shorter than the string length. The existence of such a minimal length on the order of the Planck length necessitates some corrections into the standard uncertainty principle. The generalized uncertainty principle can incorporate the existence of the minimal length [2]. The generalized uncertainty principle is motivated in different approaches. It can be a result of string theory [2–6] or quantum gravitational consideration [7–13]. Among the various versions of the GUP, one can consider

$$\begin{equation} \Delta x=\frac{\hbar}{\Delta p}+ \alpha l_p^2\frac{\Delta p}{\hbar}, \end{equation} \tag{ 7 }$$

where α is considered as a quantity of order one and l_p is the Planck length. It may be interesting to investigate the effects of GUP on the gravitational force.

In this paper, we are going to investigate the effects of the GUP on Newton's gravitational force in high-energy physics. The modified gravitational force is applied to derive the modified Binet's equation. The GUP correction to Binet's equation is functionally the same as the one obtained via general relativity. It seems that the modified Binet's equation within the GUP may provide the precession of the perihelion of Mercury from the viewpoint of quantum mechanics. The modified gravitational force has also been applied to derive the modified Friedmann equation. The GUP correction terms in Friedmann equation may play the role of dark energy to support an accelerating universe within quantum mechanics.

The author in [1] obtained the Newtonian gravitational force by using the Heisenberg uncertainty principle. It may be interesting to study the effects of the generalized uncertainty principle on the gravitational force. Following the quantum mechanical approach proposed by the author in [1], which has been explained in the previous section, we start with the generalized uncertainty principle in (7) to derive the corrections to the gravitational force. Assuming that both masses in the two-body system are composed of Planck masses, one can write

$$\begin{equation} \Delta \bar{p} \Delta \bar{x} \sim \sum_{i=1}^N \sum_{j=1}^n \hbar+\frac{ \alpha l_p^2}{ \hbar }{\Delta \bar{p}^2}, \end{equation} \tag{ 8 }$$

or

$$\begin{equation} \Delta \bar{p} \sim \frac{\Sigma_{i=1}^N \Sigma_{j=1}^n \hbar}{\Delta \bar{x}}+\frac{ \alpha l_p^2}{ \hbar }\frac{\Delta \bar{p}^2}{\Delta \bar{x}}. \end{equation} \tag{ 9 }$$

Up to the first order of α, the square of eq. (9) can be written as

$$\begin{equation} \Delta \bar{p}^2 \sim \left(\frac{\Sigma_{i=1}^N \Sigma_{j=1}^n \hbar}{\Delta \bar{x}}\right)^2+\frac{2 \alpha l_p^2}{ \hbar }\left(\sum_{i=1}^N \sum_{j=1}^n \hbar\right)\frac{\Delta \bar{p}^2}{\Delta \bar{x}^2}. \end{equation} \tag{ 10 }$$

Substituting $\Delta \bar{p}^2$ in eq. (8) yields

$$\begin{equation} \Delta \bar{p} \Delta \bar{x}\sim \sum_{i=1}^N \sum_{j=1}^n \hbar+\frac{\alpha l_p^2}{ \hbar}\frac{(\Sigma_{i=1}^N \Sigma_{j=1}^n \hbar)^2}{\Delta \bar{x}^2}, \end{equation} \tag{ 11 }$$

where the correction terms are written up to the first order of α. In the same manner as in the previous section, we can use 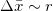$\Delta \bar{x} \sim r$, E = pc and $E=-Fr$, to find

$$\begin{equation} F \sim -\frac{GmM}{r^2}-\frac{\alpha G^3 m^2 M^2}{c^4 r^4}, \end{equation} \tag{ 12 }$$

which is the modified gravitational force in the presence of GUP in the realm of high-energy physics. Here, we have applied $l_p=\sqrt{\frac{G \hbar}{c^3}}$ and $m_p=\sqrt{\frac{c \hbar}{G}}$. The modified gravitational force obtained within the GUP is functionally consistent with the one obtained via other approaches in [14–18]. In the case $\alpha=0$, the modified gravitational force reduces to the Newtonian gravitational force.

Using eq. (12), one can compute $\frac{F}{m}$ as

$$\begin{equation} \frac{F}{m} \sim -\frac{GM}{r^2}-\frac{\alpha G^3 m M^2}{c^4 r^4}. \end{equation} \tag{ 13 }$$

The right-hand side of eq. (13) depends explicitly on the mass of the test body. It shows that the weak equivalence principle can be violated in the presence of the generalized uncertainty principle. The violation of the weak equivalence principle has also been shown in [19–22].

It is now possible to use the modified gravitational force to derive Binet's equation. Following the approach in [23,24], one can derive Binet's equation in the presence of the GUP effects. Using the modified gravitational force in (12), one can write Newton's second law as

$$\begin{equation} m\ddot{r}\hat{r} \sim -\frac{GmM }{r^2}\hat{r}-\frac{\alpha G^3 m^2 M^2 }{c^4r^4}\hat{r}. \end{equation} \tag{ 14 }$$

The angular momentum is 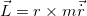$\vec{L}=r \times m \vec{\dot{r}}$. Hence one can deduce that

$$\begin{equation} \frac{\mathrm{d}\vec{L}}{\mathrm{d}t}=0. \end{equation} \tag{ 15 }$$

It means that the angular momentum is conserved as

$$\begin{equation} \vec{L}=m \vec{l}, \end{equation} \tag{ 16 }$$

where $\vec{l}$ is a constant vector. Therefore, one can conclude that the particle is always restricted to move in a plane. In polar coordinates, we have

$$\begin{equation} (\ddot{r}-r\dot{\phi}^2)\hat{r}+\frac{1}{r}\frac{\mathrm{d}}{\mathrm{d}t}(r^2 \dot{\phi})\hat{\phi}=-\frac{ GM}{r^2}\hat{r}-\frac{\alpha G^3 m M^2}{c^4r^4}\hat{r}. \end{equation} \tag{ 17 }$$

Taking the scalar product of eq. (17) with $\hat{\phi}$ and integrating leads to

$$\begin{equation} r^2 \dot{\phi}=l, \end{equation} \tag{ 18 }$$

which emphasizes the conservation of the angular momentum again. Taking the scalar product of eq. (17) with 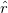$\hat{r}$ leads to

$$\begin{equation} \ddot{r}-r\dot{\phi}^2 =-\frac{GM}{r^2}-\frac{\alpha G^3 m M^2}{c^4r^4}. \end{equation} \tag{ 19 }$$

We are interested in finding the equation of orbits of particle in polar coordinates as 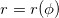$r=r(\phi)$. Introducing $u=\frac{1}{r}$, one can rewrite eq. (19) as

$$\begin{equation} \frac{\mathrm{d}^2u}{\mathrm{d}\phi^2}+u=\frac{GM}{l^{2}}+\frac{\alpha G^3 m M^2}{l^2 c^4 }u^2, \end{equation} \tag{ 20 }$$

which is the modified Binet's equation. In the absence of GUP effects, $\alpha=0$, it can be reduced to

$$\begin{equation} \frac{\mathrm{d}^2u}{\mathrm{d}\phi^2}+u=\frac{GM}{l^2}, \end{equation} \tag{ 21 }$$

which is the classical Binet's equation with the solution

$$\begin{equation} u_0=\frac{GM}{l^2}(1+e \cos \phi). \end{equation} \tag{ 22 }$$

The parameter e is the eccentricity which determines the shape of orbit. In the presence of GUP effects, one can solve the modified Binet's equation in (20) and find

$$\begin{equation} u=\frac{GM}{l^2}\left(1+e \cos \phi+\frac{\epsilon GMe\phi}{l^2} \sin \phi \right)\!, \end{equation} \tag{ 23 }$$

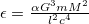where $\epsilon=\frac{\alpha G^3 m M^2}{l^2c^4}$. Some manipulations lead to

$$\begin{equation} u=\frac{GM}{l^2}\left[1+e \cos \left(\phi - \frac{\epsilon GM}{l^2} \phi \right)\right]\!. \end{equation} \tag{ 24 }$$

The orbit of the particle is approximately an ellipse with the period of $2\pi(1+\frac{\epsilon GM}{l^2})$. The precession of the perihelion can be obtained as

$$\begin{equation} \frac{2\pi\epsilon GM}{l^2}=\frac{2 \alpha \pi G^2 mM }{a^2 c^4 (1-e^2)^2}, \end{equation} \tag{ 25 }$$

where a is the semi-major axis of the ellipse. We have applied the GUP in the context of Newtonian mechanics and obtained a modified version of Binet's equation. The modified Binet's equation can explain the precession of the perihelion of planets by choosing the suitable values of α.

On the other hand, Binet's equation has been obtained in the context of general relativity as

$$\begin{equation} \frac{\mathrm{d}^2u}{\mathrm{d}\phi^2}+u=\frac{GM}{l^2}+3{M}u^2. \end{equation} \tag{ 26 }$$

Historically, it has been investigated that Newtonian mechanics is not able to explain the advance of the perihelion of Mercury completely. However, general relativity can successfully provide the residual perihelion precession of Mercury of about 43 seconds of arc per century by the the correction term, 3Mu² in eq. (26). More detailed information is available in [23,24].

Comparing eqs. (20) and (26), one can conclude that the GUP-corrected Binet's equation is functionally the same as the one in general relativity (GR). Choosing the suitable values of α, the GUP effects may provide the residual precession of the perihelion of planets orbiting the Sun in the context of Newtonian mechanics.

It is possible to compare the two formulae for precession, namely

$$\begin{equation} \Delta \phi_{\textit{GUP}} = \frac{2 \alpha \pi G^2 mM }{a^2 c^4 (1-e^2)^2} \end{equation} \tag{ 27 }$$

and

$$\begin{equation} \Delta \phi_{GR} = \frac{6 \pi G M}{ac^2(1-e^2)}. \end{equation} \tag{ 28 }$$

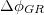Here, $\Delta \phi_{GUP}$ is written from eq. (25) and $\Delta \phi_{GR}$ has been written from [24]. One can find that the GUP can predict the same precession as GR only if 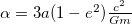$\alpha= 3 a(1-e^2) \frac{c^2}{Gm}$. By some calculations, one can find that the GUP parameter $\alpha \simeq 10^{12}$ can provide the residual perihelion precession of Mercury of about 43 seconds of arc per century. The GUP parameter estimations in various approaches are available in [25,26]. In other words, the GUP-corrected Binet's equation in the flat background may explain the advance of the perihelion of Mercury as well as general relativity. In the case of the GUP, the precession depends also on the mass m of the planet, whereas in GR this does not happen. One may find a clear violation of the equivalence principle in the GUP approach. Moreover, the deformation parameter α of the GUP should be adjusted according to the mass of the specific planet considered, something which is at odds with the universality of the GUP parameter α.

Here, we have utilized McCulloch method to modify the gravitational force via GUP. According to the McCulloch method, gravity should not act on masses smaller than Planck mass. McCulloch derivation seems to work only for masses in the order of the Planck mass or above. Clearly, it is possible to apply the McCulloch method for macroscopic bodies such as Sun and Mercury. However, there exist experiments with neutrons in the Earth's gravitational field. Nesvizhevsky et al. used neutrons to study the gravitational force [27–30]. Of course, it is interesting to reconcile the McCulloc method with neutron experiments in the Earth's gravitational field which can be investigated in future works.

Now, we consider the universe as a compact spatial region V with a compact boundary S. Assuming a(t) as the scale factor, one can write the radius of the universe as 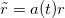$\tilde{r}=a(t)r$. It is necessary to derive the Friedmann equation to describe the dynamics of the universe. Following the manner discussed in [31], the modified gravitational law can lead to the Friedmann equation. One can start with the gravitational force in (12) to find the gravitational potential as

$$\begin{equation} V=-\frac{GmM}{\tilde{r}}-\frac{\alpha G^3 m^2 M^2}{3c^4{\tilde{r}}^3}, \end{equation} \tag{ 29 }$$

where M is the total mass inside the universe and m is the test particle mass near the boundary. The mass inside the volume can be written in terms of the energy density, ${M}=\rho \frac{4}{3} \pi \tilde{r}^3$. Equation (29) can be rewritten as

$$\begin{equation} V=-\frac{4\pi Gm \rho a^2r^2}{3}-\frac{16 \alpha \pi^2 G^3m^2 a^3 r^3 \rho^2}{27c^4}. \end{equation} \tag{ 30 }$$

On the other hand, the kinetic energy is

$$\begin{equation} T=\frac{1}{2}m \dot{\tilde{r}}^2. \end{equation} \tag{ 31 }$$

Hence, one can find the total energy as

$$\begin{equation} U\!=\!\frac{1}{2}m \dot{a}^2r^2\!-\!\frac{4\pi Gm \rho a^2r^2}{3}\!-\!\frac{16 \alpha \pi^2 G^3 m^2 a^3 r^3 \rho^2}{27c^4}. \end{equation} \tag{ 32 }$$

Multiplying both sides of eq. (32) by $\frac{2}{ma^2r^2}$ and rearranging the terms leads to

$$\begin{equation} \left(\frac{\dot{a}}{a}\right)^2=\frac{8 \pi G \rho}{3c^2}-\frac{kc^2}{a^2}+\frac{32\alpha \pi^2 G^3 m \tilde{r} \rho^2}{27 c^4}, \end{equation} \tag{ 33 }$$

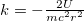where $k=-\frac{2U}{mc^2r^2}$. In the absence of GUP effects, eq. (33) reduces to

$$\begin{equation} \left(\frac{\dot{a}}{a}\right)^2=\frac{8 \pi G \rho}{3c^2}-\frac{kc^2}{a^2}, \end{equation} \tag{ 34 }$$

which has been obtained in [31]. According to eq. (34), k must be independent of r to maintain the homogeneity of the universe. It necessitates that $U \propto r^2$. Moreover, k is independent of time since U is conserved. It seems that k must be considered as a constant. It is interesting to point out that eq. (34) can be precisely the Friedmann equation while k is interpreted as a curvature constant.

By introducing the Hubble parameter, $H=\frac{\dot{a}}{a}$, one can rewrite eq. (33) as

$$\begin{equation} H^2=\frac{8 \pi G \rho}{3c^2}-\frac{kc^2}{a^2}+\frac{32\alpha \pi^2 G^3 m \tilde{r} \rho^2}{27 c^4}, \end{equation} \tag{ 35 }$$

which is the modified Friedmann equation in the presence of GUP effects.

In the case k = 0, one can call the energy density as the critical energy density, which can be written as

$$\begin{equation} \rho_{c}=\frac{3H^2c^2}{8 \pi G}-\frac{\alpha m c^2 \tilde{r} H^4}{16 \pi}. \end{equation} \tag{ 36 }$$

Multiplying $\frac{1}{H^2}$ on both sides of eq. (35) yields

$$\begin{equation} 1=\frac{\rho}{\rho_c}-\frac{kc^2}{a^2H^2}-\frac{ \alpha m c^2 \tilde{r}H^4 \rho}{16 \pi \rho_c^2}+\frac{ 4\alpha \pi G^2 m \tilde{r} \rho^2 }{9 c^2 \rho_c}, \end{equation} \tag{ 37 }$$

in which we have used eq. (36) and applied the Taylor expansion up to the first order of α. It is now convenient to introduce the definitions

$$\begin{eqnarray} \Omega&= \frac{\rho}{\rho_c}, \qquad \Omega_k=-\frac{kc^2}{a^2H^2},\nonumber\\ \Omega_{GUP}&= -\frac{ \alpha m c^2 \tilde{r}H^4 \rho}{16 \pi \rho_c^2}+\frac{ 4\alpha \pi G^2 m \tilde{r} \rho^2} {9 c^2 \rho_c}. \end{eqnarray} \tag{ 38 }$$

As a result, one can write

$$\begin{equation} 1=\Omega+\Omega_k+\Omega_{GUP}. \end{equation} \tag{ 39 }$$

It seems that the GUP correction terms can play the role of a new mysterious energy which is important in studying the universe dynamics. In other words, the GUP correction terms may play role of a dark energy component to provide the universe expansion.

One can study the gravitational force from the viewpoint of quantum mechanics. Some authors have shown that the Newtonian gravitational force can be obtained via the Heisenberg uncertainty principle. However, the Heisenberg uncertainty principle is replaced by the generalized uncertainty principle to support the existence of the minimal observable length in the realm of high-energy physics. We have modified the gravitational force by using the generalized uncertainty principle. Of course, the corrections to the gravitational force may lead to the important results in the gravitational systems. We have applied the modified gravitational force to investigate the corrections into Binet's equation. It is shown that the modified Binet's equation, which is obtained in the presence of GUP effects in the context of Newtonian mechanics, is functionally consistent with the one obtained in general relativity. In other words, the GUP correction term in Binet's equation is functionally the same as the one obtained in general relativity. Using the astrophysical data about the precession of the perihelion of the planets in the Solar System, one can put some constraints on the GUP parameter, α. It is shown that the residual perihelion precession of Mercury can be obtained by choosing the GUP parameter 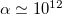$\alpha \simeq 10^{12}$. It is also possible to utilize the modified gravitational force to modify the Friedmann equation in the FRW universe. It seems that the GUP corrections may play the role of dark energy to provide an accelerating universe. As a suggestion, it is interesting to point out that considering the charged masses in the two-body system in the presence of GUP effects leads to the modified Newton-Coulomb's law, which can be investigated in future works.

We thank the referee for comments that greatly improved the manuscript. We are also grateful to Prof. Kourosh Nozari for the useful discussions on an earlier version of the manuscript.