Abstract
The quadrupole topological insulator, which supports robust corner states, has been recently demonstrated in two-dimensional (2D) spatial lattices. Here, we design the first photonic quadrupole topological insulator in fully synthetic spaces with the utilization of 0D optical cavity. The frequency and orbital angular momentum (OAM) of light are used to form the 2D synthetic spaces. Four degenerate polarization states are mapped to the internal lattice sites within the unit cell. By suitably engineering the coupling between cavity modes with different frequencies, OAMs and polarizations, the ideal synthetic quadrupole topological insulator is obtained. By using the robust synthetic corner states, we present the possibility for the realization of topological transportation of multi-photon entangled states. Our designed synthetic photonic quadrupole insulator proposes a unique platform to investigate higher-order topological phases in lower-dimensional systems and possesses potential applications in quantum information and optical communication.
Export citation and abstract BibTeX RIS
Introduction
The exploration of topological physics in both solid materials [1,2] and classical waves systems [3,4] has become one of the most fascinating frontiers in recent years. Based on the bulk-boundary correspondence principle, most of the D-dimensional topological systems studied so far are always featured by the (D−1)-dimensional boundary state [5–14]. Recently, a new class of symmetry-protected higher-order topological insulators that possess robust lower-dimensional boundary states and obey a generalization of the standard bulk-boundary correspondence have been introduced [15–31]. One example is given by the quadrupole topological insulator, which can exhibit (D−2)-dimensional topological states protected by the quantized bulk quadrupole polarization. Motivated by this novel property, many experimental implementations of the 2D quadrupole topological phase with 0D corner states have been realized in microwave [28], phononic [29], photonic [30] and electrical circuit systems [31].
On the other hand, except for the real physical dimensions, various degrees of freedom in photonic systems, such as frequency [32–35], OAM [36–37] and external structural parameters [38–41], are also able to be used to construct the synthetic space where the innovative light control and quantum information processing may be realized. Based on the synthetic dimension in photonics, we can easily investigate higher-dimensional physics with lower-dimensional structures. For example, the Bloch oscillation in synthetic space along the frequency axis has been realized using a single dynamically modulated ring resonator [42]. The effective magnetic field for photons in the 2D synthetic space is achieved in one optical cavity, where the topologically protected one-way edge state along the OAM axis or frequency axis appears [43]. In addition, the 3D topological phases, such as Weyl point and topological insulators, can be constructed using 2D systems with an auxiliary synthetic dimension [44–46]. Furthermore, some novel topological phenomena beyond 3D, such as 4D quantum Hall effects, can also be implemented with the help of synthetic dimensions [40]. In all existing works, only first-order topological phases have been investigated in the synthetic space. The scheme for marrying higher-order topological physics with synthetic spaces, which can find wide applications in robust manipulation of various degrees of freedom in photonics, has never been proposed.
In this work, we design a photonic quadrupole topological insulator in synthetic 2D spaces with the utilization of dynamically modulated 0D optical cavity. The frequency and OAM of light are used to form the 2D synthetic spaces. Four polarization states are mapped to internal lattice sites within the unit cell. By using this synthetic corner state, we prove that the topological transportation of multi-photon entangled states may be achieved. Our work presents a new way to investigate higher-order topological phases in lower-dimensional systems and possesses potential applications in quantum information and optical communications.
Results and discussion
Design of photonic quadrupole topological insulator with synthetic dimensions
We consider the first theoretical model (Benalcazar-Bernevig-Hughes model) for the realization of quadrupole insulators, where the unit cell of its tight-binding lattice model is shown in fig. 1(a). Owing to the fact that quantized quadrupole moment is protected by a pair of anti-commute reflection symmetries along the x and y axes [15], one of the periodic intra-cell/inter-cell (black/yellow lines) couplings should be negative to introduce a gauge flux  per unit cell. In this case, the main challenge to construct the photonic quadrupole insulator is to realize simultaneously both the negative and positive couplings. Here, we show that the quadrupole insulator can be fulfilled in the synthetic space using 0D optical cavity.
per unit cell. In this case, the main challenge to construct the photonic quadrupole insulator is to realize simultaneously both the negative and positive couplings. Here, we show that the quadrupole insulator can be fulfilled in the synthetic space using 0D optical cavity.
Fig. 1: Design of synthetic quadrupole topological insulator in zero-dimensional cavity. (a) The unit cell of the quadrupole insulator. The black/yellow lines correspond to the intra-cell/inter-cell couplings. Here, tx/ty (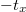 /
/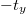 ) correspond to the positive (negative) intra-cell/inter-cell couplings. (b) The lattice model of quadrupole topological phases in synthetic 2D spaces. The frequency and OAM of light are set as two axes in synthetic spaces. Four polarization states
) correspond to the positive (negative) intra-cell/inter-cell couplings. (b) The lattice model of quadrupole topological phases in synthetic 2D spaces. The frequency and OAM of light are set as two axes in synthetic spaces. Four polarization states 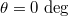 (H), 45 deg (D), 90 deg (V) and 135 deg (
(H), 45 deg (D), 90 deg (V) and 135 deg (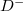 ) are considered as the internal lattice sites within the unit cell. The red and black dot boxes marked the intra- and inter-cell coupling conditions. (c) The designed 0D optical cavities, which include three cavities (polarization, OAM and frequency cavities), can realize the quadrupole topological insulator in synthetic spaces. EOM is the electro-optic phase modulator, SLM is the spatial light modulator, and BS is the beam splitter.
) are considered as the internal lattice sites within the unit cell. The red and black dot boxes marked the intra- and inter-cell coupling conditions. (c) The designed 0D optical cavities, which include three cavities (polarization, OAM and frequency cavities), can realize the quadrupole topological insulator in synthetic spaces. EOM is the electro-optic phase modulator, SLM is the spatial light modulator, and BS is the beam splitter.
Download figure:
Standard imageTo design the synthetic quadrupole topological insulators, it is important to map different degrees of freedom in photonic systems to the real-space tight-binding lattice model with quantized bulk quadrupole polarization. The general conceptual drawing is graphically shown in fig. 1(b). Here, the frequency and OAM of light are set as two axes in synthetic spaces. Four linked polarization modes with the same frequency and OAM are mapped to the intra-cell coupling condition (enclosed by the red dotted box). Four polarization angles used here are set as 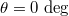 (H-polarized state, purple site), 45 deg (D-polarized state, orange site), 90 deg (V-polarized state, red site) and 135 deg (
(H-polarized state, purple site), 45 deg (D-polarized state, orange site), 90 deg (V-polarized state, red site) and 135 deg (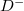 -polarized state, green site), respectively. Additionally, the connection between lattice sites with different frequencies (or OAMs) represents the inter-cell couplings (enclosed by the black dotted box). By suitably designing the coupling strength between optical states with different frequencies, OAMs and polarizations, the ideal quadrupole topological insulators in the synthetic space can be obtained. It is worthy to note that the orthogonality of four polarized states is not the necessary requirement for the realization of required optical mode conversions. The critical point of using four polarization states to map on four lattice sites is to suitably control their modal conversion, where the coupling is only allowed between the sites from the set [H(
-polarized state, green site), respectively. Additionally, the connection between lattice sites with different frequencies (or OAMs) represents the inter-cell couplings (enclosed by the black dotted box). By suitably designing the coupling strength between optical states with different frequencies, OAMs and polarizations, the ideal quadrupole topological insulators in the synthetic space can be obtained. It is worthy to note that the orthogonality of four polarized states is not the necessary requirement for the realization of required optical mode conversions. The critical point of using four polarization states to map on four lattice sites is to suitably control their modal conversion, where the coupling is only allowed between the sites from the set [H(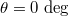 ), V(
), V(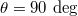 )] and the set [
)] and the set [ ),
), 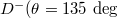 )] but not between the sites in the same set. This can be realized with the cooperation of polarization selection and rotation operations.
)] but not between the sites in the same set. This can be realized with the cooperation of polarization selection and rotation operations.
In the following, we prove that the above-proposed scheme can be realized with the utilization of 0D optical ring cavity in free spaces. Here, the designed optical cavity should support a set of equally spaced resonant modes 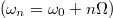 when the dispersion effect is ignored.
when the dispersion effect is ignored. 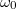 is the frequency of the 0-th mode.
is the frequency of the 0-th mode. 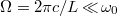 is the free-spectral range of the optical cavity with the loop length being L. n is an integer marking the mode index in the frequency axis. In addition, all optical elements in the cavity are chosen to have cylindrical symmetry, where the degenerated Laguerre-Gaussian modes with different radial (p) and azimuthal (l) indexes exist [43]. Moreover, each cavity mode with fixed OAM and frequency should possess four polarization states (
is the free-spectral range of the optical cavity with the loop length being L. n is an integer marking the mode index in the frequency axis. In addition, all optical elements in the cavity are chosen to have cylindrical symmetry, where the degenerated Laguerre-Gaussian modes with different radial (p) and azimuthal (l) indexes exist [43]. Moreover, each cavity mode with fixed OAM and frequency should possess four polarization states (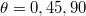 and 135 deg). Hence, the electric field E in this optical cavity can be expanded as
and 135 deg). Hence, the electric field E in this optical cavity can be expanded as

where 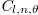 is the amplitude for the cavity mode at frequency
is the amplitude for the cavity mode at frequency 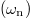 , OAM (l) and polarization
, OAM (l) and polarization 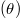 .
. 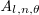 (r) is the corresponding modal profile perpendicular to the direction of beam propagation.
(r) is the corresponding modal profile perpendicular to the direction of beam propagation. 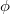 denotes the azimuthal coordinate. These different cavity modes (
denotes the azimuthal coordinate. These different cavity modes (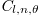 ) can be mapped to the synthetic lattice sites in fig. 1(a). In this case, the synthetic quadrupole topological insulator can be created by suitably engineering the coupling strength between these cavity modes. To fulfill the ideal coupling configuration, the large optical cavity consisting of three parts (polarization cavity, OAM cavity and frequency cavity) is designed, as shown in fig. 1(c).
) can be mapped to the synthetic lattice sites in fig. 1(a). In this case, the synthetic quadrupole topological insulator can be created by suitably engineering the coupling strength between these cavity modes. To fulfill the ideal coupling configuration, the large optical cavity consisting of three parts (polarization cavity, OAM cavity and frequency cavity) is designed, as shown in fig. 1(c).
The intra-cell coupling within the synthetic lattice model can be achieved by using the designed polarization cavity (enclosed by the red dot box), where the required polarization conversions at the fixed frequency and OAM can be realized. In the synthetic unit cell, the coupling is allowed between the sites from the set {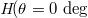 ),
), 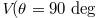 )}and the set {
)}and the set {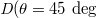 ),
), 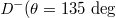 )}but not between the sites in the same set. In this case, only eight kinds of polarization coupling
)}but not between the sites in the same set. In this case, only eight kinds of polarization coupling 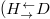 ,
, 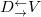 ,
,  and
and 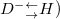 are allowed. Coupling here means polarization inter-conversion. To fulfill this requirement, eight sub-loops with the same length L (coupling phase being
are allowed. Coupling here means polarization inter-conversion. To fulfill this requirement, eight sub-loops with the same length L (coupling phase being 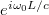 ) are designed. Each loop contains a polarization selector (only specific polarization state can pass through marked by colored triangles) and a polarization rotator (
) are designed. Each loop contains a polarization selector (only specific polarization state can pass through marked by colored triangles) and a polarization rotator (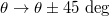 shown by colored squares). In this case, when the H-polarized cavity mode enters in the polarization cavity, it can only go through the purple polarization selector. Then, the H-polarized mode is converted to D (and
shown by colored squares). In this case, when the H-polarized cavity mode enters in the polarization cavity, it can only go through the purple polarization selector. Then, the H-polarized mode is converted to D (and 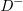 )-polarized modes based on the polarization rotator, where the polarization angle is increased (decreased) by 45 deg. After these two steps, the modal coupling of
)-polarized modes based on the polarization rotator, where the polarization angle is increased (decreased) by 45 deg. After these two steps, the modal coupling of 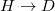 and
and 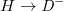 can be realized. Similarly, other sub-loops with different polarization selection and rotation operations are used to realize polarization inter-conversion with entered polarization states being D, V and
can be realized. Similarly, other sub-loops with different polarization selection and rotation operations are used to realize polarization inter-conversion with entered polarization states being D, V and 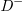 , respectively. Remarkably, like the quadrupole insulator in real space, the negative intra-cell coupling should also be introduced in the synthetic space when the polarization inter-conversion of
, respectively. Remarkably, like the quadrupole insulator in real space, the negative intra-cell coupling should also be introduced in the synthetic space when the polarization inter-conversion of 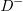 and H is carried out. This can be easily achieved by using a phase retarder (marked by yellow rectangles in fig. 1(b)) with a
and H is carried out. This can be easily achieved by using a phase retarder (marked by yellow rectangles in fig. 1(b)) with a 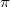 phase delay. Moreover, the reflectivity of different beam splitters (BSs) used here should be suitably engineered to make the absolute value of the intra-cell coupling coefficients become identical. Here,
phase delay. Moreover, the reflectivity of different beam splitters (BSs) used here should be suitably engineered to make the absolute value of the intra-cell coupling coefficients become identical. Here, 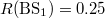 ,
, 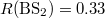 and
and 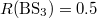 .
.
Based on the coupled mode theory, the change of the modal amplitude after each round trip within the polarization cavity can be expressed as (the coupling phase 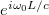 is a global phase, which can be neglected without loss of generality):
is a global phase, which can be neglected without loss of generality):

where the value of coupling coefficient is expressed as 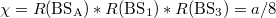 (a is the reflectivity of the "
(a is the reflectivity of the "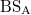 "). It is clearly shown that our designed modal conversion configuration induced by the polarization cavity possesses an ideal correspondence to the intra-cell coupling of the lattice model with quantized bulk quadrupole polarization.
"). It is clearly shown that our designed modal conversion configuration induced by the polarization cavity possesses an ideal correspondence to the intra-cell coupling of the lattice model with quantized bulk quadrupole polarization.
On the other hand, to introduce appropriate inter-cell couplings between different synthetic unit cells, another two cavities (enclosed by black dot boxes in fig. 1(b)) with either OAM or frequency control should be designed. Firstly, we focus on the modal coupling with different OAMs and polarizations (but the same frequency) by using an OAM modulated cavity with four sub-loops. Here, only four kinds of modal couplings, that are  ,
, 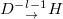 ,
, 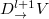 and
and 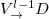 , are allowed. The length of each loop is equal to L so that the global coupling phase
, are allowed. The length of each loop is equal to L so that the global coupling phase 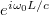 can be neglected. To fulfill the coupling between cavity modes with different OAMs, each sub-loop should possess a spatial light modulator (SLM) to change the OAM of light by either +1 or −1. In addition, each sub-loop should also possess required polarization control to achieve the accompanied polarization conversions. For cases of
can be neglected. To fulfill the coupling between cavity modes with different OAMs, each sub-loop should possess a spatial light modulator (SLM) to change the OAM of light by either +1 or −1. In addition, each sub-loop should also possess required polarization control to achieve the accompanied polarization conversions. For cases of 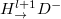 and
and 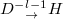 , a
, a 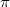 phase delay is applied to introduce the negative inter-cell couplings. In this condition, when the V-polarized fields enter in the OAM cavity, it can only pass through the red polarization selector. Then, the designed polarization rotator converts the V-polarized mode to the D-polarized mode. Finally, the OAM index of the D-polarized cavity mode decreases by one with the help of the SLM. Based on these three steps, the modal coupling of
phase delay is applied to introduce the negative inter-cell couplings. In this condition, when the V-polarized fields enter in the OAM cavity, it can only pass through the red polarization selector. Then, the designed polarization rotator converts the V-polarized mode to the D-polarized mode. Finally, the OAM index of the D-polarized cavity mode decreases by one with the help of the SLM. Based on these three steps, the modal coupling of 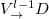 can be realized. Similarly, other sub-loops are used to realize modal conversion with entered polarization states being H, D and
can be realized. Similarly, other sub-loops are used to realize modal conversion with entered polarization states being H, D and 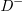 , respectively.
, respectively.
Based on the above discussion, the variation of cavity modes with the light travelling a round trip within the OAM cavity can be expressed as

where the coupling coefficient can be expressed as ![${\kappa}=[1-R({\text{BS}}_{\mathrm{A}})]*R({\text{BS}}_{\mathrm{B}})*R({\text{BS}}_{1})=(1-{a})b/4$](https://content.cld.iop.org/journals/0295-5075/131/2/24004/revision1/epl20222ieqn54.gif) (b is the reflectivity of "
(b is the reflectivity of "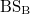 ").
").
Except for the modal coupling with different OAMs, the conversion between cavity modes with different frequencies and polarizations (but the same OAM) should also be achieved. Here, four kinds of modal couplings, that are 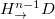 ,
, 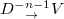 ,
, 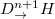 and
and 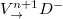 , are allowed. The length of each sub-loop in the frequency cavity is L. To realize modal coupling with different frequency, each sub-loop possesses an electro-optic phase modulators (EOMs) to induce time-dependent transmissions [42–44]. There are two different transmission coefficients induced by EOMs, which can be expressed as
, are allowed. The length of each sub-loop in the frequency cavity is L. To realize modal coupling with different frequency, each sub-loop possesses an electro-optic phase modulators (EOMs) to induce time-dependent transmissions [42–44]. There are two different transmission coefficients induced by EOMs, which can be expressed as ![$T=e^{i\beta [\cos (\Omega_{M}t)\pm i\sin({\Omega_{M}}t)]}$](https://content.cld.iop.org/journals/0295-5075/131/2/24004/revision1/epl20222ieqn60.gif) , where
, where 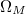 is the modulation frequency and
is the modulation frequency and 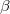 denotes the modulation amplitude. In the presence of a travelling signal
denotes the modulation amplitude. In the presence of a travelling signal 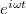 , the transmitted wave can be expressed as
, the transmitted wave can be expressed as 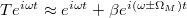 . It is clearly shown that the proposed EOM can change the modal frequency by either
. It is clearly shown that the proposed EOM can change the modal frequency by either 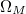 or
or 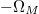 . Combining this dynamically modal control and suitable polarization manipulations, the ideal inter-cell coupling along frequency dimension can be realized. For example, the
. Combining this dynamically modal control and suitable polarization manipulations, the ideal inter-cell coupling along frequency dimension can be realized. For example, the  -polarized fields entering in the frequency cavity can only pass through the green polarization selector. Then, the designed polarization rotator can convert the
-polarized fields entering in the frequency cavity can only pass through the green polarization selector. Then, the designed polarization rotator can convert the 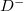 -polarized mode to the V-polarized mode. Finally, based on the dynamically modulated EOM, the frequency index of the V-polarized cavity mode changes to
-polarized mode to the V-polarized mode. Finally, based on the dynamically modulated EOM, the frequency index of the V-polarized cavity mode changes to 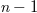 . In this case, the modal coupling of
. In this case, the modal coupling of 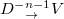 is fulfilled.
is fulfilled.
In the weak modulation regime and without the detuning of the modulation frequency from the free-spectral range of the cavity 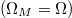 , the change of the modal amplitude after each round trip with light passing through the EOM gives:
, the change of the modal amplitude after each round trip with light passing through the EOM gives:

Here, the coupling coefficient should be expressed as ![$g={\beta}[1-R({\text{BS}}_{\mathrm{A}})]*[1-R({\text{BS}}_{\mathrm{B}})]*R({\text{BS}}_{1})= {\beta}(1-\textit{a})(1-b)/4$](https://content.cld.iop.org/journals/0295-5075/131/2/24004/revision1/epl20222ieqn72.gif) .
.
Combing the modal coupling equations (eqs. (2)–(4)), the Hamiltonian of such an optical cavity can be expressed as
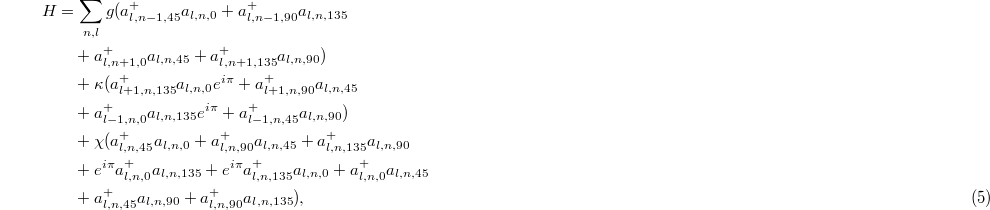
where we set 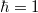 .
. 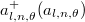 is the creation (annihilation) operator for the cavity mode with frequency n, OAM l and polarization
is the creation (annihilation) operator for the cavity mode with frequency n, OAM l and polarization  . We note that the diagonal terms are zero since each cavity mode is completely converted to other nearest-neighbor coupled modes when it travels a round trip within the cavity. The Hamiltonian in eq. (4) presents the same form with that of the quadrupole topological insulator in real space [24,25]. In following parts, we assume that inter-cell couplings along frequency and OAM axes are identical
. We note that the diagonal terms are zero since each cavity mode is completely converted to other nearest-neighbor coupled modes when it travels a round trip within the cavity. The Hamiltonian in eq. (4) presents the same form with that of the quadrupole topological insulator in real space [24,25]. In following parts, we assume that inter-cell couplings along frequency and OAM axes are identical 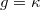 . This can be realized when the modulation strength and reflectivity of "
. This can be realized when the modulation strength and reflectivity of " " satisfy
" satisfy  ). Additionally, a recent experiment demonstrates that the value of
). Additionally, a recent experiment demonstrates that the value of 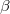 can be set around 0.3 [47]. In this case, the reflectivity of "
can be set around 0.3 [47]. In this case, the reflectivity of " " is about
" is about 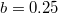 and the ratio between the intra-cell and inter-cell coupling should be expressed as
and the ratio between the intra-cell and inter-cell coupling should be expressed as 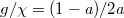 . Hence, we can easily tune the topological gap size by changing the reflectivity of
. Hence, we can easily tune the topological gap size by changing the reflectivity of  with fixed value of
with fixed value of 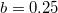 and
and 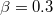 . In the following numerical calculations, we always set
. In the following numerical calculations, we always set 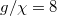 (
(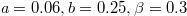 ),
), 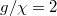 (
(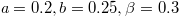 ) and
) and 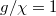 (
(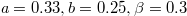 ), which are realizable in terms of state-of-the-art experiments, for most results.
), which are realizable in terms of state-of-the-art experiments, for most results.
To exhibit the higher-order topological effect in our designed synthetic space, the artificial boundaries along both frequency and OAM axes should be included. This is not a trivial problem since the boundaries are not real. We can follow the previous work to introduce the frequency boundary [43] by coupling with a secondary cavity, which is designed to be resonant with the frequency 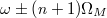 , but to be off-resonant with other modes in the range [
, but to be off-resonant with other modes in the range [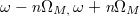 ]. Such a secondary cavity can construct artificial boundaries at
]. Such a secondary cavity can construct artificial boundaries at 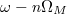 and
and 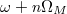 . It is also worthy to note that the coupling coefficient between the main and second cavity should be sufficiently large at the resonance frequency to create an ideal frequency boundary [43]. In addition, to create the edge in the OAM space, the
. It is also worthy to note that the coupling coefficient between the main and second cavity should be sufficiently large at the resonance frequency to create an ideal frequency boundary [43]. In addition, to create the edge in the OAM space, the  (
(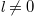 ) mode should leaky out from (propagate in) the cavity. In this case, the key of creating the OAM boundary is the design of holes in BSs, which should let the mode with
) mode should leaky out from (propagate in) the cavity. In this case, the key of creating the OAM boundary is the design of holes in BSs, which should let the mode with 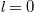 pass through with high probability and not significantly affect the
pass through with high probability and not significantly affect the 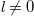 modes [37]. Actually, there are many factors limiting the size of the synthetic lattice, for example, the effective operation range of the optical elements. Here, we assume that frequency boundaries locate at
modes [37]. Actually, there are many factors limiting the size of the synthetic lattice, for example, the effective operation range of the optical elements. Here, we assume that frequency boundaries locate at 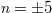 and OAM boundaries are chosen as
and OAM boundaries are chosen as  and
and  . In this case, the finite lattice model with open boundary condition is generated in the synthetic space where totally 484 sites (11 resonant frequencies, 11 OAMs and 4 polarizations) exist in this system. To illustrate the relationship between the topological property and the ratio between inter- and intra-cell coupling in synthetic dimensions, we plot the evolution of eigen-spectrum of Hamiltonian (eq. (5)) with different values of
. In this case, the finite lattice model with open boundary condition is generated in the synthetic space where totally 484 sites (11 resonant frequencies, 11 OAMs and 4 polarizations) exist in this system. To illustrate the relationship between the topological property and the ratio between inter- and intra-cell coupling in synthetic dimensions, we plot the evolution of eigen-spectrum of Hamiltonian (eq. (5)) with different values of 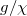 (
(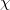 is normalized to be 1), as shown in fig. 2(a). For the practical realization of these different coupling relations, the reflectivity of "
is normalized to be 1), as shown in fig. 2(a). For the practical realization of these different coupling relations, the reflectivity of " " should be suitably adjusted with fixed values of b and
" should be suitably adjusted with fixed values of b and 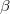 . We find that there is neither edge nor corner state within the trivial bulk band gap when
. We find that there is neither edge nor corner state within the trivial bulk band gap when 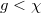 (
(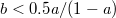 ). And, the topological phase transition appears at the point with
). And, the topological phase transition appears at the point with 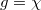 where the bulk band gap gets closed. Beyond the transition point (
where the bulk band gap gets closed. Beyond the transition point (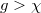 ), the bulk gap opens again. Then, both edge and midgap corner states appear. This can be further shown in fig. 2(b) where the corresponding eigenvalues at g = 8 (
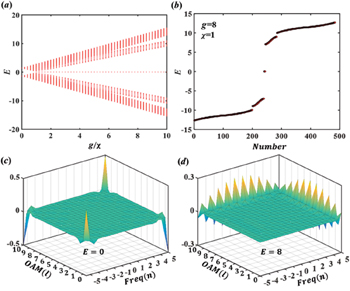
), the bulk gap opens again. Then, both edge and midgap corner states appear. This can be further shown in fig. 2(b) where the corresponding eigenvalues at g = 8 (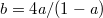 ) are plotted. It is found that both fourfold degenerate "zero-energy" corner states and gapped edge states exist in this topologically non-trivial band gap. To clearly illustrate the midgap corner and edge states, in figs. 2(c) and (d), the distribution of the corner (E = 0) and edge (E = 8) states in the synthetic space are plotted. As expected, the eigenmode is highly localized at corners or edges within the finite lattice model in synthetic spaces that is the same as the quadrupole topological insular in real spaces.
) are plotted. It is found that both fourfold degenerate "zero-energy" corner states and gapped edge states exist in this topologically non-trivial band gap. To clearly illustrate the midgap corner and edge states, in figs. 2(c) and (d), the distribution of the corner (E = 0) and edge (E = 8) states in the synthetic space are plotted. As expected, the eigenmode is highly localized at corners or edges within the finite lattice model in synthetic spaces that is the same as the quadrupole topological insular in real spaces.
Fig. 2: Eigenspectrum and eigenmodes for the synthetic quadrupole topological insulator. (a) The evolution of eigenspectrum with different values of 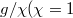 ). (b) The eigenspectrum at g = 8. (c) and (d): the modal distribution of corner and edge states in the synthetic space.
). (b) The eigenspectrum at g = 8. (c) and (d): the modal distribution of corner and edge states in the synthetic space.
Download figure:
Standard imageTopologically protected evolution of corner state in synthetic spaces
To characterize the evolution of corner and edge states in the synthetic space, we perform numerical simulation of output fields from the designed optical cavity. The general coupled-mode equations for our designed synthetic quadrupole topological insulators with the consideration of input and output ports can be expressed as
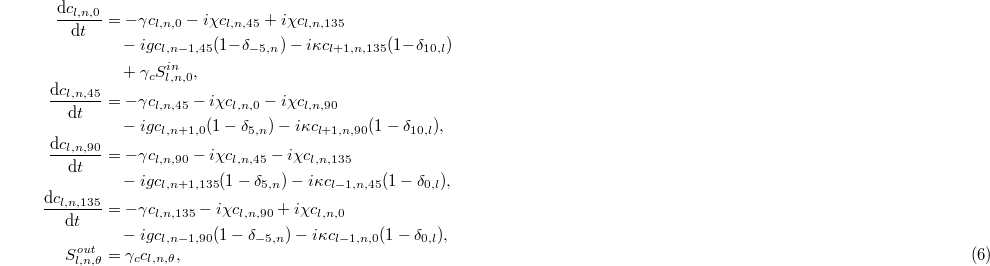
where 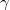 is the total lossy rate of each cavity mode and
is the total lossy rate of each cavity mode and 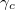 is the decay rate through the coupling between the optical cavity and the input-output channel. We assume that all cavity modes couple to the input-output channel with equal rates.
is the decay rate through the coupling between the optical cavity and the input-output channel. We assume that all cavity modes couple to the input-output channel with equal rates. 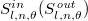 is the input (output) modal amplitude at frequency n, OAM l and polarization
is the input (output) modal amplitude at frequency n, OAM l and polarization  . The artificial boundary in the synthetic space is chosen as
. The artificial boundary in the synthetic space is chosen as 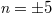 ,
, 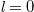 and
and 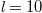 . Here, we only focus on the case that the polarization angle of input signal is 0 deg. The results with other input polarizations are identical.
. Here, we only focus on the case that the polarization angle of input signal is 0 deg. The results with other input polarizations are identical.
In our simulations, we set the total lossy rate of each cavity mode as 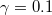 and the coupling rate between the input (and output) port and the optical cavity as
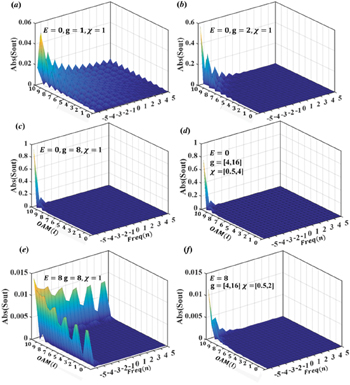
and the coupling rate between the input (and output) port and the optical cavity as 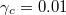 . And, all other parameters are identical with those used in the calculation of eigen spectrum shown in fig. 2(a). To effectively excite the synthetic corner state, the input signal should locate at the corner (left-up) of the synthetic space. No corner excitation appears when the input state locates in the bulk of the synthetic space. Figures 3(a)–(c) show the steady-state modal distribution with the value of
. And, all other parameters are identical with those used in the calculation of eigen spectrum shown in fig. 2(a). To effectively excite the synthetic corner state, the input signal should locate at the corner (left-up) of the synthetic space. No corner excitation appears when the input state locates in the bulk of the synthetic space. Figures 3(a)–(c) show the steady-state modal distribution with the value of 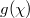 being 1(1), 2(1) and 8(1), respectively. The input signal is selected as
being 1(1), 2(1) and 8(1), respectively. The input signal is selected as 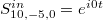 ("zero energy" excitation). We find that no corner localization appears when the coupling strength satisfied the relationship of
("zero energy" excitation). We find that no corner localization appears when the coupling strength satisfied the relationship of 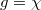 . This is because no band gap exists in this case. While, with increasing the value of
. This is because no band gap exists in this case. While, with increasing the value of 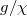 , the concentration of the output optical mode at the corner of the synthetic space appears. Additionally, the modal profile is completely the same as the midgap corner state, as shown in fig. 2(c). Moreover, the larger the value of g/
, the concentration of the output optical mode at the corner of the synthetic space appears. Additionally, the modal profile is completely the same as the midgap corner state, as shown in fig. 2(c). Moreover, the larger the value of g/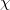 is, the more significant localization appears at the corner of the synthetic space. Except for the corner excitation, the synthetic edge state can also be excited with the input signal being
is, the more significant localization appears at the corner of the synthetic space. Except for the corner excitation, the synthetic edge state can also be excited with the input signal being 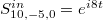 , as shown in fig. 3(e).
, as shown in fig. 3(e).
Fig. 3: Evolution of corner and edge states in synthetic spaces. (a)–(c) The steady-state modal distribution of corner state with the value of  being 1(1), 2(1) and 8(1), respectively. (d) The steady-state modal distribution of corner state under the influence of disorder where
being 1(1), 2(1) and 8(1), respectively. (d) The steady-state modal distribution of corner state under the influence of disorder where 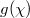 are randomly selected ranging from 4(0.5) to 16(4) between different lattice sites. (e) The steady-state modal distribution of edge state with the value of
are randomly selected ranging from 4(0.5) to 16(4) between different lattice sites. (e) The steady-state modal distribution of edge state with the value of 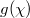 being 1(8). (f) The steady-state modal distribution of edge state under the influence of disorder where g
being 1(8). (f) The steady-state modal distribution of edge state under the influence of disorder where g is randomly selected ranging from 4(0.5) to 16(4).
is randomly selected ranging from 4(0.5) to 16(4).
Download figure:
Standard imageThe most important property of the topologically protected corner state is that it is robust with disorders. To illustrate this phenomenon, we calculate the steady-state solution of the output field with significant disorders on g/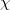 at different lattice sites. The configuration average (50 times) is performed to eliminate the accidental result in the disorder system. The results are shown in fig. 3(d). We find that sharply localized output fields at the corner of the synthetic space still exist at zero energy when the values of
at different lattice sites. The configuration average (50 times) is performed to eliminate the accidental result in the disorder system. The results are shown in fig. 3(d). We find that sharply localized output fields at the corner of the synthetic space still exist at zero energy when the values of 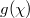 on different lattice sites are randomly selected ranging from 4(0.5) to 16(4). It clearly reveals the robustness of the corner state for the synthetic quadrupole topological insulator. On contrary to the corner state, the excited edge state is significantly disturbed by the disorder in the bulk, as shown in fig. 3(f).
on different lattice sites are randomly selected ranging from 4(0.5) to 16(4). It clearly reveals the robustness of the corner state for the synthetic quadrupole topological insulator. On contrary to the corner state, the excited edge state is significantly disturbed by the disorder in the bulk, as shown in fig. 3(f).
The topologically protected transportation of multi-photon entangled states in the optical cavity with synthetic corner states
A fascinating potential application of our designed synthetic quadrupole topological insulator is the realization of topologically protected transportation of multi-photon entangled states. Creation and transportation of entangled optical states have been extensively investigated in recent years. However, many errors arising from random disorders limit their efficiencies. The discoveries regarding topological phases have introduced avenues to construct quantum optical systems that are protected against imperfections. For example, the topological transportation of bi-photon state has been realized in a nanophotonics lattice [47]. In addition, using traditional optical elements to control quantum states is very important in modern optical communications and quantum information. Consequently, the robust transportation of multi-photon entangled states by conventional optical devices may possess potential applications in future all-optical quantum network.
In the following, we show that the entangled four photons may be topologically transported using the designed synthetic corner state in the optical cavity. To illustrate this effect, we inject a four-photon state into the designed cavity, where the frequencies, OAMs and polarizations are both entangled. The single-photon state should be selected at four corners in the synthetic space. These four corner states can be expressed as: 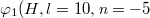 ),
),  ),
), 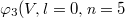 ) and
) and  ). Here, as an example, the input 4-photon entangled state can be written as
). Here, as an example, the input 4-photon entangled state can be written as

where the four photons are correlated with each other, that is, if the 1st photon is in the corner 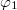 , the 2nd, 3rd and 4th photons must in the corners
, the 2nd, 3rd and 4th photons must in the corners 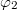 ,
, 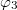 and
and 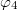 and if the 1st photon is in the corner
and if the 1st photon is in the corner 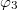 , the 2nd, 3rd and 4th photons must in the corner
, the 2nd, 3rd and 4th photons must in the corner 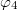 ,
, 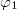 and
and  . In this case, this four-photon state cannot be represented by the direct product of four single-photons and is entangled state. The state of system is time-evolved in the four-photon Hilbert space and we calculated the final steady state based on the coupled mode equation with four photons injection. In fig. 4(a), we plot the numerical result of the output 4-photon steady state with "zero energy" excitation when the systematic parameters are the same to those used in fig. 3(c). It is clearly shown that output photons are still located at the corner in the synthetic space so that both the polarization, OAM and frequency entanglements are preserved with a high fidelity (∼92%, peak value of the output field at the corner in the synthetic space).
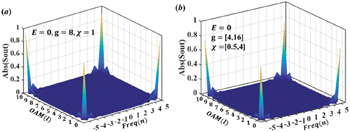
. In this case, this four-photon state cannot be represented by the direct product of four single-photons and is entangled state. The state of system is time-evolved in the four-photon Hilbert space and we calculated the final steady state based on the coupled mode equation with four photons injection. In fig. 4(a), we plot the numerical result of the output 4-photon steady state with "zero energy" excitation when the systematic parameters are the same to those used in fig. 3(c). It is clearly shown that output photons are still located at the corner in the synthetic space so that both the polarization, OAM and frequency entanglements are preserved with a high fidelity (∼92%, peak value of the output field at the corner in the synthetic space).
Fig. 4: The output of injected four-photon entangled states with exciting the synthetic corner state. (a) The steady-state solution of the output four photons state with the value of 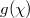 being 8(1). (b) The steady-state modal distribution of output four photons state under the influence of disorder where
being 8(1). (b) The steady-state modal distribution of output four photons state under the influence of disorder where 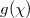 are randomly selected ranging from 4(0.5) to 16(4) on different lattice sites.
are randomly selected ranging from 4(0.5) to 16(4) on different lattice sites.
Download figure:
Standard imageMoreover, when significant disorders are introduced in this synthetic quadrupole topological phase (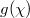 are randomly selected ranging from 4(0.5) to 16(4) on different lattice sites), we find that the output modes of four photons are still mainly concentrated at four corners in the synthetic space (the fidelity is nearly 75%), as shown in fig. 4(b). The configuration average (50 times) has been performed. Consequently, we note that the entangled multi-photon state is robust with disorders within the synthetic quadrupole topological insulators.
are randomly selected ranging from 4(0.5) to 16(4) on different lattice sites), we find that the output modes of four photons are still mainly concentrated at four corners in the synthetic space (the fidelity is nearly 75%), as shown in fig. 4(b). The configuration average (50 times) has been performed. Consequently, we note that the entangled multi-photon state is robust with disorders within the synthetic quadrupole topological insulators.
Discussion the feasibility for the experiment
Although the theoretical aspects of synthetic quadrupole topological insulators are only discussed in the present work, the designed 0D optical cavity with frequency, OAM and polarization controls may be realized in terms of state-of-the-art experiments. In the free-space optics, we may let the central frequency  and the length of the optical cavity L be 100 THz and
and the length of the optical cavity L be 100 THz and 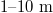 , respectively. The modal spacing and modulation frequency of EOM are both nearly ranging from 10 to
, respectively. The modal spacing and modulation frequency of EOM are both nearly ranging from 10 to 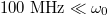 [43]. With such dense modal distribution, the dispersion effect can be neglected for a large number of frequencies of cavity modes. However, it is important to note that losses in our designed system, including transmissions through the input-output channels (mirrors), intrinsic losses associated with reflections on mirrors, modulations in the EOMs and SLMs, can lead to a broadening of the cavity mode, which can make the dense cavity modes become undistinguishable and can also decrease strength of the effective intra-cell/inter-cell couplings in the synthetic space. To solve this problem, the previous experiments [48,49] have shown that we can place a semiconductor optical amplifier in the cavity loops to increase the quality factor (without lasing) of the cavity mode (decrease the linewidth of the cavity mode). It is well known that amplifiers can add noises of spontaneous emission. We can use a dense wavelength-division multiplexing filter to weak the noise. It is worthy to note that due to the high-quality factor of the optical modes, the imperfect frequencies of the different cavities (polarization, OAM and frequency cavities) can make the frequency dimension become invalid and destroy the synthetic quadrupole insulator. So, we must carefully correct the frequency of different cavities.
[43]. With such dense modal distribution, the dispersion effect can be neglected for a large number of frequencies of cavity modes. However, it is important to note that losses in our designed system, including transmissions through the input-output channels (mirrors), intrinsic losses associated with reflections on mirrors, modulations in the EOMs and SLMs, can lead to a broadening of the cavity mode, which can make the dense cavity modes become undistinguishable and can also decrease strength of the effective intra-cell/inter-cell couplings in the synthetic space. To solve this problem, the previous experiments [48,49] have shown that we can place a semiconductor optical amplifier in the cavity loops to increase the quality factor (without lasing) of the cavity mode (decrease the linewidth of the cavity mode). It is well known that amplifiers can add noises of spontaneous emission. We can use a dense wavelength-division multiplexing filter to weak the noise. It is worthy to note that due to the high-quality factor of the optical modes, the imperfect frequencies of the different cavities (polarization, OAM and frequency cavities) can make the frequency dimension become invalid and destroy the synthetic quadrupole insulator. So, we must carefully correct the frequency of different cavities.
On the other hand, to realize the non-trivial coupling conditions 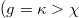 ), the reflectivity of "
), the reflectivity of "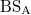 " and "
" and "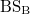 " as well as the modulation strength of EOM
" as well as the modulation strength of EOM 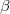 should be suitably tuned to satisfy the relationship of
should be suitably tuned to satisfy the relationship of 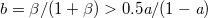 . In the weak modulation range, the recent experiment indicates that
. In the weak modulation range, the recent experiment indicates that 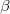 can be set around 0.3. In this case, the ratio between the inter-cell and intra-cell couplings can be expressed as
can be set around 0.3. In this case, the ratio between the inter-cell and intra-cell couplings can be expressed as 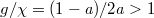 with
with 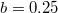 . Hence, we can easily tune the topological gap size by changing the reflectively of
. Hence, we can easily tune the topological gap size by changing the reflectively of 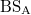 . The most difficult procedure for the realization of corner state is to introduce "boundaries" in the synthetic space since the boundaries are not real. We can follow the previous work to introduce the frequency boundary [43] by coupling with a secondary cavity, which is designed to be resonant with the frequency
. The most difficult procedure for the realization of corner state is to introduce "boundaries" in the synthetic space since the boundaries are not real. We can follow the previous work to introduce the frequency boundary [43] by coupling with a secondary cavity, which is designed to be resonant with the frequency 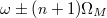 , but to be off-resonant with other modes in between [
, but to be off-resonant with other modes in between [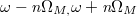 ]. Such a secondary cavity can construct artificial boundaries at
]. Such a secondary cavity can construct artificial boundaries at 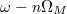 and
and 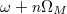 . In addition, the key of creating the OAM boundary is the design of holes in BSs, which should let the
. In addition, the key of creating the OAM boundary is the design of holes in BSs, which should let the 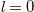 mode pass through with high probability and not significantly affect the
mode pass through with high probability and not significantly affect the 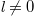 modes [37]. Although the presence of pinhole in BSs may distort the optical modes, which can result in the reduction of effective hopping amplitudes
modes [37]. Although the presence of pinhole in BSs may distort the optical modes, which can result in the reduction of effective hopping amplitudes 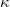 and other unwanted decays, the previous experimental results [37] have shown that they can be relatively small with carefully designed optical devices.
and other unwanted decays, the previous experimental results [37] have shown that they can be relatively small with carefully designed optical devices.
Conclusion
In conclusion, we have theoretically designed the first photonic quadrupole topological insulator in 2D synthetic spaces with the utilization of 0D optical cavities. The coupling between optical cavity modes with different frequencies, OAMs and polarizations are used to fulfill the corresponding tight-binding lattice model in the synthetic space. The numerical results based on the coupled-mode theory demonstrated that the steady-state solution at "zero energy" of the output field from the synthetic quadrupole topological insulator is totally located at the corner of the 2D synthetic spaces even if significant disorders exist. By using the robust corner state in the synthetic spaces, the topological transportation of multi-photon entangled state is proved. Our proposed method may be used to realize many other synthetic higher-order topological phases, such as octupole insulators, quadrupole semimetals and even 4D higher-order topological phases. Moreover, the proposed synthetic corner state may possess potential applications in quantum information processing and offer possibilities for robust shaping of light in synthetic dimensions.
Acknowledgments
This work was supported by the National key R&D Program of China under Grant No. 2017YFA0303800 and the National Natural Science Foundation of China through Grants No. 91850205 and No. 61421001.