Abstract
Motivated by the nonequilibrium dynamics experiment, we study the quantum quench dynamics of the JCH model with weak nearest-neighbor hopping strength by exact diagonalization. One of the crucial insights is to focus on the comparison between the time-averaged density matrix and the canonical ensemble in a wide range of values for the coupling strength between the cavity and the atom, and significant differences are found. Thus, this phenomenon can be used to infer that the system with weak nearest-neighbor hopping strength may be integrable. In order to verify our prediction, we perform the level spacing distribution of the system and find that they conform with the characteristics of the integrable system. Further, a nearly integrable system is presented by removing the degenerate energy level and fitting Brody distribution. Besides, the evolution of the momentum distribution functions of the photon and the equilibrium value predicted by the canonical ensemble are followed, which demonstrates that the system cannot be thermalized. Finally, the way how the system avoids thermalization is also discussed by the finite-size scaling of the fluctuations of the diagonal and the off-diagonal matrix elements.
Export citation and abstract BibTeX RIS
Introduction
With the development and trigger of the fundamental theoretical questions and a surge of experiments [1–5], the nonequilibrium dynamics of many-body quantum systems have received significant attention. One of the protocols to drive a many-body system out of equilibrium is a quantum quench, which means one parameter of the Hamiltonian is changed instantaneously. For such quantum quench, a wealth of interesting problems are triggered by the study of the nonequilibrium dynamics of closed interacting quantum systems. What is the time evolution dynamics of a system deviated from equilibrium? What is universal in the dynamics of integrable systems and nonintegrable systems following a quantum quench? What are the characteristics of the system asymptotic to steady state after the quantum quench? Will the system thermalize after the quantum quench and why a system fail to thermalize even for a long time? In order to answer these questions, several issues have been discussed, including the relaxation of observables, thermalization in the one-dimensional and two-dimensional nonintegrable lattice models [6–15] and the description of the few-body observables relaxing to the time-independent values in integrable systems [16–20]. In the course of the research, some works have shown that integrable systems cannot thermalize [2,7,21–23] and nonintegrable systems may thermalize generally [8,11,22,24–26].
In the theoretical works mentioned above, the models used include the Bose-Hubbard, Fermi-Hubbard, and spin chain models, which only involve the interaction between the same atoms and consider the tunneling of the atom. The purpose of this paper is to extend the analysis to the matter-light system. We focus on the Jaynes-Cummings-Hubbard (JCH) model coupled with photon hopping, which is envisioned as a photonic analogue of an optical lattice in atomic systems. Taking advantage of the competition between the photon blockade effect and hopping, various strongly correlated photons states [27–34] and the Mott insulator-superfluid quantum phase transitions of polaritons [27,29,35–38] can be obtained. The mean-field decoupling [27,29], Monte Carlo [35,36] and variational cluster approaches [37,38] are usually adopted to calculate the phase boundary of the superfluid-insulator transition in two and three dimensions. However, the JCH model is naturally studied under nonequilibrium conditions, as there are invariably photon losses, which appear to be ideally suited to study the nonequilibrium dynamics. Unfortunately, there are few studies on nonequilibrium dynamics for the JCH model after the quantum quench in a large number of theoretical works. In this letter, we study the nonequilibrium quantum quench dynamics of the JCH model with weak nearest-neighbor hopping strength by exact diagonalization [39], which exhibits similar behavior with the integrable system. The evolution of the momentum distribution functions also shows that the system cannot be thermalized.
Jaynes-Cummings-Hubbard model
In the standard Jaynes-Cummings (JC) model, a two-level atom with ground level 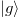 and excited level
and excited level 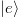 interacts with a single mode of electromagnetic field. The coupling of JC systems in a tight-binding approximation is known as the JCH model. The time-dependent Hamiltonian of the JCH model with the rotating-wave approximation (RWA) reads (
interacts with a single mode of electromagnetic field. The coupling of JC systems in a tight-binding approximation is known as the JCH model. The time-dependent Hamiltonian of the JCH model with the rotating-wave approximation (RWA) reads (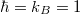 throughout this paper)
throughout this paper)

where  is the photonic creation (annihilation) operator,
is the photonic creation (annihilation) operator,  and
and  are the spin-flip operators between the internal states of the atom (ion) at site j. The parameters
are the spin-flip operators between the internal states of the atom (ion) at site j. The parameters 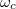 , J and
, J and  are the resonant cavity field frequency, the nearest-neighbor hopping strength of the photon, and the atomic transition energy, respectively. When the parameters
are the resonant cavity field frequency, the nearest-neighbor hopping strength of the photon, and the atomic transition energy, respectively. When the parameters 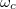 , J and
, J and  are fixed, the dynamic of the system depends only on the time-dependent atom-cavity coupling strength g(t). M is the number of sites. The total number of photonic and atomic excitations is conserved, which can be denoted as
are fixed, the dynamic of the system depends only on the time-dependent atom-cavity coupling strength g(t). M is the number of sites. The total number of photonic and atomic excitations is conserved, which can be denoted as  .
.
Fermion approximation
Every term in Hamiltonian (1) is quadratic and can be usually solved by Fourier transform, especially all cavities are independent as no photon tunneling among them. Meanwhile, the spin operator can be replaced by the fermionic operator because they share the same standard fermionic anticommutation relations. But the breakdown of this simple replacement occurs as the photon tunneling strength increases owing to the indirect coupling between atoms induced by the nonlocality of the photon, namely, on the different sites spin operators obey commutation relations other than anticommutation relations of the fermion. Strictly speaking, this nonlocality can be solved using the Jordan-Wigner transform. Unfortunately, the linear terms in the Hamiltonian (1) bring indelible Jordan-Wigner factors, then the Fourier transform does not work well. Thus, we have to consider the case in which the coupling strength between cavities is weak enough to introduce fermionic approximation securely.
The Hamiltonian (1) can be rewritten as follows in the fermionic approximation [40]:

Here the spin operators 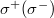 are replaced by fermionic operators
are replaced by fermionic operators 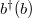 . If the periodic boundary condition is imposed, the Hamiltonian will be invariant under the transform
. If the periodic boundary condition is imposed, the Hamiltonian will be invariant under the transform  ) and
) and 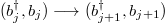 , which indicates that the total quasimomentum
, which indicates that the total quasimomentum  of the system is conserved. Within this approximation, the total quasimomentum of the cavity field is
of the system is conserved. Within this approximation, the total quasimomentum of the cavity field is  (mod
(mod 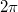 ) and the total quasimomentum of the atom is
) and the total quasimomentum of the atom is 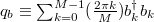 (mod
(mod  ).
). 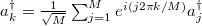 and
and 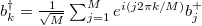 are the creation operators in the k-th Bloch state.
are the creation operators in the k-th Bloch state.
We first restrict to the Hilbert space 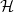 with the total number of excitations N (
with the total number of excitations N (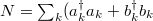 ). The dimension of this space is defined as
). The dimension of this space is defined as

which grows with the system size. Here, the dimension of the Hilbert space of the JCH model grows faster with the increasing system size than the Bose-Hubbard model [41]. For example, 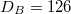 and
and 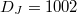 for
for 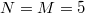 ,
,  and
and 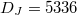 for
for 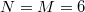 ,
, 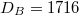 and
and 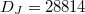 for
for 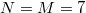 , and
, and 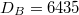 and
and 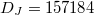 for
for 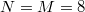 . DB
and DJ
represent the Hilbert space dimensions of the Bose-Hubbard model and the JCH model, respectively.
. DB
and DJ
represent the Hilbert space dimensions of the Bose-Hubbard model and the JCH model, respectively.
We decompose the total Hilbert space  into M subspaces according to the total quasimomentum q of the system, i.e.,
into M subspaces according to the total quasimomentum q of the system, i.e.,  . At this point, the density matrix is always block diagonal with respect to the q subspaces, i.e.,
. At this point, the density matrix is always block diagonal with respect to the q subspaces, i.e., 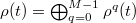 . Because the system behaves quantitatively similarly in all the q subspaces, so one can focus on a specific q subspace. In this paper, we assume that q has a specific value of 1 and take the normalization
. Because the system behaves quantitatively similarly in all the q subspaces, so one can focus on a specific q subspace. In this paper, we assume that q has a specific value of 1 and take the normalization ![$\textrm{Tr}[\rho^{q}(t)] = 1$](https://content.cld.iop.org/journals/0295-5075/134/2/20007/revision1/epl20547ieqn38.gif) [41]. Note that we will remove the subscript q in the following discussion for simplicity.
[41]. Note that we will remove the subscript q in the following discussion for simplicity.
Suppose that the system starts to be in a thermal equilibrium state with temperature Ti
and the parameter gi
. The corresponding Hamiltonian is denoted as Hi
, and the n-th eigenvalue and eigenstate of Hi
are denoted as 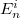 and
and 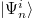 , respectively. The initial density matrix of the whole system is then in the representation of
, respectively. The initial density matrix of the whole system is then in the representation of 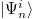 [41]
[41]

where 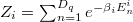 is the partition function and
is the partition function and 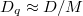 is the dimension of the specific q subspace.
is the dimension of the specific q subspace.
Assume that the system is quenched by changing the coupling strength from gi
to gf
at time 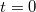 . The Hamiltonian will be denoted as Hf
, and the associated eigenvalues and eigenstates will be denoted as
. The Hamiltonian will be denoted as Hf
, and the associated eigenvalues and eigenstates will be denoted as  and
and 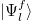 when
when 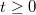 . The density matrix at an arbitrary time is
. The density matrix at an arbitrary time is

where  ,
,  means time ordering. The time-averaged density matrix is defined as
means time ordering. The time-averaged density matrix is defined as

It can be seen that the time-averaged density matrix keeps a memory of the initial state after the quantum quench. Generally, the spectrum is nondegenerate in many models [6–8,42,43]. However, in the JCH model, the spectrum has exact degeneracies in the final Hamiltonian Hf . Therefore, the time-averaged density matrix is



where l labels nondegenerate eigenstates of Hf
and d labels the basis of the degenerate subspaces. In this case, the observable O has off-diagonal matrix elements in the Hf
eigenstate basis. So, we must compute all the overlaps  and
and 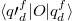 to get time-averaged results for an observable O, where
to get time-averaged results for an observable O, where 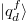 and
and 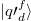 are degenerate states of the degenerate subspaces after the quantum quench [44].
are degenerate states of the degenerate subspaces after the quantum quench [44].
Statistical signatures of the system
Canonical ensemble
When the system has a fixed particle number in thermal equilibrium with a heat bath at some temperature Tc , which can be described using a canonical ensemble (subscript c),

where 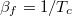 is the final inverse temperature after the quantum quench.
is the final inverse temperature after the quantum quench.
In fig. 1, we focus on the comparison between the time-averaged density matrix  and the canonical ensemble
and the canonical ensemble  as a function of the eigenvalues
as a function of the eigenvalues 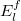 for a wide range of coupling strengths between the cavity field and the atom. The red dots represent the occupation vs. the eigenvalues
for a wide range of coupling strengths between the cavity field and the atom. The red dots represent the occupation vs. the eigenvalues  by
by 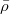 , while the green dots are obtained by
, while the green dots are obtained by  . As can be seen from fig. 1(a), when the coupling strength
. As can be seen from fig. 1(a), when the coupling strength 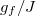 changes abruptly from 10 (the initial coupling strength) to 11, there is a tiny difference between
changes abruptly from 10 (the initial coupling strength) to 11, there is a tiny difference between 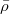 and
and 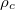 . In the cases of
. In the cases of 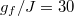 and
and  , the distribution of the time-averaged density matrix
, the distribution of the time-averaged density matrix  and canonical ensemble
and canonical ensemble 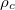 are similar, i.e., a linear variation with
are similar, i.e., a linear variation with 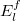 , but they are in a bad agreement. On the other hand, further numerical results show that the discrepancy of the distribution between the time-averaged density matrix and the canonical ensemble ones can be diminished remarkably as
, but they are in a bad agreement. On the other hand, further numerical results show that the discrepancy of the distribution between the time-averaged density matrix and the canonical ensemble ones can be diminished remarkably as 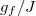 is close to the initial value
is close to the initial value 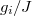 , and conversely, the larger the deviation. These results are also related to whether the inverse temperature
, and conversely, the larger the deviation. These results are also related to whether the inverse temperature  approaches the initial inverse temperature
approaches the initial inverse temperature 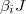 . It can also be seen from fig. 1 that the density of states exhibits surprising symmetry no matter how large the value of
. It can also be seen from fig. 1 that the density of states exhibits surprising symmetry no matter how large the value of 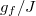 takes after the quantum quench, which also shows a good correspondence with the results obtained from the time-averaged density matrix. It also can be found, in figs. 1(b) and (c), that the density of states located at the edges of the spectrum is small, and the red dots are less. The density of states approaches to the peak at the center of the spectrum, and the red dots are more. In addition, at some fixed locations of the spectrum, the density of states and the time-averaged density matrix will appear or disappear simultaneously as shown in fig. 1(d). In the entire spectrum, there are many local peaks in the density of states, which indicates that the localization properties of photons and atoms are very strong, and the system shows the characteristics of bound states. Based on the analysis mentioned above, one knows that it is a failure to describe the JCH system using a canonical ensemble with a small nearest-neighbor hopping strength, which suggests that the JCH system within the parameters under consideration may be an integrable one.
takes after the quantum quench, which also shows a good correspondence with the results obtained from the time-averaged density matrix. It also can be found, in figs. 1(b) and (c), that the density of states located at the edges of the spectrum is small, and the red dots are less. The density of states approaches to the peak at the center of the spectrum, and the red dots are more. In addition, at some fixed locations of the spectrum, the density of states and the time-averaged density matrix will appear or disappear simultaneously as shown in fig. 1(d). In the entire spectrum, there are many local peaks in the density of states, which indicates that the localization properties of photons and atoms are very strong, and the system shows the characteristics of bound states. Based on the analysis mentioned above, one knows that it is a failure to describe the JCH system using a canonical ensemble with a small nearest-neighbor hopping strength, which suggests that the JCH system within the parameters under consideration may be an integrable one.
Fig. 1: Comparison of diagonal elements of different ensembles 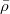 (red dots) with
(red dots) with 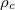 (green dots) vs. the eigenvalues El
for different quenches. In this paper, the initial atom-cavity coupling strength
(green dots) vs. the eigenvalues El
for different quenches. In this paper, the initial atom-cavity coupling strength 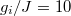 is our energy scale and we set
is our energy scale and we set 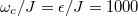 and J = 1. The other parameters are
and J = 1. The other parameters are 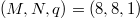 ,
, 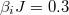 . The top of each plot contains the quenched values of g/J and the fitting inverse temperatures
. The top of each plot contains the quenched values of g/J and the fitting inverse temperatures 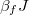 . The black lines at the bottom depict the coarse-grained density of states of Hf
.
. The black lines at the bottom depict the coarse-grained density of states of Hf
.
Download figure:
Standard imageLevel spacing distribution
In order to identify whether the system is integrable, we analyze the level spacing distribution P(s) with the spacing s of the neighboring energy levels. The form of the distribution depends on the symmetry properties of the Hamiltonian. The quantum levels of integrable systems are not correlated and levels may cross, so the distribution is Poissonian. In nonintegrable systems, crossings are avoided and the level spacing distribution is given by the Gaussian orthogonal ensembles or the Gaussian unitary ensembles. The results of the level spacing distribution with weak nearest-neighbor hopping strength are shown in figs. 2(a)–(d) for a wide range of values of g/J (condition 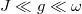 is satisfied), which shows that the level spacing distribution has similar features and approximates to the characteristics of Poisson distribution due to a large number of degenerates and small interval of the system eigenvalues. Thus, this also explains the reasons that the time-averaged density matrix does not fall close to the canonical ensemble after the quantum quench as shown in fig. 1. Actually, the JCH model can be solved analytically for weak nearest-neighbor hopping strength [40], therefore the results obtained here also agree with this conclusion. In order to further confirm whether the system can be integrable, we remove the degenerate energy level and display the Brody distribution in figs. 2(e)–(h).
is satisfied), which shows that the level spacing distribution has similar features and approximates to the characteristics of Poisson distribution due to a large number of degenerates and small interval of the system eigenvalues. Thus, this also explains the reasons that the time-averaged density matrix does not fall close to the canonical ensemble after the quantum quench as shown in fig. 1. Actually, the JCH model can be solved analytically for weak nearest-neighbor hopping strength [40], therefore the results obtained here also agree with this conclusion. In order to further confirm whether the system can be integrable, we remove the degenerate energy level and display the Brody distribution in figs. 2(e)–(h).
Fig. 2: Level spacing distribution for the Hamiltonian. The top of each plot contains the values of g/J and α. Other parameters have the same values as in fig. 1. The red lines are the theoretical curves of the Brody distribution.
Download figure:
Standard imageGenerally, the expression of the Brody distribution is

In the strongly integrable regime 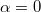 we observe Poissonian statistics while in the completely chaotic one
we observe Poissonian statistics while in the completely chaotic one 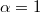 . Thus, the system is close to an integrable system with the parameters considered as shown in figs. 2(e)–(h).
. Thus, the system is close to an integrable system with the parameters considered as shown in figs. 2(e)–(h).
Time evolution
In this section, we focus on the momentum distribution function of the photon,

and similarly for the atom 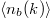 , which are usually measured in experiments with ultracold quantum gases via time-of-flight expansion. a is a lattice spacing. Let
, which are usually measured in experiments with ultracold quantum gases via time-of-flight expansion. a is a lattice spacing. Let 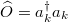 . The time evolution of the quantum expectation value of an observable na
(k) (similarly for nb
(k)) can be written as
. The time evolution of the quantum expectation value of an observable na
(k) (similarly for nb
(k)) can be written as

where 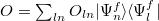 . And its time-averaged value is
. And its time-averaged value is

Figure 3 shows results for 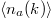 (
( has similar behavior) as a function of time t for different quenches. Interestingly, the time evolution of
has similar behavior) as a function of time t for different quenches. Interestingly, the time evolution of 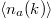 in figs. 3(a)–(d) shows similar behavior for all values of
in figs. 3(a)–(d) shows similar behavior for all values of 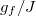 . First, in all cases, there is an oscillation of
. First, in all cases, there is an oscillation of 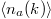 near the time-averaged density matrix, and its frequency increases when the post-quench interaction strength is enhanced. These results can be viewed based on eq. (13) as follows. The frequency of the oscillation depends on the difference between the spectrum of the post-quench Hamiltonian. The level spacing becomes large as
near the time-averaged density matrix, and its frequency increases when the post-quench interaction strength is enhanced. These results can be viewed based on eq. (13) as follows. The frequency of the oscillation depends on the difference between the spectrum of the post-quench Hamiltonian. The level spacing becomes large as 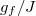 increases as shown in fig. 1. Thus, for
increases as shown in fig. 1. Thus, for 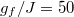 , the frequency of the oscillation is faster than the one for
, the frequency of the oscillation is faster than the one for  . Second, the values of the time-averaged density matrix are very similar for different k, even though the post-quench interaction strengths are clearly different, while the predictions of the canonical ensembles vary widely. Third, the interesting phenomenon is that the deviation between the canonical ensemble and the time-averaged density matrix is more pronounced with
. Second, the values of the time-averaged density matrix are very similar for different k, even though the post-quench interaction strengths are clearly different, while the predictions of the canonical ensembles vary widely. Third, the interesting phenomenon is that the deviation between the canonical ensemble and the time-averaged density matrix is more pronounced with 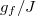 increasing, which also means thermalization is absent. This is consistent with the separation between
increasing, which also means thermalization is absent. This is consistent with the separation between  and
and  for different quenches, as revealed in fig. 1. The last phenomenon is that the frequency of the oscillation with wave vector k = 2 is especially small for all cases.
for different quenches, as revealed in fig. 1. The last phenomenon is that the frequency of the oscillation with wave vector k = 2 is especially small for all cases.
Fig. 3: Time evolution of the populations on the Bloch states  . Each panel has the same parameters as the ones in fig. 1, respectively. From top to bottom, the five lines correspond to
. Each panel has the same parameters as the ones in fig. 1, respectively. From top to bottom, the five lines correspond to 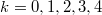 in each plot. There,
in each plot. There, 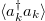 and
and  are close to each other all the time. The average values predicted by
are close to each other all the time. The average values predicted by 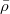 (stars) and
(stars) and 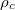 (squares) on the right-hand side are also shown for each line, respectively.
(squares) on the right-hand side are also shown for each line, respectively.
Download figure:
Standard imageDiscussion of the ETH
In order to understand the reasons that the canonical ensemble fails to describe the JCH system with weak nearest-neighbor hopping strength after the quantum quench, it is instructive to revisit the validity of the ETH for this model. To that end, the expectation values of na
(k) and nb
(k) are calculated numerically in all eigenstates 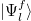 of the post-quench Hamiltonian. In fig. 4, the distribution restricted to the wave vector k = 0 is depicted.
of the post-quench Hamiltonian. In fig. 4, the distribution restricted to the wave vector k = 0 is depicted.
Firstly, some interesting issues are needed to be illustrated. An important requirement for the ETH is that the expectation value of a generic few-body physical quantity is a smooth function of energy. In other words, the difference of the average of the physical observable between different eigenstates is small. Figure 4 shows that the fluctuations of 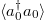 and
and 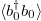 are very large over the entire spectrum after the quantum quench and ETH does not hold. This is consistent with the results achieved in figs. 1 and 3, i.e., the canonical ensemble cannot be used to describe this quenched system within the chosen parameters and thermalization cannot occur. Furthermore, the distributions of
are very large over the entire spectrum after the quantum quench and ETH does not hold. This is consistent with the results achieved in figs. 1 and 3, i.e., the canonical ensemble cannot be used to describe this quenched system within the chosen parameters and thermalization cannot occur. Furthermore, the distributions of 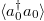 and
and  are very broad and structured for different
are very broad and structured for different 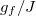 in most regions of the spectrum, which shows consistent behavior with integrable system or systems that are close to an integrable point in the lower part of the spectrum [6,7].
in most regions of the spectrum, which shows consistent behavior with integrable system or systems that are close to an integrable point in the lower part of the spectrum [6,7].
Fig. 4:
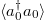 and
and 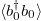 as a function of the energy for the eigenstates of the Hamiltonian. Each panel has the same parameters as the ones in fig. 1. Blue
as a function of the energy for the eigenstates of the Hamiltonian. Each panel has the same parameters as the ones in fig. 1. Blue 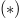 shows eigenstate expectation values of
shows eigenstate expectation values of  . Orange (+) shows eigenstate expectation values of
. Orange (+) shows eigenstate expectation values of  .
.
Download figure:
Standard imageNext, we discuss the finite-size scaling of the fluctuations of diagonal and off-diagonal matrix elements. The following results are the same for other 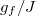 .
.
Diagonal matrix elements of observables
In the k = 0 quasimomentum sector for three different system sizes M = 6, 7, 8, we plot the results for observables  vs. the eigenstate energy density
vs. the eigenstate energy density 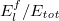 in figs. 5(a)–(d). The results show the widths of the matrix-element distribution of
in figs. 5(a)–(d). The results show the widths of the matrix-element distribution of  in the middle of the spectrum become larger as the system size M increases. Therefore, these results violate the validity of ETH (the eigenstate-expectation values will become a smooth and sharp function of the energy density when M tends to infinity).
in the middle of the spectrum become larger as the system size M increases. Therefore, these results violate the validity of ETH (the eigenstate-expectation values will become a smooth and sharp function of the energy density when M tends to infinity).
In addition, the key step to verify the validity of ETH is to analyze the fluctuations of the diagonal elements of observables with the finite-size scaling. The validity of ETH means that the eigenstate-to-eigenstate fluctuations will disappear when M tends to infinity. Therefore, we analyse eigenstate-to-eigenstate fluctuations vs. the size of the system in the bulk of the spectrum. A measure of eigenstate-to-eigenstate fluctuations of diagonal expectation values [45] is

In a narrow energy window around  (with a control parameter
(with a control parameter ![$\eta\in[0, 1]$](https://content.cld.iop.org/journals/0295-5075/134/2/20007/revision1/epl20547ieqn120.gif) ), the mean is defined as
), the mean is defined as

where  is the number of eigenstates in
is the number of eigenstates in  ,
, 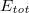 and η are defined as follows:
and η are defined as follows:



we fix 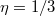 . Therefore, the corresponding set of eigenstates are limited to the above target energy-density window.
. Therefore, the corresponding set of eigenstates are limited to the above target energy-density window.
Figure 5(d) shows the finite-size scaling of 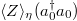 . We observe that the fluctuations hardly decrease as the system size increases. This result violates the validity of ETH, where the fluctuations will decrease exponentially with increasing size. The behavior shown in fig. 5(d) is in accord with one of the diagonal elements of the integrable system [46] and violates the diagonal part of the ETH ansatz in our model.
. We observe that the fluctuations hardly decrease as the system size increases. This result violates the validity of ETH, where the fluctuations will decrease exponentially with increasing size. The behavior shown in fig. 5(d) is in accord with one of the diagonal elements of the integrable system [46] and violates the diagonal part of the ETH ansatz in our model.
Fig. 5: Diagonal matrix elements of observables  for
for 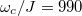 ,
, 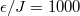 ,
, 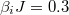 and J = 1 in the quasimomentum sector q = 1. Results are plotted as a function of the rescaled energy for the eigenstates of the Hamiltonian, where the energy
and J = 1 in the quasimomentum sector q = 1. Results are plotted as a function of the rescaled energy for the eigenstates of the Hamiltonian, where the energy  is defined in eq. (17). The other parameters are in the upper right corner of the figure. The mean statistics of eigenstate-to-eigenstate fluctuations
is defined in eq. (17). The other parameters are in the upper right corner of the figure. The mean statistics of eigenstate-to-eigenstate fluctuations  is plotted vs. the system size.
is plotted vs. the system size.
Download figure:
Standard imageOffdiagonal matrix elements of observables
Figures 6(a)–(c) shows the off-diagonal matrix elements of observable 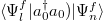 as a function of the eigenenergy difference
as a function of the eigenenergy difference 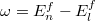 (we only plot results for
(we only plot results for  ) in a narrow energy window around
) in a narrow energy window around 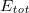 . We observe that the off-diagonal matrix elements of the observable have strong fluctuations, and the fluctuations increase rapidly with the system size. In addition, the running average (black line) of those elements oscillates, but it does not show a downward trend. This is different from the running average of the off-diagonal matrix element that satisfies ETH (the running average is almost flat at small ω and then rapidly decays at larger ω in the nonintegrable case [12]). In fig. 6(d) we present such a plot for the average between the off-diagonal matrix elements of eigenstates with
. We observe that the off-diagonal matrix elements of the observable have strong fluctuations, and the fluctuations increase rapidly with the system size. In addition, the running average (black line) of those elements oscillates, but it does not show a downward trend. This is different from the running average of the off-diagonal matrix element that satisfies ETH (the running average is almost flat at small ω and then rapidly decays at larger ω in the nonintegrable case [12]). In fig. 6(d) we present such a plot for the average between the off-diagonal matrix elements of eigenstates with  . The numerical results do not exhibit an excellent agreement with
. The numerical results do not exhibit an excellent agreement with 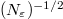 behavior, which does not satisfy the nondiagonal part of ETH ansatz.
behavior, which does not satisfy the nondiagonal part of ETH ansatz.
Fig. 6: Absolute value of the off-diagonal matrix elements of 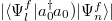 in the eigenenergy basis, in a narrow energy window around
in the eigenenergy basis, in a narrow energy window around 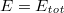 (with a width of 0.1) vs. the eigenenergy difference
(with a width of 0.1) vs. the eigenenergy difference  . The other parameters are in the lower right corner of the figure. The black lines are running averages with a subset length of 20 for
. The other parameters are in the lower right corner of the figure. The black lines are running averages with a subset length of 20 for 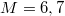 and 100 for M = 8. The average of the absolute value of the off-diagonal matrix elements of observables
and 100 for M = 8. The average of the absolute value of the off-diagonal matrix elements of observables  is plotted vs. the number of eigenstates
is plotted vs. the number of eigenstates 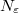 .
.
Download figure:
Standard imageConclusion
The quench dynamics and thermalization of the JCH model with a weak nearest-neighbor hopping strength are explored by the exact diagonalization. First, we calculate the time-averaged density matrix of the system after a quench from an initial state and compare it with the canonical ensemble. The results show that the canonical ensemble is not consistent with the time-averaged density matrix, and this discrepancy becomes more pronounced with the increasing of the quenching strength. Second, the energy spectrum of the system reveals that a large number of levels cross, which is close to the level spacing distribution of the integrable system. By removing the degenerate energy level and fitting Brody distribution, a nearly integrable system is presented. We further study the evolution of the momentum distribution functions about the photon and the equilibrium values predicted by the canonical ensemble, and find that the system cannot be thermalized in a wide range of values for the coupling strength between the cavity field and the atom. Finally, we discuss the finite-size scaling of the fluctuations of diagonal and off-diagonal matrix elements, which indicate the way how the system avoids thermalization.
The above results are all discussed within the conditions of the weak nearest-neighbor hopping strength. Due to the numerical study of eq. (2), the nonergodic behavior discussed may well be a finite-size effect due to the small system sizes. And then the absence of thermalization in the Hamiltonian equation (2) does not imply absence of thermalization in the more general form eq. (1), even for identical parameters. For other parameters, the JCH system may exhibit quantum chaotic property and obey ETH. Therefore, the quenched dynamics of the JCH without fermionic approximation is expected to be investigated in the future.
Acknowledgments
This work was supported by NSFC under grant No. 11874190. We thank J. M. Zhang for useful discussions.











