Abstract
In ice speed skating, the friction between the steel skate blade and the ice stems from boundary friction where the temperature of the interface is below zero and ice surface molecules exhibit unconventional mobility, and hydrodynamic friction where the ice melts and a thin water layer between the blade and the ice forms. An analytical solution of the steady-state lubrication equation shows that the boundary friction only plays a role at the tip of the skate blade over an extremely short contact length between the skate blade and the ice. Albeit its negligible contribution to total friction, boundary friction generates enough heat to melt the ice which allows the skater to slide smoothly on a thin layer of melt water. It is also shown that the precise value of the boundary friction coefficient is not important for speed skate friction because it works only over an extremely short contact length.
Export citation and abstract BibTeX RIS

Published by the EPLA under the terms of the Creative Commons Attribution 4.0 International License (CC-BY). Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.
Introduction
Speed skating is possible because there exists a very thin liquid layer between the ice surface and the steel skate blade. Although this notion has largely been accepted [1], the question about the origin of this layer is still open. Already in 1859, Faraday [2] postulated the existence of a liquid layer that forms on ice below the bulk melting point (pre-melting), even without the contact of any other body. The layer thickness typically is on the order of a few molecular layers [3] and boundary friction coefficients on the order  were reported [4–8]. Recent experiments show a complex viscoelastic rheology of the pre-melting water film in the boundary friction regime [9], and a strong functional dependence of the friction coefficient on the temperature [10]. While the existence of this layer explains the fact that a steel slider does not freeze to the ice at standstill, it does not explain the low friction coefficients (4–
were reported [4–8]. Recent experiments show a complex viscoelastic rheology of the pre-melting water film in the boundary friction regime [9], and a strong functional dependence of the friction coefficient on the temperature [10]. While the existence of this layer explains the fact that a steel slider does not freeze to the ice at standstill, it does not explain the low friction coefficients (4– ) measured during actual speed skating [11] at high velocities (10 m/s). Bowden and Hughes [12] were the first to suggest that a thin layer of melt water between the ice surface and the skate blade caused by frictional heating could be responsible for the low friction coefficient on ice. Kietzig et al. [7] extensively reviewed surface melting theories responsible for the development of such a lubrication layer and the various laboratory setups for ice friction measurements. More recently, Persson [13] considered the role of non-uniform frictional heating where the ice melts in asperity contact regions, as was also discussed by Oksanen [14]. Asperities also play an important role in rubber-ice friction to improve tyre grip performance [15].
) measured during actual speed skating [11] at high velocities (10 m/s). Bowden and Hughes [12] were the first to suggest that a thin layer of melt water between the ice surface and the skate blade caused by frictional heating could be responsible for the low friction coefficient on ice. Kietzig et al. [7] extensively reviewed surface melting theories responsible for the development of such a lubrication layer and the various laboratory setups for ice friction measurements. More recently, Persson [13] considered the role of non-uniform frictional heating where the ice melts in asperity contact regions, as was also discussed by Oksanen [14]. Asperities also play an important role in rubber-ice friction to improve tyre grip performance [15].
We argue here that during ice speed skating i) the low friction on ice is caused by the presence of a lubrication layer of melt water between the slider and the ice, that ii) the contribution of boundary friction to the total friction is negligible irrespective of its actual value and that iii) the contribution of boundary friction is essential to generate enough heat to melt the ice. If enough frictional heat is generated, at some distance along the contact length between the slider and the ice, the melting point of ice will be reached and a transition from boundary friction to hydrodynamic shearing will occur, which immediately reduces the friction coefficient. Hydrodynamic shearing is generally acknowledged in sport skating literature [8,16,17] to explain ice friction, but less attention is paid to boundary friction. We will show here that both boundary friction and hydrodynamic shearing are needed to sketch the complete picture of the lubrication layer and its onset. We now specify that the contact length extends from the first point of contact x = 0 between the blade and the ice to the point of maximum penetration of the blade into the ice at x = L (see fig. 1). The underside of the skate blade is curved with a radius of curvature of 25 m. This curvature is often referred to as the rocker of the skate blade. Lozowski and Szilder [16] used the force balance between the weight of the skater (gliding upright on one skate every stroke) and the so-called hardness of the ice to determine L. For a blade width d of 1.1 mm, a skater mass of 75 kg, and an ice temperature of  , they found
, they found  cm and a skate track depth of some
cm and a skate track depth of some  . As
. As 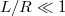 , we take the underside of the blade horizontal in the forthcoming derivations. We remark that due to the curvature of the underside of the blade, only a fraction (3.75 cm) of the total length
, we take the underside of the blade horizontal in the forthcoming derivations. We remark that due to the curvature of the underside of the blade, only a fraction (3.75 cm) of the total length  of the blade, which is typically 40 cm long, is in contact with the ice. This long length
of the blade, which is typically 40 cm long, is in contact with the ice. This long length 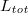 allows the blade to stay on the ice longer during each stride thus increasing the pushing power. During a stride, the contact area unreels over the underside of the blade. The use of clap skates developed by Gerrit Jan van Ingen Schenau at the Faculty of Human Movement Sciences of the Vrije Universiteit of Amsterdam, Netherlands, allows even longer contact times.
allows the blade to stay on the ice longer during each stride thus increasing the pushing power. During a stride, the contact area unreels over the underside of the blade. The use of clap skates developed by Gerrit Jan van Ingen Schenau at the Faculty of Human Movement Sciences of the Vrije Universiteit of Amsterdam, Netherlands, allows even longer contact times.
Fig. 1: Schematic configuration (not to scale) of curved skate blade in contact with moving ice layer underneath. The radius of curvature is 25 m.
Download figure:
Standard imageBoundary friction
Let us first assume that no melting occurs and that the friction between the ice and the slider is described by the boundary friction coefficient μ. The heat flux at the interface into the ice is given by

where the weight of the skater is FN and f is the fraction of the heat that flows into the ice. The ice temperature in degrees Celsius T(x) at the interface is given by ([18], p. 151):

where k, ρ and c are the thermal conductivity, density and specific heat of the ice, respectively. 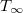 is the temperature of the ice far away from the interface. Note that
is the temperature of the ice far away from the interface. Note that  . Because of the frictional heat, T(x) will increase for increasing x until the melting temperature is reached at
. Because of the frictional heat, T(x) will increase for increasing x until the melting temperature is reached at  :
:

By substituting q1 from (1) into (3), we obtain for the position of first melting:

Based on measurements in the Calgary Olympic Oval, Lozowski et al. [17] estimated the amount of heat conducted into or from the blade itself and concluded that it is negligible for ice speed skating indoors. In the Supplementary Material
Supplementarymaterial.pdf
we prove that this is a realistic assumption indeed. Hence we shall take f = 1 in the forthcoming. Under typical ice speed skating conditions (table 1) we find that 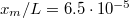 , so that only a very small part of the slider experiences boundary friction. The rest of the slider will experience hydrodynamic friction where the ice has melted. A totally different friction regime was explored by Weber et al. [10] and Bäurle et al. [19]. Weber et al. used a rigid ball (
, so that only a very small part of the slider experiences boundary friction. The rest of the slider will experience hydrodynamic friction where the ice has melted. A totally different friction regime was explored by Weber et al. [10] and Bäurle et al. [19]. Weber et al. used a rigid ball (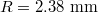 ) sliding over the ice with a velocity of 0.38 mm/s, under a normal force
) sliding over the ice with a velocity of 0.38 mm/s, under a normal force  , at an ice temperature
, at an ice temperature  . The Hertzian contact area in that case is
. The Hertzian contact area in that case is  ([10], supporting information). They measured
([10], supporting information). They measured 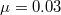 . Using our equation (4), we estimate
. Using our equation (4), we estimate 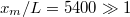 in that case, which means that there is no melting of ice and pure boundary friction is measured. Also the experiments by Bäurle et al. [19] are in the pre-melting regime. Substituting their values
in that case, which means that there is no melting of ice and pure boundary friction is measured. Also the experiments by Bäurle et al. [19] are in the pre-melting regime. Substituting their values 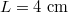 ,
, 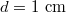 (contact area
(contact area 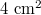 ), velocity
), velocity  , load
, load 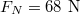 ,
, 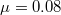 at an ice temperature of
at an ice temperature of 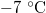 , in our equation (4), we find
, in our equation (4), we find 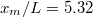 , so that not enough heat is generated to melt the ice. We finally remark that the precise value of μ is not so relevant for ice skating. Even in the unlikely situation in which
, so that not enough heat is generated to melt the ice. We finally remark that the precise value of μ is not so relevant for ice skating. Even in the unlikely situation in which 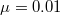 ,
, 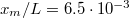 , so that the contribution of dry boundary friction can still be neglected.
, so that the contribution of dry boundary friction can still be neglected.
Table 1:. Parameter overview.
| Friction coefficient | μ | 0.1 | |
| Ice temperature |

| –5 | °C |
| Slider length | L | 37.5 | mm |
| Slider width | d | 1.1 | mm |
| Velocity | V | 10 | m/s |
Water viscosity at  C C | η | 1.79 | mPa.s |
| Normal force | FN | 750 | N |
| Thermal conductivity of ice | k | 2.2 | W/m/K |
| Water density |
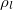
| 1000 | kg/m3 |
| Ice density | ρ | 918 | kg/m3 |
| Heat capacity of ice | c | 2027 | J/kg/K |
| Melting heat of ice | lm | 333 | kJ/kg |
For xm
< x < L, the temperature of the ice at the interface will remain 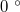 C, and the asymptotic solution which is exact for
C, and the asymptotic solution which is exact for  is then ([18], p. 151):
is then ([18], p. 151):

where we determine xc
from (3) and (5) because the heat fluxes are assumed to be continuous at 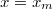 :
:

Dividing (3) by (5), we find that

Two distinct regions are thus identified: the region near the point of first contact (0 < x < xm ) with constant heat flux q into the cold ice, and the slider region xm < x < L where the interface temperature is constant, melting occurs, a lubrication water layer is formed between slider and ice, and hydrodynamic friction occurs.
Hydrodynamic friction
We shall now assume that the hydrodynamic friction sets in at 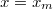 , and that instantaneously the tangential force at the interface equals its Newtonian value
, and that instantaneously the tangential force at the interface equals its Newtonian value 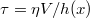 , with η the viscosity of liquid water and h(x) the thickness of the lubrication layer. Wu et al. [20] studied the
, with η the viscosity of liquid water and h(x) the thickness of the lubrication layer. Wu et al. [20] studied the  dependency in capillary tubes, and found negligible effects above 10 nm, for small contact angles (typical for ice-water interfaces). The heat flux generated by the Couette flow in the lubrication layer then is
dependency in capillary tubes, and found negligible effects above 10 nm, for small contact angles (typical for ice-water interfaces). The heat flux generated by the Couette flow in the lubrication layer then is  . As the heat flux into the dry ice is q2, there is
. As the heat flux into the dry ice is q2, there is 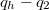 available for melting the ice which causes the water layer to grow thicker for increasing x. The mass increase rate in the water layer per unit interface area is
available for melting the ice which causes the water layer to grow thicker for increasing x. The mass increase rate in the water layer per unit interface area is 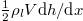 , with
, with 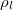 the water density. Note the factor
the water density. Note the factor 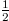 because of the linear Couette flow profile. Energy conservation now dictates that:
because of the linear Couette flow profile. Energy conservation now dictates that:

with lm
the latent heat of melting. We note from (3) that  , so that the lubrication equation becomes
, so that the lubrication equation becomes

with 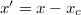 ,
, 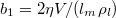 and
and  . Comparing this relation with the lubrication equation by Lozowski et al. ([17], eq. (17)), we notice that there is a factor 2 discrepancy both in the frictional melting (b1) and the heat conduction (b2). This is because in their model the plug flow is assumed instead of the Couette flow. We also note that Lozowski's lubrication equation has an additional term that takes liquid squeezing into account. We will neglect that term for the moment in order to facilitate an analytical solution of the lubrication equation. Setting
. Comparing this relation with the lubrication equation by Lozowski et al. ([17], eq. (17)), we notice that there is a factor 2 discrepancy both in the frictional melting (b1) and the heat conduction (b2). This is because in their model the plug flow is assumed instead of the Couette flow. We also note that Lozowski's lubrication equation has an additional term that takes liquid squeezing into account. We will neglect that term for the moment in order to facilitate an analytical solution of the lubrication equation. Setting

eq. (9) is brought in the separable form

where 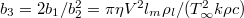 . This dimensionless group relates frictional melting and heat conduction. The left-hand side of (11) is subsequently integrated from
. This dimensionless group relates frictional melting and heat conduction. The left-hand side of (11) is subsequently integrated from 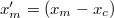 to
to 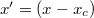 and the right-hand side from 0 to u:
and the right-hand side from 0 to u:

where 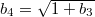 . Rearranging terms, the above expression can be rewritten as
. Rearranging terms, the above expression can be rewritten as

We note that 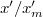 goes to infinity for
goes to infinity for 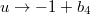 where the denominator of the first term on the right-hand side equals zero. From (10) it is now clear that the reduced water layer thickness
where the denominator of the first term on the right-hand side equals zero. From (10) it is now clear that the reduced water layer thickness 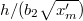 asymptotically approaches
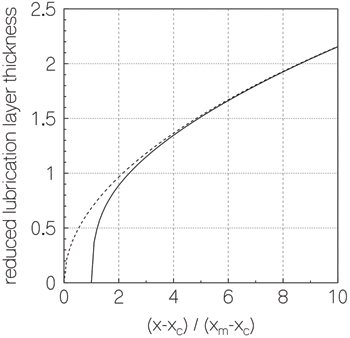
asymptotically approaches 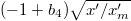 . A plot of the reduced lubrication layer thickness as a function of the position along the slider is given in fig. 2. The lubrication layer thickness catches up with the asymptotic solution within a very short distance from the point of first contact. In this very short interval boundary friction is dominant and enough heat is generated to melt the ice and trigger the lubrication layer. For the friction force we have that
. A plot of the reduced lubrication layer thickness as a function of the position along the slider is given in fig. 2. The lubrication layer thickness catches up with the asymptotic solution within a very short distance from the point of first contact. In this very short interval boundary friction is dominant and enough heat is generated to melt the ice and trigger the lubrication layer. For the friction force we have that 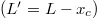

and a friction factor  is defined accordingly. Simply integrating all terms in (9) from
is defined accordingly. Simply integrating all terms in (9) from 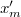 to
to 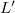 , we find that
, we find that

so that

For  , an accurate estimate is found by substitution of the asymptotic approximation for the water layer thickness
, an accurate estimate is found by substitution of the asymptotic approximation for the water layer thickness 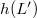 :
:

Using the parameters of table 1 for a speed of 10 m/s, we find from (1) that 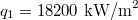 and from (4) that
and from (4) that 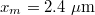 , so that the ice starts to melt almost immediately behind the slider tip. From (17) we find that
, so that the ice starts to melt almost immediately behind the slider tip. From (17) we find that 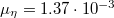 , so that the total friction factor
, so that the total friction factor  equals
equals 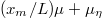 =
= 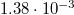 . We remark that the contribution of boundary friction to the total friction coefficient is negligible.
. We remark that the contribution of boundary friction to the total friction coefficient is negligible.
Fig. 2: Reduced lubrication layer thickness 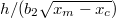 (solid line) and asymptotic solution (dashed line) vs. the position along the blade. The position of first melting
(solid line) and asymptotic solution (dashed line) vs. the position along the blade. The position of first melting  . In a very short interval boundary friction generates enough heat to melt the ice and trigger the lubrication layer.
. In a very short interval boundary friction generates enough heat to melt the ice and trigger the lubrication layer.
Download figure:
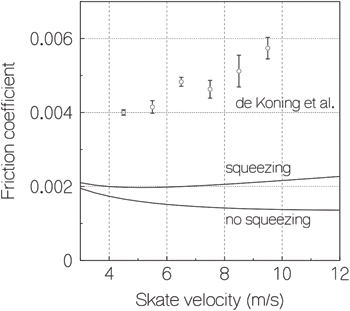
Standard imageIn fig. 4, we compare our theory with experimental data by de Koning et al. [11]. The measurements suggest that the theory is still incomplete. An additional squeeze flow mechanism was therefore proposed by Lozowski et al. [16,17].
Squeeze flow
It can be argued that water is squeezed out from under the blade as a result of the pressure applied by the weight of the skater, resulting in a thinner lubrication layer and thus more friction. Following Lozowski and Szilder [16], an extra term is consequently added to the lubrication equation:

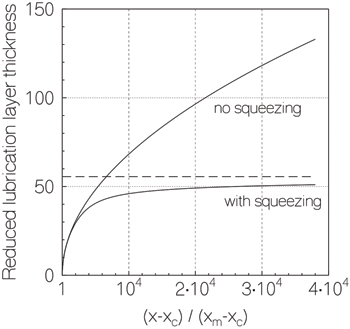
with  . This differential equation is solved numerically using the Runge-Kutta method. The resulting lubrication layer thickness is plotted in fig. 3. It can be seen that the lubrication layer becomes much thinner, especially towards the end of the slider, approaching its asymptotic value
. This differential equation is solved numerically using the Runge-Kutta method. The resulting lubrication layer thickness is plotted in fig. 3. It can be seen that the lubrication layer becomes much thinner, especially towards the end of the slider, approaching its asymptotic value 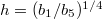 . The expression for the viscous friction coefficient becomes
. The expression for the viscous friction coefficient becomes

where the integral on the right-hand side is numerically evaluated with the trapezoidal rule. The result is also plotted in fig. 4. We note that water squeezing increases the fiction indeed, and that there is minimum friction around 5 m/s skate speed. Yet, the measured friction is still higher. Lozowski and Szilder [16] thus included an additional ploughing force in their model which added 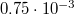 to the computed friction coefficient and later also took slider blade inclination into account [17]. In this way, a good agreement with the de Koning's measurements was obtained.
to the computed friction coefficient and later also took slider blade inclination into account [17]. In this way, a good agreement with the de Koning's measurements was obtained.
Fig. 3: Reduced lubrication layer thickness 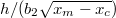 vs. the position along the contact zone
vs. the position along the contact zone 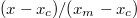 . The lubrication layer at the end of the slider is
. The lubrication layer at the end of the slider is  thick without squeezing and only
thick without squeezing and only 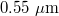 with squeezing. The dashed line is the asymptote
with squeezing. The dashed line is the asymptote 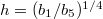 .
.
Download figure:
Standard imageFig. 4: Friction coefficient with and without squeezing as a function of the skate velocity compared with measurement data by de Koning et al. [11].
Download figure:
Standard imageConclusions
We revisited ice speed skating from the perspective of a Couette flow where the blade is fixed and the ice is moving with constant speed. The friction between the skate blade and the ice stems from boundary friction where the temperature of the interface is still below zero, and hydrodynamic friction where the ice is melting and a thin water layer between the blade and the ice is formed. The precise value of the boundary friction coefficient is subject to ongoing research [9,10]. For example, Weber et al. [10] report friction coefficients as low as 0.01 for a 2.38 mm radius steel sphere moving on ice with velocities between  and
and 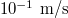 and a normal force of 1 N. However, these boundary friction values cannot be used to explain friction values in ice speed skating, where geometry, dimensions, velocities and loading are far different. Whatever the value of the boundary friction may be, we show that for typical ice speed skating conditions, its contribution to the total friction is negligible because of its extremely short contact length. This also explains why theories that do not take boundary friction into account at all work well [16,17]. Yet, we argue that boundary friction is needed for heating up the interface of the ice so that it starts to melt and hydrodynamic friction is triggered. This is actually the mechanism that allows speed skaters to almost instantaneously switch from cumbersome boundary friction at standstill to comfortable hydrodynamic friction in motion. An analytical expression for the total friction coefficient is derived. It is known that hydrodynamic friction is increased by the squeezing effect that reduces the water layer thickness between the blade and the ice. An asymptotic expression for this thickness is given as well, for large distance x. The total friction coefficient is still predicted significantly lower than that from actual speed skating measurements which is likely due to additional effects such as ice ploughing and slider blade inclination [16,17].
and a normal force of 1 N. However, these boundary friction values cannot be used to explain friction values in ice speed skating, where geometry, dimensions, velocities and loading are far different. Whatever the value of the boundary friction may be, we show that for typical ice speed skating conditions, its contribution to the total friction is negligible because of its extremely short contact length. This also explains why theories that do not take boundary friction into account at all work well [16,17]. Yet, we argue that boundary friction is needed for heating up the interface of the ice so that it starts to melt and hydrodynamic friction is triggered. This is actually the mechanism that allows speed skaters to almost instantaneously switch from cumbersome boundary friction at standstill to comfortable hydrodynamic friction in motion. An analytical expression for the total friction coefficient is derived. It is known that hydrodynamic friction is increased by the squeezing effect that reduces the water layer thickness between the blade and the ice. An asymptotic expression for this thickness is given as well, for large distance x. The total friction coefficient is still predicted significantly lower than that from actual speed skating measurements which is likely due to additional effects such as ice ploughing and slider blade inclination [16,17].